2. 中国石油集团测井有限公司测井应用研究院, 陕西 西安 710077
2. Logging Applications Institute, China Petroleum Logging Co. Ltd., Xi'an, Shaanxi 710077, China
储层渗透率是反映储集层性能好坏的重要参数,它代表储层流体在储集空间中流动的难易程度。准确评价储层渗透率对优化完井射孔方案、精细划分开发层系、制定油气田开发方案、储层地质建模及油藏数值模拟等方面具有十分重要的意义[1]。渗透率是表示流体在储集空间中渗流特征的一个参数,它的大小与岩石孔隙特征密切相关,主要取决于孔隙体积、喉道大小、孔隙喉道形状,其他因素如岩石岩相、颗粒大小分布、颗粒分选及磨圆度、胶结情况等也对渗透率有一定的影响[2-4]。长期以来一直通过测井资料建立渗透率计算方法与模型,但是没有一种测井方法可以直接获得储层渗透率。通常利用岩芯分析实验建立经验统计分析的渗透率模型,其计算结果相对误差较大[5-7];同时,该方法考虑影响因素较少,建立的模型具有区域局限性,不能有效反映储层微观结构特征对储层渗透率的影响,难以满足复杂孔隙结构渗透率评价的需求。测井新技术核磁测井拥有对储层孔隙结构评价的能力[8-12],通过岩芯刻度解释模型在渗透率评价中取得了较好的应用效果,但其昂贵的测井费用限制了在大量开发井中的应用。因此,探索一种基于常规测井资料与储层微观孔隙特征准确计算储层渗透率的方法,已成为油田高效开发对测井解释提出的迫切需求[13-14]。因此,针对砂岩储层,利用串联毛管模型从储层微观机理方面确定了储层渗透率的理论模型[15-19],建立了基于岩石物理实验的储层孔喉结构参数评价方法,实现了微观参数与宏观物理量之间的转换,为准确求取储层渗透率提供了一种新的方法。
1 串联毛管模型储层岩石孔隙结构复杂,导致相关问题难以建立相应的数学物理模型。因此,通常采用简化的物理模型来代替真实的岩石孔隙空间,例如毛管模型、逾渗模型、悬浮模型、网路模型、格子气自动机模型、孔隙喉腔节模型、颗粒增长模型、球形孔隙段节模型等。这些模型可以使研究的问题便于数学描述,但综合考虑到模型数学处理与实际储层岩石的孔喉差异性,选用串联毛管模型,如图 1a所示。
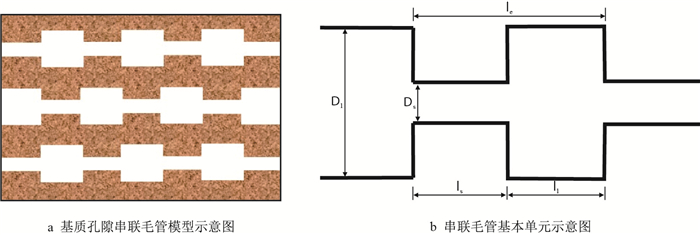 |
| 图1 串联毛管模型示意图 Fig. 1 Schematic diagram of serial capillary model |
串联毛管模型中直径较大的部分表示孔隙,直径较小的部分表示喉道,并假设所有的孔隙大小相同,所有喉道直径、长度都相等,即储层中某一深度点的岩石孔隙空间在宏观上的综合反映通过一个简化的特征模型去度量。利用串联毛管模型模拟实际岩石中,孔隙与喉道周期性交替出现,所以,可以将问题聚焦到一个基本单元对象,如图 1b所示(其中,Dl-孔隙直径,μm;Ds-喉道直径,μm;ll-孔隙长度,μm;ls-喉道长度,μm;le-基本单元的长度,μm),为串联毛管模型的一个基本单元。因此,对于具有实际物理意义的岩石宏观参数(孔隙度、渗透率、地层因素),可以通过串联毛管模型微观参数去刻画研究。
2 模型与储层宏观物理参数关系在串联毛管模型的基础上,根据岩石宏观参数的物理意义,建立毛管模型微观参数与储层宏观参数孔隙度、渗透率、地层因素之间的理论关系。首先,假设岩石的截面面积为A,岩石的长度为L,用并行排列长度为L的串联毛管束模拟岩石的孔隙结构,单位面积中有n0根串联毛管,每根串联毛管上有M个长度为le的基本单元管。利用泊稷叶方程、物质守恒及储层宏观参数物理意义,系统推导得到毛管模型微观参数与宏观物理参数之间理论关系。
毛管模型微观参数与宏观渗透率之间的关系为
| $ K = \frac{{{n_0}{\rm{ \mathsf{ π} }}{l_{\rm{e}}}D_{\rm{s}}^4}}{{128{l_{\rm{s}}}\left( {1 + \frac{{D_{\rm{s}}^4{l_{\rm{l}}}}}{{D_{\rm{l}}^4{l_{\rm{s}}}}}} \right)}} $ | (1) |
式中:K-渗透率,D;
n0-单位面积上的串联毛管数,μm-2。
毛管模型微观参数与宏观孔隙度之间的关系为
| $ ϕ =\dfrac{{{n}_{0}}MA{\rm{ \mathsf{ π} }} \left( D_{\rm s}^{2}{{l}_{\rm s}}+D_{\rm l}^{2}{{l}_{\rm l}} \right)}{4AL}=\dfrac{{{n}_{0}}{\rm{ \mathsf{ π} }} \left( D_{\rm s}^{2}{{l}_{\rm s}}+D_{\rm l}^{2}{{l}_{\rm l}} \right)}{4{{l}_{\rm e}}} $ | (2) |
式中:ϕ-孔隙度,无因次;
M-基本单元管数目,无因次;
A-岩石的截面面积,μm2;
L-岩石的长度,μm。
毛管模型微观参数与宏观地层因素之间的关系为
| $ F=\dfrac{{{R}_{\rm o}}}{{{R}_{\rm w}}}=\dfrac{4}{n{}_{0}{\rm{ \mathsf{ π} }}}\left( \dfrac{{{l}_{\rm s}}}{{{l}_{\rm e}}D_{\rm s}^{2}}+\dfrac{{{l}_{\rm l}}}{{{l}_{\rm e}}D_{\rm l}^{2}} \right) $ | (3) |
式中:F-地层因素,无因次;
Ro-孔隙中100%含水时岩石的电阻率,Ω · m;
Rw-岩石孔隙中所含水的电阻率,Ω · m。
可见,储层宏观物理参数孔隙度、渗透率、地层因素与串联毛管模型基本单元的孔隙直径、喉道直径、孔隙长度、喉道长度有关,与以往串状模型相比,增加了孔喉直径比、长度比,模型考虑更全面,更接近复杂孔隙结构储层中孔喉参数差异大的情况。
3 渗透率理论计算模型前文建立了串联毛管模型与储层宏观物理参数之间的关系式,但里面含有多个不能度量的微观模型参数,此处通过岩石物理实验建立微观参数确定方法。将模型进行简化,令δ =Dl/Ds、ls=ll,进而可以得到孔隙度、渗透率、地层因素简化的微观表达式为
| $ F=\dfrac{2}{{{n}_{0}}{\rm{ \mathsf{ π} }} }\left( \dfrac{1}{D_{\rm s}^{2}}+\dfrac{1}{D_{\rm l}^{2}} \right) $ | (4) |
| $ ϕ =\dfrac{{{n}_{0}}{\rm{ \mathsf{ π} }} \left( D_{\rm s}^{2}+D_{\rm l}^{2} \right)}{8} $ | (5) |
| $ K=\dfrac{{{n}_{0}}{\rm{ \mathsf{ π} }} D_{\rm s}^{4}}{64\left( {1+\dfrac{D_{\rm s}^{4}}{D_{\rm l}^{4}} }\right)} $ | (6) |
联立式(4)与式(5),可得
| $ \begin{array}{l} F\phi = \frac{2}{{{n_0}{\rm{\pi }}}}\left( {\frac{1}{{D_{\rm{s}}^2}} + \frac{1}{{{\delta ^2}D_{\rm{s}}^2}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\frac{{{n_0}{\rm{\pi }}\left( {D_{\rm{s}}^2 + {\delta ^2}D_{\rm{s}}^2} \right)}}{8} = \frac{{{{\left( {\delta + 1/\delta } \right)}^2}}}{4} \end{array} $ | (7) |
由式(7)可以得到孔喉直径比δ的解析方程为
| $ {{δ }^{2}}-2\sqrt{Fϕ } δ +1=0 $ | (8) |
式中:δ-孔喉直径比,无因次。
式(8)中,隐含限制条件δ >1,进而得到孔喉直径比为
| $ δ =\sqrt{Fϕ }+\sqrt{Fϕ -1} $ | (9) |
将阿尔奇公式
| $ δ =\sqrt{a{{ϕ }^{1-m}}}+\sqrt{a{{ϕ }^{1-m}}-1} $ | (10) |
式中:a-岩性系数,无因次;
m-胶结指数,无因次。
联立式(5),式(6)和式(10),可得到渗透率理论计算模型
| $ K=\dfrac{D_{\rm s}^{2}}{8\left( 1+{1}/{{{δ }^{4}}} \right)\left( 1+{{δ }^{2}} \right)} ϕ $ | (11) |
由式(1)可知,渗透率是孔隙度、孔喉直径比、喉道直径等微观参数的函数,更好地诠释了渗透率的微观物理影响因素。与常规的利用测井资料直接计算孔隙度再到渗透率相比,孔隙度前面的系数是变量,它是孔喉直径比、喉道直径的函数,由式(10)可知孔喉直径比是孔隙度与岩石导电路径复杂程度的度量[20-21],该方法从微观孔隙结构参数角度出发计算渗透率,相比孔隙度直接计算渗透率的数理回归统计更具有数学物理意义[22-24],考虑影响因素更全面。
4 模型参数确定与应用效果分析渗透率理论模型是反映微观孔隙结构的函数,测井评价的渗透率是地层某一深度点渗透率的宏观反映。因此,可以通过简化后的串联毛管模型模拟实际地层,基于理论模拟与岩石物理实验数据,得到反映某一深度宏观物理量与微观参数的转换关系,实现渗透率的准确计算。
孔隙度可由孔隙度测井曲线计算得到[25-26],通过研究区岩芯分析资料刻度测井资料,建立孔隙度计算模型
| $ ϕ =-0.6135 ρ+ 1.6145 $ | (12) |
式中:ρ-测井密度,g/cm3。
利用研究区岩电实验建立孔隙度与地层因素关系(图 2)[27],确定储层岩电参数a=0.918 2,m=1.753 2,通过式(10)可以获得测井连续计算的孔喉直径比参数。
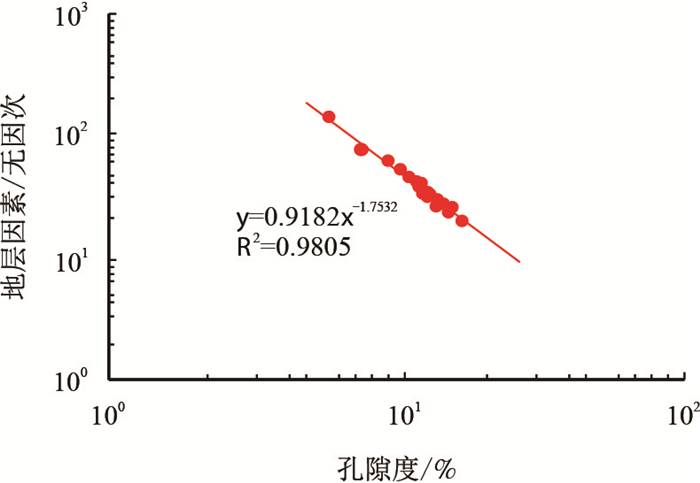 |
| 图2 孔隙度与地层因素关系 Fig. 2 Relationship between porosity and formation factors |
储层喉道直径的主要影响因素有两个:一是孔隙度反映储层整体储集空间的大小,孔隙度越大一般对应的喉道直径也越大;另一个是储层砂岩粒度与泥质含量,粒度越小喉道直径越小,泥质含量越重孔隙结构越复杂,对应的喉道直径也越小。这两个影响因素可以通过自然伽马曲线来度量,一般需要对自然伽马曲线进行归一化,引入自然伽马曲线相对值,如式(13)所示
| $ Δ G_{\rm R}=\dfrac{G_{\rm R}-G_{{\rm R}_{\rm min}}}{G_{{\rm R}_{\rm max}}-G_{{\rm R}_{\rm min}}} $ | (13) |
式中:ΔGR-自然伽马相对值,无因次;
GR-自然伽马测量值,API;
GRmin-纯砂岩自然伽马测量值,API;
GRmax-纯泥岩段自然伽马测量值,API。
在物性分析数据与岩电实验数据的基础上,结合式(10),式(11)可以得到物性实验岩芯对应的喉道直径。将计算的岩芯喉道直径与孔隙度、自然伽马相对值分别建立相关性分析,如图 3所示。从图中可以看出,喉道直径与孔隙度、自然伽马相对值有很好的相关性。因此,构建喉道直径计算模型为
| $ {{D}_{\rm s}}=Aϕ +B\ln Δ G_{\rm R}+C $ | (14) |
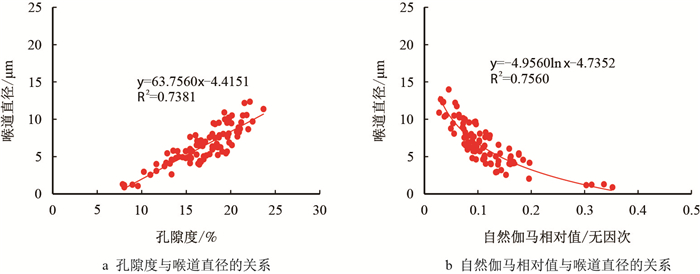 |
| 图3 孔隙度、自然伽马相对值与喉道直径的关系 Fig. 3 Relationship between throat diameter and porosity, natural gamma relative value |
式中:A,B,C-回归系数,无因次。
通过多元回归,可确定式(14)中的系数:A=39.723 8,B=-2.496 1,C=-6.103 4。利用测井资料可以连续计算孔隙度与自然伽马相对值,通过式(14)得到储层中不同位置的喉道直径。在此基础上,利用式(11)可计算出研究区储层中不同深度点处渗透率值。
渗透率计算结果如图 4所示。从图 4可以看出,孔隙度、渗透率计算结果与岩芯分析结果一致性较好,能够较好地反映渗透率在纵向上随储层特性的变化规律。
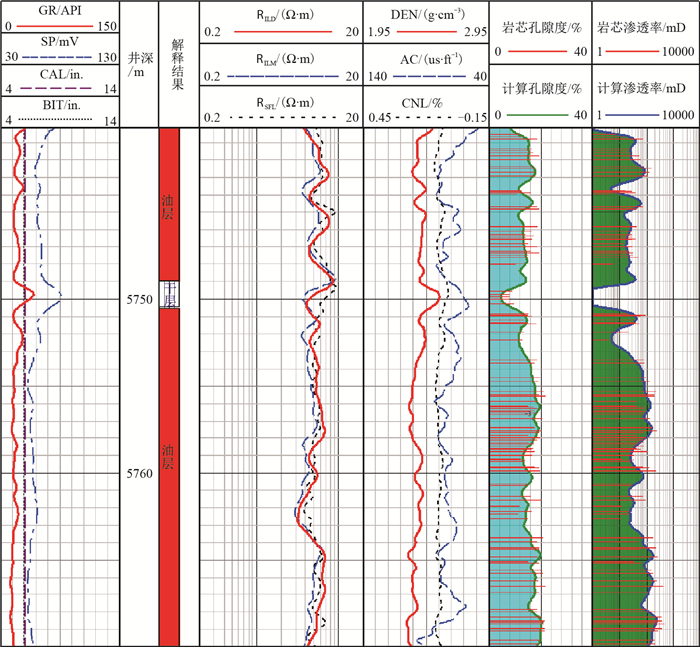 |
| 图4 渗透率计算结果图 Fig. 4 Permeability calculation results |
将岩芯分析渗透率与计算渗透率进行对比分析,如图 5所示,两者稳定分布在45°对角线附近,两者计算结果一致性好。本方法实现了渗透率的高精度计算,从储层微观机理中明确了储层渗透率的影响因素,建立了储层微观结构参数与宏观渗透率的理论表征方法。
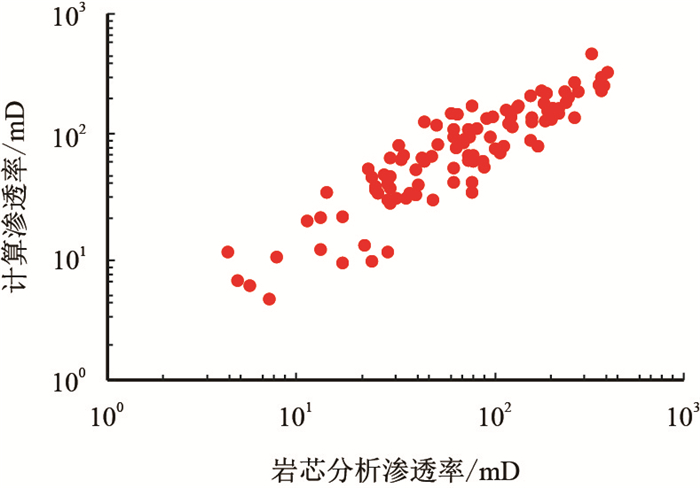 |
| 图5 岩芯渗透率与计算渗透率对比 Fig. 5 Comparison between core permeability and calculated permeability |
(1) 串联毛管模型可以有效表征储层孔喉结构的差异,基于该模型建立微观孔隙结构参数与储层宏观物理量孔隙度、渗透率、地层因素理论关系,实现了宏观物理量的微观表征。
(2) 在微观孔隙结构参数与储层宏观物理量的理论关系上,创新性地引入岩电实验地层因素,首次确定了孔喉直径比的解析方程式。
(3) 渗透率的理论模型表明,储层宏观渗透率是孔隙度、孔喉直径比、喉道直径等微观参数的函数,明确了渗透率的微观物理影响因素。
(4) 利用渗透率理论模型计算的渗透率与岩芯分析渗透率计算结果一致性较好,为储层渗透率计算提供了一种基于微观参数的计算方法,对于孔隙结构复杂的储层具有广阔的应用前景。
| [1] |
王晓畅, 范宜仁, 邓少贵. 复杂砂岩储层基于相控建模的渗透率计算方法[J]. 物探化探计算技术, 2008, 30(6): 487-489. WANG Xiaochang, FAN Yiren, DENG Shaogui. Method of permeability model of complicated sand reservoirs based on facies-controlled modeling[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(6): 487-489. doi: 10.3969/j.issn.1001-1749.2008.06.008 |
| [2] |
李显路, 刘芳, 西涛涛, 等. 安棚地区Ⅳ油组渗透率计算方法研究[J]. 石油天然气学报, 2011, 33(11): 10. LI Xianlu, LIU Fang, XI Taotao, et al. Computation of permeability of Ⅳ oil group in Anpeng Area[J]. Journal of Oil and Gas Technology, 2011, 33(11): 10. doi: 10.3969/j.issn.1000-9752.2011.11.022 |
| [3] |
田虓丰, 程林松, 李翔龙, 等. 考虑微观孔喉结构的相对渗透率计算方法[J]. 陕西科技大学学报, 2014, 32(6): 10. TIAN Xiaofeng, CHENG Linsong, LI Xianglong, et al. A new method to calculate relative permeability considering the effect of pore-throat distribution[J]. Journal of Shaanxi University of Science & Technology, 2014, 32(6): 10. doi: 10.3969/j.issn.1000-5811.2014.06.022 |
| [4] |
李奇, 高树生, 刘华勋, 等. 岩心渗透率的精确计算方法及其适用范围实验研究[J]. 西安石油大学学报(自然科学版), 2015, 30(2): 69-74. LI Qi, GAO Shusheng, LIU Huaxun, et al. Experimental study on accurate calculation method of core permeability and applicable scope[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2015, 30(2): 69-74. doi: 10.3969/j.issn.1673-064X.2015.02.013 |
| [5] |
荆万学. 常规测井资料计算砂岩储层渗透率的理论思考[J]. 测井技术, 2002, 26(1): 46-48. JING Wanxue. A theoretical method for calculation of sandstone reservoir with conventional logging data[J]. Well Logging Technology, 2002, 26(1): 46-48. doi: 10.3969/j.issn.1004-1338.2002.01.011 |
| [6] |
李文湘, 王培春, 吕洪志, 等. 基于PICKETT交会图油气层渗透率计算方法研究[J]. 测井技术, 2013, 37(4): 385-388. LI Wenxiang, WANG Peichun, LÜ Hongzhi, et al. On calculation method of hydrocarbon reservoir permeability based on PICKETT crossplot[J]. Well Logging Technology, 2013, 37(4): 385-388. doi: 10.3969/j.issn.1004-1338.2013.04.009 |
| [7] |
杨兴旺, 赵杰, 朱友青. 利用孔隙分类法计算火成岩储层渗透率的方法及其应用[J]. 测井技术, 2010, 34(2): 164-167. YANG Xingwang, ZHAO Jie, ZHU Youqing. A P3A method to calculate volcanic reservoir permeability and its application[J]. Well Logging Technology, 2010, 34(2): 164-167. doi: 10.3969/j.issn.1004-1338.2010.02.014 |
| [8] |
邵维志, 解经宇, 迟秀荣, 等. 低孔隙度低渗透率岩石孔隙度与渗透率关系研究[J]. 测井技术, 2013, 37(2): 149-153. SHAO Weizhi, XIE Jingyu, CHI Xiurong, et al. On the relation of porosity and permeability in low porosity and low permeability rock[J]. Well Logging Technology, 2013, 37(2): 149-153. doi: 10.3969/j.issn.1004-1338.2013.02.007 |
| [9] |
肖忠祥, 肖亮. 基于核磁共振测井和毛管压力的储层渗透率计算方法[J]. 原子能科学技术, 2008, 42(10): 868-871. XIAO Zhongxiang, XIAO Liang. Method of calculate reservoir permeability using nuclear magnetic resonance logging and capillary pressure data[J]. Atomic Energy Science and Technology, 2008, 42(10): 868-871. |
| [10] |
周明顺, 殷洁, 潘景丽, 等. 基于核磁共振测井孔喉的低渗透储层有效性评价方法[J]. 测井技术, 2014, 38(4): 452-457. ZHOU Mingshun, YIN Jie, PAN Jingli, et al. Method for effectiveness evaluation of low permeability reservoir based on NMR logging pore[J]. Well Logging Technology, 2014, 38(4): 452-457. doi: 10.3969/j.issn.1004-1338.2014.04.014 |
| [11] |
孙海, 姚军, 张磊, 等. 基于孔隙结构的页岩渗透率计算方法[J]. 中国石油大学学报(自然科学版), 2014, 38(2): 92-98. SUN Hai, YAO Jun, ZHANG Lei, et al. A computing method of shale permeability based on pore structures[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014, 38(2): 92-98. doi: 10.3969/j.issn.1673-5005.2014.02.014 |
| [12] |
王天娇, 范小伟, 王天雨, 等. 基于碎屑岩孔隙结构特征参数的渗透率计算方法研究[J]. 长江大学学报(自科版), 2014, 11(14): 13-15. WANG Tianjiao, FAN Xiaowei, WANG Tianyu, et al. On calculation method of permeability based on clastic characteristic parameters of pore structure[J]. Journal of Yangtze University (Natural Science Edition), 2014, 11(14): 13-15. |
| [13] |
贾文玉, 闫安宇, 田素月. 渗透率的理论计算方法[J]. 测井技术, 2000, 24(3): 216-219. JIA Wenyu, YAN Anyu, TIAN Suyue. Theoretical calculation method of permeability[J]. Well Logging Technology, 2000, 24(3): 216-219. doi: 10.3969/j.issn.1004-1338.2000.03.013 |
| [14] |
张吉昌, 刘月田, 丁燕飞, 等. 裂缝各向异性油藏孔隙度和渗透率计算方法[J]. 中国石油大学学报(自然科学版), 2006, 30(5): 62-66. ZHANG Jichang, LIU Yuetian, DING Yanfei, et al. Calculation method of porosity and permeability in fractured anisotropic oil reservoirs[J]. Journal of China University of Petroleum (Edition of Natural Science), 2006, 30(5): 62-66. doi: 10.3321/j.issn:1000-5870.2006.05.015 |
| [15] |
关继腾, 于华, 王谦, 等. 储层岩石时间域激发极化效应的数学模拟[J]. 计算物理, 2012, 29(3): 354-360. GUAN Jiteng, YU Hua, WANG Qian, et al. Mathematical simulation on induced polarization of reservoir rock in time domain[J]. Chinese Journal of Computational Physics, 2012, 29(3): 354-360. doi: 10.3969/j.issn.1001-246X.2012.03.006 |
| [16] |
关继腾, 王谦, 范业活, 等. 利用毛管模型研究泥质砂岩电化学测井响应机理[J]. 地球物理学报, 2010, 53(1): 214-223. GUAN Jiteng, WANG Qian, FAN Yehuo, et al. Stuy on the mechanisms of electrochemical logging response in shaly sandstone based on capillary model[J]. Chinese Journal of Geophysics, 2010, 53(1): 214-223. doi: 10.3969/j.issn.0001-5733.2010.01.024 |
| [17] |
王谦, 关继腾, 房文静. 泥质砂岩激发极化弛豫时间谱微观机理[J]. 煤田地质与勘探, 2010, 38(3): 61-65. WANG Qian, GUAN Jiteng, FANG Wenjing. The microscopic mechanisms of induced polarization relaxation time spectra in shaly sandstone[J]. Coal Geology & Exploration, 2010, 38(3): 61-65. doi: 10.3969/j.issn.1001-1986.2010.03.014 |
| [18] |
于华, 关继腾, 陈辉, 等. 储层岩石流动电位频散特性的数学模拟[J]. 地球物理学报, 2013, 56(2): 676-687. YU Hua, GUAN Jiteng, CHEN Hui, et al. Mathematical simulation on the frequency dispersion characteristics of the streaming potential in reservoir rocks[J]. Chinese Journal of Geophysics, 2013, 56(2): 676-687. doi: 10.6038/cjg20130232 |
| [19] |
关继腾, 程媛媛, 于华. 利用等效电路模型研究泥质砂岩复电阻率频散特性[J]. 测井技术, 2011, 35(6): 512-517. GUAN Jiteng, CHENG Yuanyuan, YU Hua. On the frequency dispersion characteristics of complex resistivity in shaly sandstone based on equivalent circuit model[J]. Well Logging Technology, 2011, 35(6): 512-517. doi: 10.3969/j.issn.1004-1338.2011.06.004 |
| [20] |
张龙海, 周灿灿, 刘国强, 等. 孔隙结构对低孔低渗储集层电性及测井解释评价的影响[J]. 石油勘探与开发, 2006, 33(6): 671-676. ZHANG Longhai, ZHOU Cancan, LIU Guoqiang, et al. Influence of pore structures on electric properties and well logging evaluation in low porosity and permeability reservoirs[J]. Petroleum Exploration and Development, 2006, 33(6): 671-676. doi: 10.3321/j.issn:1000-0747.2006.06.006 |
| [21] |
韩双, 潘保芝. 孔隙储层胶结指数m的确定方法及影响因素[J]. 油气地球物理, 2010, 8(1): 43-47. HAN Shuang, PAN Baozhi. Determination methods and influencing factors of the bond index m of the complex reservoir[J]. Petroleum Geophysics, 2010, 8(1): 43-47. |
| [22] |
魏兴华. 砂岩储层渗透率表征方法探讨[J]. 断块油气田, 2006, 13(3): 16-17. WEI Xinghua. A new method for calculating permeability of sandstone reservoir[J]. Fault-Block Oil & Gas Field, 2006, 13(3): 16-17. doi: 10.3969/j.issn.1005-8907.2006.03.005 |
| [23] |
谢伟彪, 周凤鸣, 司兆伟, 等. 基于数理推导的砂岩地层渗透率计算新模型[J]. 测井技术, 2014, 38(5): 553-557. XIE Weibiao, ZHOU Fengming, SI Zhaowei, et al. New calculation model of permeability in sandstone formation by the mathematical derivation[J]. Well Logging Technology, 2014, 38(5): 553-557. doi: 10.3969/j.issn.1004-1338.2014.05.010 |
| [24] |
刘向君, 夏宏泉, 赵正文. 砂泥岩地层渗透率预测通用计算模型[J]. 西南石油学院学报, 1999, 21(1): 10-12. LIU Xiangjun, XIA Hongquan, ZHAO Zhengwen. Establishing a general model of permeability for sand-shale formations[J]. Journal of Southwest Petroleum Institute, 1999, 21(1): 10-12. doi: 10.3863/j.issn.1674-5086.1999.01.003 |
| [25] |
邱隆伟, 师政, 付大巍, 等. 临南洼陷沙三段孔隙度控制因素分析与定量模型[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1321-1331. QIU Longwei, SHI Zheng, FU Dawei, et al. Controlling factors analysis and quantitative model of Shahejie 3rd sandstone porosity in Linnan Sag[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1321-1331. doi: 10.13278/j.cnki.jjuese.201605105 |
| [26] |
王鹏. 泌阳凹陷孙岗地区储层测井解释方法研究[J]. 石油地质与工程, 2007, 21(1): 31-33. WANG Peng. A study of logging interpretation methods in Sungang areas in Biyang Sag[J]. Petroleum Geology and Engineering, 2007, 21(1): 31-33. doi: 10.3969/j.issn.1673-8217.2007.01.010 |
| [27] |
张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究[J]. 石油物探, 2005, 44(1): 21-23, 28. ZHANG Minglu, SHI Yujiang. Archie's electrical parameters of complex pore texture in sandstone reservoir[J]. Geophysical Prospecting for Petroleum, 2005, 44(1): 21-23, 28. doi: 10.3969/j.issn.1000-1441.2005.01.006 |
 2020, Vol. 42
2020, Vol. 42


