2. 四川长宁天然气开发有限责任公司, 四川 成都 610500;
3. 重庆科技学院石油与天然气工程学院, 重庆 沙坪坝 401331
2. Sichuan Changning Natural Gas Development Co. Ltd., Chengdu, Sichuan 610500, China;
3. School of Petroleum Engineering, Chongqing University of Science & Technology, Shapingba, Chongqing 401331, China
页岩气藏作为重要的非常规气藏之一,通常具有超低孔、超低渗等特征,其中,孔隙度多低于10%,基质渗透率在纳达西级,此外,储层内还发育有天然微裂缝。页岩气主要以游离气、吸附气和少量溶解气储存于地下,其中,游离气多聚集在天然裂缝和基质孔隙之中,吸附气赋存于基质表面,而溶解气存在于干酪根和沥青质中,占比十分微小,可忽略不计[1-3]。通常对上述3种气体描述均指原始状态下的特征,因此,理论研究中的解吸气应为吸附气的一部分,而非游离气。不同于常规气藏,页岩气藏中存在大量的吸附气,在页岩气藏储量评价[4-5]及渗流理论[6-7]研究中均不可忽视,游离气与吸附气在气藏开发中的变化规律对气藏开发显得尤为重要。然而,吸附气在降压解吸时受多种因素影响[8-10],解吸出的气体与游离气共同流动,由于解吸量较难确定,导致难以准确地获取页岩含气量变化特征。
页岩含气量测定方法有测井解释法、现场解吸法及室内等温吸附实验法。测井解释法首先需要分别基于等温吸附实验和岩石物理实验,建立吸附气与有机碳含量(TOC)关系、游离气与含气饱和度、岩石密度和有效孔隙度关系,然后利用测井解释数据获取相关储层物性参数,进而计算两种气体含量[11-12],故测井解释的合理性十分关键。现场解吸法是将岩芯放入解吸罐后在大气压力下自然解吸出的气体含量[3],这种方法无法较好地区分游离气和吸附气,同时在装岩芯过程中还会产生损失气[13],难以准确测量。室内等温吸附实验法是在较为严格的条件下完成的,可进行页岩气吸附[14-18]与解吸[7-9, 19]的特征分析,但目前尚未应用于游离气特征分析。由于测井解释法、现场解吸法主要应用于现场,受环境、设备以及人为因素的影响较大,两种方法的测试精度及操作简便性远不如室内等温吸附实验法,若能基于室内等温吸附实验法进一步明确游离气变化特征,则对准确认识页岩气藏开发中各赋存气变化规律具有重要意义。因此,本文基于容积法的页岩气等温吸附实验建立了相应的物理模型及数学模型,并结合实测数据验证了模型的可行性,该模型能够有效地揭示页岩含气量的变化特征。
1 页岩样品物理模型的建立 1.1 等径颗粒排列基于容积法的页岩气等温吸附实验样品粉末粒径为0.150
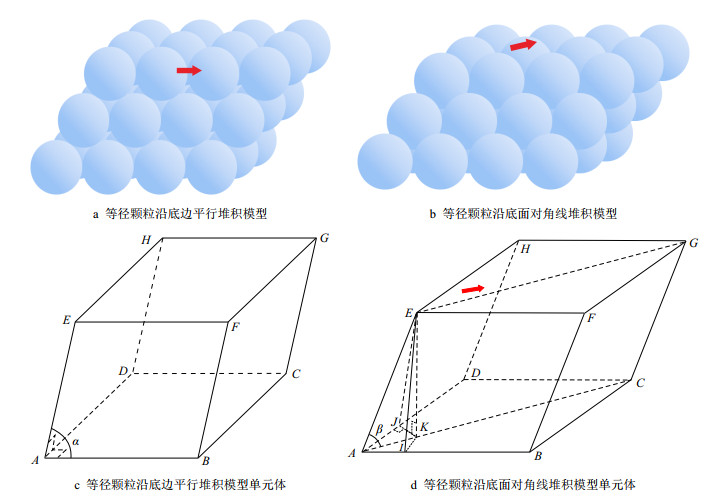 |
| 图1 等径球形颗粒堆积示意图 Fig. 1 Isodiametric spherical particle packing patterns |
由图 1a、图 1c可知,当斜面与底面的夹角为
| $ {\phi _{\rm{ \mathit{ α} }}}\!=\!\dfrac{{V_{{\rm{total}}}^{\rm{ \mathit{ α} }}{\rm{\!-\!}}{V_{{\rm{sphere}}}}}}{{V_{{\rm{total}}}^{\rm{ \mathit{ α} }}}}\!\times\!100{\rm{\% }}\!=\!\left( {1\!-\!\dfrac{{\rm{ \mathsf{ π} }}}{6}\sin \alpha } \right)\!\times\!100{\rm{\% }} $ | (1) |
式中:
在[60°,90°]区间,sin
由图 1b、图 1d可知,当斜棱边与底面夹角为
| $ {\phi _{\rm{ \mathit{ β} }}}\!=\!\dfrac{{V_{{\rm{total}}}^{\rm{ \mathit{ β} }}{\rm{\!-\!}}{V_{{\rm{sphere}}}}}}{{V_{{\rm{total}}}^{\rm{ \mathit{ β} }}}} \times 100{\rm{\% }}\!=\! \\ \; \; \; \;\left[\!{1\!-\!\dfrac{{\rm{ \mathsf{ π} }}}{{6\left( {1\!-\!\cos \beta } \right)\sqrt {1\!+\!2\cos \beta } }}} \right]\!\times\!100{\rm{\% }} $ | (2) |
式中:
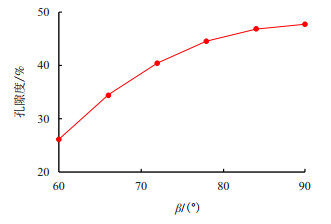
有图 2可知,在[60°,90°]区间,
 |
|
图2
孔隙度随 |
等径颗粒不同排列方式下的孔隙度为25.95%
由此可知,孔隙度与颗粒堆积方式及填充程度有关,与颗粒粒径大小无关。根据实验原理中的最小粒径与最大粒径比约为0.353,介于2次球(0.414)与3次球(0.225)可知,样品颗粒骨架孔隙度应分布在19.00%
页岩气分子受页岩孔壁势能作用而吸附于其中,描述页岩气吸附的理论模型较多[28],其中,式(3)所示基于吸附气密度修正后的Langmuir方程,因其形式简洁,物理意义明确而被广泛应用。
| $ {V_{{\rm{ad}}}} = {V_{\rm{L}}}\dfrac{p}{{p + {p_{\rm{L}}}}}\left( {1 - \dfrac{{{\rho _{\rm{f}}}}}{{{\rho _{{\rm{ad}}}}}}} \right) $ | (3) |
对式(3)进行标准状态(0 ℃,101.325 kPa)校正可得
| $ V_{{\rm{ad}}}^{{\rm{sc}}} = {V_{\rm{L}}}\dfrac{p}{{p + {p_{\rm{L}}}}}\left( {1 - \dfrac{{{\rho _{\rm{f}}}}}{{{\rho _{{\rm{ad}}}}}}} \right) \times 22.4 \times 1000 $ | (4) |
式中:
通过测量岩样装入吸附罐后空间体积减少量,可确定岩样外表体积
| $ {V_{{\rm{app}}}} = {V_{{\rm{bf}}}} - {V_{{\rm{af}}}} $ | (5) |
式中:
由于测试压力下岩样被压实,此时岩样体积为
| $ {V_{\rm{R}}} = {V_{{\rm{app}}}} - {c_{\rm{f}}}p{V_{{\rm{app}}}} $ | (6) |
式中:
其中,岩样压缩系数可由固体骨架压缩系数确定[29]
| $ {c_{\rm{s}}} = \dfrac{{3\left( {1 - 2\nu } \right)}}{{{E_{\rm{s}}}}} $ | (7) |
| $ {c_{\rm{f}}} = \dfrac{\phi }{{1 - \phi }}{c_{\rm{s}}} $ | (8) |
式中:
由式(5)
| $ {V_{\rm{f}}}\!=\!\phi {V_{\rm{R}}}\!=\!\phi \left( {{V_{{\rm{bf}}}}\!-\! {V_{{\rm{af}}}}} \right)\left[ {1\!-\!\dfrac{\phi }{{1\!-\!\phi }}\dfrac{{3\left( {1\!-\!2\nu } \right)}}{{{E_{\rm{s}}}}}p} \right] $ | (9) |
式中:
利用气体状态方程可获得测试温度、压力下自由空间内页岩单位质量下的游离气体积,并进行标准状态校正,即
| $ V_{\rm{g}}^{{\rm{sc}}} = \dfrac{{p{V_{\rm{f}}}}}{{{m_{\rm{s}}}Z{\rm{R}}T}} \times 22.4 \times 1000 $ | (10) |
式中:
R—气体常数,R=8.3144 J/(mol
联立式(9)和式(10),可得标准状态时单位页岩质量下游离气体积为
| $ V_{\rm{g}}^{{\rm{sc}}} = \dfrac{{p\phi \left( {{V_{{\rm{bf}}}} - {V_{{\rm{af}}}}} \right)}}{{{m_{\rm{s}}}ZT{\rm{R}}}}\left[ {1 - \dfrac{\phi }{{1 - \phi }}\dfrac{{3\left( {1 - 2\nu } \right)}}{{{E_{\rm{s}}}}}p} \right] \times \\ \; \; \; \; \; 22.4 \times 1000 $ | (11) |
由此可建立吸附气量与游离气量比例关系式
| $ \omega _{{\rm{ad}}}^{{\rm{sc}}} = \dfrac{{V_{{\rm{ad}}}^{{\rm{sc}}}}}{{V_{{\rm{ad}}}^{{\rm{sc}}} + V_{\rm{g}}^{{\rm{sc}}}}} $ | (12) |
| $ \omega _{\rm{g}}^{{\rm{sc}}} = 1 - \omega _{{\rm{ad}}}^{{\rm{sc}}} $ | (13) |
式中:
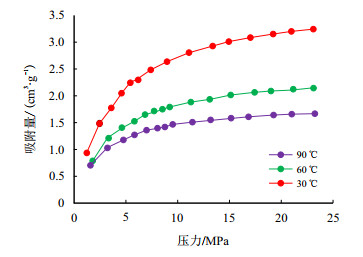
选取重庆某区域页岩样品,采用容积法开展了页岩气等温吸附实验的测试。该实验通过测试吸附罐内测试压力与平衡压力间罐内气体的改变量来获取样品的吸附量,其中,实验测试温度分别为30,60,90 ℃,测试压力为1
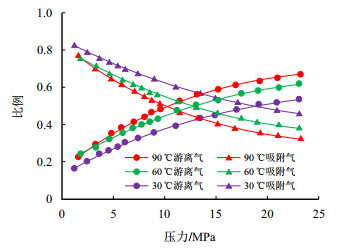
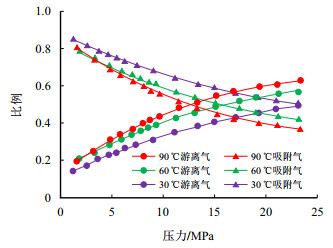
基于1.2节的分析结果,假定样品孔隙度依次为5.37%,4.93%,4.10%等3种情况,利用建立的吸附气与游离气比例关系式,结合页岩气等温吸附实验结果,可得不同温度、压力下3种情况的页岩含气量占比关系(图 4
 |
|
图4
|
 |
|
图5
|
 |
|
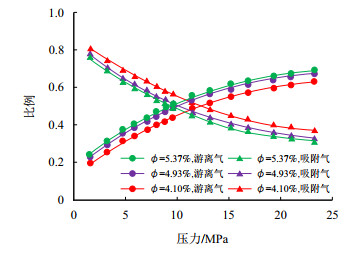
图6
|
 |
| 图7 90 ℃时各孔隙度下的吸附气与游离气比例关系图 Fig. 7 Relationship between adsorption gas and free gas under different porosity at 90 ℃ |
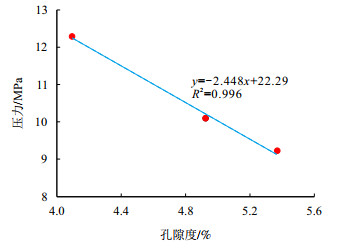 |
| 图8 90 ℃下吸附气与游离气占比相等时的压力与孔隙度关系图 Fig. 8 Relationship between pressure and porosity when the proportion of adsorbed gas and free gas is equal at 90 ℃ |
| 表2 不同孔隙度在各温度、压力下的吸附气与游离气比例统计表 Tab. 2 Proportions of adsorbed gas and free gas at different temperatures, pressures and porosity |
对上述实验数据及处理结果分析可知:
(1) 随着压力的下降,吸附气量下降,而其占比上升,降幅和增幅均先慢后快,变化拐点约在10 MPa。90 ℃下当压力由23 MPa降至10 MPa时,孔隙度为5.37%,4.93%,4.10%时吸附气占比在单位压差下的升幅依次为4.23%/MPa,4.05%/MPa和3.68%/MPa,10 MPa降至5 MPa时则为5.95%/MPa,5.64%/MPa和4.99%/MPa。表明高压时孔隙内储存大量压缩的游离气,降压初期由于游离气更易流动而优先逸出,当压力降至约10 MPa时孔隙内剩余游离气量较少,吸附气占比逐渐升高。
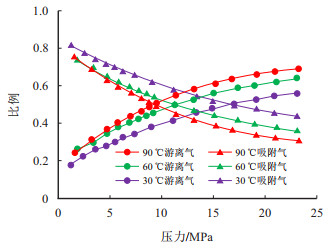
(2) 随着温度的增加,游离气比例逐渐增加。由图 4
(3) 孔隙度对页岩气赋存状态具有较大影响,孔隙度越小,游离气占比越小。由图 7和表 2可知,90 ℃下23 MPa时,游离气占比在
(4) 页岩气藏多为高温高压状态,在开发时储层温度变化不大而压力下降显著,此时对孔道内主要流动气体(游离气与解吸气)组成影响较大。图 9为90 ℃下
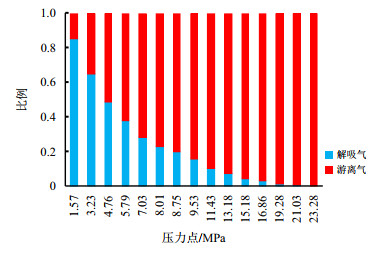 |
| 图9 解吸气与游离气比例变化图 Fig. 9 Variation of proportions the desorption gas to free gas |
(1) 利用Horsfield填充理论建立了基于容积法的页岩气等温吸附实验的物理模型,提出了能够快速定量表征页岩含气量变化的新方法,结合实例分析验证了新方法的可行性。
(2) 页岩气藏开发时储层温度通常变化较小而压力下降显著,使得孔道内的气体组成从以游离气为主转变为以解吸气为主,即主要气源从游离气转向为吸附气,并且转折点所对应的压力与孔隙度呈负线性相关。
| [1] |
LI Jing, ZHOU Shixin, GAUS G, et al. Characterization of methane adsorption on shale and isolated kerogen from the Sichuan Basin under pressure up to 60 MPa:Experimental results and geological implications[J]. International Journal of Coal Geology, 2018, 189: 83-93. doi: 10.1016/j.coal.2018.02.020 |
| [2] |
ZHANG Liehui, CHEN Zhangxin, ZHAO Yulong. Well production performance analysis for shale gas reservoirs[M]. Amsterdam: Elsevier, 2018: 2-39.
|
| [3] |
唐颖, 张金川, 刘珠江, 等. 解吸法测量页岩含气量及其方法的改进[J]. 天然气工业, 2011, 31(10): 108-112. TANG Ying, ZHANG Jinchuan, LIU Zhujiang, et al. Use and improvement of the desorption method in shale gas content tests[J]. Natural Gas Industry, 2011, 31(10): 108-112. doi: 10.3787/j.issn.1000-0976.2011.10.026 |
| [4] |
JIANG Wenbin, LIN Mian. Molecular dynamics investigation of conversion methods for excess adsorption amount of shale gas[J]. Journal of Natural Gas Science and Engineering, 2018, 49: 241-249. doi: 10.1016/j.jngse.2017.11.006 |
| [5] |
ZHOU Shangwen, XUE Huaqing, NING Yang, et al. Experimental study of supercritical methane adsorption in Longmaxi shale:Insights into the density of adsorbed methane[J]. Fuel, 2018, 211: 140-148. doi: 10.1016/j.fuel.2017.09.065 |
| [6] |
WANG Jing, LUO Haishan, LIU Huiqing, et al. An integrative model to simulate gas transport and production coupled with gas adsorption, non-Darcy flow, surface diffusion, and stress dependence in organic-shale reservoirs[J]. SPE Journal, 2017, 22(1): 244-264. doi: 10.2118/174996-PA |
| [7] |
ZHANG Liehui, LIANG Hongbin, ZHAO Yulong, et al. Gas transport characteristics in shale matrix based on multiple mechanisms[J]. Chemical Engineering Journal, 2020, 386: 124002. doi: 10.1016/j.cej.2019.124002 |
| [8] |
关富佳, 张杰, 王海涛, 等. 川东龙马溪组页岩解吸滞后现象实验研究[J]. 西安石油大学学报(自然科学版), 2017, 32(1): 71-74, 82. GUAN Fujia, ZHANG Jie, WANG Haitao, et al. Experimental study on desorption hysteresis of Longmaxi Formation shale in eastern Sichuan[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2017, 32(1): 71-74, 82. doi: 10.3969/j.issn.1673-064X.2017.01.011 |
| [9] |
刘勇, 唐善法, 姚逸风, 等. 页岩气超临界吸附与解吸附特性及影响因素[J]. 大庆石油地质与开发, 2015, 34(2): 170-174. LIU Yong, TANG Shanfa, YAO Yifeng, et al. Supercritical adsorption and desorption characteristics and influencing factors for the shale gas[J]. Petroleum Geology and Oilfield Development in Daqing, 2015, 34(2): 170-174. doi: 10.3969/J.ISSN.1000-3754.2015.02.034 |
| [10] |
马东民, 曹石榴, 李萍, 等. 页岩气与煤层气吸附/解吸热力学特征对比[J]. 煤炭科学技术, 2015, 43(2): 64-67. MA Dongmin, CAO Shiliu, LI Ping, et al. Comparison on adsorption and desorption thermodynamics features between shale gas and coalbed methane[J]. Coal Science and Technology, 2015, 43(2): 64-67. doi: 10.13199/j.cnki.cst.2015.02.014 |
| [11] |
史鹏, 姜呈馥, 陈义国, 等. 鄂尔多斯盆地延长组页岩含气量测井评价[J]. 特种油气藏, 2016, 23(3): 61-65. SHI Peng, JIANG Chengfu, CHEN Yiguo, et al. Logging evaluation of Yanchang Shale Gas content in Ordos Basin[J]. Special Oil and Gas Reservoirs, 2016, 23(3): 61-65. doi: 10.3969/j.issn.1006-6535.2016.03.014 |
| [12] |
钟光海, 谢冰, 周肖, 等. 四川盆地页岩气储层含气量的测井评价方法[J]. 天然气工业, 2016, 36(8): 43-51. ZHONG Guanghai, XIE Bing, ZHOU Xiao, et al. A logging evaluation method for gas content of shale gas reservoirs in the Sichuan Basin[J]. Natural Gas Industry, 2016, 36(8): 43-51. doi: 10.3787/j.issn.1000-0976.2016.08.006 |
| [13] |
淮银超, 曲良超, 张铭, 等. 基于测井资料的页岩含气量评价方法[J]. 科学技术与工程, 2017, 17(29): 33-38. HUAI Yinchao, QU Liangchao, ZHANG Ming, et al. Evaluation method of shale gas content based on logging data[J]. Science Technology and Engineering, 2017, 17(29): 33-38. doi: 10.3969/j.issn.1671-1815.2017.29.005 |
| [14] |
LI Jianchao, ZHANG Liehui, CHEN Yulin. Adsorption behavior study of shale gas: models and new combination approach[C]. SPE 176880-MS, 2015. doi: 10.2118/176880-MS
|
| [15] |
YANG Sheng, WU Wei, XU Jinze, et al. Volume effects on methane-shale adsorption under reservoir conditions[C]. SPE 180076-MS, 2016. doi: 10.2118/180076-MS
|
| [16] |
李希建, 李维维, 黄海帆, 等. 深部页岩高温高压吸附特性分析[J]. 特种油气藏, 2017, 24(3): 129-134. LI Xijian, LI Weiwei, HUANG Haifan, et al. Analysis on adsorption characteristics of deep shale under high temperature and high pressure[J]. Special Oil and Gas Reservoirs, 2017, 24(3): 129-134. doi: 10.3969/j.issn.1006-6535.2017.03.025 |
| [17] |
SANDER R, PAN Zhejun, LUKE D C, et al. Controls on methane sorption capacity of Mesoproterozoic gas shales from the Beetaloo Sub-basin, Australia and global shales[J]. International Journal of Coal Geology, 2018, 199: 65-90. doi: 10.1016/j.coal.2018.09.018 |
| [18] |
马斌玉, 徐守余, 陈麦雨, 等. 页岩的甲烷吸附能力影响因素综述[J]. 海相油气地质, 2018, 23(2): 31-38. MA Binyu, XU Shouyu, CHEN Maiyu, et al. An overview of influence factors of methane adsorption capacity in shale[J]. Marine Origin Petroleum Geology, 2018, 23(2): 31-38. doi: 10.3969/j.issn.1672-9854.2018.02.005 |
| [19] |
郭为, 熊伟, 高树生, 等. 页岩气等温吸附/解吸特征[J]. 中南大学学报(自然科学版), 2013, 44(7): 2836-2840. GUO Wei, XIONG Wei, GAO Shusheng, et al. Isothermal adsorption/desorption characteristics of shale gas[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2836-2840. |
| [20] |
中国国家标准化管理委员会. GB/T 35210..2017页岩甲烷等温吸附测定方法第1部分: 容积法[S].北京: 中国标准出版社, 2017.
|
| [21] |
中国国家标准化管理委员会. GB/T 1956.2008煤的高压等温吸附试验方法[S].北京: 中国标准出版社, 2008.
|
| [22] |
国家能源局. SY/T 613.2013煤岩中甲烷等温吸附量测定干燥基容量法[S].北京: 石油工业出版社, 2014.
|
| [23] |
李爱芬. 油层物理学[M]. 3版. 东营: 中国石油大学出版社, 2011: 148-149. LI Aifen. Petrophysics[M]. 3rd ed. Dongying: China University of Petroleum press, 2011: 148-149. |
| [24] |
邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景(一)[J]. 石油勘探与开发, 2015, 42(6): 689-701. ZOU Caineng, DONG Dazhong, WANG Yuman, et al. Shale gas in China:Characteristics, challenges and prospects (Ⅰ)[J]. Petroleum Exploration and Development, 2015, 42(6): 689-701. doi: 10.11698/PED.2015.06.01 |
| [25] |
陆厚根. 粉体工程导论[M]. 上海: 同济大学出版社, 1993: 43-57.
|
| [26] |
朱汉卿, 贾爱林, 位云生, 等. 昭通示范区龙马溪组页岩微观孔隙结构特征及吸附能力[J]. 油气地质与采收率, 2018, 25(4): 1-6, 15. ZHU Hanqing, JIA Ailin, WEI Yunsheng, et al. Characteristics of microscopic pore structure and methane adsorption capacity of shale in the Longmaxi Formation in the Zhaotong Area[J]. Petroleum Geology and Recovery Efficiency, 2018, 25(4): 1-6, 15. doi: 10.13673/j.cnki.cn37-1359/te.2018.04.001 |
| [27] |
李全中, 蔡永乐, 胡海洋. 泥页岩中黏土矿物纳米孔隙结构特征及其对甲烷吸附的影响[J]. 煤炭学报, 2017, 42(9): 2414-2419. LI Quanzhong, CAI Yongle, HU Haiyang. Characteristics of nano-pore structure of clay minerals in shale and its effects on methane adsorption capacity[J]. Journal of China Coal Society, 2017, 42(9): 2414-2419. doi: 10.13225/j.cnki.jccs.2017.0097 |
| [28] |
梁洪彬, 向祖平, 肖前华, 等. 页岩气吸附模型对比分析与应用[J]. 大庆石油地质与开发, 2017, 36(6): 159-167. LIANG Hongbin, XIANG Zuping, XIAO Qianhua, et al. Comparative analysis and application of the shale gas absorbing model[J]. Petroleum Geology and Oilfield Development in Daqing, 2017, 36(6): 159-167. doi: 10.19597/J.ISSN.1000-3754.201704083 |
| [29] |
李传亮. 油藏工程原理[M]. 2版. 北京: 石油工业出版社, 2011: 77-79. LI Chuanliang. Reservoir engineering principles[M]. 2nd ed. Beijing: Petroleum Industry Press, 2011: 77-79. |
| [30] |
梁洪彬, 戚志林, 向祖平, 等. 超临界页岩气密度特征研究[J]. 油气藏评价与开发, 2017, 7(5): 74-79. LIANG Hongbin, QI Zhilin, XIANG Zuping, et al. Research on the characteristics of the density of supercritical shale gas[J]. Reservoir Evaluation and Development, 2017, 7(5): 74-79. doi: 10.3969/j.issn.2095-1426.2017.05.014 |
 2020, Vol. 42
2020, Vol. 42