2. 中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580;
3. 中国石化中原油田分公司勘探开发研究院, 河南 濮阳 457001;
4. 中海石油渤海石油管理局渤南作业公司, 天津 塘沽 300452
2. School of Geoscience, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
3. Exploration and Development Institute, Zhongyuan Oilfield Company, Puyang, Henan 457001, China;
4. Bonan Operation Company, Bohai Petroleum Administration, Tanggu, Tianjin 300452, China
地应力是地壳内部应力的总和,一般认为,地应力主要由上覆岩层重力、地层压力、构造应力等方面构成[1-2]。地应力影响油气运聚[3-4]、断层封闭性[5-6]、构造裂缝与压裂裂缝预测[7-8]、井壁稳定性[9-10]及井网部署[11-13],是石油天然气领域不可或缺的数据[10, 14-16]。
地应力的概念从20世纪初被提出以来,人们对地应力的认识与研究经历了由浅到深的过程。地应力的测量方法、技术以及研究手段不断地改进与发展。目前,基于岩芯或井孔的地应力测量是明确地应力状态最直接、有效且成熟的手段,基于测井资料的地应力计算能够获取全井段连续的地应力数据,是地应力测量的重要补充[17]。近年来,数值计算法在三维地应力的研究中应用愈加广泛,以井点地应力值为约束,采用一定的算法,包括遗传算法、神经网络法及模糊算法等[18-19],开展区域应力场预测。然而,受岩芯样品和测试成本的局限,地应力测量无法大规模开展,测井资料所计算的单井地应力状态也难以反映盆地或油藏整体应力场分布特征。虽然数值计算法在理论上具有便捷、经济且准确的三维预测结果,但往往受限于样本数量的不足,对地质条件复杂的地区不具备较强适用性[17]。
目前,基于单井约束的应力场有限元数值模拟法是一种应用广泛、适用性强、精度较高的预测方法,在复杂断块区、非均质较强的深层浊积砂体以及物性特征多变的煤田区块都取得了成功应用[17, 20-21],经历数十年来的发展,学者们进行了多层面的改进与创新,实现了从简单二维均质力学模型到复杂三维非均质力学模型的转变。然而,在进行应力场预测的工作中,为了得到一种最优的加载方式,来达到预测的应力场井点处大小和方向与实测吻合,需要人为地反复尝试确定边界条件。这一过程往往花费较大的精力与时间,特别是对于大型复杂模型,影响研究效率。因此,针对这一问题,笔者基于ANSYS中的APDL语言编译自适应边界程序,将人为调整的过程自动化,实现应力场的智能预测,提高研究效率,并以渤南油田义176区块沙四上亚段的3、4砂组为例,预测其现今地应力场的三维空间分布。
1 研究区概况渤南油田位于济阳拗陷沾化凹陷中部的渤南洼陷内。渤南洼陷是一个北陡南缓向北掀斜的箕状断陷盆地,受几条近东西向盆倾断层切割,从南到北依次形成南部断鼻带、南部断阶带、中部洼陷带和北部陡坡断裂带[22]。义176块位于渤南油田义176—渤深4断阶带,面积49.8 km
研究目的层为沙四上亚段的3、4砂组,各划分为9个小层,埋深3 200
| 表1 义176区块沙四上亚段3、4砂层组非均质参数统计表 Tab. 1 Heterogeneity parameters of lower Four Member of Shahejie Formation, Third and Fourth Sand Group in Yi 176 Block |
基于“横波分裂原理”,根据多极子阵列声波测井资料中的快横波方向能够确定现今地应力方向。由于横波信号在各向异性的地层中传播时会分裂成速度较快的快横波和速度较慢的慢横波,而快横波的传播方向主要沿岩石中天然裂缝的延伸方向或最大主应力方向,通常与地层各向异性相对应,故快横波的传播方向一般就是地层中现今水平最大主应力方向[23-24]。因此,可以通过测量快横波的方位角来确定现今水平最大主应力方向。
通过对义176区块9口具有多极子阵列声波测井数据的井进行测井解释,确定了这9口井在目的层的现今地应力方向(图 1)。可以看出,现今地应力方向主要呈NWW—近EW向,受边界断层控制明显,最大水平主应力方向与断层走向基本一致。
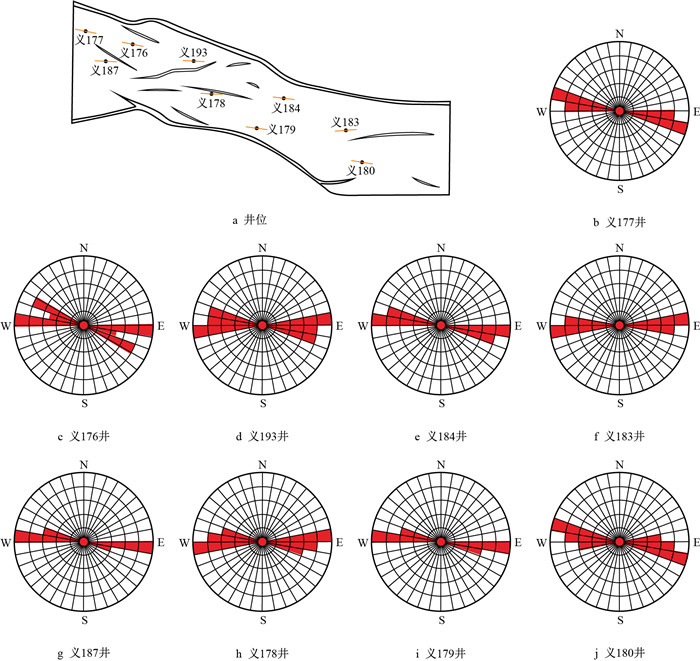 |
| 图1 义176区块实测现今地应力方向 Fig. 1 Measured direction of in-situ stress of Yi 176 Block |
声发射与差应变法是目前相对成熟且较为简单易行的地应力测试方法。
声发射法的原理是脆性材料对曾经的受载作用具有记忆性,通过观察岩样在加载过程中发出的声信号变化,判断Kaiser效应点,进而获得地应力值[25]。为了克服岩石非均质性造成的测试结果误差,从岩芯样品4个方位钻取柱塞样(图 2),分别计算各方位的应力分量,再用式(1)求取主应力的大小。共对义176区块6口井的6组(24块)样品开展了声发射测试,测试结果见表 2。
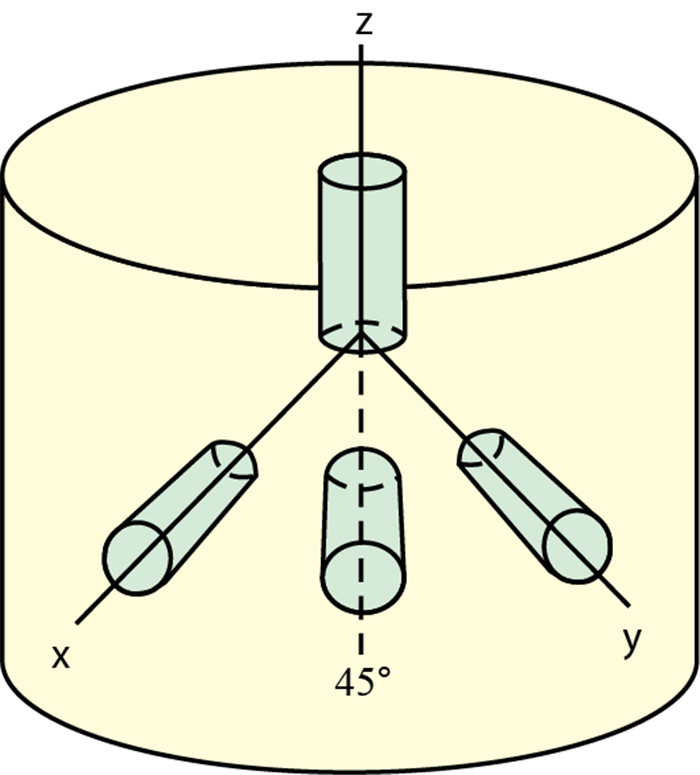 |
| 图2 声发射测试取样示意图 Fig. 2 Sampling schematic diagram of acoustic emission test |
| 表2 义176区块井点实测地应力与预测误差分析 Tab. 2 Error analysis of simulation results of in-situ stress |
差应变法测试现今地应力的原理是,地下岩石取出后发生应力解除从而产生许多张性微裂缝,当对岩石进行应力重新加载,使张开的微裂缝重新闭合,计算微裂缝闭合过程中不同方向上对应的应变张量,即可计算地应力的大小[26]。共对义176区块4口井的4块样品开展了差应变测试,测试结果见表 2。
从井点实测的地应力数据可见,义176区块现今地应力变化范围较大,最大水平主应力为55.21
| $ \left\{ \begin{array}{l} {S_{\rm v}} = {\sigma _ \bot }\\ {S_{\rm H}} = \dfrac{{{\sigma _x} + {\sigma _y}}}{2} + \sqrt {{{\left( {\dfrac{{{\sigma _x} - {\sigma _y}}}{2}} \right)}^2} + {{({\sigma _{x45y}} - \dfrac{{{\sigma _x} + {\sigma _y}}}{2})}^2}} \\ {S_{\rm h}} = \dfrac{{{\sigma _x} + {\sigma _y}}}{2} - \sqrt {{{\left( {\dfrac{{{\sigma _x} - {\sigma _y}}}{2}} \right)}^2} + {{({\sigma _{x45y}} - \dfrac{{{\sigma _x} + {\sigma _y}}}{2})}^2}} \end{array} \right. $ | (1) |
式中:
第一步:构建三维岩石力学场。由于义176区块目的层在平面及垂向上具有较强的非均质性,传统平面均质、纵向分层的力学模型无法满足研究要求。本文通过地震层速度确定三维岩石力学参数,计算方法为
| $ {E_{\rm d}} = {\rho _{\rm b}} v_{\rm s}^2 \dfrac{{3v_{\rm p}^2 - 4v_{\rm s}^2}}{{v_{\rm p}^2 - v_{\rm s}^2}} $ | (2) |
| $ \mu_{\rm{d}} = \dfrac{{v_{\rm p}^2 - 2v_{\rm s}^2}}{{2(v_{\rm p}^2 - v_{\rm s}^2)}} $ | (3) |
式中:
第二步:建立有限元模型。为了提高建模精度,采用Petrel与ANSYS联合建模的方法,首先,利用Petrel进行地质建模,包括层面模型和断层模型;再将层面与断层数据导出,借助autoCAD重构曲面及曲线,接着利用一套自编的插件将模型转化为IGES格式,使ANSYS能够直接识别;然后,进行有限元网格的划分,综合考量模拟精度和运算效率,将断层与地层的网格步长分别设置为150和300,共划分出335 422个节点,1 944 398个单元;最后,将第一步中得到的三维岩石力学参数(包括弹性模量、泊松比及岩石密度)赋予到每一个单元网格中(图 3)。
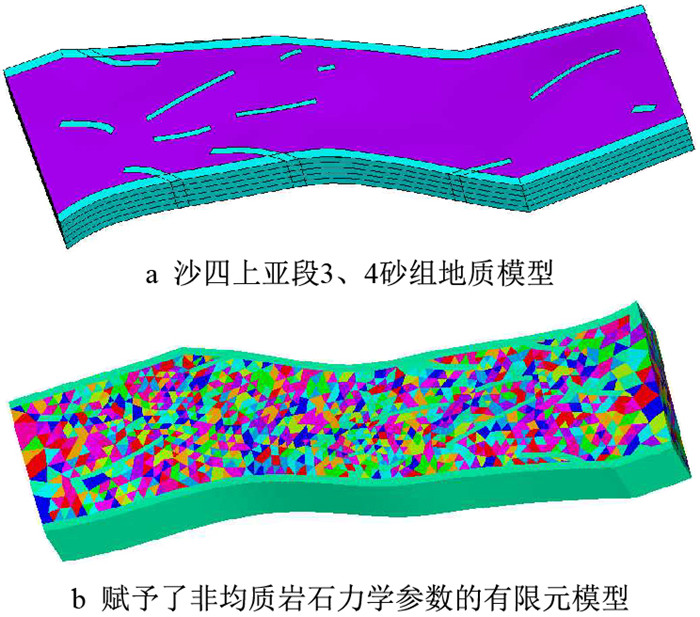 |
| 图3 义176区块三维地质模型及有限元模型 Fig. 3 3D geological model and finite element model of Yi 176 Block |
第三步:最优边界条件确定。首先,根据义176区块所处的大地构造背景初步确定边界条件,设置应力边界条件的初始值;再以图 2和表 2中实测现今地应力方向与大小为约束,编写一种自适应边界程序,不断自动修正边界条件,使模拟结果与实测结果之间的误差达到最小(图 4)。最终以此边界条件进行应力场的数值模拟。
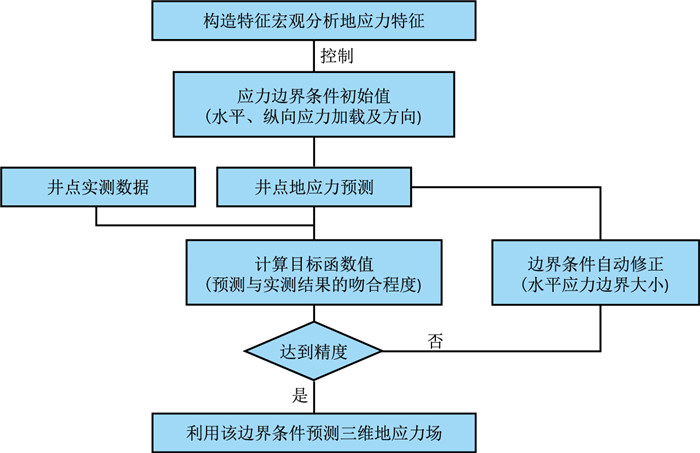 |
| 图4 自适应边界程序的编译流程 Fig. 4 Chart flow of adaptive boundary program |
井点实测值
| $ {\mathit{\boldsymbol{S}}_i} = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i} + {\mathit{\boldsymbol{e}}_i} $ | (4) |
式中:
在整个计算过程中,以井点预测值与实测值的差值函数作为目标函数
| $ \phi ({x_j}) = \sum\limits_{j = 1}^M {e_i^2} $ | (5) |
当目标函数的精度达到要求时,确定合理的边界条件;当目标函数未达到精度要求时,在构造应力宏观分析结果的容忍范围内,对边界条件以一定步长进行不断自动修正,直到目标函数精度达到要求为止。
程序主要包含边界条件加载、数值对比及判断语句循环3个模块。本次研究中,设置初始边界为:北边施加50 MPa压力,南边施加40 MPa压力,东边施加80 MPa压力,西边施加10 MPa的左旋剪切,模拟郯庐断裂的影响。顶面除上覆岩体的重力外,再加30 MPa压力。将表 2的井位坐标和实测应力值输入程序,最大误差设置为10%,应力边界条件为10
通过了30次循环,耗时3 h 25 min,每个井点的相对误差控制在10%以内,达到了预设精度。此时的边界条件为:北边为46 MPa的压力,南边为23 MPa的压力,东边为90 MPa压力,西边的剪切力和顶面的压力保持不变,仍分别为10 MPa和30 MPa(图 5)。
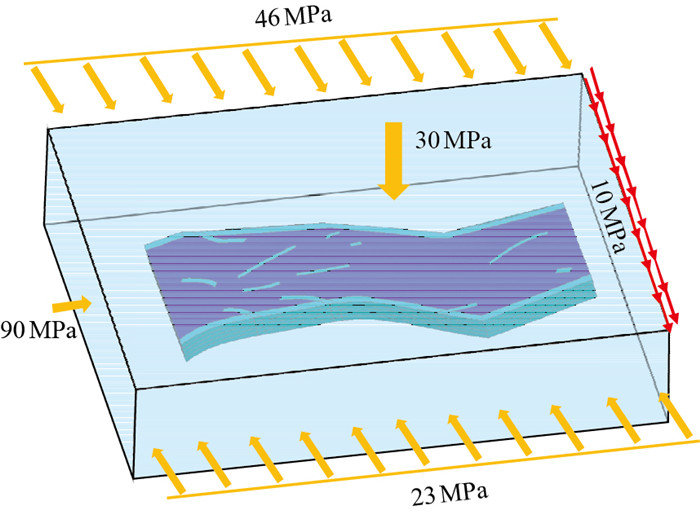 |
| 图5 模型加载方式 Fig. 5 Setting of boundary conditions |
以自适应边界程序最终修正结果为边界条件,通过模拟计算得到义176区块三维应力场分布,包括最大水平主应力(
义176区块应力场整体呈带状分布,应力值有北高南低的趋势,主应力数值分布并不均匀,离散程度较高,多见“牛眼状”的零星展布。最大水平主应力主要在50
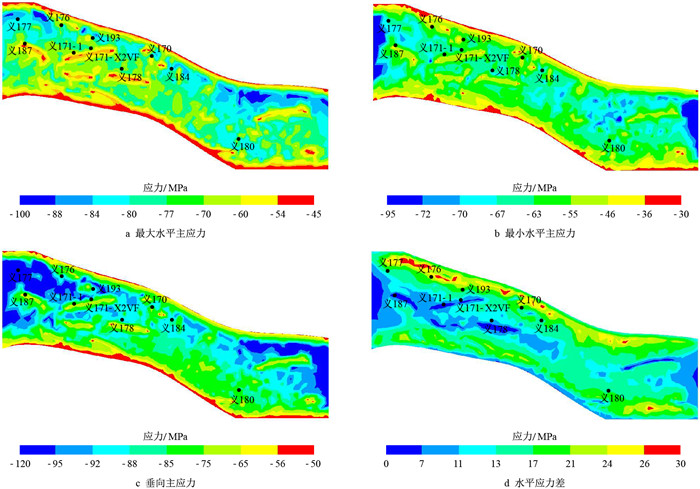 |
| 图6 义176区块现今地应力预测拟结果(负值代表挤压) Fig. 6 Prediction results of in-situ stress of Yi 176 Block(negative values represent compression) |
剖面上,3个主应力与埋深呈线性关系(图 7,式(5)),且表现为
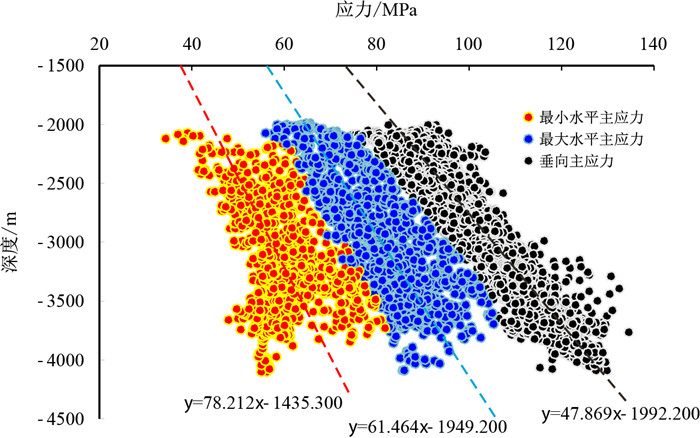 |
| 图7 义176区块3个主应力与埋深的关系 Fig. 7 The relationship between principal stress and depth |
| $ \left\{ \begin{array}{l} {S_{\rm h}} = 0.0128H + 18.3514\\ {S_{\rm H}} = 0.0163H + 31.7129\\ {S_{\rm v}} = 0.0209H + 41.6177 \end{array} \right. $ | (6) |
除了3个主应力外,应力系数也是描述地应力状态的重要参数,包括侧压力系数(
| $ \left\{ \begin{array}{l} {k_{\rm{H/h}}} = {S_{\rm H}}/{S_{\rm h}}\\ k = ({S_{\rm H}} + {S_{\rm h}})/(2{S_{\rm v}}) \end{array} \right. $ | (7) |
侧压力系数是岩体侧向平均应力与垂向应力的比值,是决定岩体稳定性的一个重要参数,其值一般小于1,且随埋深增大而降低。最大和最小水平主应力比值能够反映岩体所受水平应力的状态,可以体现井壁的水平荷载,与水平应力差类似,其数值越小(越近于1),岩体越稳定。
义176区块的侧压力系数呈西低东高的分布趋势,除义180井处于侧压力系数的高值区,其余井点均位于侧压力系数的低值区,其值普遍低于0.8。最大和最小水平主应力比值呈条带状分布,具有南北高、中部低的规律,义176区块内的井点均位于
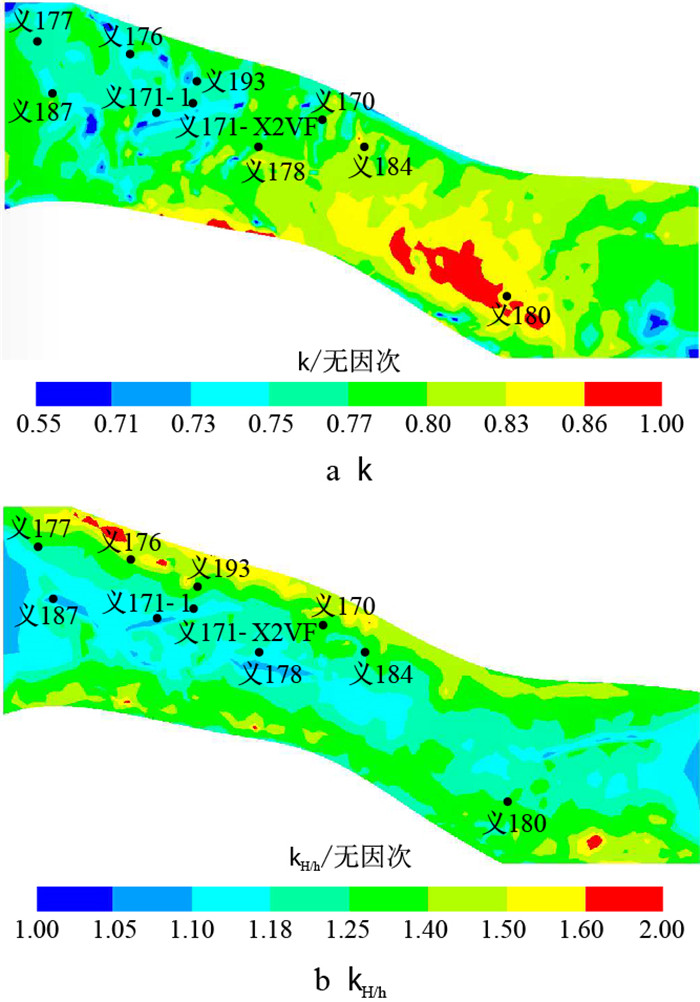 |
| 图8 义176区块应力系数分布图 Fig. 8 Distribution of stress coefficient in Yi 176 Block |
义176区块最大水平主应力方向总体为近EW—SEE,西部主要呈SEE向,向东逐渐转为近EW。得益于自适应边界程序的应用,预测结果与实测结果的吻合程度较高。可以看出,靠近边界断层,最大水平主应力方向顺断层走向偏转,而研究区块内部,应力方向变化微弱,偏转一般不超过10°(图 9)。最小水平主应力与最大水平主应力垂直,方向总体为近NS—NNE。
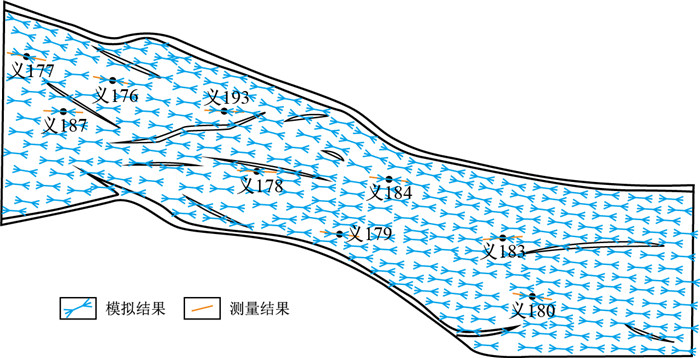 |
| 图9 义176区块最大水平主应力方向实测与预测结果 Fig. 9 Measurement and prediction results of direction of maximum principal stress in Yi 176 Block |
地应力方向会受断层、岩相及构造形态的控制,一般断层的影响较为显著,其规模、走向、充填物以及形态都会引起地应力方向的偏转[30],并且往往会造成应力方向的杂乱,而岩相的非均质性及构造的起伏对应力方向影响比较微弱且均匀。
5 结论(1) 义176区块现今最大水平主应力方向总体呈近EW—SEE向,现今地应力数值变化较大,在目的层范围属于I
(2) 义176区块中部存在一片条带状展布的“应力甜点”,其水平应力差和
(3) 自适应边界程序大幅缩短了人工反复尝试边界条件的时间,提高了应力场模拟的效率,结合Petrel与ANSYS的联合建模法及三维非均质力学模型,进一步完善了三维应力场预测的方法,形成了一套应力场的智能预测技术。
| [1] |
BELL J S. Petro geoscience 2. In-situ stresses in sedimentary rocks (part 2):Applications of stress measurements[J]. Geoscience Canada, 1996, 23(3): 135-153. |
| [2] |
KANG H, ZHANG X, SI L, et al. In-situ stress measurements and stress distribution characteristics in underground coal mines in China[J]. Engineering Geology, 2010, 116(3-4): 333-345. doi: 10.1016/j.enggeo.2010.-09.015 |
| [3] |
TAN Chengxuan, JIN Zhijun, ZHANG Mingli, et al. An approach to the present-day three-dimensional (3D) stress field and its application in hydrocarbon migration and accumulation in the Zhangqiang Depression, Liaohe Field, China[J]. Marine & Petroleum Geology, 2001, 18(9): 983-994. doi: 10.1016/S0264-8172(01)00040-X |
| [4] |
KHAIR H A, COOKE D, HAND M. The effect of present day in situ stresses and paleo-stresses on locating sweet spots in unconventional reservoirs:A case study from Moomba-Big Lake fields, Cooper Basin, South Australia[J]. Journal of Petroleum Exploration & Production Technology, 2013, 3(4): 207-221. doi: 10.1007/s13202-013-0082-x |
| [5] |
王珂, 戴俊生. 地应力与断层封闭性之间的定量关系[J]. 石油学报, 2012, 33(1): 74-81. WANG Ke, DAI Junsheng. A quantitative relationship between the crustal stress and fault sealing ability[J]. Acta Petrolei Sinica, 2012, 33(1): 74-81. |
| [6] |
ZOBACK M D. Reservoir geomechanics[M]. Cambridge: Cambridge University Press, 2007.
|
| [7] |
周文.川西致密储层现今地应力场特征及石油工程地质应用研究[D].成都: 成都理工大学, 2006. ZHOU Wen. The characteristics of in-situ earth stress and its application research in engineering geology of petroleum on compact reservoir in western Sichuan Depression[D]. Chengdu: Chengdu University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10616-2006139827.htm |
| [8] |
冯建伟, 戴俊生, 马占荣, 等. 低渗透砂岩裂缝参数与应力场关系理论模型[J]. 石油学报, 2011, 32(4): 664-671. FENG Jianwei, DAI Junsheng, MA Zhanrong, et al. The theoretical model between fracture parameters and stress field of low-permeability sandstones[J]. Acta Petrolei Sinica, 2011, 32(4): 664-671. |
| [9] |
ZOBACK M D, BARTON C A, BRUDY M, et al. Determination of stress orientation and magnitude in deep wells[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(7-8): 1049-1076. doi: 10.1016/j.-ijrmms.2003.07.001 |
| [10] |
TINGAY M, BENTHAM P, FEYTER A, et al. Presentday stress-field rotations associated with evaporites in the offshore Nile Delta[J]. Geological Society of America Bulletin, 2011, 123(5-6): 1171-1180. doi: 10.1130/B30185.1 |
| [11] |
SIBSON R H. Crustal stress, faulting and fluid flow[J]. Geological Society London Special Publications, 1994, 78(1): 69-84. doi: 10.1144/GSL.SP.1994.078.01.07 |
| [12] |
BINH N T T, TOKUNAGA T, SON H P, et al. Presentday stress and pore pressure fields in the Cuu Long and Nam Con Son Basins, offshore Vietnam[J]. Marine & Petroleum Geology, 2007, 24(10): 607-615. doi: 10.1016/j.-marpetgeo.2007.04.002 |
| [13] |
LIU Jingshou, DING Wenlong, YANG Haimeng, et al. 3D geomechanical modeling and numerical simulation of in-situ stress fields in shale reservoirs:A case study of the lower Cambrian Niutitang Formation in the Cen'gong Block, South China[J]. Tectonophysics, 2017, 712-713: 663-683. doi: 10.1016/j.tecto.2017.06.030 |
| [14] |
LI Yong, TANG Dazhan, XU Hao, et al. In-situ stress distribution and its implication on coalbed methane development in Liulin Area, eastern Ordos Basin, China[J]. Journal of Petroleum Science & Engineering, 2014, 122: 488-496. doi: 10.1016/j.petrol.2014.08.010 |
| [15] |
JU Wei, SUN Weifeng. Tectonic fractures in the Lower Cretaceous Xiagou Formation of Qingxi Oilfield, Jiuxi Basin, NW China. Part two:Numerical simulation of tectonic stress field and prediction of tectonic fractures[J]. Journal of Petroleum Science & Engineering, 2016, 146: 626-636. doi: 10.1016/j.petrol.2016.05.002 |
| [16] |
JU Wei, SHEN Jian, QIN Yong, et al. In-situ stress state in the Linxing Region, eastern Ordos Basin, China:Implications for unconventional gas exploration and production[J]. Marine & Petroleum Geology, 2017, 86: 67-78. doi: 10.1016/j.marpetgeo.2017.05.026 |
| [17] |
徐珂, 戴俊生, 冯建伟, 等. 南堡凹陷高深北区三维非均质应力场精细预测[J]. 中国矿业大学学报, 2018, 47(6): 1357-1367. XU Ke, DAI Junsheng, FENG Jianwei, et al. Prediction of 3D heterogeneous in-situ stress field of Northern area in Gaoshen, Nanpu Sag, Bohai Bay Basin, China[J]. Journal of China University of Mining & Technology, 2018, 47(6): 1357-1367. doi: 10.13247/j.cnki.jcumt.000869 |
| [18] |
王金安, 李飞. 复杂地应力场反演优化算法及研究新进展[J]. 中国矿业大学学报, 2015, 44(2): 189-205. WANG Jin'an, LI Fei. Review of inverse optimal algorithm of and new achievement in-situ stress field[J]. Journal of China University of Minim & Technology, 2015, 44(2): 189-205. doi: 10.13247/j.cnki.jcumt.000292 |
| [19] |
李永松, 艾凯, 尹健民. 基于VB与Matlab的BP神经网络在地应力场分析中的应用[J]. 长江科学院院报, 2009, 26(6): 24-27. LI Yongsong, AI Kai, YIN Jianmin. Application of BP network based on VB and MATLAB in analysis of insitu stress field[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(6): 24-27. doi: 10.3969/j.issn.1001-5485.2009.06.007 |
| [20] |
朱传华, 王伟锋, 王青振, 等. 非均质储层三维构造应力场模拟方法[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1580-1588. ZHU Chuanhua, WANG Weifeng, WANG Qingzhen, et al. Numerical simulation of structural strain for Turbidite Sands Reservoirs of Low Permeability[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1580-1588. doi: 10.13278/j.cnki.jjuese.201605306 |
| [21] |
FU Xiaolong, DAI Junsheng, FENG Jianwei. Prediction of tectonic fractures in coal reservoirs using geomechanical method[J]. Geosciences Journal, 2018, 22(4): 589-608. doi: 10.1007/s12303-017-0072-y |
| [22] |
朱淼.胜利油田义176块沙四上亚段三、四砂组储层评价[D].武汉: 长江大学, 2014. ZHU Miao. The reservoir evaluation of the upper section of Sha-4, third and fourth sand group in Yi 176, Shengli Oilfield[D]. Wuhan: Changjiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10489-1014345332.htm |
| [23] |
赖富强, 孙建孟, 苏远大, 等. 利用多极子阵列声波测井预测地层破裂压力[J]. 勘探地球物理进展, 2007, 30(1): 39-42. LAI Fuqiang, SUN Jianmeng, SU Yuanda, et al. Prediction of fracture pressure using mufti-pole array acoustic logging[J]. Progress in Exploration Geophysics, 2007, 30(1): 39-42. |
| [24] |
班勇凯, 曾玉峰, 韩雪, 等. 正交多极子阵列声波测井资料在桩西油田压裂中的应用[J]. 油气井测试, 2015, 24(4): 35-37. BAN Yongkai, ZENG Yufeng, HAN Xue, et al. Application of cross multipole array acoustic logging data in fracturing operation of Zhuangxi Oilfield[J]. Well Testing, 2015, 24(4): 35-37. doi: 10.3969/j.issn.1004-4388.2015.04.010 |
| [25] |
彭瑞, 孟祥瑞, 赵光明, 等. 不同岩性岩石声发射地应力测试及其应用[J]. 中南大学学报(自然科学版), 2015, 46(9): 3377-3384. PENG Rui, MENG Xiangrui, ZHAO Guangming, et al. Acoustic emission in-situ stress testing of different lithology rock and its application[J]. Journal of Central South University (Science and Technology), 2015, 46(9): 3377-3384. doi: 10.11817/j.issn.672-7207.2015.-09.030doi:10.11817/j.issn.1672-7207.2015.09.030 |
| [26] |
尹帅, 丁文龙, 高敏东, 等. 樊庄北部3号煤层现今应力场分布数值模拟[J]. 西南石油大学学报(自然科学版), 2017, 39(4): 81-89. YIN Shuai, DING Wenlong, GAO Mindong, et al. The in-situ stress field distribution numerical simulation of No.3 Coal Seam in the North of Fanzhuang CBM Well Blocks[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(4): 81-89. doi: 10.11885/j.issn.1674-5086.2015.06.02.02 |
| [27] |
董建华, 刘鹏, 王薇. 地应力剖面在水力压裂施工中的应用[J]. 大庆石油学院学报, 2005, 29(2): 40-42. DONG Jianhua, LIU Peng, WANG Wei. Application of in situ stress profile to hydraulic fracturing[J]. Journal of Daqing Petroleum Insitute, 2005, 29(2): 40-42. |
| [28] |
SAVAGE W Z, SWOLFS H S, AMADEI B. On the state of stress in the near-surface of the earth's crust[J]. Pure & Applied Geophysics, 1992, 138(2): 207-228. doi: 10.1007/BF00878896 |
| [29] |
李传亮, 朱苏阳. 关于岩石侧压系数的认识误区[J]. 西南石油大学学报(自然科学版), 2017, 39(3): 135-140. LI Chuanliang, ZHU Suyang. On misunderstandings of the rock lateral pressure coefficient[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(3): 135-140. doi: 10.11885/j.issn.1674-5086.2015.10.26.01 |
| [30] |
苏生瑞.断裂构造对地应力场的影响及其工程意义[D].成都: 成都理工学院, 2001. SU Shengrui. Effect of fractures on rock stresses and its significance in geological engineering[D]. Chengdu: Chengdu University of Technology, 2001. |
 2019, Vol. 41
2019, Vol. 41


