随着渤海油田勘探程度不断加深,以潜山为代表的裂缝性油气藏日益增多,成为储量的重要组成部分。此类储层受裂缝发育的影响,储层孔隙结构较为复杂,简单的孔隙度模型难以准确表征储层孔隙结构特征,测井曲线响应特征进一步复杂化。因此,裂缝的分布特征及裂缝孔隙度将直接影响储层的品质,准确获取裂缝分布特征及裂缝孔隙度是测井解释的重点,直接影响地质建模[1]、油藏开发[2]等油田生产工作。
目前,裂缝评价以定性为主,通常以岩芯描述[3]为基础,利用常规、电成像测井、阵列声波测井等开展综合评价。电成像测井是裂缝评价较为直观的工具,可以拾取裂缝产状、计算裂缝密度与开度[4-5],为储层裂缝有效性评价提供参考依据。李善军等利用双侧向测井响应特征提出裂缝孔隙度计算方法[6],在此基础上,王晓畅等通过电成像测井给出裂缝孔隙度的定量计算,较为准确地描述了裂缝孔隙度大小,是电法测井计算裂缝孔隙度较为合理的一种方式[7],但未考虑泥浆侵入[8]的影响。阵列声波测井在储层裂缝评价中具有很大优势,裂缝对岩石力学、声学特征有较大影响,在定性、定量方面均取得较大进展。夏宏泉等基于裂缝产生的各向异性提取横波分裂数据,进而定性检测裂缝发育程度[9-10]。罗利等通过声波远探测技术识别井眼周围地层宏观裂缝发育特征,对井外地层宏观缝拾取提供一种有效方法,但无法识别尺度较小的裂缝[11]。岩石的弹性性质依赖于孔隙系统的微观结构,因此利用岩石弹性参数评价裂缝特征是计算裂缝孔隙度的基础。吕洪志[12]等在Biot相洽理论[13]基础上不考虑其他因素影响对裂缝孔隙度进行了反演,Tang[14]等通过对Biot理论[15]进行改进,引入裂隙参数形成孔-裂隙理论,Chen等对孔-裂隙理论波动方程进行推导,模拟裂缝对弹性参数的影响,为裂缝孔隙度计算奠定基础[16]。李宏兵等通过引入等效介质理论对多孔隙岩石弹性性质进行描述,给出微分等效介质理论解析解,结合Gassmann方程反演等效孔隙纵横比,半定量描述裂缝发育特征,未给出裂缝分布状态[17-18]。此外,陆云龙等通过三维莫尔圆定量评价裂缝有效性,对裂缝产液贡献能力进行定量评价,但无法计算裂缝孔隙度大小[19]。
本文基于等效介质理论的多孔介质模型,提出利用孔隙纵横比谱分布函数定量描述孔隙裂缝分布特征,并将该函数引入到传统等效介质模型当中,建立新的等效介质模型,总结孔隙纵横比谱与岩石体积模量之间的变化规律,根据阵列声波测井资料反演孔隙纵横比谱分布特征,定量计算裂缝孔隙度。
1 基于孔隙纵横比谱分布的多孔介质模型 1.1 微分等效介质模型选取岩石物理模型是描述地下岩石组分、孔隙、流体等所表现出的宏观弹性、非弹性特征,由于地下岩石复杂多变,通常采用等效介质模型近似表征岩石弹性模量参数变化规律。等效介质模型通常认为,岩石是各向同性、线性、弹性介质,在此基础上,通过孔隙结构特征、孔隙流体性质综合求取岩石等效弹性模量。Kuster等根据长波长一阶散射理论推导了纵波与横波速度的表达式,描述包含
| $ \left \{ \begin{array}{l} (1-\phi )\dfrac{{\rm d}{{K}^{*}}(\phi )}{{\rm d}\phi }=\sum\limits_{i=1}^{N}{{{\upsilon }_{i}}[{{K}_{i}}-{{K}^{*}}(\phi )]{{P}^{*i}}} \\ (1-\phi )\dfrac{{\rm d}{{G}^{*}}(\phi )}{{\rm d}\phi }=\sum\limits_{i=1}^{N}{{{\upsilon }_{i}}[{{G}_{i}}-{{G}^{*}}(\phi )]{{Q}^{*i}}} \\ \end{array} \right . $ | (1) |
式中:
对于任意孔隙纵横比所对应的椭球状包裹物的
| $ \left\{ \begin{array}{l} {{P}^{*i}}=\dfrac{1\!+\!A[3(f\!+\!\theta )/2\!-\!R(3f/2\!+\!5\theta /2\!-\!4/3]}{{{F}_{1}}} \\[5pt] {{Q}^{*i}}=\dfrac{2}{5{{F}_{2}}}\!+\!\dfrac{1}{5{{F}_{3}}}\!+\!\dfrac{{{F}_{3}}{{F}_{4}}\!+\!{{F}_{5}}{{F}_{6}}-{{F}_{7}}{{F}_{8}}}{{{F}_{1}}{{F}_{3}}} \\ {{F}_{1}}=1+A[1+3(f+\theta )/2+R(3f+5\theta )/2]+\\{\kern 40pt}B(3-4R)+A(A+3B)(3-4R)\\{\kern 40pt}[f+\theta -R(f-\theta +2{{\theta }^{2}})]/2 \\ {{F}_{2}}=1+A[1-(f+3\theta /2)+R(f+\theta )] \\ {{F}_{3}}=1+A[f+3\theta -R(f-\theta )]/4 \\ {{F}_{4}}=A[-f+R(f+\theta -4/3)]+B\theta (3-4R) \\ {{F}_{5}}=1+A[1+f-R(f+\theta )]+\\{\kern 40pt}B(1-\theta )(3-4R) \\ {{F}_{6}}=2+A[3f+9\theta -R(3f+5\theta )]/4+\\{\kern 40pt}B\theta (3-4R) \\ {{F}_{7}}=A[1-2R+f(R-1)/2+\theta (5R-3)/2]+\\{\kern 40pt}B(1-\theta )(3-4R) \\ {{F}_{8}}=A[f(R-1)-R\theta ]+B\theta (3-4R) \\ A={{G}_{i}}/{{G}_{\rm m}}-1 \\ B=({{K}_{i}}/{{K}_{\rm m}}-{{G}_{i}}/{{G}_{\rm m}})/3 \\ R=(1-2{{\nu }_{\rm m}})/(1-{{\nu }_{\rm m}})/2 \\ f={{\alpha }^{2}}/(1-{{\alpha }^{2}})(3\theta -2) \\ \theta =\alpha [\arccos (\alpha )-\alpha {{(1-{{\alpha }^{2}})}^{0.5}}]/{{(1-{{\alpha }^{2}})}^{3/2}} \\ \end{array} \right. $ | (2) |
式中:
储层岩石由颗粒骨架与孔隙两部分组成,其中孔隙由不同类型孔隙形状组成的复杂孔隙结构,因此可以通过一系列简单的几何形状组成的孔隙分布近似描述孔隙特征,如图 1所示。
 |
| 图1 岩石孔隙结构简化模型示意图 Fig. 1 The diagrammatic sketch for simplified model of the rock pore structure |
不同类型储层岩石孔隙结构不同,几何形状及所占百分比差异较大,几何形状可以采用孔隙纵横比进行描述,即孔隙中短轴与长轴的比值所确定的椭球状孔隙,如图 2a(其中,
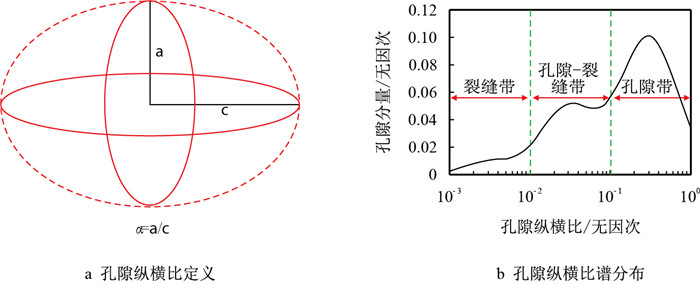 |
| 图2 孔隙纵横比定义及孔隙纵横比谱分布特征 Fig. 2 The definition of pore aspect ratio and pore aspect ratio spectrum distribution |
不同孔隙纵横比对应的孔隙类型及所占百分比不同,当储层岩石孔隙结构复杂时,单一等效岩石孔隙纵横比并不能较好地反映孔隙结构特征,此时可以将岩石孔隙结构划分成一系列不同孔隙纵横比及所对应的孔隙分量,形成孔隙纵横比谱分布,如图 2b所示。孔隙纵横比谱分布可较为精确地描述孔隙结构特征,同时将孔隙按照不同孔隙纵横比划分为裂缝带、过渡带和孔隙带3个区间,每个区间按对数刻度,其中,裂缝带孔隙纵横比为[0.001,0.010);过渡带孔隙纵横比为[0.010,0.100);孔隙带孔隙纵横比为[0.100,1.000)。
根据孔隙纵横比谱分布的定义及特征,通过式(3)对其进行定量描述
| $ {{\upsilon}_{i}}={{H}_{1}}{{\rm e}^{-\frac{{{(\lg {{\alpha }_{i}}+2.4)}^{2}}}{0.18}}}\!+\!{{H}_{2}}{{\rm e}^{-\frac{{{(\lg {{\alpha }_{i}}+1.4)}^{2}}}{0.18}}}\!+\!{{H}_{3}}{{\rm e}^{-\frac{{{(\lg {{\alpha }_{i}}+0.4)}^{2}}}{0.18}}}%\\{\kern 40pt} $ | (3) |
式中:
为方便计算,孔隙纵横比按对数布点,分布在0.001
将式(3)代入式(1),即可得到含孔隙纵横比谱分布的多孔介质模型,由于模型是耦合的,同时通过迭代的方法,采用四阶龙格-库塔算法求取数值解。当孔隙结构特征发生变化时,不同孔隙纵横比所对应的孔隙体积改变,导致孔隙纵横比谱发生变化,使得式(1)的数值解相应变化。当储层包含裂缝时,裂缝带孔隙所占比例发生变化,进而导致岩石模量发生变化,从而确定裂缝发育情况。
图 3为选取3种不同类型孔隙结构特征的孔隙纵横比谱(分别为孔隙型、孔隙-裂缝型、裂缝型储层),将式(3)代入式(1)求解模型所得的数值解,从而得到不同孔隙纵横比谱分布下岩石体积模量变化规律,其中,骨架体积模量、剪切模量分别取44和37 GPa,流体模量取0。结果表明,当孔隙流体性质一定时,不同孔隙纵横比谱分布与多孔介质模型计算的岩石体积模量具有一一对应关系,即相同孔隙度条件下,当孔隙不包含裂缝时,岩石体积模量最高,随着裂缝孔隙体积不断增多,岩石体积模量逐渐降低。
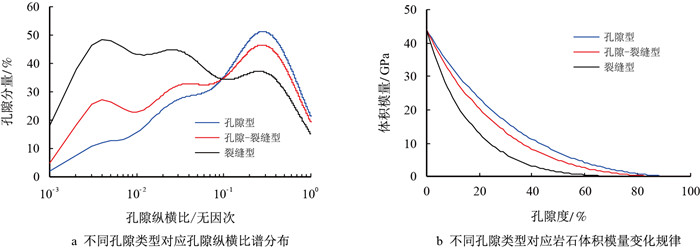 |
| 图3 不同孔隙类型岩石体积模量变化特征 Fig. 3 Variation characteristics of bulk modulus corresponding to different pore structure |
当孔隙度、流体性质一定时,岩石孔隙纵横比谱分布与体积模量具有较好的对应关系,因此根据测井资料确定的岩石模量值与多孔介质模型数值解建立目标函数,通过反演确定式(3)中函数的参数
| $ E=\dfrac{|K-{{K}^{*}}(\phi ){{|}^{2}}}{{{K}^{2}}}+\dfrac{|G-{{G}^{*}}(\phi ){{|}^{2}}}{{{G}^{2}}} $ | (4) |
式中:
式(4)反演过程中,可根据岩芯分析、铸体薄片、核磁共振、电成像等资料对式(3)中待求参数分布范围进行约束,减小反演计算量与无效解,提升反演精度。反演结果确定的孔隙纵横比谱分布代表储层真实孔隙结构(图 4)。
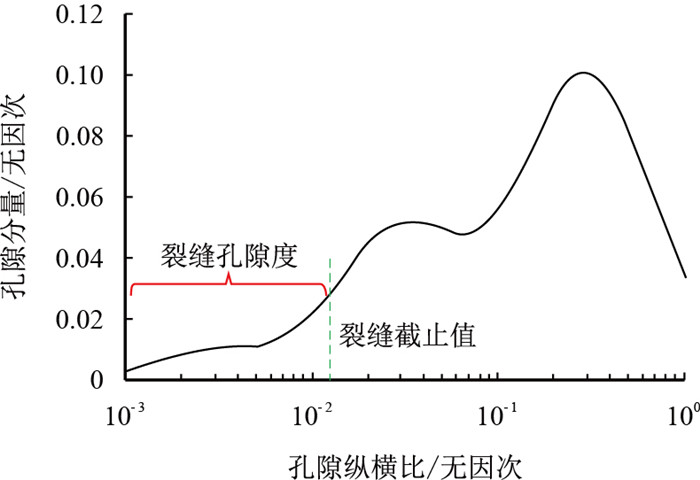 |
| 图4 裂缝孔隙度计算示意图 Fig. 4 Fracture porosity computation method sketch map |
在反演确定的孔隙纵横比谱分布基础上,通过铸体薄片等资料确定裂缝所对应的最大孔隙纵横比,或根据储层非裂缝发育层段所对应的最小孔隙纵横比确定储层裂缝截止值。裂缝截止值反映储层裂缝所对应的最大孔隙纵横比,小于该值的所有孔隙纵横比所对应的孔隙分量相加即得到裂缝孔隙度,如图 4所示。裂缝孔隙度确定公式为
| $ {{\phi }_{\rm f}}=\phi \sum\limits_{i=1}^{m}{{{\upsilon}_{i}}} $ | (5) |
式中:
锦州25-1S油气田位于渤海辽西低凸起中段[25],太古宇潜山发育块状油藏,岩性为区域变质花岗片麻岩,顶部风化较严重,储集空间具有孔洞、缝并存,非均质程度较高的双重孔隙介质特征,裂缝错综复杂,低角度、高角度、网状缝均发育,储层裂缝评价对油田地质认识、油藏开发具有重要意义。
图 5为锦州25-1S油气田2井裂缝评价效果图。
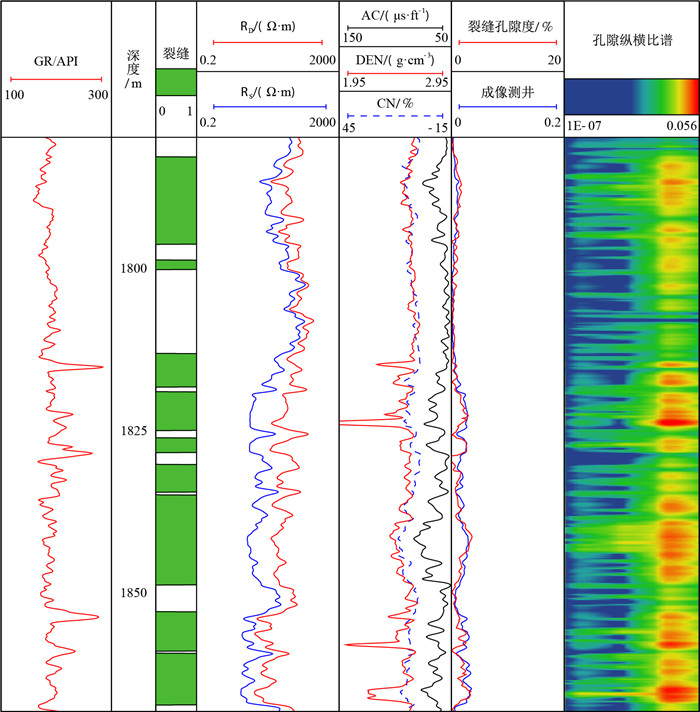 |
| 图5 裂缝孔隙度反演结果及精度分析 Fig. 5 The results of fracture porosity inversion and accuracy analysis |
利用式(1)
图 6统计了渤海不同类型岩性油气藏裂缝孔隙度计算结果与成像测井计算结果的对比效果,包括花岗岩潜山、变质岩潜山、碳酸盐岩潜山等裂缝性油气藏。对比发现,不同类型储层,裂缝孔隙度计算结果与成像测井计算结果吻合较好,两者误差较小,能够满足测井解释精度要求,同时也证实阵列声波测井裂缝孔隙度计算方法适用于不同类型储层,对于渤海复杂岩性储层裂缝孔隙度计算具有较好的推广应用价值。
 |
| 图6 裂缝孔隙度计算精度分析 Fig. 6 Accuracy analysis of fracture porosity results |
(1) 提出孔隙纵横比谱概念,通过数学表达式对孔隙纵横比谱进行描述,刻画孔隙结构特征。
(2) 将孔隙纵横比谱引入微分等效介质模型中,建立阵列声波多孔介质模型,该模型在孔隙度、流体性质相同条件下与孔隙结构分布具有较好的对应关系。
(3) 基于孔隙纵横比谱的多孔介质模型,结合阵列声波测井资料建立裂缝孔隙度定量反演函数,实现裂缝孔隙度定量计算,应用效果较好。
| [1] |
刘建军, 吴明洋, 宋睿, 等. 低渗透油藏储层多尺度裂缝的建模方法研究[J]. 西南石油大学学报(自然科学版), 2017, 39(4): 90-103. LIU Jianjun, WU Mingyang, SONG Rui, et al. Study on simulation method of multi-scale fractures in low permeability reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(4): 90-103. doi: 10.11885/j.issn.1674-5086.2016.06.25.03 |
| [2] |
商克俭, 冯冬梅, 叶礼友, 等. 裂缝-孔隙型双重介质气藏开发影响分析[J]. 西南石油大学学报(自然科学版), 2018, 40(2): 107-114. SHANG Kejian, FENG Dongmei, YE Liyou, et al. Analysis of the influence of the development of fracture-porosity volcanic gas reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(2): 107-114. doi: 10.11885/j.issn.1674-5086.2017.01.08.02 |
| [3] |
赵向原, 胡向阳, 曾联波, 等. 四川盆地元坝地区长兴组礁滩相储层天然裂缝有效性评价[J]. 天然气工业, 2017, 37(2): 52-61. ZHAO Xiangyuan, HU Xiangyang, ZENG Lianbo, et al. Evaluation on the effectiveness of natural fractures in reefflat facies reservoirs of Changxing Fm in Yuanba Area, Sichuan Basin[J]. Natural Gas Exploration and Development, 2017, 37(2): 52-61. doi: 10.3787/j.issn.1000-0976.-2017.02.007 |
| [4] |
张树东, 任兴国, 罗利, 等. 阿姆河右岸东部地区岩溶裂缝的测井识别与评价[J]. 天然气工业, 2018, 38(6): 53-58. ZHANG Shudong, REN Xingguo, LUO Li, et al. Loggingbased identification and evaluation of karst fractures in the eastern Right Bank of the Amu Darya River of Turkmenistan[J]. Natural Gas Exploration and Development, 2018, 38(6): 53-58. doi: 10.3787/j.issn.1000-0976.2018.-06.007 |
| [5] |
齐宝权, 赵佐安, 贺洪举, 等. 应用测井储层品质综合评价指数来判别储层的有效性——以四川盆地西部地区二叠系栖霞组为例[J]. 天然气工业, 2018, 38(2): 25-32. QI Baoquan, ZHAO Zuoan, HE Hongju, et al. Reservoir effectiveness evaluation based on comprehensive reservoir quality evaluation indexes of well logging:A case study on the Permian Qixia Fm in the western Sichuan Basin[J]. Natural Gas Exploration and Development, 2018, 38(2): 25-32. doi: 10.3787/j.issn.1000-0976.-2018.02.004 |
| [6] |
李善军, 肖承文, 汪涵明, 等. 裂缝的双侧向测井响应的数学模型及裂缝孔隙度的定量解释[J]. 地球物理学报, 1996, 39(6): 845-852. LI Shanjun, XIAO Chengwen, WANG Hanming, et al. Mathematical model of dual laterolog response to fracture and quantitative interpretation of fracture porosity[J]. Acta Geophysica Sinica, 1996, 39(6): 845-852. doi: 10.3321/j.issn:0001-5733.1996.06.014 |
| [7] |
王晓畅, 李军, 张松扬, 等. 基于测井资料的裂缝面孔率标定裂缝孔隙度的数值模拟及应用[J]. 中国石油大学学报(自然科学版), 2011, 35(2): 51-56. WANG Xiaochang, LI Jun, ZHANG Songyang, et al. Numerical simulation and application of fracture surface porosity calibrating fracture porosity by logging data[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(2): 51-56. doi: 10.3969/j.issn.1673-5005.2011.02.009 |
| [8] |
雷强, 唐洪明, 张烈辉, 等. 钻井液在致密砂岩中裂缝的侵入深度模型[J]. 西南石油大学学报(自然科学版), 2018, 40(4): 97-104. LEI Qiang, TANG Hongming, ZHANG Liehui, et al. Invasion depth model for drilling fluids in fractures in dense sandstones[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(4): 97-104. doi: 10.11885/j.issn.1674-5086.2017.04.25.03 |
| [9] |
夏宏泉, 郭倩男. 基于DSI测井横波分裂的水平井压裂缝检测研究[J]. 西南石油大学学报(自然科学版), 2018, 40(3): 87-96. XIA Hongquan, GUO Qiannan. Detection of hydraulic fractures in horizontal wells based on shear wave splitting of DSI logging[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(3): 87-96. doi: 10.11885/j.issn.1674-5086.2016.12.20.03 |
| [10] |
谢冰, 白利, 赵艾琳, 等. Sonic Scanner声波扫描测井在碳酸盐岩储层裂缝有效性评价中的应用——以四川盆地震旦系为例[J]. 岩性油气藏, 2017, 29(4): 117-123. XIE Bing, BAI Li, ZHAO Ailin, et al. Application of sonic scanner logging to fracture effectiveness evaluation of carbonate reservoir:A case from Sinian in Sichuan Basin[J]. Lithologic Reservoirs, 2017, 29(4): 117-123. doi: 10.3969/j.issn.1673-8926.2017.04.014 |
| [11] |
罗利, 刘航, 刘海军, 等. XMAC-F1反射横波远探测成像技术及其应用[J]. 天然气工业, 2017, 37(6): 28-33. LUO Li, LIU Hang, LIU Haijun, et al. XMAC-F1 reflected-shear-wave remote detection imaging technology and its application[J]. Natural Gas Industry, 2017, 37(6): 28-33. doi: 10.3787/j.issn.1000-0976.2017.06.004 |
| [12] |
吕洪志, 陆云龙, 崔云江, 等. 改进的孔隙模型评价流体性质与裂缝孔隙度[J]. 应用声学, 2016, 35(4): 351-356. LÜ Hongzhi, LU Yunlong, CUI Yunjiang, et al. Improved porosity model for fluid nature and fracture porosity evaluation[J]. Journal of Applied Acoustics, 2016, 35(4): 351-356. doi: 10.11684/j.issn.1000-310X.2016.04.010 |
| [13] |
THOMSEN L. Biot-consistent elastic moduli of porous rocks:Low-frequency limit[J]. Geophysics, 1985, 50(12): 2797-2807. doi: 10.1190/1.1441900 |
| [14] |
TANG Xiaoming, CHEN Xuelian, XU Xiaokai. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations[J]. Geophysics, 2012, 77(6): 245-252. doi: 10.1190/geo2012-0091.1 |
| [15] |
BIOT M A. Generalized theory of acoustic propagation in porous dissipative media[J]. The Journal of The Acoustical Society of America, 1962, 34(9): 1254-1264. doi: 10.1121/1.1918315 |
| [16] |
CHEN Xuelian, TANG Xiaoming, QIAN Yuping. Simulation of multipole acoustic logging in cracked porous formations[J]. Geophysics, 2013, 79(1): 1-10. doi: 10.1190/-geo2013-0163.1 |
| [17] |
李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J]. 地球物理学报, 2014, 57(10): 3422-3430. LI Hongbing, ZHANG Jiajia. A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J]. Chinese Journal of Geophysics, 2014, 57(10): 3422-3430. doi: 10.6038/-cjg20141028 |
| [18] |
李宏兵, 张佳佳, 姚逢昌. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 2013, 56(2): 608-615. LI Hongbing, ZHANG Jiajia, YAO Fengchang. Inversion of effective pore aspect ratios for porous rocks and its applications[J]. Chinese Journal of Geophysics, 2013, 56(2): 608-615. doi: 10.6038/cjg20130224 |
| [19] |
陆云龙, 吕洪志, 崔云江, 等. 基于三维莫尔圆的裂缝有效性评价方法及应用[J]. 石油学报, 2018, 39(5): 564-569. LU Yunlong, LÜ Hongzhi, CUI Yunjiang, et al. Method for fracture effectiveness evaluation based on 3D Mohr Circle and its application[J]. Acta Petrolei Sinica, 2018, 39(5): 564-569. doi: 10.7623/syxb201805007 |
| [20] |
KUSTER G T, TOKSÖ Z M N. Velocity and attenuation of seismic waves in two-phase media:Part Ⅱ. Experimental results[J]. Geophysics, 1974, 39(5): 607-618. doi: 10.1190/1.1440451 |
| [21] |
NORRIS A N. A differential scheme for the effective moduli of composites[J]. Mechanics of Materials, 1985, 4(1): 1-16. doi: 10.1016/0167-6636(85)90002-X |
| [22] |
BERRYMAN J G. Long-wavelength propagation in composite elastic media Ⅱ. ellipsoidal inclusions[J]. The Journal of the Acoustical Society of America, 1980, 68(6): 1820-1831. doi: 10.1121/1.385171 |
| [23] |
HASHIN Z, SHTRIKMAN S. A variational approach to the theoty of the elastic behavior multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127-140. doi: 10.1016/0022-5096(63)90060-7 |
| [24] |
葛瑞·马沃可, 塔潘·木克基, 杰克·德沃金. 岩石物理手册:孔隙介质中地震分析工具[M]. 合肥: 中国科学技术大学出版社, 2008. MAVKO G, MUKERJI T P, DVORIKIN J. The rock physics handbook:Tools for seismic analysis in porous media[M]. Cambridge University Press, 2008. |
| [25] |
邓运华, 彭文绪. 渤海锦州25-1S混合花岗岩潜山大油气田的发现[J]. 中国海上油气, 2009, 21(3): 145-150, 156. DENG Yunhua, PENG Wenxu. Discovering large buriedhill oil and gas fields of migmatitic granite on Jinzhou 25-1S in Bohai Sea[J]. China Offshore Oil and Gas, 2009, 21(3): 145-150, 156. doi: 10.3969/j.issn.1673——1506.2009.03.001 |
 2019, Vol. 41
2019, Vol. 41


