2. 中国石油塔里木油田分公司, 新疆 库尔勒 841000
2. Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
硫化物应力腐蚀开裂(Sulfide Stress Corrosion Cracking,简称SSCC)和应力腐蚀开裂(Stress Corrosion Cracking,简称SCC)是油气田金属材料腐蚀的一种严重失效形式,是各种腐蚀行为中破坏性最大的一种,常常在没有任何预兆的情况下突然发生,造成灾难性的事故[1-4]。随着超深、超高压高温井的不断开发,这些苛刻井中的服役环境迫切需要使用高强度耐蚀石油管材,如不锈钢、镍基合金和钛合金完井管柱等。因此,对硫化物应力腐蚀开裂的研究是目前需要解决的课题之一,而C型环正是一种用于测定各种金属应力腐蚀破裂敏感性的用途广泛且经济的试样,适用于多种产品形式,特别适用于石油行业的输送管道和完井管柱的实验。
目前,有不少国内外学者开展了大量的C型环应力腐蚀开裂的实验研究[3-10]和有限元应力计算的理论研究[11-14]。Thomson等用增强铁素体不锈钢的C型环试样开展了纵向和横向的应力腐蚀开裂(SCC)的实验研究[15]。Bandeira等[16],按NACE TM0177标准[17],加载75%
在NACE TM 0177[17]和国标GB/T 15970.5《金属和合金的腐蚀—应力腐蚀实验》中均颁布有关C型环实验应力的加载挠度(位移)的计算公式[21],但没有给出加载载荷与应力的计算公式。因此,本文基于材料力学理论,针对管道横向应力腐蚀开裂,对任意C型环试样结构尺寸及其力学关系,建立了C型环内任意截面的力学模型,推导出了其外壁和内壁任意一点环向应力与C型环试样加载位移、加载载荷之间的理论计算公式,同时,建立了其有限元力学模型,用有限元法对本文推导的理论公式进行了对比分析和验证,结果表明,本文推导的理论公式是正确的,为C型环实验加载位移和加载载荷的计算提供了理论公式。
1 C型环内外壁任意点环向应力与加载载荷的理论公式推导C型环结构及其加载受力示意图如图 1所示,假设在螺栓位置
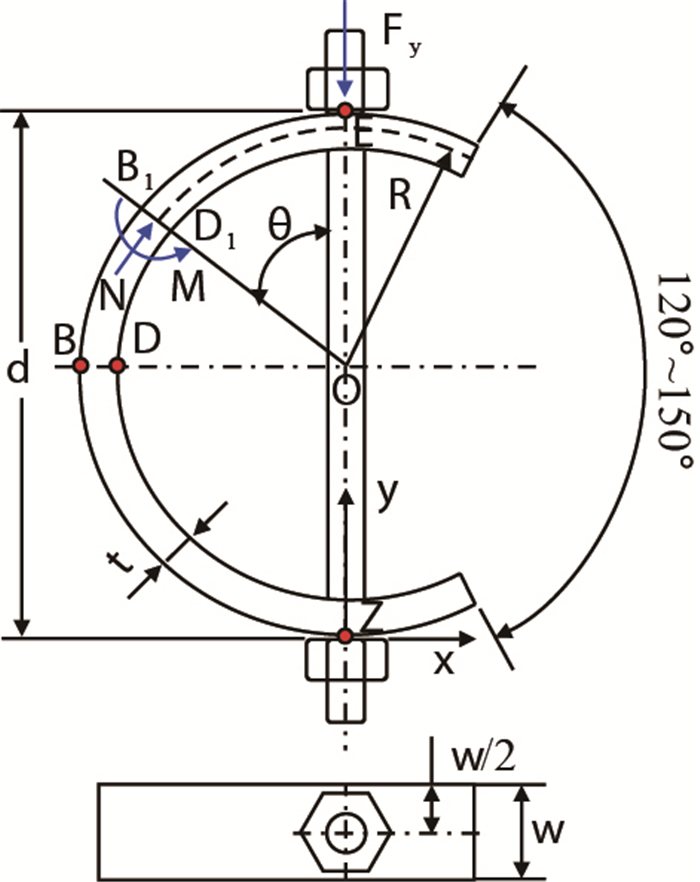 |
| 图1 C型环加载及受力示意图 Fig. 1 C-ring loading and loading diagram |
根据材料力学,曲梁在外载荷作用下,横截面上同时存在弯矩
| $ \sigma {\rm{ = }}\sigma {}_1 \pm {\sigma _2}{\rm{ = }}\dfrac{N}{A} \pm \dfrac{{My}}{{\rho S}} $ | (1) |
在任意
| $ \left\{ \begin{array}{l} N = - {F_{\rm{y}}}\sin \theta {\rm{ }}\\ M = {F_{\rm{y}}}R\sin \theta \\ A = wt, {\rm{ }}S = wt\left( {R - r} \right)\\ R{\rm{ = }}(d - t)/2 \end{array} \right. $ | (2) |
| $ {\rm{ }}{\rho _{{\mathop{\rm o}\nolimits} }} = \dfrac{d}{2}, {\rm{ }}{y_{{\mathop{\rm o}\nolimits} }} = \dfrac{d}{2} - r $ | (3) |
| $ {\rho _{{\mathop{\rm i}\nolimits} }} = \dfrac{d}{2} - t, {\rm{ }}{y_{{\mathop{\rm i}\nolimits} }} = r - \left( {\dfrac{d}{2} - t} \right){\rm{ }} $ | (4) |
式中:
式(3)和式(4)分别为C型环外壁和内壁处的应力计算参数位置。将式(2)
| $ {\sigma _{{{\rm o}} }}{\rm{ = }}\dfrac{{{F_{\rm{y}}}\sin \theta }}{w} {\dfrac{{2r}}{{d\left( {d - t - 2r} \right)}}} $ | (5) |
| $ {\sigma _{\rm{i}}}{\rm{ = }} - \dfrac{{{F_{\rm{y}}}\sin \theta }}{{wt}}\left[ {\dfrac{{\left( {d - t} \right)\left( {2r - d + 2t} \right)}}{{(d - 2t)\left( {d - t - 2r} \right)}} + 1} \right] $ | (6) |
该C型环为矩形截面,其中,性层曲率半径
| $ {{r = }}\dfrac{t}{{\ln {\dfrac{d}{{d - 2t}}} }} $ | (7) |
式(5)和式(6)中,当
在图 1中
| $ {U_{\rm{y}}} = \dfrac{3}{4}\dfrac{{{\rm{\pi }} {F_{\rm{y}}}{{\left( {d - t} \right)}^3}}}{{Ew{t^3}}} $ | (8) |
| $ {U_{\rm{y}}} = \dfrac{{{\rm{\pi }} d\left( {d - t} \right)}}{{4tE}}{\sigma _{\rm{B}}} $ | (9) |
式中:
标准NACE TM 0177中对C型环试样给出了要求,宽度与厚度比
由式(8)可得C型环加载载荷与加载处的位移变化关系式为式(10)。当
| $ {F_{\rm{y}}} = \dfrac{{4wE}}{{3{\rm{\pi }} {{\left( {\dfrac{d}{t} - 1} \right)}^3}}}{U_{\rm{y}}} $ | (10) |
| $ {F_{\rm{y}}} = \dfrac{{2tEwd(d - t - 2r)}}{{{\rm{\pi }} dr(d - t)}}{U_{\rm{y}}} $ | (11) |
将式(9)代入式(10)和式(11),可推导出C型环外壁
| $ {F_{\rm{y}}} = \dfrac{{dw}}{{3{{\left( {\dfrac{d}{t} - 1} \right)}^2}}}{\sigma _{\rm{B}}} $ | (12) |
| $ {F_{\rm{y}}} = \dfrac{{{w}d\left( {d - t - 2r} \right)}}{{2r}}{\sigma _{\rm{B}}} $ | (13) |
前面推导的理论公式(5)
根据C型环试样结构可知,属于平面应力带厚度的力学问题,本研究将开展外径为88.9 mm的13Cr-110油管结构的C型环应力分析研究,该油管有3种壁厚的结构尺寸,如表 1所示,其宽度按NACE TM 0177标准[17]取5倍的壁厚尺寸。根据图 1中C型环的标准结构,可建立其有限元力学模型,如图 2所示。在C型环的
| 表1 C型环结构尺寸 Tab. 1 C-ring structure dimensions |
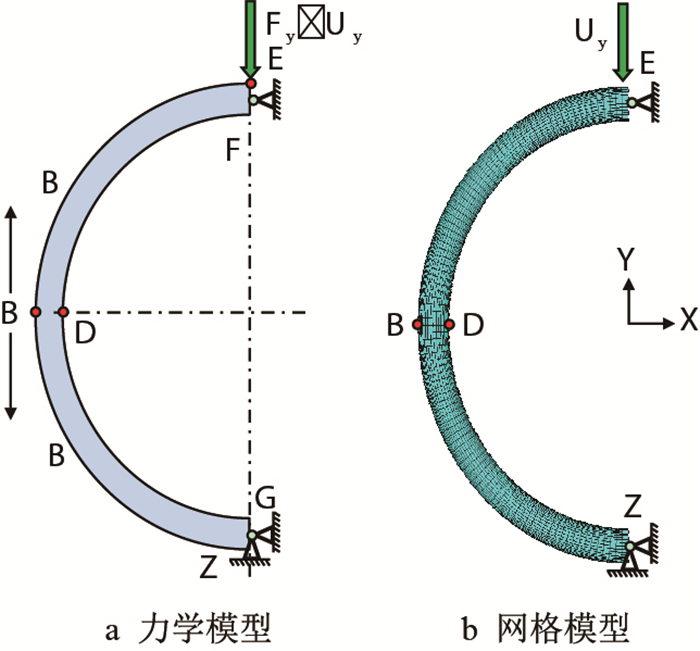 |
| 图2 C型环试样有限元力学模型 Fig. 2 Finite-element mechanical model of C-ring |
C型环13Cr-110油管材料的弹性模量为2.1
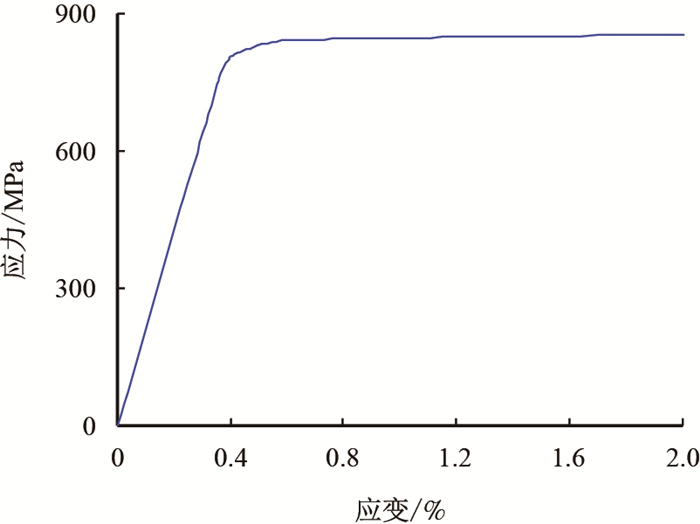 |
| 图3 13Cr-110油管材料应力-应变曲线 Fig. 3 Stress-strain curve of 13Cr-110 tubing material |
加载过程:首先,在图 2中
图 4为理论公式计算和有限元计算的加载载荷
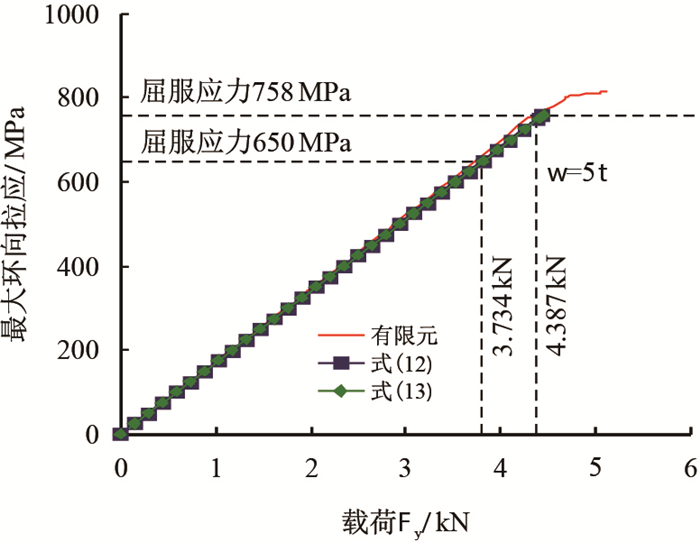 |
| 图4 最大环向拉应力随加载载荷的变化关系 Fig. 4 The relationship between maximum circumferential tensile stress and load |
从图 4可知,理论式(12)
从图 4中有限元计算结果可知,当
|
表2 加载位移 |
|
表3 加载载荷 |
图 5为3种壁厚C型环的最大环向拉应力随加载位移变化关系的有限元法和理论公式(9)的计算结果对比曲线,从图 5中的曲线可知,在弹性范围内,理论公式的曲线结果与有限元法的计算结果非常吻合,即在弹性范围内可直接使用理论公式(9)计算
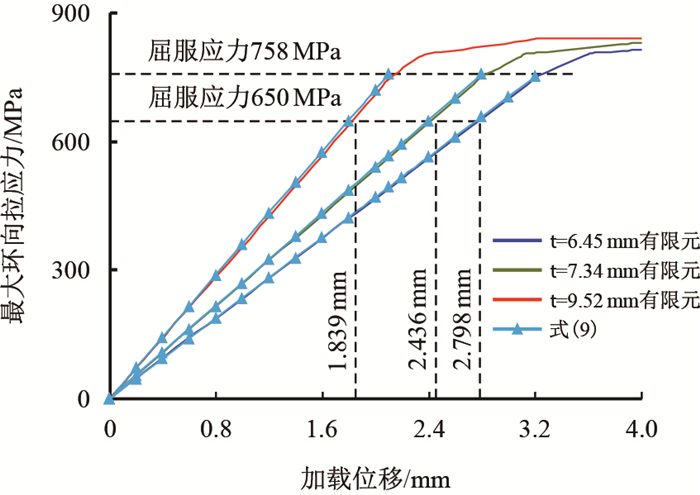 |
| 图5 最大环向拉应力随加载位移的变化关系 Fig. 5 The relationship between maximum circumferential tensile stress and loading displacement |
图 5中可知,对于3种不同的壁厚,要在
最大环向应力
从表 3中可知,3种壁厚加载载荷的理论公式计算结果相对于有限元法的计算结果比较,其误差的绝对值:理论公式(12)误差1.0%
根据本文建立的C型环试样的有限元计算模型,首先在力学模型图 2中
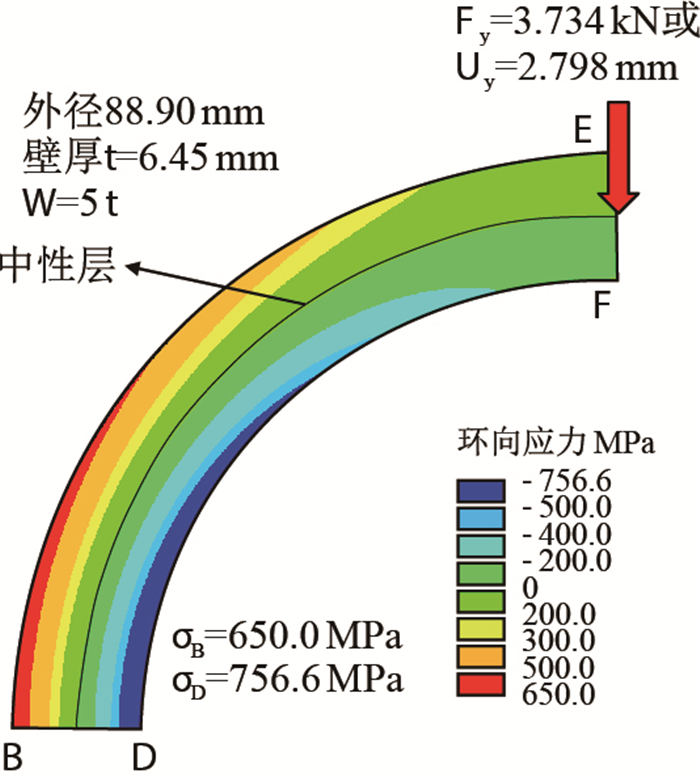 |
| 图6 环向应力等值线分布云图 Fig. 6 The von mises stress contours of circumferential stresses |
|
表4 最大环向拉应力和压应力计算结果( |
从表 4中可知,C型环外壁拉应力理论公式(5)和其内壁压应力理论公式计算结果与有限元法的计算结果误差分别为2.14%和1.65%,即理论公式的结果和有限元结果较吻合,误差较小,说明理论公式的推导是正确的。
从图 6中可见,C型环试样内部存在明显的中性层,即应力为0的位置,中性层以上为环向拉应力,中性层以下为环向压应力,从图 6可知其拉应力为0
 |
|
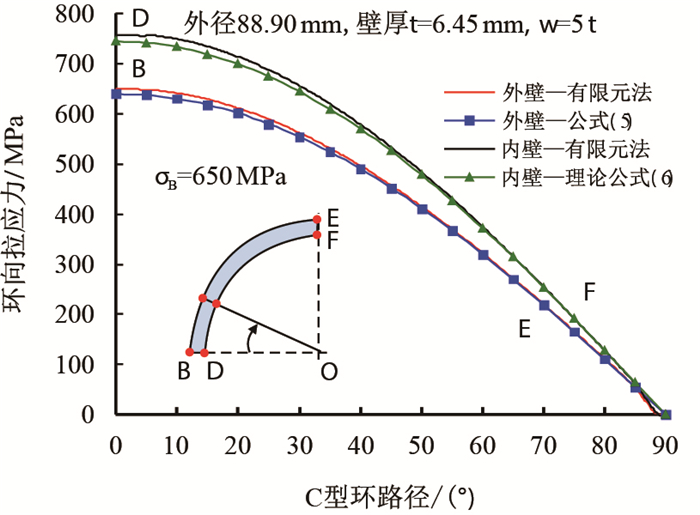
图7
C环内外壁环向应力沿 |
图 7为有限元法和理论公式计算出的C型环内外壁环向应力沿
从图 7中可知,其内外壁的环向应力沿
(1) 根据C型环试样结构及其受力关系,推导出了其外壁和内壁任意一点环向应力与试样加载位移、加载载荷之间的理论计算公式,式(5)、式(12)及式(13)为C型环硫化氢应力开裂和应力腐蚀开裂实验加载参数确定提供了简便的计算方法。
(2) 当C型环试样最大环向拉应力为650 MPa时,用有限元法计算出需要施加的载荷3.734 kN,用本文式(12)和式(13)计算出施加的载荷分别为3.802和3.816 kN,其相对有限元法的误差分别为-1.82%和-2.2%,说明推导的理论公式可靠。
(3) C型环内壁最大压应力的绝对值始终比外壁最大环向拉应力高,因此在确定外壁最大环向拉应力的应力腐蚀开裂实验前时,建议用式(6)计算其内壁的最大环向压应力,并判断其是否超过该材料的屈服应力,为合理确定外壁最大环向拉应力提供理论数据。
| [1] |
卢志明, 何凯伦, 霍培栋, 等. 316L焊缝与304母材C型环试样应力腐蚀敏感性研究[J]. 浙江工业大学学报, 2017, 45(3): 270-273, 299. LU Zhiming, HE Kailun, HUO Peidong, et al. Research on stress corrosion sensitivity of 316L weld joint and 304 base metal C-ring specimen[J]. Journalo of Zhejiang University of Technology, 2017, 45(3): 270-273, 299. doi: 10.3969/j.issn.1006-4303.2017.03.007 |
| [2] |
薛艳, 赵密锋, 吕祥鸿, 等. 不锈钢管应力腐蚀开裂的评价方法[J]. 腐蚀与防护, 2018, 39(5): 340-343. XUE Yan, ZHAO Mifeng, LÜ Xianghong, et al. Stress corrosion cracking evaluation methods of stainless steel tubing[J]. Corrosion & Protection, 2018, 39(5): 340-343. doi: 10.11973/fsyfh-201805004 |
| [3] |
杨世洲, 李春福, 李辉, 等. 2205双相不锈钢在酸性H2S环境下的应力腐蚀行为及开裂机理[J]. 稀有金属材料与工程, 2018, 47(3): 904-909. YANG Shizhou, LI Chunfu, LI Hui, et al. Stress corrosion behavior and cracking mechanism of 2205 duplex stainless steel in acidic H2S environment[J]. Rare Metal Materials and Engineering, 2018, 47(3): 904-909. |
| [4] |
赵华莱, 姜放, 李珣, 等. C型环试验的加载应力计算[J]. 天然气与石油, 2007, 25(2): 21-24, 32. ZHAO Hualai, JIANG Fang, LI Xun, et al. Loading stress calculation in C type ring test[J]. Natural Gas and Oil, 2007, 25(2): 21-24, 32. doi: 10.3969/j.issn.1006-5539.-2007.02.007 |
| [5] |
BAI Tao, CHEN Peng, GUAN Kaishu. Evaluation of stress corrosion cracking susceptibility of stainless steel 304 L with surface nanocrystalization by small punch test[J]. Materials Science & Engineering:A, 2013, 561: 498-506. doi: 10.1016/j.msea.2012.10.071 |
| [6] |
LEE S J, CHANG Y S. Evaluation of primary water stress corrosion cracking growth rates by using the extended finite element method[J]. Nuclear Engineering and Technology, 2015, 47(7): 895-906. doi: 10.1016/j.net.2015.08.-003 |
| [7] |
陆峰, 张晓云, 汤智慧, 等. 复合材料对LY12CZ铝合金C-环应力腐蚀性能的影响[J]. 材料工程, 2003(7): 3-6. LU Feng, ZHANG Xiaoyun, TANG Zhihui, et al. Effect of composite materials on the C-ring stress corrosion cracking of LY12CZ aluminum alloy[J]. Journal of Materials Engineering, 2003(7): 3-6. doi: 10.3969/j.issn.1001-4381.2003.07.001 |
| [8] |
但晨, 蔡力勋, 包陈, 等. 用于断裂韧度测试的C形环小试样的规则化方法与应用[J]. 机械工程学报, 2015, 51(14): 54-65. DAN Chen, CAI Lixun, BAO Chen, et al. Normalization method used to determine fracture toughness with Cring small size specimen and its application[J]. Journal of Mechanical Engineering, 2015, 51(14): 54-65. doi: 10.3901/JME.2015.14.054 |
| [9] |
张晓云, 孙志华, 刘明辉, 等. 环境对高强度铝合金应力腐蚀行为的影响[J]. 中国腐蚀与防护学报, 2007, 27(6): 354-362. ZHANG Xiaoyun, SUN Zhihua, LIU Minghui, et al. Influence of different environments on stress corrosion cracking of high strength aluminum alloys[J]. Journal of Chinese Society for Corrosion and Protection, 2007, 27(6): 354-362. doi: 10.3969/j.issn.1005-4537.2007.06.008 |
| [10] |
王鹏.高温高压井油管完井液导致应力腐蚀开裂分析[C]//北京: 全国失效分析学术会议论文集, 2015: 4. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGVE201510001048.htm
|
| [11] |
谢尘, 黎军顽, 封源, 等. C型环试样淬火及深冷处理应力演变的数值研究[J]. 材料热处理学报, 2015, 36(增2): 248-255. XIE Chen, LI Junwan, FENG Yuan, et al. Numerical simulation of stress evolution in C-ring specimen during quenching and deep cryogenic treatment[J]. Transactions of Materials and Heat Treatment, 2015, 36(S2): 248-255. |
| [12] |
金骥戎, 宋仁国, 祁星, 等. 阴极极化对7050铝合金C-环应力腐蚀敏感性的影响[J]. 腐蚀科学与防腐技术, 2015, 27(3): 249-253. JIN Jirong, SONG Renguo, QI Xing, et al. Effect of cathodic polarization on susceptibility to SCC of C-ring specimens in 7050 aluminum alloy[J]. Corrosion Science and Protection Technology, 2015, 27(3): 249-253. doi: 10.11903/1002.6495.2014.224 |
| [13] |
姚小飞, 谢发勤, 吴向清, 等. 温度对超级13Cr油管钢慢拉伸应力腐蚀开裂的影响[J]. 石油矿场机械, 2012, 41(9): 50-53. YAO Xiaofei, XIE Faqin, WU Xiangqing, et al. Effects of temperature on the slow strain rate tension stress corrosion cracking of super 13Cr tubing steel[J]. Oil Field Equipment, 2012, 41(9): 50-53. doi: 10.3969/j.issn.1001-3482.-2012.09.012 |
| [14] |
但晨, 蔡力勋, 包陈. C形环小试样疲劳裂纹扩展试验方法与应用[J]. 工程力学, 2015, 32(12): 27-32. DAN Chen, CAI Lixun, BAO Chen. Test method and application of fatigue crack propagation with C-ring specimen[J]. Engineering Mechanics, 2015, 32(12): 27-32. doi: 10.6052/j.issn.1000-4750.2014.05.0412 |
| [15] |
THOMSON J K, PAWEL S J. A comparison of the C-ring test and the jones test as standard practice test methods for studying stress corrosion cracking in ferritic steels[C]. SPE 2015-5670, 2015.
|
| [16] |
MERLIN C E B, ANDRÉF V A B. Adaptation of nace standard TM 0177 C-ring test for flexible pipes carcass[C]. NACE International Corrosion 2013 Conference & EXPO. NACE-2013-2680, 1-10.
|
| [17] |
NACE Standard. Laboratory testing of metals for resistance to sulfide stress cracking and stress corrosion cracking in H2S environments[S]. TM 01772005, 2005.
|
| [18] |
姚小飞, 谢发勤, 吴向清, 等. Cl-浓度对超级13Cr油管钢应力腐蚀开裂行为的影响[J]. 材料导报B:研究篇, 2012, 26(9): 38-41, 45. YAO Xiaofei, XIE Faqin, WU Xiangqing, et al. Effects of Cl- concentration on stress corrosion cracking behaviors of super 13Cr tubing steels[J]. Materials Review, 2012, 26(9): 38-41, 45. doi: 10.3969/j.issn.1005-023X.2012.-18.011 |
| [19] |
朱敏, 刘智勇, 杜翠薇, 等. X65和X80管线钢在高pH值溶液中的应力腐蚀开裂行为及机理[J]. 金属学报, 2013, 49(12): 1590-1596. ZHU Min, LIU Zhiyong, DU Cuiwei, et al. Stress corrosion cracking behavior and mechanism of X65 and X80 pipeline steels in high pH solution[J]. Acta Metallurgica Sinica, 2013, 49(12): 1590-1596. doi: 10.3724/SP.J.1037.-2013.00315 |
| [20] |
周伟民. 13Cr和super13Cr不锈在CO2饱和的CaCl2完井液中的应力腐蚀开裂[D].武汉: 华中科技大学, 2007. ZHOU Weimin. The SCC of 13Cr and super 13Cr stainless steel in CO2-saturated CaCl2 completion brine[D]. Wuhan:Huazhong University of Science and Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10487-2009036363.htm |
| [21] |
上海核工程研究设计院. GB/T15970.51998金属和合金的腐蚀、应力腐蚀试验, 第五部分: C型环试样的制备和应用[S].北京: 中国标准出版社, 1998.
|
| [22] |
刘鸿文. 材料力学[M]. 北京: 人民出版社, 1980.
|
 2019, Vol. 41
2019, Vol. 41


