2. 成都理工大学能源学院, 四川 成都 610059;
3. 昆山利通天然气有限公司, 江苏 昆山 215300;
4. 重庆页岩气勘探开发有限责任公司, 重庆 渝中 404100;
5. 乐山市燃气有限公司, 四川 乐山 614000
2. Energy School, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
3. Kunshan Litong Natural Gas Co. Ltd., Kunshan, Jiangsu 215300, China;
4. Chongqing Shale Gas Exploration and Development Co. Ltd., Yuzhong, Chongqing 404100, China;
5. Leshan Gas Co. Ltd., Leshan, Sichuan 614000, China
天然气管道运行优化的目标是在保证最大输量的前提下使得包括压缩机站在内的整个管线系统能耗最小,而这两者往往不能同时实现,因为更大的输气量需要更高的压力,而获得更高的压力则需要消耗更多的压缩机能耗,同时也会造成更大的运行噪声[1-3]。在长距离天然气管道运行费用中,压缩机站的运行费用是主要支出,以往的研究表明,所有压缩机的能耗占管道总能耗的25%~50%[4-5]。而本文则是针对输量确定的情况,对大型天然气长输管道能耗进行优化,以达到整个管线能耗最低的目的,确定能耗最低且安全可靠的运行方案。
1968年,PETER开始以最低能耗为目标函数并利用动态规划法求解天然气管道运行优化模型[6]。在近几十年中,国内外专家学者对天然气管道运行优化模型进行了大量的研究。
(1) 目标函数:在天然气管道运行优化中,常常以输气量最大[7]、管线充填量最大[8-9]、管线能耗最低[10-11]等为目标函数,而应用最为广泛的则是能耗最低优化模型。
(2) 约束条件:不等式约束用于限制指定范围内的管道流量、压力和温度[10-11];等式约束主要表示管道内气体流动的控制方程,包括质量平衡方程、压力方程和温度方程[11];压缩机约束最初是基于理想压缩机假设而建立的,并未与实际工况结合,而LIU Enbin等建立了一套包括喘振曲线和滞止曲线在内的多项式来描述离心压缩机的可行域[10-12],得到符合压缩机实际运行状况的约束条件。除了压缩机的运行参数外,压缩机的运行状态(开或关)也是需要优化的一个重要参数,尤其是对于含有较多压缩机的管道系统[13]。
(3)优化变量:通常包括各节点的压力、温度、各单元(管道、压缩机)的流量、各压缩机的状态和功率,其中压力、流量和压缩机功率为连续变量,压缩机状态为离散变量[14]。
虽然专家学者们经过长时间的研究,已经能采用多种优化算法求解天然气管道优化运行的相关数学模型,但动态规划法因其保证全局最优且容易处理非线性问题的优势成为求解管道运行优化问题最成功的算法[15-17]。然而,对于利用动态规划法求解含压缩机站数量多的大型天然气长输管线能耗模型的研究仍稍显不足,而本文则是针对大型天然气长输管段管线距离长、设置压缩机站较多、压缩机数量大的特点,在管道实际运行情况下,运用动态规划法快速求解,制定出优化运行方案,为管道的经济运行提供参考和指导。
1 模型建立与求解 1.1 模型建立 1.1.1 目标函数以各压缩机站的压缩机能耗之和最低为目标函数,各压缩机之间天然气流量均分。
| $ {\rm{min }}F = {\rm{min }}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{f_i}} } \left( {{k_{ij}}, {Q_{ij}}, {p_{{\rm{d}}i}}} \right) $ | (1) |
式中:
各压缩机站的能耗主要为压缩机运行能耗,因此压缩机的运行状态直接决定目标函数值即总能耗值,故将天然气管道压缩机站出站压力及压缩机开关状态确定为优化变量,如式(2)所示。
| $ X = \left( {{p_{{\rm{d}}i}}, {k_{ij}}} \right) $ | (2) |
(1) 流量约束
天然气管道中的流量必须满足某个节点最小、最大流量的约束。即
| $ {Q_{i{\rm{ min}}}} \leqslant {Q_i} \leqslant {Q_{i{\rm{ max}}}}{\rm{ }}, i = 1, 2, \cdot \cdot \cdot , {N_n} $ | (3) |
式中:
(2) 压力约束
管道节点的压力应满足如下约束
| $ {p_{i{\rm{ min}}}} \leqslant {p_i} \leqslant {p_{i{\rm{ max}}}}{\rm{ }}, i = 1, 2, \cdot \cdot \cdot , {N_n} $ | (4) |
式中:
(3) 管道强度约束
为了保证管道的安全运行,第
| $ {p_k} \leqslant {p_{k{\rm{ max}}}}{\rm{ }}, k = 1, 2, \cdot \cdot \cdot , {N_{\rm{p}}} $ | (5) |
式中:
(4) 流量平衡约束
根据质量守恒定律,在管道任意节点,都应满足流入该节点的天然气质量等于流出该节点的天然气质量。
| $ \sum\limits_{\scriptstyle k \in {\boldsymbol{R}_i}\atop \scriptstyle i = 1}^{N_n} {{\alpha _{ik}}} {M_{ik}} + {Q_i} = 0 $ | (6) |
式中:
(5) 压缩机功率约束
压缩机功率方程为
| $ N = \dfrac{{MH}}{\eta } $ | (7) |
式中:
压缩机能头曲线根据下式计算
| $ - H = {h_1}{S^2} + {h_2}SQ + {h_3}{Q^2} $ | (8) |
式中:
压缩机效率曲线根据下式计算
| $ \dfrac{{ - H}}{\eta } = {e_1}{S^2} + {e_2}SQ $ | (9) |
式中:
压缩机喘振曲线根据下式计算
| $ {Q_{\rm{g}}} = {s_1} + {s_2}H $ | (10) |
式中:
压缩机滞止曲线根据下式计算
| $ {Q_{\rm{t}}} = {s_3} + {s_4}H $ | (11) |
式中:
根据式(7)
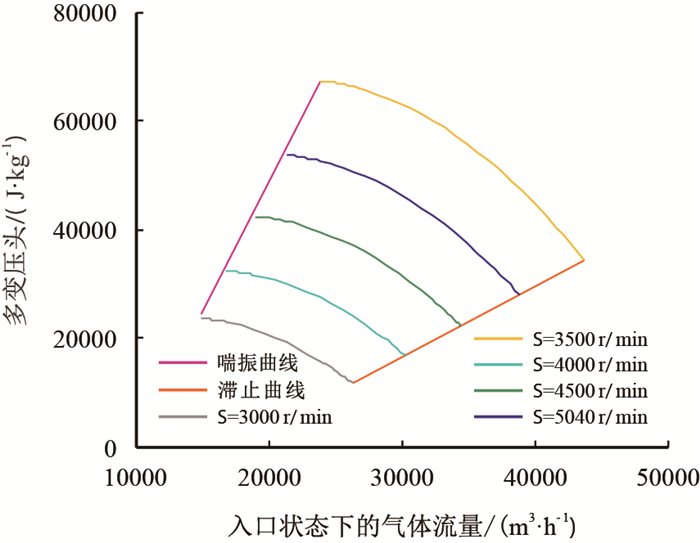 |
| 图1 压缩机压头特性曲线图 Fig. 1 Compressor head characteristic curve |
(6) 压缩机功率约束
压缩机在运行过程中应满足如下功率约束
| $ {N_{j{\rm{ min}}}}\leqslant {N_j} \leqslant{N_{j{\rm{ max}}}}{\rm{ }}, j = 1, 2, \cdot \cdot \cdot , {N_{\rm{c}}} $ | (12) |
式中:
(7) 压缩机出口温度限制
压缩机出口温度即压缩机站出站温度不应超过如下温度约束
| $ {T_{\rm{d}}} \leqslant{T_{{\rm{d}}\max }} $ | (13) |
式中:
动态规划是管道优化中最重要的解决方案之一,随着计算机技术的进步,动态规划得到了迅速的发展。本文创新性地将动态规划应用于天然气长距离输气管道运行优化,这是以往研究中所没有的。
1.2.1 动态规划法的应用把某一输气管道沿途的分气支线简化为分气点后,这条管道的运行过程就可视为一个多阶段过程,从而可以用动态规划算法对全线的压缩机站进行优化,如图 2所示。
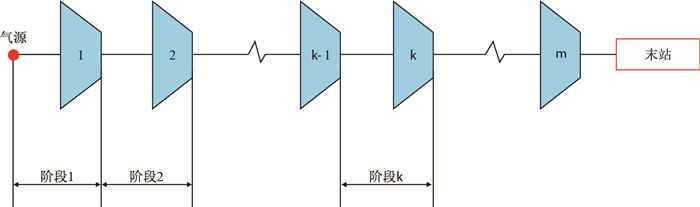 |
| 图2 动态规划阶段示意图 Fig. 2 Schematic of dynamic programming stage |
设压缩机站数为
状态变量
| $ {x_k} = {p_{{\rm{d}}, k - 1}}, k=2\sim m+1 $ | (14) |
决策变量
| $ {d_k} = {\varepsilon _k}, k=1\sim m $ | (15) |
状态演变方程
| $ {x_{k + 1}} = {T_k}\left( {{x_k}, {d_k}} \right), k=1\sim m $ | (16) |
阶段效应
| $ {V_k} = {C_k}\left( {{x_{k + 1}}, {d_k}} \right), k=1\sim m $ | (17) |
目标函数
| $ {V_{1, k}}\left[ {{x_{k\!+\!1}}, {p_{1, k}}\left( {{x_{k\!+\!1}}} \right)} \right]\!\!=\!\!\sum\limits_{i\!=\!1}^k {{C_i}} \left( {{x_{i\!+\!1}}, {d_i}} \right), k\!=\!1\sim m $ | (18) |
最优目标函数
| $ {f_k}\left(\!{{x_{k\!+\!1}}}\!\right)\!=\!\mathop {{\rm{min}}}\limits_{{p_{1, k}}\left(\!{{x_{k\!+\!1}}}\!\right)} {\rm{ }}{V_{1, k}}\left[\!{{x_{k\!+\!1}}, {p_{1, k}}\left(\!{{x_{k\!+\!1}}}\!\right)} \right], k=1\sim m $ | (19) |
函数递推方程
| $ {f_k}\left(\!{{x_{k\!+\!1}}}\!\right)\!\!=\!\mathop {{\rm{min}}}\limits_{{d_k} \in D_k^y\left(\!{{x_{k\!+\!1}}}\!\right)} \left[\!{{f_{k\!-\!1}}\left(\! {{x_k}}\!\right)\!+\!{C_k}\left(\!{{x_{k\!+\!1}}, {d_k}}\!\right)} \right], k=1\sim m $ | (20) |
初始条件
| $ {x_1} = {p_{{\rm{d}}, 0}} $ | (21) |
| $ {f_0}\left( {{x_1}} \right) = 0 $ | (22) |
式中:
采用动态规划法求解所建优化模型的计算过程主要包含4部分:(1)确定所有站的状态空间和决策变量;(2)根据管道的水力计算、热力计算进行站间递推;(3)确定所有决策变量对应的压缩机能耗进行站内递推;(4)对整个方案进行算法回溯确定最优运行方案。整个寻优过程的计算框图如图 3所示。
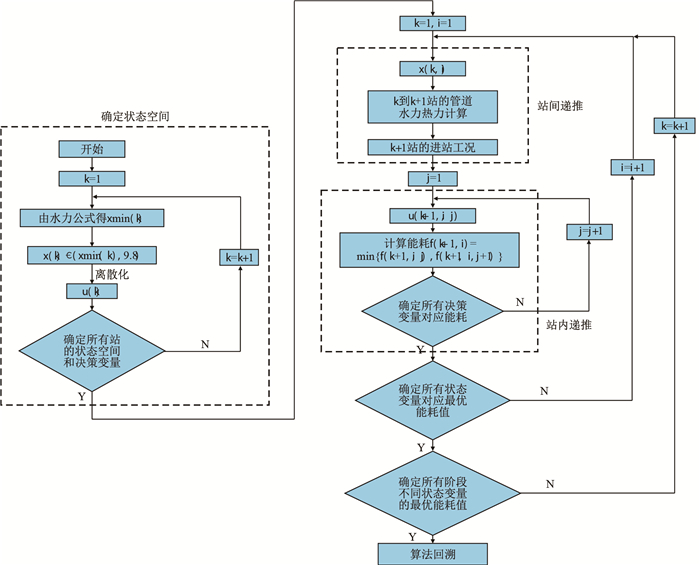 |
| 图3 管道优化动态规划算法框图 Fig. 3 Flow chart of the pipeline operation optimization dynamic programming algorithm |
管线全长3 840 km,管道设计输量170
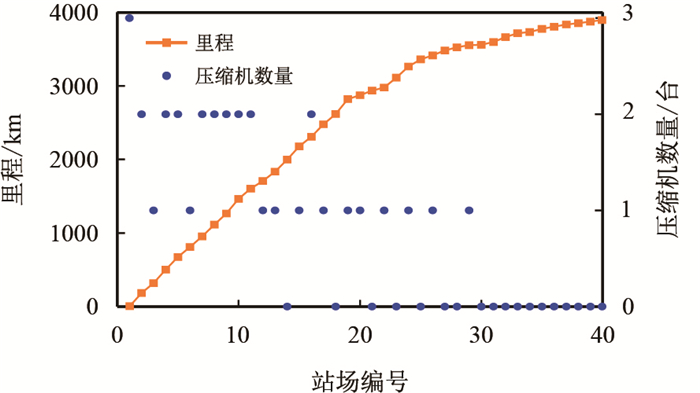 |
| 图4 各站里程及压缩机配置数量 Fig. 4 Length of pipe between each compressor station and number of compressors in each station |
本文将离心压缩机的压头曲线、压头/效率曲线、喘振流量曲线、滞止流量曲线、转速和流量曲线与现场实际运行数据进行拟合。部分站场压缩机的曲线系数如表 1所示。
| 表1 压缩机特性曲线拟合系数 Tab. 1 Compressor characteristic curve coefficients |
算例各压缩机站注入量和分输量如图 5所示,其中,站场1、15、22、26、32注入天然气,站场14、18、21、23
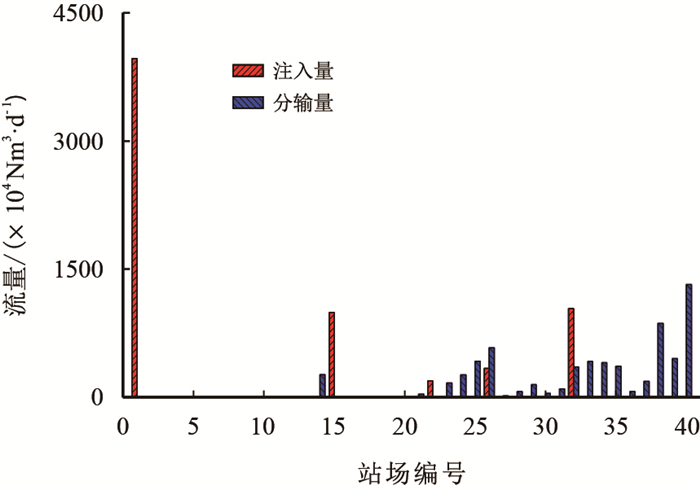 |
| 图5 各站注入量和分输量 Fig. 5 Multipoint injection volume and distribution volume |
将模型求解所得的优化结果与算例运行日报表对比,以体现本文模型及优化算法的正确性和可行性。
2.1.1 运行日报表方案(实际运行方案)根据现场运行报表,得到算例的各站运行参数如表 2所示。
| 表2 算例各站场运行日报表 Tab. 2 Daily operation report of each compressor station in the case |
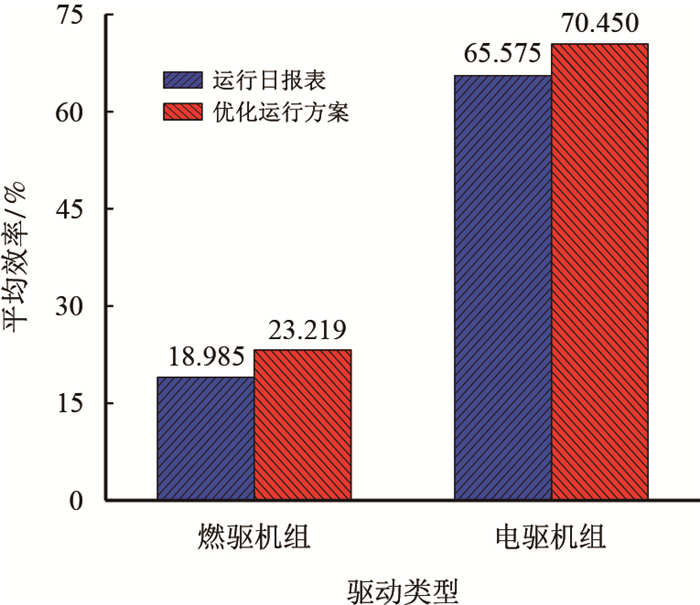
从表 2可以看出,在实际运行方案,压缩机总开机台数为23台,除压气站12之外,其余压缩机站都处于开机状态,其中,仅首站1和压气站16开启两台压缩机。对于使用燃气轮机驱动的压缩机站,其机组效率是指燃气轮机和压缩机的综合效率;对于使用电驱驱动机的压缩机站,其机组效率是指电驱驱动机和压缩机的综合效率。燃气轮机机组的平均效率为21.09%,电驱机组的平均效率为65.58%,总压降为44.67 MPa,总功率为245 495.4 kW,实际运行状况能耗较高,压降较大,机组效率较低,还有很大的优化空间。
2.1.2 优化运行方案经过优化方法计算,得到优化运行方案如表 3所示。
| 表3 算例优化运行方案 Tab. 3 Optimized operation scheme of the case |
优化运行方案中,压气站4、压气站8和压气站12关机,压气站3、7、10、11、15、16、17、19、20共计9个压缩机站以管道设计压力9.8 MPa作为出站压力。
现将运行日报表和优化运行方案的压缩机开机台数、各站进出站压力、功率、沿程压降进行比较,如表 4和图 6
| 表4 运行日报表与优化方案压缩机开机台数对比 Tab. 4 Comparison of the numbers of starting-up compressors between daily operation report and optimized operation scheme |
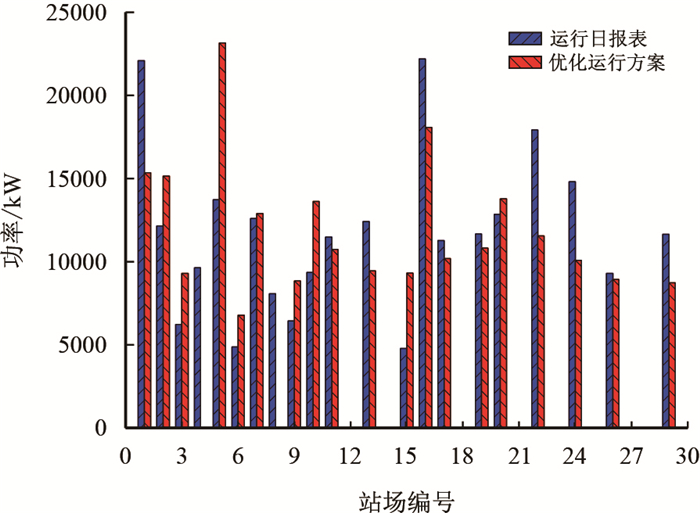 |
| 图6 运行日报表与优化方案功率对比图 Fig. 6 Power comparison between actual operation and optimized operation |
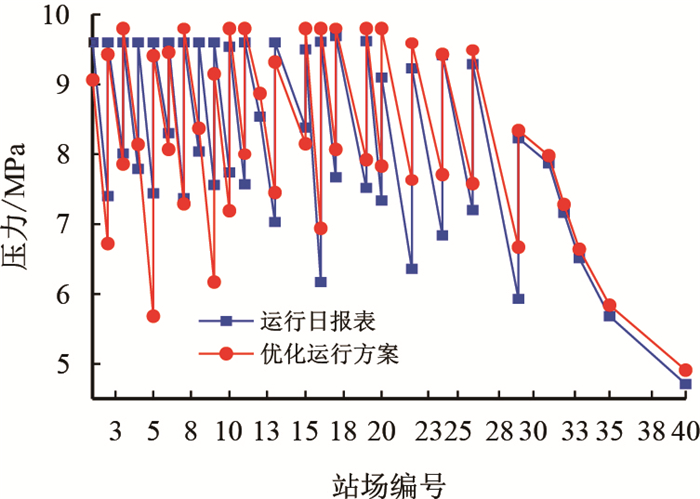 |
| 图7 运行日报表与优化运行方案的进出站压力对比图 Fig. 7 Comparison of inlet and outlet pressures |
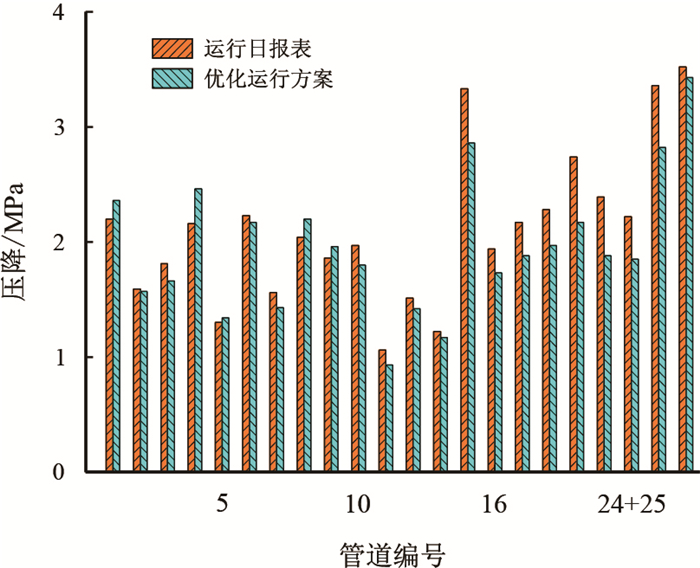 |
| 图8 运行日报表与优化运行方案各管段压降对比图 Fig. 8 Comparison of pressure drops between daily operation report and optimized operation scheme |
 |
| 图9 运行日报表与优化运行方案的平均效率对比图 Fig. 9 Comparison of average efficiency between daily operation report and optimization operation scheme |
实际运行方案中压缩机总开机台数为23台,优化运行方案中总开机台数为25台,其中,优化方案在站场2、站场5、站场7、站场9、站场10中均增加了一台压缩机,在站场1、站场4、站场8均减少了一台压缩机。
运行日报表中总功率为245 495.4 kW,优化方案总功率为226 775.1 kW,功率减少18 720.3 kW,降低了7.6%,其中,站场1、站场4、站场8、站场13、站场16、站场22、站场24、站场29功率下降较多,优化结果明显。
经过优化过后,站场1、站场3、站场5、站场6、站场9、站场13出站压力均有所下降,站场4、站场8、站场11、站场12、站场13、站场16、站场17、站场19、站场20、站场22、站场24、站场26、站场29进站压力均有所提高(站场5由于越站进站压力较低),从而降低了压缩机能耗。
实际运行方案中管线总压降为46.46 MPa,优化方案中管线总压降为43.06 MPa,压降降低了3.40 MPa。其中,管段3、7、10、12、15、16、17+18、20+21、22+23、24+25、26+27+28压降降低较多。
经过优化,各站场驱动机组的效率得到了显著提高。除站场11外,其他站场燃气驱动机组效率提高到23%以上,电机驱动机组效率提高到70%以上。燃气驱动机组平均效率提高了4.234%,电力驱动机组平均效率提高了4.875%,可显著降低能耗。
由图 9可以看出,优化方案对部分压缩机站的压缩机开机数量、压气站进出口压力等进行了优化。站间平均压力较高,大部分管段压降较小。实际运行方案总压降为46.46 MPa,优化方案总压降为43.06 MPa。优化方案的总压降明显低于实际运行方案,证明了模型和求解方法的可行性和有效性。
2.2 优化运行方案能耗测算与比较为了比较分析管道的能耗,采用式(23)和式(24)计算管道的能耗和燃气消耗,采用式(25)将其转换为标准煤消耗,结果如表 5所示。
| 表5 能耗指标对比图 Tab. 5 Comparison chart of energy consumption indicators |
根据《综合能耗计算通则》(GB/T 2589—2008),利用各项指标来评价分析管道能耗。
其中,耗气量
| $ {W_{\rm{g}}} = \sum\limits_{i = 1}^n {\dfrac{{{N_i}{t_i}}}{{{n_{{\rm{g}}i}}}}} g_{\rm{e}} $ | (23) |
| $ {W_{\rm{e}}} = \sum\limits_{i = 1}^n {\dfrac{{{N_i}{t_i}}}{{{n_{{\rm{e}}i}}}}} $ | (24) |
因此,总能耗可用式(25)计算
| $ F = \dfrac{{{W_{\rm{g}}}{\omega _1} + {W_{\rm{e}}}{\omega _2}}}{{{T_{\rm{ur}}}}} $ | (25) |
式中:
表 5直观地反映了优化后各能耗指标均有所降低,验证了优化模型的可行性和有效性。
优化方案和运行日报表相比,总的耗气量减少了527.45
近年来,国内外专家学者对于动态规划法的研究进展如表 6所示,从表中可以看出,1968年PETER首先开始使用动态规划的方法来求解小型天然气管道运行优化模型。多年来,越来越多的专家开始采用动态规划法来优化输气管道的能耗,但其中的一个局限是管道规模太小(压缩机站少,压缩机数量少)。
| 表6 动态规划法研究进展 Tab. 6 Research progress of dynamic programming |
此外,一些学者忽略压缩机的实际运行情况,仅通过数学方法处理压缩机方程,与压缩机实际工况相差较大。在前辈的基础上,使用动态规划法优化大型天然气管道的能耗,同时根据北京油气调控中心在线测试软件测得的实际数据对压缩机曲线进行修正和拟合,得到符合工程实际的压缩机描述方法,这与之前仅仅通过简单的数学方法处理压缩机曲线方程而忽略压缩机实际运行情况相比更具有先进性与实用价值。而本文的研究对象管道总长3 840 km,管道设计年输量170
(1) 提出了一种以能耗最低为目标函数的天然气管道运行优化模型,同时将这个模型应用于大型天然气管道(管道全长3 840 km,管道设计能力170
(2) 比较优化运行方案和实际运行方案的管道压降和运行能耗可得:采用优化运行方案,管道压降降低了3.4 MPa,燃气轮机机组的平均效率增加了4.234%,电驱机组的平均效率增加了4.875%,功率下降了18 720.38 kW,生产能耗下降了8.65%。
(3) 根据实际运行方案和优化运行方案对比,优化运行方案可大幅降低全线能耗,具有巨大的经济效益,可应用于工程实践。
| [1] |
LIU Enbin, PENG Shanbi, YANG Tiaowei. Noise silencing technology for upright venting pipe jet noise[J]. Advances in Mechanical Engineering, 2018, 10(8): 1-15. doi: 10.1177/1687814018794819 |
| [2] |
LIU Enbin, YAN Shikui, PENG Shanbi, et al. Noise silencing technology for manifold flow noise based on ANSYS fluent[J]. Journal of Natural Gas Science and Engineering, 2016, 29(2): 322-328. doi: 10.1016/j.jngse.2016.01.021 |
| [3] |
LIU Enbin, YAN Shikui, WANG Di, et al. Large eddy simulation and fw-h acoustic analogy of flow-induced noise in elbow pipe[J]. Journal of Computational and Theoretical Nanoscience, 2016, 12(9): 2866-2873. doi: 10.1166/jctn.2015.4191 |
| [4] |
PENG Shanbi, LIU Enbin, XIAN Weiwei, et al. Dynamic simulation of an underground gas storage injectionproduction network[J]. Journal of Environmental Biology, 2015, 36(4): 799-806. |
| [5] |
PETER J W, ROBERT E L. Optimization of naturalgas pipeline systems via dynamic programming[J]. IEEE Transactions on Automatic Control, 1968, 13(5): 475-481. doi: 10.1109/TAC.1968.1098990 |
| [6] |
KASHANI A H A, MOLAEI R. Techno-economical and environmental optimization of natural gas net-work operation[J]. Chemical Engineering Research and Design, 2014, 92(11): 2106-2122. doi: 10.1016/j.cherd.2014.02.006 |
| [7] |
CHI K S, VARANON U, CHRISTINE W C, et al. An integrated expert system/operations research approach for the optimization of natural gas pipeline operations[J]. Engineering Applications of Artificial Intelligence, 2000, 13(4): 465-475. doi: 10.1016/s0952-1976(00)00022-1 |
| [8] |
USTER H, DILAVEROGLU S. Optimization for design and operation of natural gas transmission networks[J]. Applied Energy, 2014, 133: 56-69. doi: 10.1016/j.apenergy.-2014.06.042 |
| [9] |
TABKHI F, PIBOULEAU L, HERNANDEZ-RODRIGUEZ G, et al. Improving the performance of natural gas pipeline networks fuel consumption minimization problems[J]. Aiche Journal, 2010, 56(4): 946-964. doi: 10.1002/aic.12011 |
| [10] |
LIU Enbin, LI Changjun, YANG Yi. Optimal energy consumption analysis of natural gas pipeline[J]. The Scientific World Journal, 2014, 2014: 1-8. doi: 10.1155/2014/506138 |
| [11] |
LIU Enbin, LÜ Liuxin, MA Qian, et al. Steady-state optimization operation of the west-east gas pipeline[J]. Advances in Mechanical Engineering, 2019, 11(1): 1-14. |
| [12] |
WU Suming, RÍOS-MERCADO R Z, BOYD E A, et al. Model relaxations for the fuel cost minimization of steady-state gas pipeline networks[J]. Mathematical and Computer Modelling, 2000, 31(2-3): 197-220. doi: 10.1016/S0895-7177(99)00232-0 |
| [13] |
LIU Enbin, LI Changjun, YANG Liuting, et al. Research on the optimal energy consumption of oil pipeline[J]. Journal of Environmental Biology, 2015, 36(4): 703-711. |
| [14] |
ROGER Z R, CONRADO B S. Optimization problems in natural gas transportation systems:A state-of-the-art review[J]. Applied Energy, 2015, 147: 536-555. doi: 10.1016/j.apenergy.2015.03.017 |
| [15] |
ZHANG Xiaorui, WU Changchun, ZUO Lili. Minimizing fuel consumption of a gas pipeline in transient states by dynamic programming[J]. Journal of Natural Gas Science and Engineering, 2016, 28: 193-203. doi: 10.1016/j.-jngse.2015.11.035 |
| [16] |
GAO Xianwen, LIU Tan, YUAN Qingyun, et al. A novel optimization approach for oil and gas production process considering model parameters uncertainties[J]. The Canadian Journal of Chemical Engineering, 2016, 94(9): 1710-1722. doi: 10.1002/cjce.22560 |
| [17] |
HEMANT S L, PETER B P. A dynamic programming based gas pipeline optimizer[J]. Analysis and Optimization of Systes, 1990, 144: 123-132. doi: 10.1007/BFb0120035 |
| [18] |
高松竹.输气干线压缩机站运行优化研究[D].成都: 西南石油学院, 2003. GAO Songzhu. Study on operation optimization of compressor station in gas transmission line[D]. Chengdu:Southwest Petroleum Institute, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10615-2003051411.htm |
| [19] |
DANILOVIC D, MARICIC V K, RISTOVIC I. Determination of optimal parameters of distributive gas pipeline by dynamic programming method[J]. Petroleum Science and Technology, 2011, 29(9): 924-932. doi: 10.1080/10916460903468443 |
| [20] |
张俊, 李博, 柳建军, 等. 输气管道运行优化算法适性研究[J]. 计算机仿真, 2016, 33(1): 369-372. ZHANG Jun, LI Bo, LIU Jianjun, et al. Adaptability of algorithms in natural gas pipeline operation optimization problem[J]. Computer Simulation, 2016, 33(1): 369-372. doi: 10.3969/j.issn.1006-9348.2016.01.080 |
| [21] |
HESAM A B, BOOZARJOMEHRY R B. Dynamic optimization of natural gas networks under customer demand uncertainties[J]. Energy, 2017, 134: 968-983. doi: 10.1016/j.energy.2017.06.087 |
| [22] |
杜培恩, 陈新果, 李欣泽, 等. 基于动态规划法与改进遗传算法的管网稳态运行优化[J]. 油气储运, 2018, 37(3): 285-290. DU Peien, CHEN Xinguo, LI Xinze, et al. Steadystate operation optimization of pipeline network based on dynamic programming method and advanced genetic algorithm[J]. Oil & Gas Storage and Transportation, 2018, 37(3): 285-290. doi: 10.6047/j.issn.1000-8241.2018.03.-008 |
 2019, Vol. 41
2019, Vol. 41


