射孔作为主要的完井方式之一,是套管井连接储层和井筒的唯一通道,对沟通储层、解除近井带污染、释放产能尤为重要[1-5]。射孔参数的合理设计是保障射孔作业效果的关键所在,目前关于射孔参数的选取和设计方法主要是基于射孔表皮计算的参数敏感性分析,依据不同孔密或孔径下穿深对产能比的影响分析进行参数设计[6-11]。研究发现,孔密、孔径、穿深和相位等射孔参数主要影响的是射孔表皮,其中对敏感性分析曲线形态起决定性作用的是平面流效应表皮[4, 7, 12-13],而平面流效应表皮模型是关于穿深的对数函数,根据对数函数的性质,随着穿深的增加,产能比会不断增大,表现出穿深越深对于产能释放越有利的结论。实际上,该结论不符合大家关于射孔穿深超过一定深度后对产能贡献极小的研究认识[2, 8-9],现有方法无法有效设计射孔最佳穿深参数。分析原因在于,现有射孔表皮计算模型未有效考虑射孔孔道流动摩阻的影响[4, 7, 14-15],无法准确表征射孔穿深和产能关系。因此,亟需建立基于孔道流动摩阻分析的最佳射孔穿深确定新方法,进一步优化射孔参数设计,对加强套管井产能建设具有重要意义。
1 研究基础 1.1 射孔参数设计方法现状目前,射孔参数的设计主要基于不同孔径或孔密下穿深对产能比的影响敏感性分析结果[1-4],如图 1,图 2所示。
 |
| 图1 不同孔径下穿深对产能的影响 Fig. 1 The influence of the perforation penetration under different perforation diameter |
 |
| 图2 不同孔密下穿深对产能的影响 Fig. 2 The influence of the perforation penetration under different perforation density |
敏感性分析的关键在于表皮计算,目前常用的表皮主要有射孔表皮、钻井污染表皮、井斜表皮和打开不完善表皮等[6-13]。其中,对于一口既定的油井,井斜角和打开程度为定值,即井斜表皮和打开不完善表皮为一定值。同时,钻井作业结束后钻井表皮也是一定值,与射孔穿深的关系不大。因此,射孔井随着射孔穿深变化的表皮主要为射孔表皮。
研究表明,射孔表皮包括平面流效应表皮、垂向汇聚流表皮、井筒效应表皮和压实带表皮几类[4, 7],垂向汇聚流表皮、井筒效应表皮和压实带表皮均为大于0的正值,即会对储层造成伤害,唯一仅有平面流效应表皮,如式(1)、式(2)所示,随着穿深的变化,可能成为负表皮。
| $ {{S}_{\rm H}}=\ln \dfrac{{{r}_{\rm w}}}{{{r}_{\rm we}}} $ | (1) |
| $ {r_{{\rm{we}}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{4}{L_{\rm{p}}}, {\kern 50pt}\theta = {0^\circ}}\\ {{\alpha _\theta }\left( {{r_{\rm{w}}} + {L_{\rm{p}}}} \right), {\kern 15pt}\theta \ne {0^\circ}} \end{array}} \right. $ | (2) |
式中:
分析发现,影响参数敏感性分析曲线形态的主要表皮系数为平面流效应表皮,但由式(1)可知,平面流效应表皮模型为对数函数,因此当把射孔穿深无限增加后,参数敏感性分析的曲线形态会随着穿深的增加一直增加,即使计算到12 000 mm深度,产能比同样呈类似线性曲线上升趋势(图 3,图 4)。该结论明显不符合实际情况:当射孔穿深达到某一阀限值时,穿深对于产能的贡献较小,因此存在一个最佳射孔穿深[2, 8-9]。
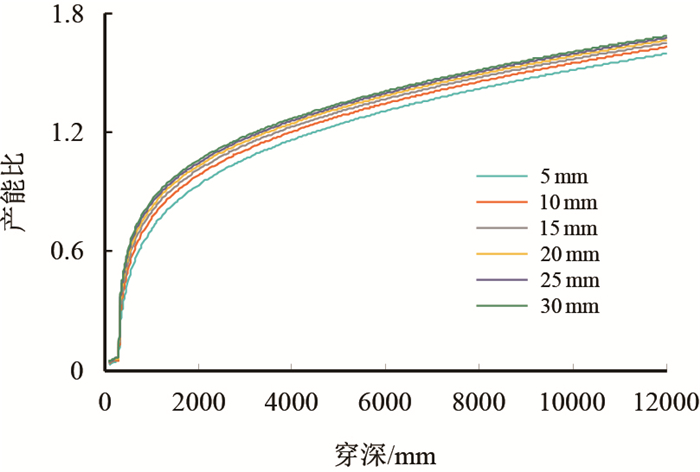 |
| 图3 不同孔径下产能比随穿深变化趋势 Fig. 3 The change trend of PRI by perforation penetration under different perforation diameter |
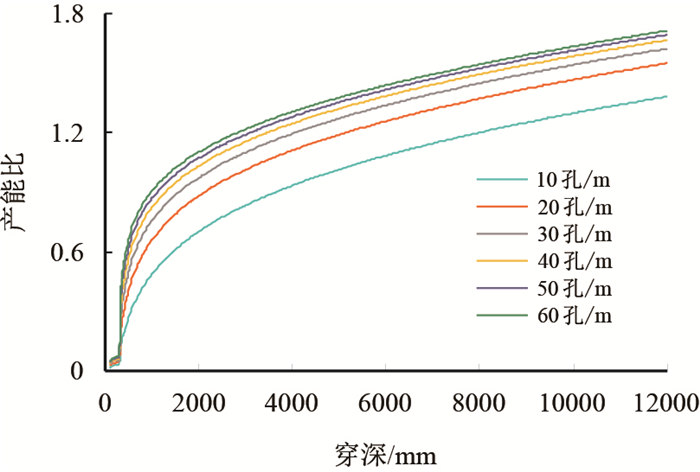 |
| 图4 不同孔密下产能比随穿深变化趋势 Fig. 4 The change trend of PRI by perforation penetration under different perforation density |
由上述分析可知,现有射孔表皮模型无法准确解释穿深和产能之间关系,依据该表皮模型的参数敏感性分析结果无法确定最优射孔穿深,为射孔参数的设计带来困扰。产生上述现象的原因在于,现有射孔表皮模型未考虑射孔孔眼流动摩阻的影响。因此,亟需通过理论创新,研究建立基于孔道流动摩阻分析的最佳射孔穿深确定新方法,为最佳射孔穿深的设计提供理论依据。
2 模型描述 2.1 油藏内流动将单个射孔孔道等效为一个微观角度上的水平井裸眼水平段[14-19],油藏到射孔孔道的流动可用如下方程描述[20-22]
| $ {{q}_{\rm s}}\left( x \right)={{J}_{\rm s}}\left[ {{p}_{\rm e}}-{{p}_{\rm w}}\left( x \right) \right] $ | (3) |
式中:
类比单位长度水平井采油指数方程[23-24],可得射孔段采油指数为
| $ {{J}_{\rm s}}=\dfrac{0.543\sqrt{{{K}_{\rm h}}{{K}_{\rm v}}}}{{{\mu }_{\rm o}}{{B}_{\rm o}}}\cdot \dfrac{1}{\ln \dfrac{4\beta {{h}_{\rm o}}}{{\rm{\pi }} {{r}_{\rm w}}}+\ln \left( \tan\dfrac{{\rm{\pi }} {{Z}_{\rm w}}}{2{{h}_{\rm o}}} \right)} $ | (4) |
式中:
假定射孔孔道内流体为单相紊流流动[21, 25],流入孔道的流体呈均匀流动,孔道渗流的物理模型如图 5所示。
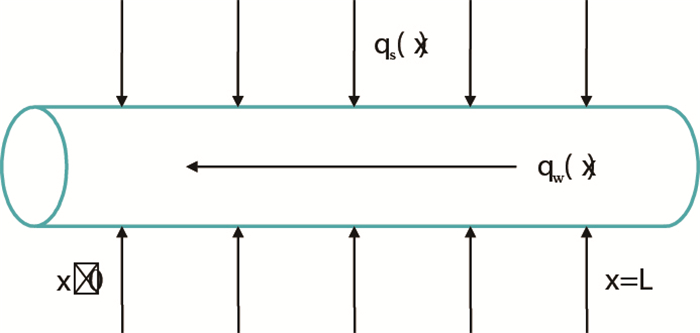 |
| 图5 油藏与射孔孔道耦合流动示意图 Fig. 5 The coupling flow diagram of reservoir and perforation tunnel |
依据上述流动模型,采用体积平衡方法耦合油藏内流动和射孔孔道内流动,可得
| $ \dfrac{{\rm d}\left[ {{q}_{\rm w}}\left( x \right) \right]}{{\rm d}x}=-{{q}_{\rm s}}\left( x \right) $ | (5) |
式中:
从射孔孔道角度而言,可将射孔孔道看作为无限外边界油藏中的水平井,因此存在如下边界条件
| $ \lim\limits_{x\to \infty }\, {{p}_{\rm w}}\left( x \right)={{p}_{\rm e}} $ | (6) |
| $ \lim\limits_{x\to 0 }\, {{p}_{\rm w}}\left( x \right)={{p}_{\rm wf}} $ | (7) |
式中:
式(6)、式(7)可做如下等效变换
| $ \lim\limits_{x\to \infty }\, \dfrac{{{q}_{\rm w}}\left( x \right)}{{\rm d}x}=0 $ | (8) |
| $ \lim\limits_{x\to \infty }\, \dfrac{{{q}_{\rm w}}\left( x \right)}{{\rm d}x}=-{{J}_{\rm s}}\Delta p=-{{J}_{\rm s}}({{p}_{\rm e}}-{{p}_{\rm wf}})=-C $ | (9) |
式中:
射孔后整个射孔段打开采油,该情况等效类似于裸眼完井、割缝衬管或割缝筛管完井的水平井[21, 26-27]。因此,射孔孔道内压力梯度方程为
| $ \dfrac{{\rm d}{{p}_{\rm w}}\left( x \right)}{{\rm d}\left( x/d \right)}=1.34\times {{10}^{-13}}\times 4f\dfrac{{{\rho }_{\rm o}}v_{x}^{2}}{2} $ | (10) |
式中:
式(10)可变形为
| $ \dfrac{{\rm d}{{p}_{\rm w}}\left( x \right)}{{\rm d}x}=1.086\times {{10}^{-13}}\times 4f\dfrac{{{\rho }_{\rm o}}q_{\rm w}^{2}\left( x \right)}{{{d}^{5}}} $ | (11) |
依据Dikken对水平段内摩擦阻力损失的研究,认为在完全紊流区对于某一确定孔眼工况的摩擦系数为一个常数[28]
| $ 4f=\dfrac{1}{4{{\lg }^{2}}\left( \varepsilon /3.7d \right)} $ | (12) |
式中:
分别对式(3)和式(5)求导,可得
| $ \dfrac{{\rm d}\left[ {{q}_{\rm s}}\left( x \right) \right]}{{\rm d}x}+{{J}_{\rm s}}\dfrac{{\rm d}\left[ {{p}_{\rm w}}\left( x \right) \right]}{{\rm d}x}=0 $ | (13) |
| $ \dfrac{{{\rm d}^{2}}\left[ {{q}_{\rm w}}\left( x \right) \right]}{{\rm d}{{x}^{2}}}+\dfrac{{\rm d}\left[ {{q}_{\rm s}}\left( x \right) \right]}{{\rm d}x}=0 $ | (14) |
由式(13)和式(14),可得
| $ \dfrac{{{\rm d}^{2}}\left[ {{q}_{\rm w}}\left( x \right) \right]}{{\rm d}{{x}^{2}}}-{{J}_{\rm s}}\dfrac{{\rm d}\left[ {{p}_{\rm w}}\left( x \right) \right]}{{\rm d}x}=0 $ | (15) |
将式(11)、式(12)代入式(15),并令
| $ \lambda =\dfrac{2.715\times {{10}^{-14}}{{\rho }_{\rm o}}}{{{d}^{5}}{{\lg }^{2}}\left( \varepsilon /3.7d \right)} $ | (16) |
可得
| $ \dfrac{{{\rm d}^{2}}\left[ {{q}_{\rm w}}\left( x \right) \right]}{{\rm d}{{x}^{2}}}-\lambda {{J}_{\rm s}}q_{\rm w}^{2}\left( x \right)=0 $ | (17) |
应用边界条件式(8),式(9),可计算得到射孔长度趋于无穷大时的解析解
| $ q_{\rm w}^{{}}\left( x \right)={{\left[ \sqrt{\dfrac{\lambda {{J}_{\rm s}}}{6}}x+{{\left( \sqrt{\dfrac{3}{2\lambda {{J}_{\rm s}}}}C \right)}^{-1/3}} \right]}^{-2}} $ | (18) |
式(18)中
| $ {{Q}_{\rm o}}={{q}_{\rm w}}\left( 0 \right)-{{q}_{\rm w}}\left( L \right) $ | (19) |
式中:
若不考虑流体在射孔孔道内流动时流动摩阻的影响,则射孔孔道的产量随射孔孔道的穿深呈线性增加,此时的产量为
| $ {{Q}_{\rm o}}^{\prime }={{J}_{\rm s}}L\Delta p $ | (20) |
式中:
采用上述模型,依据Dikken关于最优长度的优化原则即可确定射孔孔道的最佳长度[21, 23, 28]。该优化原则定义最优长度是当射孔孔道流动摩擦损失减少了20%产能时的长度,即
| $ {{{{{Q}_{\rm o}}}/{{{Q}_{\rm o}}}}^{\prime }}=0.8 $ | (21) |
按照上式进行求解计算,即可得到Dikken优化原则下的最优射孔穿深。
3 基于最优穿深分析的参数优化基于流动摩阻分析的最佳射孔穿深确定,建立射孔参数优化设计新方法(图 6),具体流程如下。
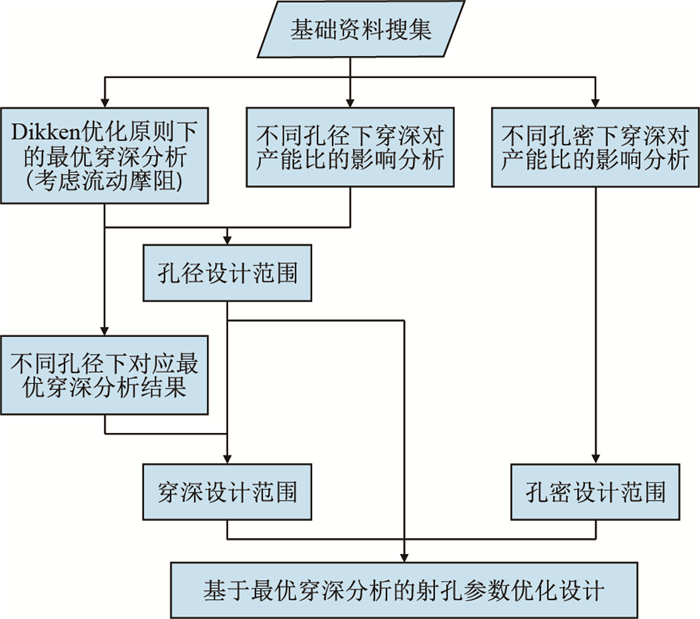 |
| 图6 基于最优穿深分析的射孔参数优化设计新方法 Fig. 6 The new method of perforation parameter optimization based on depth perforation analysis |
(1) 采用上述最佳射孔穿深确定方法,绘制不同孔径条件下产量与射孔穿深的变化曲线图(记为图A),确定不同孔径下对应的最佳射孔穿深;
(2) 按照式(22)分析不同孔径或不同孔密下穿深对产能比的影响敏感性,并作图,分别记为图B、图C。
| $ R_{\rm PRI}=\dfrac{\ln \left( {{{r}_{\rm e}}}/{{{r}_{\rm w}}}\; \right)}{\ln \left( {{{r}_{\rm e}}}/{{{r}_{\rm w}}}\; \right)+{{S}_{\rm t}}} $ | (22) |
式中:
(3) 由图A和图B综合分析,观察曲线分布趋势和密集程度,首先确定射孔孔径大小。在此基础上,结合第一步结果,确定最佳射孔穿深。
(4) 观察不同孔密下穿深对产能比的影响敏感性趋势(图C),确定射孔孔密参数范围。
(5) 优化设计得到的射孔参数范围是参数低限,以此为依据优选符合参数范围的射孔弹,确保射孔效果。
4 实例分析以某一区块馆陶组储层定向井射孔参数设计为例,该区块定向井均为9
| 表1 某区块馆陶组储层基础参数 Tab. 1 The reservoir basic parameter of Guantao Formation |
由表 1参数,按照基于最优穿深分析的射孔参数优化设计新方法,作出不同孔径下产能和射孔穿深的关系曲线,如图 7所示,并确定不同孔径所对应的最优穿深。同时,采用传统的分析方法作出不同孔径和不同孔密条件下射孔穿深对产能比的影响敏感性分析图,如图 8,图 9所示。
 |
| 图7 馆陶组储层Dikken优化原则下的最佳射孔穿深 Fig. 7 The optimal perforation depth analysis diagram based on the principle of Dikken |
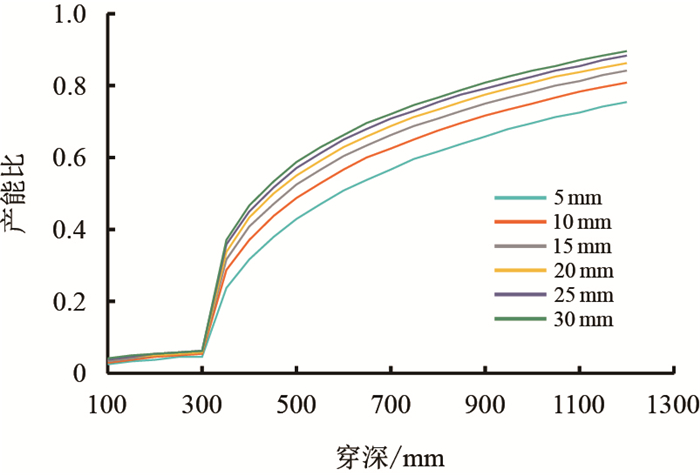 |
| 图8 不同孔径下穿深对产能的影响敏感性 Fig. 8 The sensitivity of perforation depth under different perforation diameter |
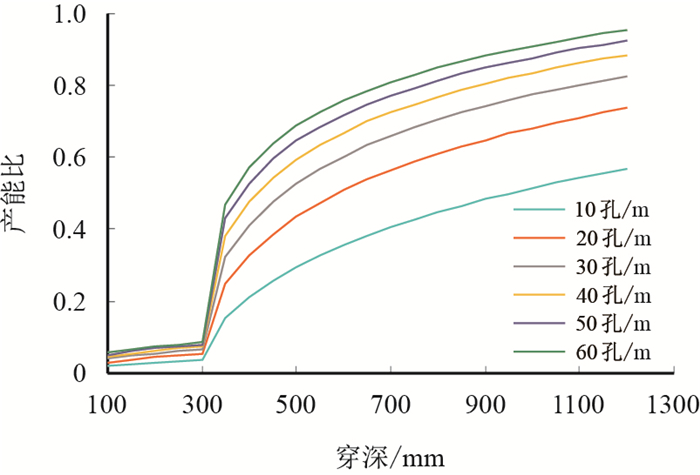 |
| 图9 不同孔密下穿深对产能的影响敏感性 Fig. 9 The sensitivity of perforation penetration under different perforation density |
采用上述最优射孔穿深确定新方法,设计馆陶组储层射孔参数范围。由图 7、图 8可知,孔径由小到大,曲线分布密集程度由稀疏到密集变化,当孔径大于20 mm时,进一步增大孔径,对于产能的影响较小,因此确定射孔孔径需大于20 mm;确定射孔孔径后,由图 7可知,20 mm孔径对应最优穿深最低为600 mm,因此设计射孔穿深
由图 9可知,和射孔孔径设计类似,孔密由低到高,曲线分布逐渐密集,设计射孔孔密40孔/m,对应射孔相位45°/135°。该区块馆陶组定向井优化设计后的射孔参数如表 2所示,建议选择大孔径射孔弹,该区块油井投产后单井产能达92.30 m
| 表2 某区块馆陶组储层射孔参数优化设计结果 Tab. 2 Perforation parameter optimization design results of Guantao Formation |
从设计结果来看,若单纯采用传统的设计方法,采用图 8、图 9难以对射孔穿深进行优化设计,因为从敏感性分析结果来看,产能比始终随着穿深的增加而快速增大。因此,研究形成的基于最优穿深分析的射孔参数优化设计新方法可为最优射孔穿深的设计提供理论依据。
5 结论(1) 针对射孔参数敏感性分析无法有效优化射孔穿深设计的问题,充分考虑射孔孔道流动摩阻的影响,研究建立了基于流动摩阻分析的最优射孔穿深设计新方法。
(2) 在最优穿深优化设计新方法研究基础上,综合考虑射孔表皮、钻井表皮、井斜表皮和打开不完善表皮模型,开展射孔参数敏感性分析,形成了射孔参数优化设计新思路。
(3) 实例分析表明,该方法可为最优射孔穿深的设计提供理论依据,有助于射孔参数的优化与设计。
| [1] |
万仁傅. 现代完井工程(第三版)[M]. 北京: 石油工业出版社, 2007. WAN Renfu. Advanced well completion engineering (the third edition)[M]. Beijing: Petroleum Industry Press, 2007. |
| [2] |
吴飞鹏, 蒲春生, 陈德春, 等. 射孔油井产能计算模型研究[J]. 石油钻探技术, 2008, 36(1): 69-72. WU Feipeng, PU Chunsheng, CHEN Dechun, et al. Productivity calculation model of perforated oil wells[J]. Petroleum Drilling Techniques, 2008, 36(1): 69-72. doi: 10.3969/j.issn.1001-0890.2008.01.019 |
| [3] |
李龙龙, 吴明录, 姚军, 等. 射孔水平井产能预测方法[J]. 油气地质与采收率, 2014, 21(2): 45-50. LI Longlong, WU Minglu, YAO Jun, et al. A new method to forecast the productivity of perforated horizontal well[J]. Petroleum Geology and Recovery Efficiency, 2014, 21(2): 45-50. doi: 10.3969/j.issn.1009-9603.2014.-02.013 |
| [4] |
熊友明, 潘迎德. 各种射孔系列完井方式下水平井产能预测研究[J]. 西南石油学院学报, 1996, 18(2): 56-62. XION Youming, PAN Yingde. Study on productivity prediction of the horizontal wells with completion methods of perforation series[J]. Journal of Southwest Petroleum Institute, 1996, 18(2): 56-62. |
| [5] |
姜伟, 倪满友. 渤海QK17-2大位移水平井TCP射孔技术实践[J]. 天然气工业, 2002, 22(5): 49-52. JIANG Wei, NI Manyou. Application of TCP technology in extended-reach horizontal Well-Bohai Sea QK17-2[J]. Natural Gas Industry, 2002, 22(5): 49-52. doi: 10.3321/j.issn:1000-0976.2002.05.013 |
| [6] |
潘迎德, 唐愉拉, 冯跃平. 射孔完井的产能预测及射孔参数优化设计[J]. 石油学报, 1991, 12(2): 61-71. PAN Yingde, TANG Yula, FENG Yueping. A prediction of the productivity in a perforated well and an optimization of the paramaters in perforation operation[J]. Acta Petrolei Sinica, 1991, 12(2): 61-71. doi: 10.7623/syxb199102008 |
| [7] |
陈勇光, 吴晓东, 安永生, 等. 各向异性油藏定向井射孔完井表皮因子模型研究[J]. 石油钻采工艺, 2009, 31(1): 42-46. CHEN Yongguang, WU Xiaodong, AN Yongsheng, et al. Research of skin factor model for perforated directional well in anisotropic reservoir[J]. Oil Drilling & Production Technology, 2009, 31(1): 42-46. doi: 10.3969/j.issn.1000-7393.2009.01.012 |
| [8] |
唐海军, 徐贵春, 段志刚, 等. 水平井射孔完井产能预测研究与应用[J]. 石油钻采工艺, 2010, 32(3): 27-32. TANG Haijun, XU Guichun, DUAN Zhigang, et al. Study on productivity prediction of horizontal wells perforation completion and its application[J]. Oil Drilling & Production Technology, 2010, 32(3): 27-32. doi: 10.3969/j.issn.-1000-7393.2010.03.007 |
| [9] |
安永生, 柳文莉, 祁香文. 射孔完井参数对水平井产量的影响[J]. 断块油气田, 2011, 18(4): 520-523. AN Yongsheng, LIU Wenli, QI Xiangwen. Influence of perforation parameter on productivity of horizontal well[J]. Fault-Block Oil & Gas Field, 2011, 18(4): 520-523. |
| [10] |
郭世慧, 王晓冬. 大斜度井两种计算产能和表皮系数方法的对比与讨论[J]. 油气井测试, 2008, 17(4): 21-23. GUO Shihui, WANG Xiaodong. The comparison and discussion on two methods of calculating deliverability and skin coefficient in slanted well[J]. Oil and Gas Well Testing, 2008, 17(4): 21-23. doi: 10.3969/j.issn.1004-4388.2008.04.008 |
| [11] |
祝金利, 李德海, 姜汉桥, 等. 影响水平井射孔完井产能的多因素分析[J]. 西南石油大学学报(自然科学版), 2008, 30(2): 97-100. ZHU Jinli, LI Dehai, JIANG Hanqiao, et al. Multi-factors analysis of influencing productivity of perforated horizontal well[J]. Journal of Southwes Petroleum University (Science & Technology Edition), 2008, 30(2): 97-100. doi: 10.3863/j.issn.1000-2634.2008.02.025 |
| [12] |
孙溪涛. 射孔孔眼表皮系数的计算与分析[J]. 测井技术, 2003, 27(增): 36-38. SUN Xitao. Calculation and analysis of perforating skin coefficient[J]. Well Logging Technology, 2003, 27(S): 36-38. doi: 10.3969/j.issn.1004-1338.2003.z1.011 |
| [13] |
陈元千, 阎为格. 表皮系数的分解方法[J]. 断块油气田, 2003, 10(6): 32-35. CHEN Yuanqian, YAN Weige. The decomposition method of the skin factor[J]. Fault-Block Oil & Gas Field, 2003, 10(6): 32-35. doi: 10.3969/j.issn.1005-8907.2003.06.011 |
| [14] |
范子菲, 方宏长, 俞国凡. 水平井水平段最优长度设计方法研究[J]. 石油学报, 1997, 18(1): 55-62. FAN Zifei, FANG Hongchang, YU Guofan. A sthudy on design method of optimal horizontal wellbore length[J]. Acta Petrolei Sinica, 1997, 18(1): 55-62. doi: 10.7623/-syxb199701010 |
| [15] |
胡月亭, 周煜辉, 苏义脑, 等. 水平井水平段长度优化设计方法[J]. 石油学报, 2000, 21(4): 80-86. HU Yueting, ZHOU Yuhui, SU Yinao, et al. Methods of optimal horizontal section length of a horizontal well[J]. Acta Petrolei Sinica, 2000, 21(4): 80-86. doi: 10.3321/j.issn:0253-2697.2000.04.015 |
| [16] |
符奇, 张烈辉, 胡书勇, 等. 底水油藏水平井水平段合理位置及长度的确定[J]. 石油钻采工艺, 2009, 31(1): 51-55. FU Qi, ZHANG Liehui, HU Shuyong, et al. Determination of optimum horizontal section location and length for horizontal wells in bottom water reservoir[J]. Oil Drilling & Production Technology, 2009, 31(1): 51-55. doi: 10.3969/j.issn.1000-7393.2009.01.014 |
| [17] |
柳毓松, 廉培庆, 同登科, 等. 利用遗传算法进行水平井水平段长度优化设计[J]. 石油学报, 2000, 21(4): 80-86. LIU Yusong, LIAN Peiqing, TONG Dengke, et al. Optimum design of the horizontal section length in a horizontal well using genetic algorithm[J]. Acta Petrolei Sinica, 2000, 21(4): 80-86. doi: 10.3321/j.issn:0253-2697.2008.-02.027 |
| [18] |
聂延波, 李晓平, 宋代诗雨. 水平井段优化设计方法综述[J]. 西部探矿工程, 2011, 23(5): 82-84. NIE Yanbo, LI Xiaoping, SONGDAI Siyu. Horizontal section optimization design methods[J]. West-China Exploration Engineering, 2011, 23(5): 82-84. doi: 10.3969/j.issn.1004-5716.2011.05.028 |
| [19] |
NOVY B J. Pressure drops in horizontal wells:When can they be ignored[C]. SPE 24941-PA, 1992. doi:10.2118/-24941-PA
|
| [20] |
陈海龙, 李晓平, 李其正. 水平井段最优长度的确定方法研究[J]. 西南石油学院学报, 2003, 25(1): 47-48, 61. CHEN Hailong, LI Xiaoping, LI Qizheng. Study of the determining method of optimum length on horizontal well[J]. Journal of Southwest Petroleum Institute, 2003, 25(1): 47-48, 61. doi: 10.3863/j.issn.1674-5086.2003.01.013 |
| [21] |
王大为, 李晓平. 水平井水平段长度优化原则[J]. 新疆石油地质, 2011, 32(2): 164-166. WANG Dawei, LI Xiaoping. Optimization principles for horizontal wellbore length[J]. Xingjiang Petroleum Geology, 2011, 32(2): 164-166. |
| [22] |
陈要辉, 闫铁, 刘颖, 等. 水平井水平段合理长度经济评价研究[J]. 天然气工业, 2006, 26(8): 151-153. CHEN Yaohui, YAN Tie, LIU Yin, et al. Research on the reasonable horizontal interval length of horizontal wells[J]. Natural Gas Industry, 2006, 26(8): 151-153. doi: 10.3321/j.issn:1000-0976.2006.08.047 |
| [23] |
梁冠民, 周生田. 水平井筒摩擦压降对井产能的影响[J]. 断块油气田, 2007, 14(5): 53-55, 66. LIANG Guanmin, ZHOU Shengtian. Influence of friction pressure drop along horizontal wellbore on well productivity[J]. Fault-Block Oil & Gas Field, 2007, 14(5): 53-55, 66. doi: 10.3969/j.issn.1005-8907.2007.05.019 |
| [24] |
KUCHUK F J, GOODE P A, WILKINSON D J, et al. Pressure transient behavior of horizontal wells with and without gas cap or aquifer[C]. SPE 17413-PA, 1988. doi:10.2118/17413-PA
|
| [25] |
李晓平, 张烈辉, 李允, 等. 水平井井筒内压力产量变化规律研究[J]. 水动力学研究与进展, 2005, 20(4): 492-496. LI Xiaoping, ZHANG Liehui, LI Yun, et al. Variation laws of pressure and production rate in horizontal well[J]. Journal of Hydrodyn Amics, 2005, 20(4): 492-496. doi: 10.3969/j.issn.1000-4874.2005.04.013 |
| [26] |
代磊, 黄全华, 杨颖. 水平井水平段长度计算研究[J]. 重庆科技学院学报(自然科学版), 2010, 12(2): 68-70. DAI Lei, HUANG Quanhua, YANG Ying. Length calculation research on horizontal section of horizontal well[J]. Journal of Chongqing University of Science and Technology (Natural Science Edition), 2010, 12(2): 68-70. doi: 10.3969/j.issn.1673-1980.2010.02.021 |
| [27] |
付锁堂, 费世祥, 叶珍, 等. 致密砂岩气藏水平井参数优化[J]. 天然气工业, 2018, 38(4): 101-110. FU Suotang, FEI Shixiang, YE Zhen, et al. Optimization of key parameters for horizontal well development of tight sandstone gas reservoirs[J]. Natural Gas Industry, 2018, 38(4): 101-110. doi: 10.3787/j.issn.1000-0976.2018.04.-012 |
| [28] |
DIKKEN B J. Pressure drop in horizontal wells and its effects on their production performance[C]. SPE 19824-PA, 1990. doi:10.2118/19824-PA
|
 2019, Vol. 41
2019, Vol. 41


