2. 西南石油大学博士后科研流动站, 四川 成都 610500;
3. 中国石化西南油气分公司勘探开发研究院, 四川 成都 610041;
4. 西南石油大学国家大学科技园, 四川 成都 610500;
5. “油气藏地质及开发工程”国家重点实验室·西南石油大学, 四川 成都 610500
2. Postdoctoral Research Station, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. Exploration and Production Research Institute, Southwest Oil & Gas Company, SINOPEC, Chengdu, Sichuan 610041, China;
4. National Science Park, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
5. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
水力压裂技术是页岩气藏效益开发的关键技术手段,在压裂过程中,裂缝的起裂扩展规律及导流特性是决定储层的改造体积及有效压裂周期的两大关键因素[1-5]。受地应力、岩石强度以及天然裂缝发育程度等因素的影响,压裂会形成包括充填裂缝、剪切滑移缝和原位闭合缝在内的多种复杂裂缝[6-7]。随着缝网复杂程度的增大,人工裂缝中支撑剂的平均支撑浓度小于0.5 kg/m
自支撑裂缝导流能力受裂缝滑移程度、表面粗糙度、岩石力学性质以及闭合应力等多种因素的共同影响。目前,对于裂缝导流能力的数学模型主要利用欧式几何参数建立,包括单一裂缝面几何参数和对应面叠合参数。前者的表征参数应用最广泛的是表面粗糙度[12-14],采用10条标准轮廓线来表征节理表面轮廓线的粗糙度,并得到国际岩石力学协会推荐使用,但是由于样本量过少,无法客观地进行定量对比,因而在使用中的误差较大[15]。近年来,有学者提出采用曲折比[16]、偏度和峰度[17]等参数来表征裂缝表面的粗糙程度;此外,也有学者提出了采用吻合度[18]、接触比[19]和裂缝开度标准方差[20]等裂缝面叠合参数来描述裂缝开度,进而建立裂缝导流能力数学模型。然而,这些统计学参数所包含的信息量有限,难以全面体现粗糙表面的随机行为和细节特征[21],且受测量仪器误差的影响相对较大,而分形理论具有解决复杂非线性问题的优势,分形维数可以克服测量仪器分辨率和取样长度等因素的影响,较为全面地反映裂缝面的形态特征[22-25]。本文采用分形理论来表征裂缝面叠合后流动空间的分布特征,建立考虑闭合应力作用下的裂缝导流能力预测模型。
1.1 物理模型自支撑裂缝由裂缝表面微凸体相互接触形成流动空间,将流体在裂缝内的流动进行简化处理(图 1),假设流体只沿裂缝长度方向流动,且为达西流;裂缝在闭合应力作用下只发生弹性变形;将各个流线等效为大量毛细管束,并引入表征毛管直径大小分布的分形维数
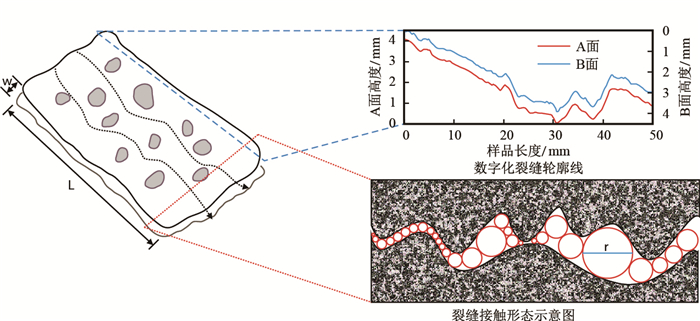 |
| 图1 物理模型示意图 Fig. 1 Schematic diagram of physical model |
多孔介质中的渗流遵循分形标度定律[26],则直径大于
| $ N(R > r) = {({r_{\max }}/r)^{{D_{\rm{f}}}}} $ | (1) |
式中:
毛细管实际长度
| $ {L_{\rm{e}}} = {r^{1 - {D_{\rm{t}}}}}{L^{{D_{\rm{t}}}}} $ | (2) |
令
由此,可将式(1)改写为
| $ N(R > r) = {({\lambda _{\max }}/r)^{{D_{\rm{f}}}{'}}} $ | (3) |
式中:
由于1 <
假设裂缝空间由
| $ - {\rm{d}}N(r) = {D_{\rm{f}}}{'}{\lambda _{\max }}^{{D_{\rm{f}}}{'}}{r^{ - ({D_{\rm{f}}}{'} + 1)}}{\rm{d}}r $ | (4) |
因此,裂缝流动空间可以通过毛细管的数量和截面积来表示
| $ V = \int_{{r_{\min }}}^{{r_{\max }}} {\dfrac{{{\rm{\pi }} {r^2}}}{4}{L_{\rm{e}}}} {\rm{d}}N\left( r \right) $ | (5) |
在闭合应力作用下,裂缝表面微凸体相互接触的变形机理复杂,会同时发生弹性变形和塑性变形甚至破碎,为简化数学模型,假设微凸体仅发生弹性变形。因此,毛细管直径
| $ r = \left( {1 - \sigma /E} \right){r_0} $ | (6) |
| $ {L_{\rm{e}}} = \left( {1 + \sigma \upsilon /E} \right)L $ | (7) |
式中:
将式(4)、式(6)和式(7)代入式(5),即可获得随闭合应力变化的裂缝空间体积
| $ V = \dfrac{{{\rm{\pi }} {L^{{D_{\rm{t}}}}}{D_{\rm{f}}}{'}\lambda _{\max 0}^{3 - {D_{\rm{t}}}}{{\left( {1 - \sigma /E} \right)}^{3 - {D_{\rm{t}}}}}}}{{4\left( {3 - {D_{\rm{f}}}{'} - {D_{\rm{t}}}} \right)}}\left[ {1 - {{\left( {\dfrac{{{r_{\min 0}}}}{{{\lambda _{\max 0}}}}} \right)}^{3 - {D_{\rm{f}}}{'} - {D_{\rm{t}}}}}} \right] $ | (8) |
式中:
在初始条件下,即不考虑闭合应力时的初始裂缝空间体积为
| $ {V_0} = \dfrac{{{\rm{\pi }} {L^{{D_{\rm{t}}}}}{D_{\rm{f}}}{'}\lambda _{\max 0}^{3 - {D_{\rm{t}}}}}}{{4\left( {3 - {D_{\rm{f}}}{'} - {D_{\rm{t}}}} \right)}}\left[ {1 - {{\left( {\dfrac{{{r_{\min 0}}}}{{{\lambda _{\max 0}}}}} \right)}^{3 - {D_{\rm{f}}}{'} - {D_{\rm{t}}}}}} \right] $ | (9) |
流体在单个毛细管中的流动符合Navier-Stokes方程[26]
| $ q = \dfrac{{{\rm{\pi }} {r^4}}}{{128\mu }}\dfrac{{{\rm{d}}p}}{{{\rm{d}}{L_{\rm{e}}}}} $ | (10) |
式中:
整个裂缝的流量即为
| $ Q = \int_{{r_{\min }}}^{{r_{\max }}} q {\rm{d}}N\left( r \right) $ | (11) |
将式(4)和式(10)代入式(11),即可得到随闭合应力变化的裂缝流量
| $ Q = \dfrac{{{\rm{\pi }} \Delta p{D_{\rm{f}}}{'}\lambda _{\max 0}^{3 + {D_{\rm{t}}}}{{(1 - \sigma /E)}^{3 + {D_{\rm{t}}}}}}}{{128\mu {L^{{D_{\rm{t}}}}}\left( {3 + {D_{\rm{t}}} - {D_{\rm{f}}}{'}} \right)\left( {1 + \sigma \upsilon/E} \right)}}\left[ {1 - {{\left( {\dfrac{{{r_{\min 0}}}}{{{\lambda _{\max 0}}}}} \right)}^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}{'}}}} \right] $ | (12) |
在初始条件下,即不考虑闭合应力时的流量为
| $ {Q_0}\!=\!\dfrac{{{\rm{\pi }} \Delta p{D_{\rm{f}}}{'}\lambda _{\max 0}^{3 + {D_{\rm{t}}}}}}{{128\mu {L^{{D_{\rm{t}}}}}\left( {3\!+\!{D_{\rm{t}}} - {D_{\rm{f}}}{'}} \right)}}\left[ {1\!-\!{{\left( {\dfrac{{{r_{\min 0}}}}{{{\lambda _{\max 0}}}}} \right)}^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}{'}}}} \right] $ | (13) |
式中:
通过数字化手段将两个对应裂缝面进行叠加即可获得初始裂缝流动空间
裂缝导流能力为裂缝渗透率和裂缝开度的乘积,其中,裂缝渗透率
| $ {K_{\rm{f}}} = \dfrac{{Q\mu L}}{{A\Delta p}} $ | (14) |
式中:
另外,裂缝开度
| $ w = \dfrac{A}{{N(r)}} $ | (15) |
因此,自支撑裂缝导流能力为
| $ {C_{\rm{f}}} = K_{\rm{f}}w = \dfrac{{Q\mu L}}{{\Delta pN(r)}} $ | (16) |
式中:
将式(3)和式(12)代入式(16),得到了利用裂缝开度分形维数和迂曲度分形维数进行表征,同时考虑闭合应力作用的自支撑裂缝导流能力数学模型
| $ {C_{\rm{f}}}\!\!=\!\!\dfrac{{{\rm{\pi }} \!{D_{\rm{f}}}{'}r_{\min 0}^{3\!+\! {D_{\rm{t}}}}{{(1\!-\!\sigma /E)}^{3\!+\!{D_{\rm{t}}}}}{L^{1\!-\! {D_{\rm{t}}}}}}}{{128\left(\!{3\!+\!{D_{\rm{t}}}\!-\!{D_{\rm{f}}}{'}} \!\right)\left(\!{1\!+\!\sigma v/E}\!\right)}}\left[ {{{\left(\!{\dfrac{{\lambda _{\max\!0}^{}}}{{{r_{\min\!0}}}}}\!\right)}^{3\!+\!{D_{\rm{t}}}\!-\! {D_{\rm{f}}}{'}}}\!-\!1} \right] $ | (17) |
上述数学模型从流动机理出发,引入两个分形维数(裂缝开度分形维数和迂曲度分形维数)来表征裂缝空间,同时基于弹性力学理论,考虑了裂缝空间在闭合应力作用下的变化过程,从而可以获得不同闭合应力下裂缝导流能力,为验证理论模型预测结果的准确性,开展了不同闭合应力下的裂缝导流能力实验。
2 实验测试 2.1 样品准备实验所用岩样取自威远地区龙马溪组一段3号小层,杨氏模量为23.5 GPa,泊松比为0.15,密度2.57 g/cm
 |
| 图2 裂缝导流能力实验岩样 Fig. 2 Experimental sample for fracture conductivity |
参照Freed[28]等人的自支撑裂缝导流能力测试实验,确定实验中的滑移量为2.5 mm,通过在相反的断面处贴铜箔垫片的方法来产生错位。
实验采用精密气驱实验装置(图 3),选择氮气为驱替介质,用造泡流量计测量气体流量。具体实验步骤为:(1)将打磨好的柱塞岩芯放入岩芯夹持器中,根据设定的滑移量放入金属垫片;(2)通入氮气,待流体通过稳定后,记录出口端压力,和对应时间段的流量;(3)改变围压至1 MPa,待流体通过稳定后,再次记录出口端压力和对应的流量;(4)继续依次改变围压(5
 |
| 图3 气测柱塞岩芯驱替装置实物图 Fig. 3 Gas gauge core plunger displacement device |
实验结果显示,裂缝滑移后的自支撑裂缝具备一定的导流能力,初期可达30
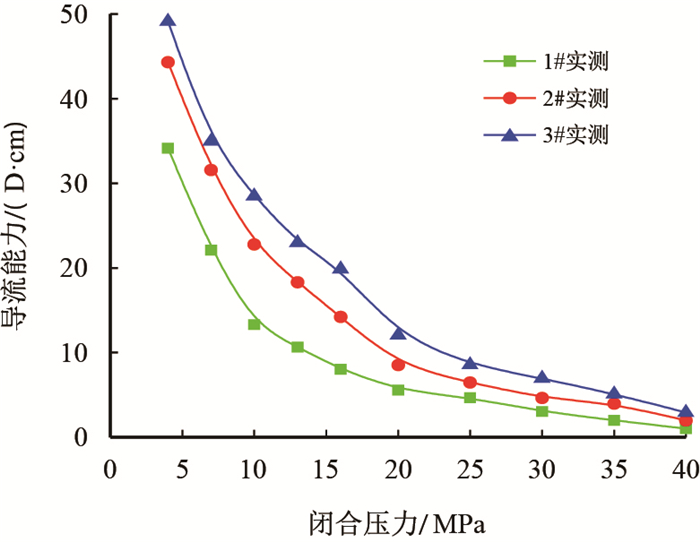 |
| 图4 裂缝导流能力与闭合压力关系曲线图 Fig. 4 Fracture conductivity versus closure stress |
利用本文建立的裂缝导流能力数学模型,对上述3个样品的裂缝导流能力进行理论预测,并将其与实验结果进行对比(图 5),结果显示,模型计算的预测曲线变化趋势与实测结果基本一致,且数值基本吻合。通过模型计算得到1#、2#和3#共3个样品的裂缝开度分形维
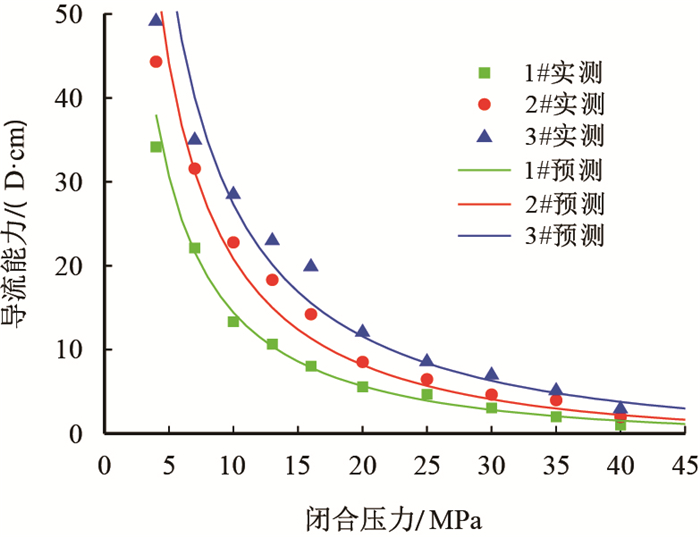 |
| 图5 模型计算结果和导流能力实验结果对比图 Fig. 5 Comparison between the model predictions and the experimental data |
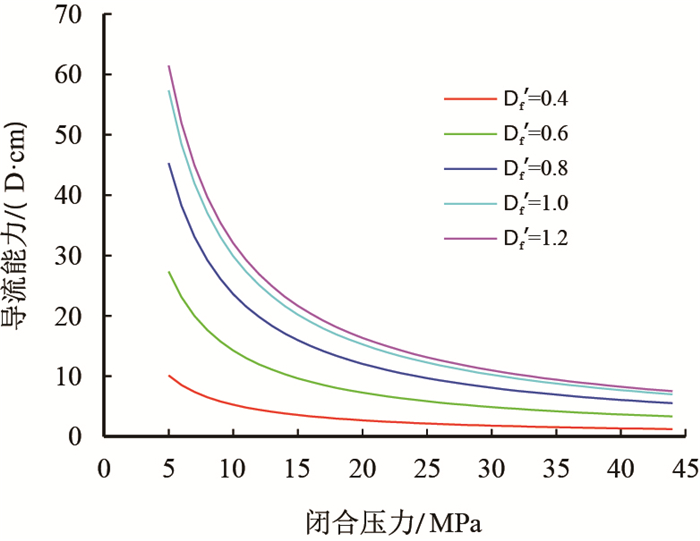
从前述物理模型中可知,
裂缝开度分形维数
 |
|
图6
不同 |
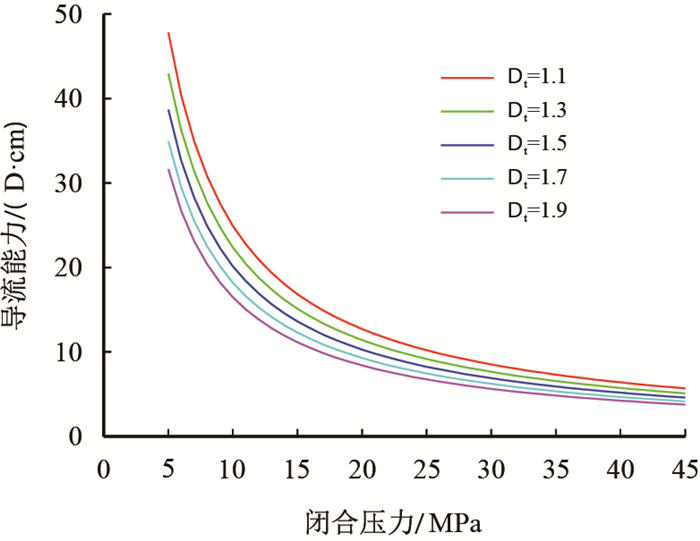
迂曲度分形维数
 |
|
图7
不同 |
根据上述敏感性分析结果可以对实验测试结果进行分析。1#样品的裂缝开度分形维数为0.8,表明其裂缝开度整体小于另外两块样品;迂曲度分形维数为1.8,即其裂缝空间迂曲程度均高于另外两块样品,表明流体的渗流阻力相对较大,两种因素共同作用导致其导流能力整体偏低。对于3#样品而言,其裂缝开度分形维数为0.95,迂曲度分形维数为1.5,表明其裂缝开度整体大于前两个样品,同时其裂缝空间的迂曲程度也最小,因而,在相同的闭合应力下,其裂缝导流能力均高于另外两个样品。
实验结果与模型预测结果的对比分析表明,将裂缝流动通道用具有分形特征的毛细管束来描述的方法是准确可行的,通过计算裂缝开度分形维数
(1) 利用迂曲度分形维数
(2)
(3) 基于分形理论建立的自支撑裂缝导流能力预测模型可大幅减少室内实验的工作量,同时预测结果具有尺度不变性,可有效表征水力压裂形成的自支撑裂缝渗流特征,为气井的产能评价及预测提供支撑。
| [1] |
蒋廷学, 周健, 张旭, 等. 深层页岩气井裂缝扩展及导流特性研究及展望[J]. 中国科学:物理学力学天文学, 2017, 47(11): 114603. JIANG Tingxue, ZHOU Jian, ZHANG Xu, et al. Overview and prospect of fracture propagation and conductivity characteristics in deep shale gas wells[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2017, 47(11): 114603. doi: 10.1360/SSPMA2016-00535 |
| [2] |
蒋廷学, 卞晓冰, 王海涛, 等. 深层页岩气水平井体积压裂技术[J]. 天然气工业, 2017, 37(1): 90-96. JIANG Tingxue, BIAN Xiaobing, WANG Haitao, et al. Volume fracturing of deep shale gas horizontal wells[J]. Natural Gas Industry, 2017, 37(1): 90-96. doi: 10.3787/j.issn.1000-0976.2017.01.011 |
| [3] |
李玉丹, 董平川, 周大伟, 等. 页岩气藏微裂缝表观渗透率动态模型研究[J]. 岩土力学, 2018, 39(增1): 42-50. LI Yudan, DONG Pingchuan, ZHOU Dawei, et al. A dynamic model of apparent permeability for micro fractures in shale gas reservoirs[J]. Rock and Soil Mechanics, 2018, 39(S1): 42-50. doi: 10.16285/j.rsm.2017.2218 |
| [4] |
李德旗, 何封, 欧维宇, 等. 页岩气水平井缝内砂塞分段工艺的增产机理[J]. 天然气工业, 2018, 38(1): 56-66. LI Deqi, HE Feng, OU Weiyu, et al. Mechanism of multistage sand filling stimulation in horizontal shale gas well development[J]. Natural Gas Industry, 2018, 38(1): 56-66. doi: 10.3787/j.issn.1000-0976.2018.01.007 |
| [5] |
车明光, 王永辉, 彭建新, 等. 深层超深层裂缝性致密砂岩气藏加砂压裂技术——以塔里木盆地大北、克深气藏为例[J]. 天然气工业, 2018, 38(8): 63-68. CHE Mingguang, WANG Yonghui, PENG Jianxin, et al. Sand fracturing technologies for deep and ultra-deep fractured tight sandstone gas reservoirs:A case study of Dabei and Keshen gas reservoirs in the Tarim Basin[J]. Natural Gas Industry, 2018, 38(8): 63-68. doi: 10.3787/j.issn.-1000-0976.2018.08.009 |
| [6] |
考佳玮, 金衍, 付卫能, 等. 深层页岩在高水平应力差作用下压裂裂缝形态实验研究[J]. 岩石力学与工程学报, 2018, 37(6): 1332-1339. KAO Jiawei, JIN Yan, FU Weineng, et al. Experimental research on the morphology of hydraulic fractures in deep shale under high difference of in-situ horizontal stresses[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1332-1339. doi: 10.13722/j.cnki.jrme.2018.0030 |
| [7] |
尹丛彬. 页岩压裂裂缝渗透率的测试与分析[J]. 天然气工业, 2018, 38(3): 60-68. YIN Congbin. Test and analysis on the permeability of fractured fractures in shale reservoirs[J]. Natural Gas Industry, 2018, 38(3): 60-68. doi: 10.3787/j.issn.1000-0976.2018.03.007 |
| [8] |
CIPOLLA C L, LOLON E P, ERDLE J C, et al. Reservoir modeling in shale-gas reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2010, 13(4): 638-653. doi: 10.2118/125530-MS |
| [9] |
王力.大庆外围低渗透储层自支撑压裂机理研究[D].大庆: 东北石油大学, 2016. WANG Li. The mechanism of self-supporting fracturing in Daqing's peripheral low permeability reservoir[D]. Daqing:Northeast Petroleum University, 2016. |
| [10] |
邹雨时, 张士诚, 马新仿. 页岩压裂剪切裂缝形成条件及其导流能力研究[J]. 科学技术与工程, 2013, 13(18): 5152-5157. ZOU Yushi, ZHANG Shicheng, MA Xinfang. Research on the formation conditions and conductivity of shear fracture for hydraulic fracturing in gas-shale[J]. Science Technology and Engineering, 2013, 13(18): 5152-5157. doi: 10.3969/j.issn.1671-1815.2013.18.013 |
| [11] |
ZHANG Junjing, KAMENOV A, ZHU D, et al. Laboratory measurement of hydraulic fracture condutivities in the Barnett shale[C]. SPE 163839-MS, 2013. doi:10.2118/163839-MS
|
| [12] |
RASOULI V, HOSSEINIAN A. Correlations developed for estimation of hydraulic parameters of rough fractures through the simulation of JRC flow channels[J]. Rock Mech Rock Eng, 2011, 44: 447-461. doi: 10.1007/s00603-011-0148-3 |
| [13] |
JAVADI M, SHARIFZADEH M, SHAHRIAR K, et al. Critical Reynolds number for nonlinear flow through rough-walled fractures:The role of shear processes[J]. Water Resources Research, 2014, 50(2): 1789-1804. doi: 10.1002/2013WR014610 |
| [14] |
LIU Richeng, LI Bo, JIANG Yujing, et al. Review:Mathematical expressions for estimating equivalent permeability of rock fracture networks[J]. Hydrogeology Journal, 2016, 24(7): 1623-1649. doi: 10.1007/s10040-016-1441-8 |
| [15] |
曹平, 贾洪强, 刘涛影, 等. 岩石节理表面三维形态特征的分形分析[J]. 岩石力学与工程学报, 2011, 30(增2): 3839-3843. CAO Ping, JIA Hongqiang, LIU Taoying, et al. Fractal analysis of Three-dimensional topography characteristics of rock joint surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3839-3843. |
| [16] |
庄园.基于数字化表征的酸蚀裂缝导流能力研究[D].成都: 西南石油大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10615-1014415606.htm
|
| [17] |
白翔.基于刻蚀形态数字化表征的酸蚀裂缝导流能力研究[D].成都: 西南石油大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015599364.htm
|
| [18] |
孙骏.利用分形方法研究裂缝面形态特征[D].成都: 成都理工大学, 2015. SUN Jun. Study of fracture surface morphology characteristics by using fractal method[D]. Chengdu:Chengdu Univerisity of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10616-1015311239.htm |
| [19] |
LI Bo, JIANG Yujing, KOYAMA T, et al. Experimental study of the hydro-mechanical behavior of rock joints using a parallel-plate model containing contact areas and artificial fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(3): 362-375. doi: 10.1016/j.ijrmms.2007.06.004 |
| [20] |
ISHIBASHI T, WATANABE N, HIRANO N, et al. Beyond laboratory scale prediction for channeling flows through subsurface rock fractures with heterogeneous aperture distributions revealed by laboratory evaluation[J]. Journal of Geophysical Research:Solid Earth, 2015, 120(1): 106-124. doi: 10.1002/2014JB011555 |
| [21] |
SAYLES R S, THOMAS T R. Surface topography as a nonstationary random process[J]. Nature, 1978, 271(5644): 431-434. doi: 10.1038/271431a0 |
| [22] |
张学良, 黄玉美, 傅卫平, 等. 粗糙表面法向接触刚度的分形模型[J]. 应用力学学报, 2000, 17(2): 31-35. ZHANG Xueliang, HUANG Yumei, FU Weiping, et al. Fractal model of normal contact stiffness between rough surfaces[J]. Chinese Journal of Applied Mechanics, 2000, 17(2): 31-35. doi: 10.3969/j.issn.1000-4939.2000.02.006 |
| [23] |
李菊花, 郑斌. 微观孔隙分形表征新方法及其在页岩储层中的应用[J]. 天然气工业, 2015, 35(5): 52-59. LI Juhua, ZHENG Bin. A new method for fractal characterization of microscopic pores and its application in shale reservoirs[J]. Natural Gas Industry, 2015, 35(5): 52-59. doi: 10.3787/j.issn.1000-0976.2015.05.008 |
| [24] |
易成, 王长军, 张亮, 等. 基于两体相互作用问题的粗糙表面形态描述指标系统的研究[J]. 岩石力学与工程学报, 2006, 25(12): 2481-2492. YI Cheng, WANG Changjun, ZHANG Liang, et al. Study on description index system of rough surface based on Bi-body interaction[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2481-2492. doi: 10.3321/j.issn:1000-6915.2006.12.014 |
| [25] |
王金安, 谢和平, 田晓燕, 等. 岩石断裂表面分形测量的尺度效应[J]. 岩石力学与工程学报, 2000, 19(1): 11-17. WANG Jinan, XIE Heping, TIAN Xiaoyan, et al. Scale effect on fractal measurement of rock fracture surfaces[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(1): 16-17. doi: 10.3321/j.issn:1000-6915.2000.-01.003 |
| [26] |
TAN Xiaohua, LI Xiaoping, LIU Jianyi, et al. Study of the effects of stress sensitivity on the permeability and porosity of fractal porous media[J]. Physics Letters A, 2015, 379(39): 2458-2465. doi: 10.1016/j.physleta.2015.06.025 |
| [27] |
RIGBY S P, WATTSMITH M J, FLETCHER R S. Simultaneous determination of the pore-length distribution and pore connectivity for porous catalyst supports using integrated nitrogen sorption and mercury porosimetry[J]. Journal of Catalysis, 2004, 227(1): 68-76. doi: 10.1016/j.jcat.-2004.06.025 |
| [28] |
FREDD C N, MCCONNELL S B, BONEY C L, et al. Experimental study of fracture conductivity for waterfracturing and conventional fracturing applications[J]. Society of Petroleum Engineers Journal, 2001, 6(3): 288-298. doi: 10.2118/74138-pa |
 2019, Vol. 41
2019, Vol. 41


