2. 贵州航天电器股份有限公司, 贵州 贵阳 550009;
3. 中国石化胜利油田东辛采油厂, 山东 东营 257000
2. Guizhou Aerospace Electronics Co. Ltd., Guiyang, Guizhou 550009, China;
3. Dongxin Oil Production Plant, Shengli Oilfiled, SINOPEC, Dongying, Shandong 257000, China
潜油电泵作为一种重要的旋转机械,因其排量大、效率高等特点被广泛应用。为了提高电泵使用寿命,避免劣质泵下井,潜油电泵的装配质量分析变得越来越重要。潜油电泵的状态信号可分为振动、温度、声学、电参数等,其中振动信号是衡量工作状态极其重要的指标[1-3]。潜油电泵正常工作时,产生具有很强周期性的振动信号;当潜油电泵装配质量较差时,扬程、泵效等常规指标可能表现正常,但振动信号将会在幅值或周期上出现异常,表现为振动信号幅值波动或周期不稳定[4-6]。因此,在潜油电泵下井前,要在实验井进行振动信号测量及稳定性分析,以便于工程人员及时发现潜油电泵装配质量异常并返厂检修。由于振动信号的时域分析方法中通常使用振动信号峰峰值、峭度、有效值作为评价指标时只能反映信号的部分特征[7-8],不能反映潜油电泵存在装配质量问题时的不稳定性。相关分析法在信号的平稳性判定中具有较大优势,文献[9]分析了利用自相关函数分析法进行故障诊断的优势;文献[10]通过提取自相关函数序列作为平稳性特征,利用时间序列收敛性制定新的平稳性判别标准并通过实例验证其正确性。
本文针对在潜油电泵实验井获得的泵壳表面的振动信号进行分析,利用滑动叠加平均法及自相关分析得到一个定量反映振动信号稳定性的系数,并将其定义为稳定指数。相对于振动信号的有效值、峰峰值等统计量指标,振动信号稳定指数能够综合反映潜油电泵的振动幅值变化和振动周期变化情况,更适合判断潜油电泵振动信号是否平稳,能够直观、定量地评价信号的稳定性。
1 潜油电泵振动信号获取方法以低功耗处理器和三维加速度传感器为核心器件设计了潜油电泵振动信号采集装置,并进行了防水、防油、抗撞击设计,用于采集潜油电泵在实验井下工作时泵壳表面的三维振动信号。振动采集装置安装于潜油电泵泵壳外表面,该装置在潜油电泵实验井内的工作位置示意图如图 1所示,其中实验井井深约为50 m。
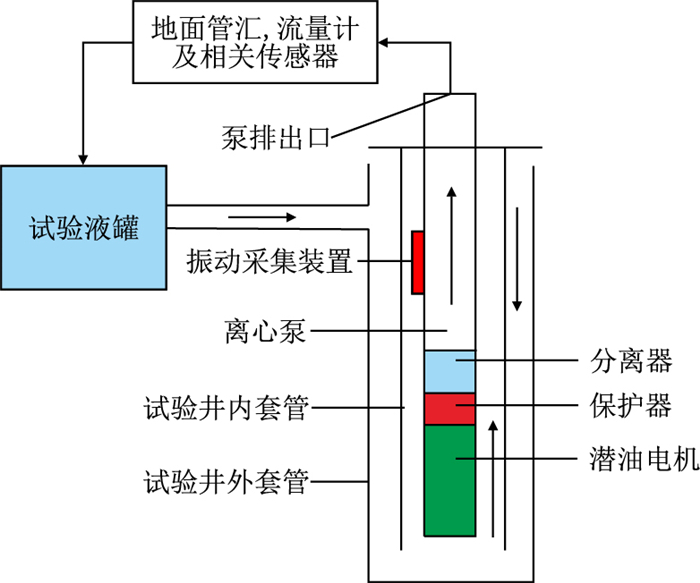 |
| 图1 实验井下振动采集装置位置示意图 Fig. 1 The location of the vibration collector device under the test well |
振动采集装置采集到的正常泵的3个维度(
| $ a = \sqrt {{a_x}^2 + {a_y}^2 + {a_z}^2} $ | (1) |
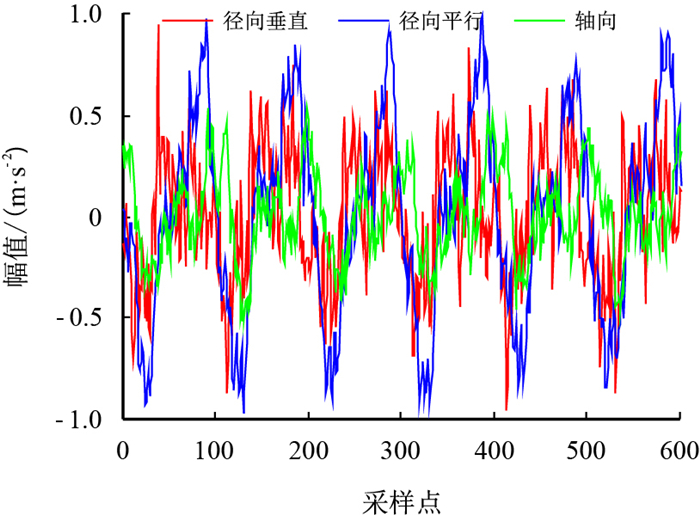 |
| 图2 潜油电泵振动信号波形图 Fig. 2 The waveform figure of vibration signal data of ESP |
式中:
在通过平移窗信号自相关分析法求取稳定指数,用于定量分析井下潜油电泵振动信号的稳定性时,窗信号和自相关系数的求取是稳定指数求解过程中的重要环节。本文利用滑动叠加平均法求取窗信号,再将该窗信号用于信号自相关分析中求取振动信号的自相关系数序列,从而利用潜油电泵振动信号的周期性求取稳定指数。以下对滑动叠加平均法与自相关分析的原理方法进行详细介绍。
2.1 滑动叠加平均法求取窗信号在现代信号处理中,为实现某一段信号的选取通常采用加矩形窗的方式进行,这是一种最直接且快速的方式。该方法通常是根据矩形窗的宽度决定所选择信号的长度,但是通过加矩形窗的方式选取出的窗信号具有任意性和随机性。例如,当信号中存在由较强干扰引起的突变信号时,利用简单的加矩形窗的方式选取的窗信号中若包含突变信号,则该窗信号便是一种特殊样例从而失去代表性。同时,潜油电泵的振动信号具有非平稳的周期性,为获取最能代表该组信号周期特性的窗信号,本文利用滑动叠加平均法求取窗信号。滑动叠加平均法作为一种常用周期信号处理方法,广泛应用于周期信号的检测与提取及信号信噪比的提高等领域[12]。其中滑动叠加平均法表达式为
| $ {x_{\rm{W}}}\left( j \right) = \dfrac{1}{M}\sum\limits_{n = 0}^{M - 1} x \left( {j + nN} \right){\rm{ }} 0 \leqslant n \leqslant M $ | (2) |
式中:
利用该方法求取窗信号的具体实现步骤为:(1)利用切尾平均法剔除整段信号异常值;(2)以
由滑动叠加平均法求取窗信号的实现步骤可知,该方法与直接加矩形窗或其他窗函数相比,能够避免选取的窗信号中包含特殊信号。本文对振动信号通过滑动叠加平均法处理得到的窗信号定义为该段信号以周期为单位的周期均值信号,该窗信号从统计上与该组信号整体数据特征最为接近。其中,信号分段、滑动叠加平均得到窗信号的示意图见图 3所示。
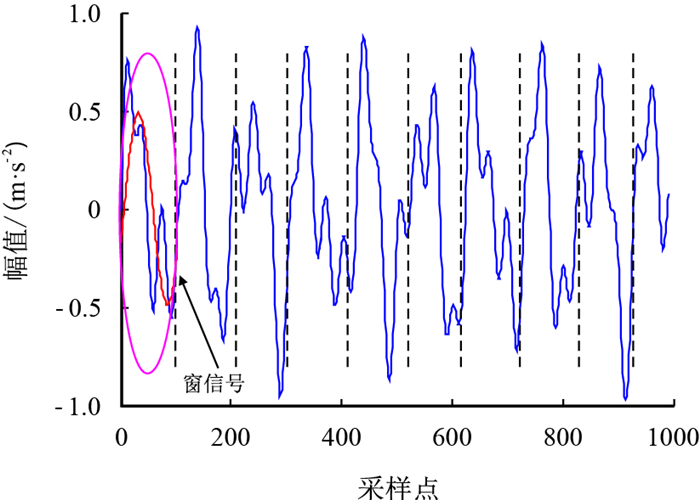 |
| 图3 滑动叠加平均法求取窗函数示意图 Fig. 3 Sliding overlay average method to obtain window function schematic |
在振动信号测量中,通常使用有效值来表示信号强度的大小[13]。对连续5 s的振动加速度信号求取有效值
| $ {X_{{\rm{rms}}}} = \sqrt {\dfrac{1}{{{N_1}}}\sum\limits_{i = 1}^{{N_1}} {x{{\left( i \right)}^2}} } $ | (3) |
式中:
| $ {\sigma _x}^2 = \dfrac{1}{{{N_1}}}\sum\limits_{i = 1}^{{N_1}} {{{\left[ {x(i) - \overline x } \right]}^2}} $ | (4) |
式中:
在振动信号时域分析法中,信号的自相关函数反映的是信号在一定延时
| $ {\rho _x}(\tau ) = \dfrac{{{R_x}(\tau )}}{{{\sigma _x}}} = \dfrac{{\dfrac{1}{N}\sum\limits_{i = 1}^N {\left[ {x(i) x(i + \tau )} \right]} }}{{\sqrt {\dfrac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {x(i) - \overline x } \right]}^2}} } }} $ | (5) |
令
| $ {\rho _x}(\tau ) = \dfrac{{{R_x}(\tau )}}{{{\sigma _x}}}{\rm{ = }}\dfrac{{{R_x}(\tau )}}{{{X_{{\rm{rms}}}}}} $ | (6) |
式中:
传统连续信号的自相关系数是某一时刻点信号
| $ \rho (i) = \dfrac{{\dfrac{1}{N}\sum\limits_{j = 1}^N {[{x_{\rm{W}}}(j) - \overline {{x_{\rm{W}}}} ][{x_i}(j) - \overline {{x_i}} ]} }}{{\sqrt {\sum\limits_{j = 1}^N {{{[{x_{\rm{W}}}(j) - \overline {{x_{\rm{W}}}} ]}^2} \cdot \sum\limits_{j = 1}^N {{{[{x_i}(j) - \overline {{x_i}} ]}^2}} } } }}{\rm{ }} $ | (7) |
式中:
由自相关系数的属性可知,对于周期信号及类周期信号,其自相关系数的大小也呈周期性变化[15-16]。利用以上方法求得的自相关系数序列中的峰值表示以周期信号为单位的信号相关程度最大点,即该段信号为整段信号中的某一周期信号。本文通过式(8)定义稳定指数
| $ S{\rm{ = }}\overline {{\rho _{{\rm{peak}}}}} {\rm{ = }}\dfrac{1}{M}\sum\limits_{t = 1}^M {{\rho _{{\rm{peak}}}}\left( t \right)} $ | (8) |
式中:
综上所述,窗信号表示振动信号以周期为单位的分段信号的均值大小,能够反映整体的振动信号的强度;通过式(7)得到的自相关系数序列能够反映振动信号以周期长度为单位的信号之间的相关程度;通过式(8)得到的稳定指数能够综合反映振动信号的周期稳定性和强度稳定性并且对于整段振动信号具有遍历性及代表性,信号周期稳定性与强度稳定性越强,稳定指数越大。其中,该方法的具体实现步骤为:
(1) 对采集的三维振动信号合成后进行降噪处理,得到降噪后的振动信号
潜油电机作为驱动潜油电泵开采石油的一种重要机械,其根本属性为一种竖立悬挂式的两极三相交流异步电机,其额定转速一般为2 850 r/min。潜油电泵在潜油电机的带动下实现原油的传输,其转速与电机转速基本保持一致。在实验井上进行多组电泵性能实验,统计转速数据发现,实验时电泵转速主要集中在2 850~2 930 r/min,对应电泵转动频率为47.5~48.8 Hz。由于电泵振动信号的基频与转速一致,所以,电泵的振动信号基频范围为47.5~48.8 Hz[17-18]。当振动信号基频为47.5 Hz、采样频率为5.0 kHz时,每个周期的采样点数
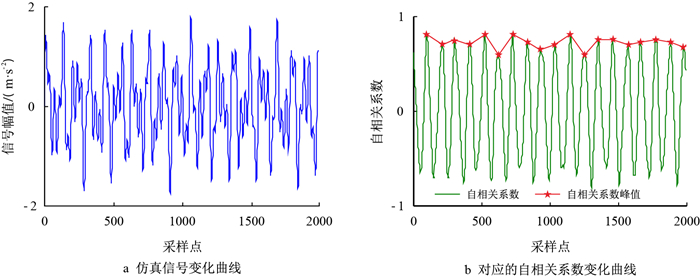 |
| 图4 正常信号振动幅值与自相关系数 Fig. 4 Normal signal vibration amplitude and autocorrelation coefficient |
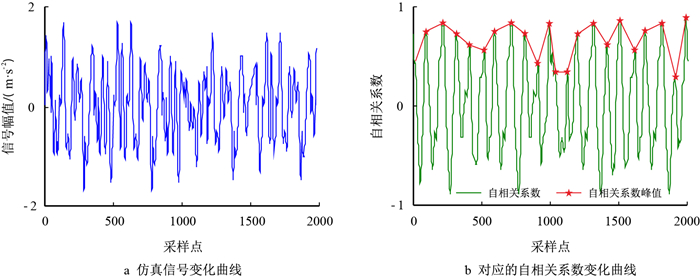 |
| 图5 周期随时间变化的信号幅值与自相关系数 Fig. 5 Signal amplitude and autocorrelation coefficient of periodic variation over time |
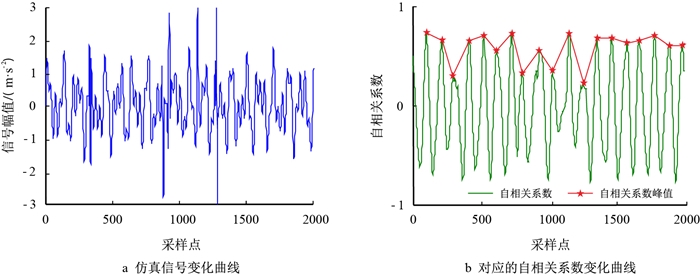 |
| 图6 存在随机冲击信号的振动幅值与自相关系数 Fig. 6 ibration amplitude and autocorrelation coefficient of random shock signal |
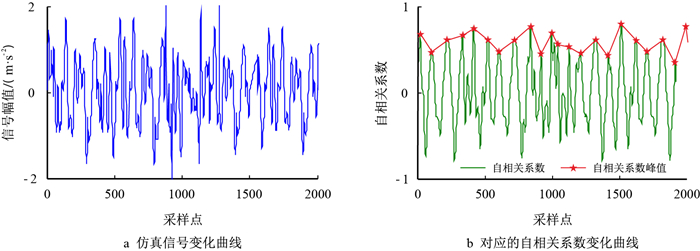 |
| 图7 周期、幅值均不稳定的振动幅值与自相关系数 Fig. 7 Vibration amplitude and autocorrelation coefficient with unstable period and amplitude |
对比图 4~图 7及表 1可以看出,对于周期及类周期信号,其自相关系数呈周期性变化,并且信号稳定性越差,稳定指数越小;对比图 4、图 5、图 7及表 1中数据可知,当出现信号周期随时间发生变化且变化无规律时,其有效值变化不明显且无规律,信号的稳定指数显著减小;对比图 4、图 6、图 7及表 1可知,当信号出现随机冲击信号时,其有效值变化较小,稳定指数显著减小;对比图 5、图 6、图 7及表 1可知,当综合信号周期与强度不稳定时见图 7,其稳定指数最小。因此,稳定指数既能反映信号强度大小也能反映信号周期的稳定性,能够定量评价信号的不稳定性程度,对于异常数据的指示效果明显。
| 表1 不同特征的仿真信号有效值与自相关系数对照表 Tab. 1 A comparison of the valid values and autocorrelation coefficients of simulated signals with different characteristics |
潜油电泵工作于井下井液中,工作环境恶劣,振动采集器采集到的振动数据存在噪声干扰[18]。因此,需要对合成加速度信号进行降噪处理,减小噪声对振动信号的影响。常用的降噪方法有时域平均法、中值滤波方法、小波阈值消噪法[19-20]等,由于振动信号的周期性与噪声信号的随机性,采用小波软阈值降噪法对原始振动信号进行降噪处理[21-23],提取有效信息。
图 8为某一次电泵测试数据中对合成振动信号进行降噪前后的波形图。
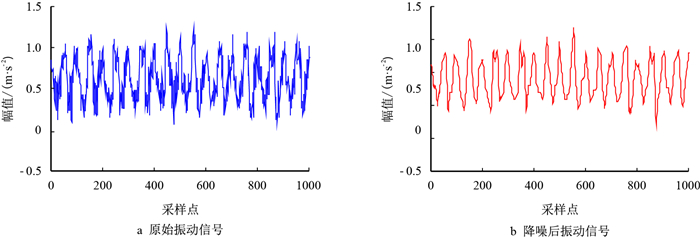 |
| 图8 振动信号降噪前后信号对比图 Fig. 8 Vibration signal before and after noise reduction signal comparison chart |
降噪后的振动信号除去了部分干扰信号且波形较原始信号更加平滑,能够为振动信号稳定性分析提供可靠的数据[24]。
4.2 实验结果分析以胜利油田某采油厂的潜油电泵实验井上所采集的50节泵的振动信号为例,对小波软阈值降噪后合成的振动数据,根据平移窗信号自相关分析方法得到了振动信号稳定指数,同时计算信号有效值,部分结果如表 2所示。
| 表2 实验数据分析结果表 Tab. 2 The results table of analyzing the experimental data |
国家标准化管理委员会发布的潜油电泵振动试验方法[13]中采用有效值作为振动信号检测标准,衡量振动信号振动强度的大小。表 2中1~50号泵中除35号泵的振动数据稳定指数值出现严重偏低的情况,其他均在正常范围内。第35号泵的原始合成数据波形见图 9所示,出现了振动加速度信号的周期及振动强度均不稳定的现象。
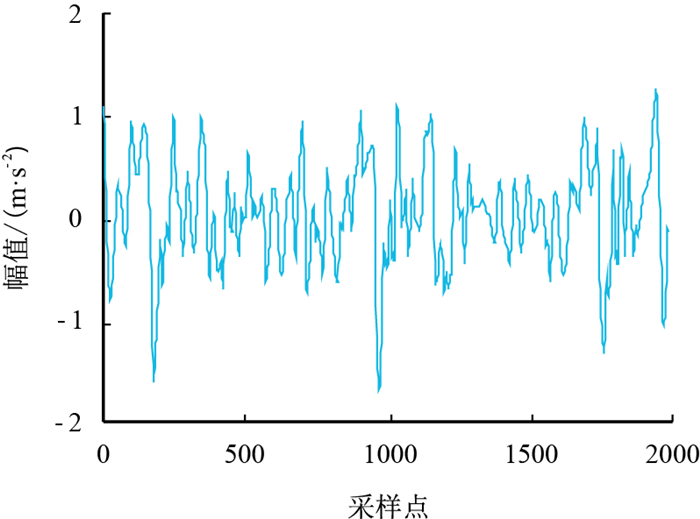 |
| 图9 35号泵的原始振动信号 Fig. 9 The original vibration signal of No. 35 pump |
因此,对第35号泵拆检,发现导轮与叶轮均为旧件,且导轮已出现轻微偏磨,其拆检图见图 10所示。分析该泵所在电泵机组的其他指标均未显示异常。若该泵下井很可能会在短时间内因偏磨故障而导致躺井,从而导致严重的经济损失。
 |
| 图10 35号泵拆检图 Fig. 10 No.35 pump demolition drawing |
(1) 设计了适用于潜油电泵实验井的井下振动信号采集系统,完成了振动信号的采集,并利用三维合成加速度表示井下振动信号的强弱并用于振动信号稳定性分析。
(2) 利用滑动叠加平均法求取能够代表周期特性的窗信号,避免了在自相关分析振动信号中选取窗信号的随机性。
(3) 通过窗信号的平移与等宽度振动信号的自相关分析得到具有与振动信号一致的周期性的自相关系数序列,并经过序列峰值的提取及计算得到稳定指数。对于稳定指数较低的电泵建议返厂拆检,及早发现潜在故障,避免机械故障给生产带来的经济损失、采油作业停滞等不良后果。
| [1] |
BARBINI L, OMPUSUNGGU A P, HILLIS A J, et al. Phase editing as a signal pre-processing step for automated bearing fault detection[J]. Mechanical Systems & Signal Processing, 2017, 91: 407-421. doi: 10.1016/j.ymssp.2016.12.004 |
| [2] |
FENG Zhipeng, MA Haoqun, ZUO Ming J. Vibration signal models for fault diagnosis of planet bearings[J]. Journal of Sound Vibration, 2016, 370: 372-393. doi: 10.1016/j.jsv.2016.01.041 |
| [3] |
司景萍, 高志鹰, 梁红波, 等. 基于瞬时基频的发动机表面振动信号时域定位[J]. 噪声与振动控制, 2010, 30(6): 153-156. SI Jingping, GAO Zhiying, LIANG Hongbo, et al. Time domain location of engine surface vibration signal based on instantaneous fundamental frequency[J]. Noise and Vibration Control, 2010, 30(6): 153-156. doi: 10.3969/j.issn.1006-1355.2010.06.037 |
| [4] |
王亚昆. 基于RSGWPT MSE和PNN的潜油电泵故障诊断方法[J]. 机械工程师, 2018(1): 167-170, 172. WANG Yakun. A diagnosis method for electrical submersible pump based on RSGWPT-MSE and PNN[J]. Mechanical Engineer, 2018(1): 167-170, 172. doi: 10.3969/j.issn.1002-2333.2018.01.057 |
| [5] |
马建仓, 刘小龙. 航空发动机转子振动信号的早期故障分析[J]. 计算机测量与控制, 2010, 18(2): 276-279. MA Jiancang, LIU Xiaolong. Early analysis of vibration signal for aero-engine rotor faults[J]. Computer Measurement & Control, 2010, 18(2): 276-279. |
| [6] |
余红英, 闫宏伟, 潘宏侠. 齿轮振动信号分解及其在故障诊断中的应用[J]. 振动、测试与诊断, 2005, 25(2): 109-113. YU Hongying, YAN Hongwei, PAN Hongxia. Gear vibration signal analysis and its application to fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(2): 109-113. doi: 10.3969/j.issn.1004-6801.2005.02.007 |
| [7] |
陈涛, 李林. 基于振动信号分析的齿轮故障诊断方法研究[J]. 科技广场, 2011(9): 29-33. CHEN Tao, LI Lin. Research of gear fault diagnosis' method based on analysis of vibration signal[J]. Science Mosaic, 2011(9): 29-33. doi: 10.3969/j.issn.1671-4792.2011.09.008 |
| [8] |
沈颖. 信号相关分析及其在工程测试中的应用[J]. 石油仪器, 2002, 16(6): 39-42. SHEN Ying. Signal correlation analysis and its application to engineering test[J]. Petroleum Instruments, 2002, 16(6): 39-42. doi: 10.3969/j.issn.1004-9134.2002.06.014 |
| [9] |
王建国, 吴林峰, 秦绪华. 基于自相关分析和LMD的滚动轴承振动信号故障特征提取[J]. 中国机械工程, 2014, 25(2): 186-191. WANG Jianguo, WU Linfeng, QIN Xuhua. Rolling bearing vibration signal fault feature extraction based on autocorrelation analysis and LMD[J]. China Mechanical Engineering, 2014, 25(2): 186-191. doi: 10.3969/j.issn.1004-132X.2014.02.009 |
| [10] |
管河山, 邹清明, 罗智超. 时间序列平稳性分类识别研究[J]. 统计与信息论坛, 2016, 31(4): 38. GUAN Heshan, ZOU Qingming, LUO Zhichao. Study on classification and identification of time series stationarity[J]. Statistics & Information Forum, 2016, 31(4): 3-8. doi: 10.3969/j.issn.1007-3116.2016.04.001 |
| [11] |
刘广孚, 朱赫, 周凯迪, 等. 基于改进K-means的潜油电泵质量评估方法研究[J]. 西南石油大学学报(自然科学版), 2018, 40(1): 173-180. LIU Guangfu, ZHU He, ZHOU Kaidi, et al. Study on the quality evaluation of electric submersible pumps based on improved K-means[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(1): 173-180. doi: 10.11885/j.issn.1674-5086.2016.11.25.02 |
| [12] |
李星蓉, 李永倩, 张硕. 同步叠加平均算法抑制噪声的Labview实现[J]. 华北电力大学学报, 2009, 36(4): 73-76. LI Xingrong, LI Yongqian, ZHANG Shuo. The LabView implement of synchronization overlapping average algorithm to suppress noise[J]. Journal of North China Electric Power University, 2009, 36(4): 73-76. doi: 10.3969/j.issn.1007-2691.2009.04.016 |
| [13] |
国家标准化管理委员会. GB/T 16750-2015潜油电泵机组国家标准[S].北京: 中国标准出版社, 2016: 61-62.
|
| [14] |
常兆光, 王清河, 杜彩凤. 应用统计方法[M]. 北京: 石油工业出版社, 2009. CHANG Zhaoguang, WANG Qinghe, DU Caifeng. Applied statistical methods[M]. Beijing: Petroleum Industry Press, 2009. |
| [15] |
吕苗荣, 丁宇, 徐清武. 基于自相关分析的离心泵振动信号的分段方法[J]. 自动化仪表, 2016, 37(10): 83-85. LÜ Miaorong, DING Yu, XU Qingwu. Segmentation method based on autocorrelation analysis for vibration signal of centrifugal pump[J]. Process Automation Instrumentation, 2016, 37(10): 83-85. |
| [16] |
HOLL M, KANTZ H. The relationship between the detrendend fluctuation analysis and the autocorrelation function of a signal[J]. European Physical Journal B, 2015, 88(12): 1-7. doi: 10.1140/epjb/e2015-60721-1 |
| [17] |
姚诚, 刘广孚, 谢文献, 等. 基于振动检测的潜油电泵机组转速测量方法的研究[J]. 仪表技术与传感器, 2008(12): 52-54. YAO Cheng, LIU Guangfu, XIE Wenxian, et al. Rotation speed measurement method for electrical submersible pumps based on vibration detecting[J]. Instrument Technique and Sensor, 2008(12): 52-54. doi: 10.3969/j.issn.1002-1841.2008.12.020 |
| [18] |
刘树林, 徐敏强, 董振刚, 等. 潜油电泵机组振动状态评估系统[J]. 大庆石油学院学报, 2008, 32(5): 58-60, 74. LIU Shulin, XU Minqinag, DONG Zhengang, et al. Vibration state assessment system for electric submersible pump unit[J]. Journal of Northeast Petroleum University, 2008, 32(5): 58-60, 74. doi: 10.3969/j.issn.2095-4107.2008.05.017 |
| [19] |
郑思莉, 桂预风, 陈先桥, 等. 小波阈值法在机械信号降噪研究中的应用[J]. 机械设计与制造, 2014(1): 222-225. ZHENG Sili, GUI Yufeng, CHEN Xianqiao, et al. The application of mechanical signals processing in wavelet threshold denoising method[J]. Machinery Design & Manufacture, 2014(1): 222-225. doi: 10.3969/j.issn.1001-3997.2014.01.068 |
| [20] |
王秉仁, 杨艳霞, 蔡伟, 等. 小波阈值降噪技术在振动信号处理中的应用[J]. 噪声与振动控制, 2008, 28(6): 9-12. WANG Binren, YANG Yanxia, CAI Wei, et al. Application of wavelet threshold de-noising technique in vibration signals processing[J]. Noise and Vibration Control, 2008, 28(6): 9-12. doi: 10.3969/j.issn.1006-1355.2008.06.003 |
| [21] |
陈涛, 徐小力, 王少红. 基于小波包惩罚函数的烟机振动信号软阈值降噪[J]. 北京理工大学学报, 2010, 30(8): 906-909, 914. CHEN Tao, XU Xiaoli, WANG Shaohong. Method of wavelet packet-based penalty function soft-threshold to de-noise vibration signals for flue gas turbine[J]. Transactions of Beijing Institute of Technology, 2010, 30(8): 906-909, 914. |
| [22] |
KABIR M A, SHAHNAZ C. Denoising of ECG signals based on noise reduction algorithms in EMD and wavelet domains[J]. Biomedical Signal Processing & Control, 2012, 7(5): 481-489. doi: 10.1016/j.bspc.2011.11.003 |
| [23] |
秦毅, 王家序, 毛永芳. 基于软阈值和小波模极大值重构的信号降噪[J]. 振动、测试与诊断, 2011, 31(5): 543-547. QIN Yi, WANG Jiaxu, MAO Yongfang. Signal denoising based on soft thresholding and reconstruction from dyadic wavelet transform modulus maximum[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 543-547. doi: 10.3969/j.issn.1004-6801.2011.05.001 |
| [24] |
THOMSONW T, MARIED D, 汤姆逊, 等. 振动理论及应用[M]. 北京: 清华大学出版社, 2005.
|
 2019, Vol. 41
2019, Vol. 41


