2. 中国石油大学(北京)机械与储运工程学院, 北京 昌平 102249
2. College of Mechanical and Transportation Engineering, China University of Petroleum, Changping, Beijing 102249, China
压裂混砂搅拌装置主要作用是配制不同压裂工艺要求的携砂液,携砂液质量的好坏与搅拌装置的混合特性有密切的联系。在压裂过程中,携砂液的密度是其重要的性能指标,而在实际压裂作业过程中压裂混砂车经常出现携砂液混合不均匀、质量不达标等问题,从而严重影响了压裂作业的效果[1-6]。为了使携砂液密度满足压裂工艺要求,混砂搅拌装置必须具有较强的搅拌作用和良好的搅拌效果,而搅拌作用的强弱及搅拌效果的好坏通常以搅拌装置混合液出口密度均匀程度及混合时间(混合液达到指定混合均匀程度所需时间)的长短进行度量[7-9]。
目前,针对压裂混砂搅拌装置混合时间的研究较少,但其他类型的搅拌装置混合时间的研究对混砂搅拌装置混合时间研究具有一定的借鉴作用。搅拌装置混合时间的研究主要采用实验测试和计算流体力学数值模拟两种方法。在搅拌装置混合时间实验测试时,获得搅拌装置混合时间的方法一般有电导率法、温差法以及光学法等[10-13]。采用实验方法测定搅拌装置混合时间时,受到实验方法、实验设备及实验条件各方面的限制,测定时不可能做到面面俱到,通常需要用几个监测点的结果来代替整个搅拌系统的结果,因此,所得结果的准确性将受到一定的影响[14-18]。近年来,随着计算流体力学(CFD)技术的快速发展,许多研究者采用数值模拟方法对搅拌装置混合时间进行了研究,并在各自的研究领域获得了相应的结论和规律。采用数值模拟方法预测混合时间可大大缩短实验周期、降低实验成本,而且可以得到整个混合罐内的信息,提高了结果的准确性,因此,CFD分析方法在搅拌装置混合时间预测方面的应用越来越广泛[19-24]。本文以某型号的压裂混砂车搅拌装置搅拌叶轮为研究对象,以搅拌装置混合时间为实验指标,采用正交实验法及CFD模拟相结合的方法研究搅拌叶轮的几何结构对混合时间的影响规律,为搅拌叶轮的结构优化提供理论支撑。
1 混砂搅拌装置几何结构本文以某型号的混砂搅拌装置为研究对象,该混砂搅拌装置包括具有射流作用的混合罐(图 1)和具有导流筒的双层搅拌叶轮(图 2)。
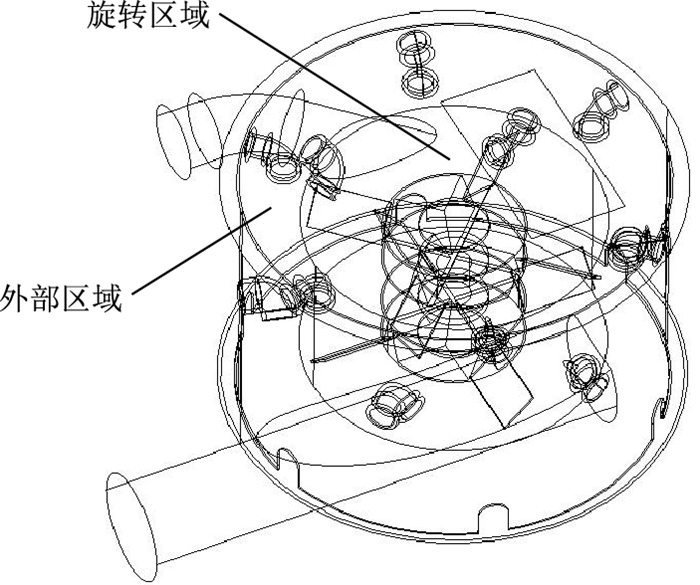 |
| 图1 混合罐结构示意图 Fig. 1 The structure of stirred tank |
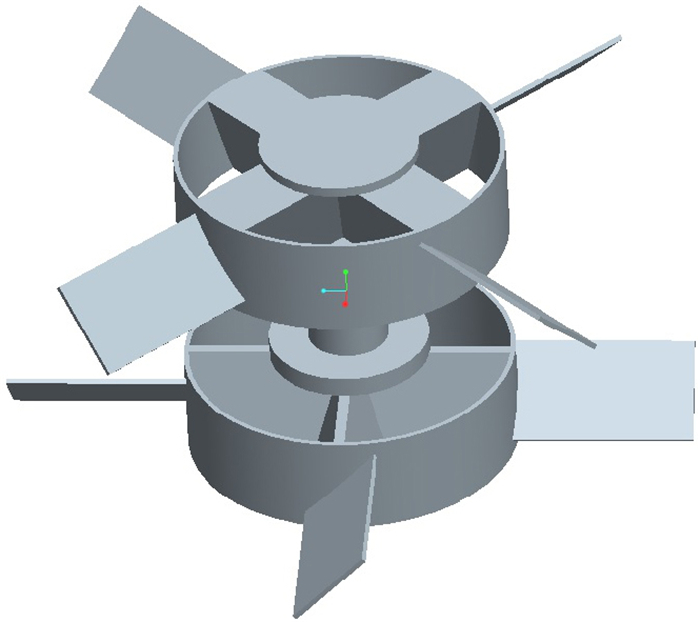 |
| 图2 搅拌叶轮结构示意图 Fig. 2 The structure of dual mixing impeller |
其中,混合罐包括内腔和夹层内腔两部分,混合罐内腔有上、中、下3层共18个进水口,其中,上层和中间层12个进水口为弯头进水口,下层进水口为6个孔。搅拌叶轮为具有导流筒的双层搅拌桨,由于混合罐的高度较大,为了加强搅拌混合作用,所以采用双层搅拌桨,分别由中间导流筒和4个桨叶组成。
2 混砂搅拌装置数值计算由于搅拌叶轮的转动导致混合罐内流体流动区域的形状不是固定的,而是随着叶轮的转动发生变化。为了解决数值模拟时混合罐内旋转的搅拌叶轮和静止的罐壁及进水弯头之间作用的问题,在对混砂搅拌装置进行数值模拟时拟采用搅拌叶轮非稳态处理方法中的滑移网格法。
在采用滑移网格方法对混砂搅拌装置进行数值模拟时,需要将混砂车混合罐计算区域分成两部分:中间部分为包括搅拌叶轮的旋转区域,外围部分为包括混合罐夹层及进水弯头的外部区域(图 1)。网格划分时,两部分相互独立,计算过程中旋转区域网格随搅拌叶轮进行转动,外部区域网格不发生变化。
为了保证旋转区域和外部区域的信息传递,需要在两部分的交界面上建立Mesh Interface,通过Mesh Interface采用插值实现旋转区域和外部区域质量和动量的守恒。在计算时,由于每经过一个时间步流体区域各参数需要进行更新,因此,滑移网格方法对计算机硬件要求较高,相同计算机硬件条件下,计算需要的时间较其他方法长,导致后处理过程较复杂,但是滑移网格方法在处理非稳态流场时可以得到较准确的计算结果。
根据混砂搅拌装置的结构特点,利用三维CAD软件Pro/E建立了其几何模型,并利用Pro/E布尔运算功能创建了搅拌装置的流体分析区域(包括叶轮旋转区域和外部区域)。
在所建立的混砂搅拌装置流体区域的基础上,将流体区域导入ANSYS Workbench中,采用ANSYS Workbench中Mesh模块对搅拌装置进行网格划分。为了提高计算精度,对混砂搅拌装置搅拌叶轮、混合罐夹层内腔入水口等重要区域进行网格划分时网格尺寸设置较小,而其他区域网格尺寸设置相对较大,混砂搅拌装置网格划分情况如图 3所示。
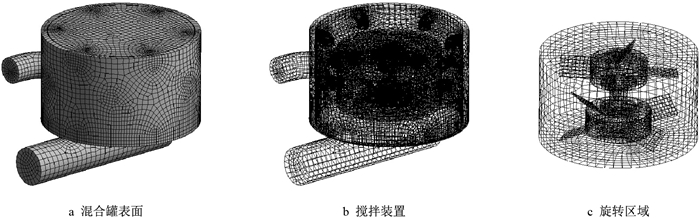 |
| 图3 搅拌装置网格划分结果 Fig. 3 The mesh of stirring device |
搅拌装置流体区域网格划分完成后,将其导入ANSYS软件流体分析模块Fluent软件中,然后根据混砂搅拌装置实际工作情况进行相应的参数设置。
3 实验方案为了研究搅拌叶轮直径及导流筒直径的大小对混砂搅拌装置混合时间的影响,本文主要考虑搅拌装置上叶轮直径(
在压裂混砂搅拌装置混合罐结构尺寸基础上,考虑搅拌叶轮的安装及干涉情况,上下叶轮直径可取最大值为864 mm,在此基础上对上下叶轮直径分别减小100 mm和200 mm,上下叶轮导流筒与叶轮直径比值在0.485的基础上加减0.080,因此,可得各影响因素水平取值情况如表 1所示。
| 表1 各因素水平情况 Tab. 1 The level of factors |
在忽略各因素之间交互作用的情况下,可选用正交表L
| 表2 搅拌装置混合时间正交实验方案及极差分析 Tab. 2 The orthogonal test scheme and range analysis of the mixing time for stirring device |
针对混砂搅拌装置压裂作业具体工况,本文在含砂比为30%、搅拌叶轮转速为100 r/min、搅拌装置排量为20 m
在正交实验方案CFD数值模拟的基础上,对混砂搅拌装置出口混合液密度进行了实时监测,各组实验中混砂搅拌装置出口混合液密度随时间的变化规律如图 4所示。
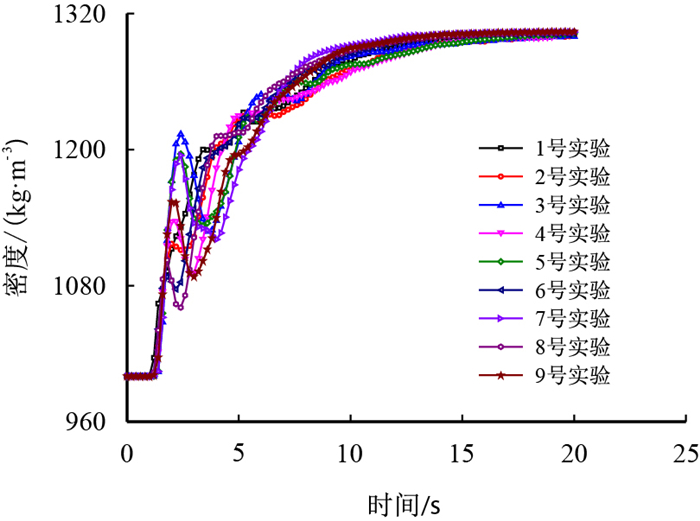 |
| 图4 搅拌装置出口混合液密度变化趋势 Fig. 4 The mixed liquid density of stirring device outlet |
根据压裂现场的具体情况,当混砂搅拌装置出口混合液密度在其理论密度(规定含砂比情况下)的±0.5%变化时,认为其均匀度可以满足压裂作业的要求。本文中数值模拟时含砂比为30%时,混砂搅拌装置出口混合液理论密度为1 301.6 kg/m
由混砂搅拌装置混合时间极差分析可以看出,各因素对搅拌装置混合时间影响程度的主次顺序为:
为了更为直观地看出各因素对搅拌装置混合时间的影响规律和趋势,以各因素水平值为横坐标,根据表 2中所得混合时间平均值为纵坐标,得到各因素与混合时间趋势如图 5所示。根据图 5可以看出,混合时间随着上下叶轮直径的增大呈减小的趋势;当上叶轮导流筒与叶轮直径比值取0.565时,混合时间平均值最小;当下叶轮导流筒与叶轮直径比值取0.485时,混合时间平均值最小。因此,可以得到最优方案为
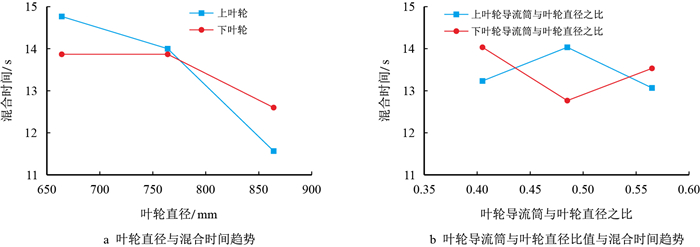 |
| 图5 各因素指标趋势图 Fig. 5 The factor index trend |
根据本节所得的最优方案
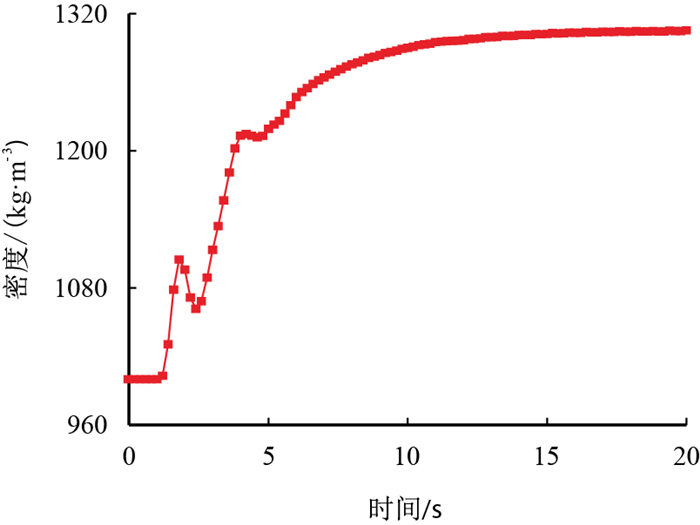 |
| 图6 最优方案搅拌装置出口混合液密度变化趋势 Fig. 6 The mixed liquid density of the optimal scheme for stirring device outlet |
(1) 通过混砂搅拌装置CFD正交实验数值模拟结果及极差分析可得搅拌叶轮的几何尺寸变化对混砂搅拌装置的混合时间有一定的影响,在含砂比为30%、搅拌叶轮转速为100 r/min的情况下,上叶轮直径对混合时间影响最大,为重要因素,其次为下叶轮直径和下叶轮导流筒与叶轮直径比值,而上叶轮导流筒与叶轮直径比值影响相对较小。
(2) 根据正交实验的极差分析及各影响因素对混合时间影响趋势的分析可得最优方案为
| [1] |
袁新梅, 周思柱, 黄天成, 等. 基于FLUENT的大排量混砂车搅拌罐结构优化[J]. 制造业自动化, 2014, 36(4): 150-152, 156. YUAN Xinmei, ZHOU Sizhu, HUANG Tiancheng, et al. Optimization structure of the mixing tank in the large displacement fracturing blender truck[J]. Manufacturing Automation, 2014, 36(4): 150-152, 156. doi: 10.3969/j.issn.1009-0134.2014.08.040 |
| [2] |
黄天成, 王德国, 周思柱, 等. 压裂混砂搅拌装置关键结构分析与流场模拟[J]. 石油机械, 2015, 43(11): 96-101. HUANG Tiancheng, WANG Deguo, ZHOU Sizhu, et al. Structural analysis and flow field simulation of fracturing sand mixing device[J]. China Petroleum Machinery, 2015, 43(11): 96-101. doi: 10.16082/j.cnki.issn.1001-4578.2015.11.020 |
| [3] |
黄天成, 周思柱, 陈翔, 等. HSC360型混砂车搅拌罐溅水现象分析及结构改进设计[J]. 长江大学学报(自科版), 2013, 10(1): 60-62. HUANG Tiancheng, ZHOU Sizhu, CHEN Xiang, et al. Splash phenomena analysis and structure improvement design for agitation tank of HSC360 blender truck[J]. Journal of Yangtze University (Natural Science Edition), 2013, 10(1): 60-62. doi: 10.3969/j.issn.1673-1409.2013.01.021 |
| [4] |
黄天成, 王德国, 周思柱, 等. 混砂车搅拌叶轮流固耦合模态分析研究[J]. 西南石油大学学报(自然科学版), 2012, 34(1): 165-170. HUANG Tiancheng, WANG Deguo, ZHOU Sizhu, et al. Modal research of fluid-solid coupling for the blender truck mixing impeller[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(1): 165-170. doi: 10.3863/j.issn.1674-5086.2012.01.026 |
| [5] |
HUANG Tiancheng, WANG Deguo, ZHOU Sizhu, et al. Numerical study of power characteristics for stirring device of sand blender[J]. Journal of Software Engineering, 2016, 10(2): 233-240. doi: 10.3923/jse.2016.233.240 |
| [6] |
HUANG Tiancheng, WANG Deguo, ZHOU Sizhu, et al. Theoretical design research for stirring device of fracturing blender truck[J]. Applied Mechanics & Materials, 2012, 220-223: 909-912. doi: 10.4028/www.scientific.net/amm.220-223.909 |
| [7] |
周思柱, 刘奔, 华剑, 等. 基于均匀设计的混砂车搅拌桨结构改进[J]. 机械设计与制造, 2013(5): 120-122. ZHOU Sizhu, LIU Ben, HUA Jian, et al. Structure improvement of the stirring paddle of fracturing blender truck based on uniform design[J]. Machinery Design & Manufacture, 2013(5): 120-122. doi: 10.3969/j.issn.1001-3997.2013.05.036 |
| [8] |
陈翔, 吴汉川, 乔春, 等. 基于正交实验法和流场模拟的搅拌罐结构优化设计[J]. 机械设计与制造, 2012(3): 55-57. CHEN Xiang, WU Hanchuan, QIAO Chun, et al. Optimum design for structure of agitation tank based on orthogonal test method and numerical simulation[J]. Machinery Design & Manufacture, 2012(3): 55-57. doi: 10.3969/j.issn.1001-3997.2012.03.021 |
| [9] |
HUANG Tiancheng, ZHOU Sizhu, YUAN Xinmei. Research on influencing factors for stirring effect of blender truck[J]. Advanced Materials Research, 2011, 308-310: 1454-1458. doi: 10.4028/www.scientific.net/AMR.308-310.1454 |
| [10] |
张庆华, 毛在砂, 杨超, 等. 搅拌反应器中液相混合时间研究进展[J]. 化工进展, 2008, 27(10): 1544-1550. ZHANG Qinghua, MAO Zaisha, YANG Chao, et al. Research progress of liquid-phase mixing time in stirred tanks[J]. Chemical Industry and Engineering Progress, 2008, 27(10): 1544-1550. doi: 10.3321/j.issn:1000-6613.2008.10.011 |
| [11] |
ZHAO Donglin, GAO Zhengming, HANS M S, et al. Liquid-phase mixing times in sparged and boiling agitated reactors with high gas loading[J]. Industrial & Engineering Chemistry Research, 2001, 40(6): 1482-1487. doi: 10.1021/ie000445w |
| [12] |
刘成勤, 胡玉泽. 电导滴定法测定聚酯浆料中对苯二甲酸含量[J]. 云南化工, 1999(2): 31-32, 62. LIU Chengqin, HU Yuze. Determination of p-phthalic acid in polyester paste by conductimetric titration[J]. Yunnan Chemical Technology, 1999(2): 31-32, 62. |
| [13] |
SHARP K V, ADRIAN R J. PIV study of small-scale flow structure around a rushton turbine[J]. AICHE Journal, 2001, 47(4): 766-778. doi: 10.1002/aic.690470403 |
| [14] |
HOLMES D B, VONCKEN R M, DEKKER J A. Fluid flow in turbine-stirred, baffled tanks-I, circulation time[J]. Chemical Engineering Science, 1964, 19(3): 201-208. doi: 10.1016/0009-2509(64)85030-2 |
| [15] |
吴越, 何建波, 刘谋用. 一种测量混合时间的新方法[J]. 实验力学, 1999, 14(1): 102-105. WU Yue, HE Jianbo, LIU Mouyong. A new mehtod for measuring the mixing time in stirring process[J]. Journal of Experimental Mechanics, 1999, 14(1): 102-105. |
| [16] |
徐世艾, 冯连芳, 顾雪萍, 等. 搅拌釜中自浮颗粒三相体系的混合时间[J]. 高校化学工程学报, 2000, 14(4): 328-333. XU Shiai, FENG Lianfang, GU Xueping, et al. Mixing time in stirred tank of three-phase gas-liquid-floating particle systems[J]. Journal of Chemical Engineering of Chineses Universities, 2000, 14(4): 328-333. doi: 10.3321/j.issn:1003-9015.2000.04.005 |
| [17] |
常新中, 腾文锐, 陈俊英. 9种搅拌器以水为介质混合时间的测定[J]. 河南科学, 2015, 33(4): 521-525. CHANG Xinzhong, TENG Wenrui, CHEN Junying. Mixing time measurement of nine agitators in water[J]. Henan Science, 2015, 33(4): 521-525. |
| [18] |
GABRIEL A. Mixing time in stirred vessels:A review of experimental techniques[J]. Chinese Journal of Chemical Engineering, 2015, 23(7): 1065-1076. doi: 10.1016/j.cjche.2014.10.022 |
| [19] |
PATWARDHAN A W, JOSHI J B. Relation between flow pattern and blending in stirred tanks[J]. Industrial & Engineering Chemistry Research, 1999, 38(8): 3131-3143. doi: 10.1021/ie980772s |
| [20] |
孟辉波, 王艳芬, 禹言芳, 等. 射流混合设备内混合时间的研究进展[J]. 化工进展, 2012, 31(12): 2615-2625. MENG Huibo, WANG Yanfen, YU Yanfang, et al. Research progress of mixing time in jet mixing equipment[J]. Chemical Industry and Engineering Progress, 2012, 31(12): 2615-2625. |
| [21] |
LUNDEN M, STENBERG O, ANDERSSON B. Evaluation of a method for measuring mixing time using numerical simulation and experimental data[J]. Chemical Engineering communications, 1995, 139(1): 115-136. doi: 10.1080/00986449508936401 |
| [22] |
SAHU A K, KUMAR P, PATWARDHAN A W, et al. CFD modelling and mixing in stirred tanks[J]. Chemical Engineering Science, 1999, 54(13): 2285-2293. doi: 10.1016/S0009-2509(98)00334-0 |
| [23] |
BUJALSKI J M, JAWORSKI Z, BUJALSKI W, et al. The influence of the addition position of a tracer on CFD simulated mixing times in a vessel agitated by a rushton turbine[J]. Chemical Engineering Research & Design, 2002, 80(8): 824-831. doi: 10.1205/026387602321143354 |
| [24] |
BUJALSKI W, JAWORSKI Z, NIENOW A W. CFD study of homogenization with dual rushton turbinescomparsion with experimental results. Part Ⅱ:The multiple reference frame[J]. Chemical Engineering Research and Design, 2002, 80(1): 97-104. doi: 10.1205/026387602753393402 |
 2019, Vol. 41
2019, Vol. 41


