引言

天然气偏差因子反映了真实天然气与理想气体的偏差程度，准确确定天然气偏差因子，是确定天然气其他各物性参数值^[1-3]、气藏地质储量、气井产能以及天然气集输工艺设计等的基础^[4-7]。天然气偏差因子可用实验测试^{[8, 9]}和理论计算两类方法确定，其中理论计算部分又包括基础理论^[10-14]与后面学者在此基础上的改进理论^[15-18]。对于常规的天然气，包括DAK方法在内的较多经验公式都可以获得精度较高的计算结果，但对于高含CO$_{{\rm 2}}$的酸性天然气而言，尽管CO$_{{\rm 2}}$的分子量与丙烷接近，临界温度与乙烷接近，临界压力却与乙烷、丙烷存在较大差异，导致了CO$_{{\rm 2}}$对天然气偏差因子的影响虽具有与乙烷、丙烷的相同趋势，但也表现出不完全一致的规律，从而影响常规方法的计算精度。国内外学者对高CO$_{{\rm 2}}$含量对天然气的偏差因子也做了相关研究^{[19, 20, 21]}，但多停留在计算方法的改进和不同计算方法的适应性分析层面上，少有实验测试数据验证。

应用DF气藏^[22]的流体样品，进行了CO$_{{\rm 2}}$含量对天然气偏差因子的影响规律实验，应用不同CO$_{{\rm 2}}$含量的天然气在气藏热力学条件下的偏差因子实验测试结果，研究了CO$_{{\rm 2}}$对天然气偏差因子影响规律，并修正了DAK天然气偏差因子计算经验公式。

1 天然气偏差因子实验测试 1.1 测试基本原理及方法

在任意温度压力下，$n$摩尔实际气体最简单的压缩型状态方程为

$ pV = Zn{\rm R}T $

(1)

式中：$p$—气体的压力，MPa；

$V$—气体体积，m$^{{\rm 3}}$；

$Z$—天然气偏差因子，无因次；

$n$—气体物质的量，kmol；

R—普适气体常数，R=8.314 kJ/(kmol$\cdot$K)；

$T$—温度，K(K = 273.15 + ℃)。

在标准状态下，实际气体接近于理想气体，则式(1)可写成

$ \left\{ \begin{array}{l} {p_0}{V_0} = {Z_0}n{\rm R}{T_0}\\ {Z_0} \approx 1 \end{array} \right. $

(2)

式中：$p_{0}$—标准状态压力，MPa；

$V_{0}$—气体在标准状态下的体积，m$^{{\rm 3}}$；

$Z_{0}$—气体标准状态下的偏差系数，无因次；

$T_{0}$—标准状态温度，K。

联合式(1)和式(2)，有

$ Z = \dfrac{{pV{T_0}}}{{{p_0}{V_0}T}} $

(3)

基于式(3)，可用PVT分析仪开展天然气的偏差因子实验测试。当实际气体与理想气体处于相同的压力和温度下时，偏差因子等于实际气体体积与理想气体体积之比，其大小描述了实际气体相对于理想气体压缩的难易程度，是分子体积特性和分子引力特性两个相反作用的综合结果。因此如何求得某种真实气体的偏差因子，是应用压缩状态方程的关键和难点。

本次实验测定仪器主要采用了法国ST公司PVT实验装置和气相色谱仪。实验测定时向PVT筒转入任意数量的待测真实气体，测定其在标准状态下的体积以及某地层温度下不同压力下的体积，即可通过式(3)计算该地层温度、不同压力下的偏差因子。

4种待测天然气均为依据DF气藏实际地层样品组成配制而成，具体如表 1所示，天然气中的CO$_{{\rm 2}}$含量分别为3.18%、10.35%、21.97%及50.09%。

1.2 测试结果及分析

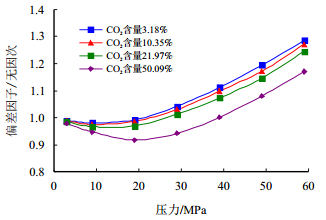
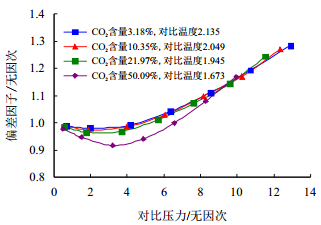
实验在模拟实际储层温度141 ℃下进行，压力从59 MPa降至3 MPa过程中记录不同压力下的体积，进而由式(3)可得到偏差因子，测试分析结果如图 1，图 2所示。

根据实验的结果，不同CO$_{{\rm 2}}$含量天然气偏差因子变化规律与常规天然气偏差因子变化规律相似，具有以下几个特点：(1)不同CO$_{{\rm 2}}$含量天然气偏差因子由下降趋势变成上升趋势时的压力约为20 MPa或对比压力约为3.2。(2) CO$_{{\rm 2}}$对偏差因子$Z$的影响具有与乙烷、丙烷相似的影响规律，随着CO$_{{\rm 2}}$含量增加，对比压力、对比温度均出现不同幅度降低，偏差因子出现明显的降低，且降低幅度越来越大。

2 考虑CO$_{{\rm 2}}$影响的偏差因子计算模型 2.1 DAK模型的适应性评价

以Starling和Carnahan修正的BWR状态方程为基础，Dranchuk和Abou-Kassem(DAK)应用1 500个原始的Standing-Kats偏差因子数据进行非线性回归分析，建立了11系数的偏差因子计算模型，如式(4)所示^[23]。

$ Z=1+\left({{A}_{1}}+\dfrac{{{A}_{2}}}{{{T}_{\rm pr}}}+\dfrac{{{A}_{3}}}{{{T}_{\rm pr}}^{3}}+\dfrac{{{A}_{4}}}{{{T}_{\rm pr}}^{4}}+\dfrac{{{A}_{5}}}{{{T}_{\rm pr}}^{5}}\right){{\rho }_{\rm r}}+\\{\kern 40pt} \left({{A}_{6}}+\dfrac{{{A}_{7}}}{{{T}_{\rm pr}}}+\dfrac{{{A}_{8}}}{{{T}_{\rm pr}}^{2}}\right){{\rho }_{\rm r}}^{2}-{{A}_{9}}\left(\dfrac{{{A}_{7}}}{{{T}_{\rm pr}}}+\dfrac{{{A}_{8}}}{{{T}_{\rm pr}}^{2}}\right){{\rho }_{\rm r}}^{5} +\\ {\kern 40pt} \dfrac{{{A}_{10}}}{{{T}_{\rm pr}}^{3}}{{\rho }_{\rm r}}^{2}\left(1+{{A}_{11}}{{\rho }_{\rm r}}^{2}\right){\rm e}^{-{{A}_{11}}{{\rho }_{\rm r}}^{2}} $

(4)

$ {{\rho }_{\rm r}}=0.27\dfrac{{{p}_{{\rm pr}}}}{Z{{T}_{{\rm pr}}}} $

(5)

式中：$T_{\rm pr}$—天然气拟对比温度，无因次；

$p_{\rm pr}$—天然气拟对比压力，无因次；

$\rho _{{\rm r}}$—天然气拟对比密度，无因次；

$A_{{\rm 1}}{\sim}A_{{\rm 11}}$—方程系数，其中，$A_{{\rm 1}}=0.326 50$，$A_{{\rm 2}}=-1.070 00$，$A_{{\rm 3}}=-0.533 90$，$A_{{\rm 4}}=0.015 69$，$A_{{\rm 5}}=-0.051 65$，$A_{{\rm 6}}=0.547 50$，$A_{{\rm 7}}=-0.736 10$，$A_{{\rm 8}}=0.184 40$，$A_{{\rm 9}}=0.105 60$，$A_{{\rm 10}}=0.613 40$，$A_{{\rm 11}}=0.721 00$。

DAK模型公式适用范围为$1.36 \leqslant T_{{\rm pr}} \leqslant 3.00$；$0.1 \leqslant p_{{\rm pr}} \leqslant 15.0$^[24]。

根据不同CO$_{{\rm 2}}$含量的天然气偏差因子实验测试，4个气样的$p_{{\rm pr}}$在0.506$\sim$12.897，$T_{{\rm pr}}$在1.673$\sim$2.135，满足DAK模型的使用条件。故应用DAK模型，使用解非线性问题的牛顿迭代法，可得到不同含量CO$_{{\rm 2}}$天然气偏差因子的值，将其与实验值进行对比，对比结果用平均相对误差来计量，定义偏差系数的平均相对误差为

$ {{E}_{\rm Z}}=\dfrac{1}{N} \sum\limits_{i=1}^{N}{\left| \dfrac{{{Z}_{\rm cal}}-{{Z}_{\exp }}}{{Z}_{\exp }} \right|}\times 100\% $

(6)

式中：$E_{{\rm Z}}$—平均相对误差，%；

$N$—实验数目；

$Z_{{\rm cal}}$—天然气偏差因子计算值，无因次；

$Z_{{\rm exp}}$—天然气偏差因子实验值，无因次。

最终，可得到不同CO$_{{\rm 2}}$含量天然气偏差因子实验值、模型计算值及平均相对误差，具体如表 2所示。

由表 2可见：(1)对不同CO$_{{\rm 2}}$含量的天然气而言，在压力高于17 MPa情况下，DAK模型计算的天然气偏差因子均高于实验值。(2)对任意一种CO$_{{\rm 2}}$含量的天然气而言，压力对DAK模型计算的偏差因子误差具有正相关性，误差随压力增大而增加。(3)当CO$_{{\rm 2}}$含量较低时，DAK模型计算的误差小于5.0%，能够对天然气偏差因子进行较精确的计算，但随着CO$_{{\rm 2}}$含量增大，平均相对误差($E_{\rm Z}$)越来越大，CO$_{{\rm 2}}$含量为50.09%的气样4最大平均误差已达7.9%。因此，当CO$_{{\rm 2}}$含量较高时，无法应用DAK模型准确计算天然气的偏差因子，需要对结果进行修正。

2.2 DAK模型修正

综合实验测试结果和DAK模型的产生过程可知，其不适用于高含CO$_{{\rm 2}}$天然气偏差系数的计算是由于其回归样本点中高CO$_{{\rm 2}}$的气样很少，为了得到适用于这样气体的压缩系数计算模型，可以借用DAK模型，采用高含CO$_{{\rm 2}}$天然气样本进行回归，修正其系数。基于文献[25]中CO$_{{\rm 2}}$含量为58%、66%及92%的气样数据(偏差因子$Z$测试结果)，利用麦夸特法及通用全局优化法对式(4)求解最优化问题，重新确定了DAK模型中的11个参数为：$A_{{\rm 1}}=3.638 9$，$A_{{\rm 2}}=-6.135 2$，$A_{{\rm 3}}=-18.872 0$，$A_{{\rm 4}}$=43.519 0，$A_{{\rm 5}}=-23.109 9$，$A_{{\rm 6}}=0.380 5$，$A_{{\rm 7}}=-1.346 7$，$A_{{\rm 8}}=1.778 9$，$A_{{\rm 9}}=0.197 3$，$A_{{\rm 10}}=-1.361 7$，$A_{{\rm 11}}=40.231 2$。

应用新修正参数的DAK模型可以得到气样5、气样6及气样7的天然气偏差因子$Z$值，如表 3所示。其平均相对误差均非常小，最大仅为2.2%，可以看出修正的模型能够非常准确地对高含CO$_{{\rm 2}}$天然气的偏差因子$Z$进行计算。

2.3 修正DAK模型检验

DF气藏CO$_{{\rm 2}}$含量为50.09%的气样4，DAK模型已不能对其偏差因子$Z$进行准确的计算，应用本文针对高含CO$_{{\rm 2}}$天然气偏差因子$Z$的DAK修正模型对其进行计算，同时，对CO$_{{\rm 2}}$含量为3.18%的气样1、CO$_{{\rm 2}}$含量为10.35%的气样2、CO$_{{\rm 2}}$含量为21.97%的气样3进行了计算，从而得到DAK修正模型的计算值(表 4)。

由表 4可以看到，针对气样4应用DAK修正模型计算的天然气偏差因子$Z$可以较好地与实验测试值拟合。此外，通过DAK修正模型与原DAK模型计算值的平均相对误差相比(表 2，表 4)可以发现：用DAK修正模型计算低CO$_{{\rm 2}}$含量的$Z$因子时，误差较大；但应用DAK修正模型计算CO$_{{\rm 2}}$含量50.09%的气样$Z$因子计算误差大幅度下降为1.2%，当压力高于11 MPa，平均计算误差均小于0.5%，说明本文的DAK修正模型对高CO$_{{\rm 2}}$含量的DF气藏的偏差因子能够更好地进行预测。

3 结论

(1) 不同CO$_{{\rm 2}}$含量天然气偏差因子由下降趋势变成上升趋势时的压力约为20 MPa。在同一温度及压力下，随着CO$_{{\rm 2}}$含量的增加，偏差因子出现明显的降低，且降低幅度越来越大。

(2) 当CO$_{{\rm 2}}$含量在50%以下时，偏差因子的经验公式(DAK方法)能够比较准确地计算出其参数值。

(3) 麦夸特法结合通用全局优化对DAK模型中的11个参数进行重新拟合，得到了DAK修正模型，应用新模型能够更加较准确地计算出天然气中CO$_{{\rm 2}}$含量大于50%时的偏差因子值，这对高CO$_{{\rm 2}}$含量气藏的开发具有重要的指导意义。