2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
研究认为,岩石物理性质与有效应力之间存在一定的函数关系[1-4]。在地面、原地条件和储层开采过程中,作为储层含油性评价重要参数的地层因素,有效应力变化会对其产生何种影响是一个值得探究的问题。1942年,Archie基于实验研究将饱和盐水的岩石电阻率(
| $ F = F (p_{\text{c}}, p_{\text{p}}) $ | (1) |
1925年,Terzaghi首次提出有效应力方程(peff=pc-pp)并用于疏松黏土矿物研究,但是,直接将
其后,围绕渗透率有效应力系数(
结合有效应力方程(
| $ F = F (p_{\text{c}}, p_{\text{p}}) = F (p_{\text{eff}}) = F (p_{\text{c}}$–$\alpha p_{\text{p}}) $ | (2) |
式中:
式(2)中的有效应力系数(
围绕地层因素有效应力,Brace等于1965年基于实验研究了应力变化对岩石电阻率的影响[18-19],实验过程中将内压近似为0,单一改变围压进行测试,结果显示,在一定压力范围内(约0~100 MPa),电阻率随围压的增加而急剧增加,表现出强烈的应力敏感性,而后(>100 MPa),其增幅趋于减缓。Thomas采用同样方式测试了围压变化对Berea砂岩和Muddy J砂岩电阻率的影响(饱和5.7
本文通过实验测试不同围压和内压作用下低渗透砂岩的地层因素,采用响应面函数对数据进行处理,获取不同围压和内压下的有效应力系数,得到了地层因素有效应力。同时,结合岩样微观结构建立微裂缝模型,分析了地层因素、有效应力及有效应力系数的变化规律。
1 实验研究 1.1 岩芯选取实验选取了7块来自鄂尔多斯盆地的砂岩样品,岩样长度均为6 cm,直径约为2.5 cm。岩样基本物性参数如表 1所示,其中,孔隙度主要在3.22%~13.31%,平均值为8.80%;渗透率主要在0.13~1.15 mD,平均值为0.34 mD,属于典型的低孔低渗砂岩。
| 表1 岩样基本物性参数 Tab. 1 The basic property data of the samples |
实验岩样均被切分为3段,最长的一段用于岩石地层因素的测试,另外两段分别用于扫描电镜和薄片研究。通过将岩样进行特殊的洗油、干燥处理后,在真空环境下采用100 000 mg/L的NaCl溶液进行饱和(饱和时间不少于7 d)。
矿物成分分析显示,岩样中石英含量为36.0%~40.0%,岩屑含量为35.6%~56.0%,填隙物含量为8.0%~10.0%,铸体薄片和扫描电镜(图 1)分析显示,岩样微裂缝发育。
 |
| 图1 岩样D4铸体薄片和扫描电镜分析图 Fig. 1 Casting thin section and SEM photos of sample D4 |
整个实验测试均在室温条件下(25 ℃)完成,实验前先测试得到NaCl溶液的电阻率,实验使用的设备包括:Teledyne Isco驱替泵、手动试压泵、电阻率岩芯夹持器、数字电桥、中间容器、回压装置和铂黑电极。
为了尽可能地模拟地层条件,设计围压30、35及40 MPa,最大内压35 MPa,并保证每个测量点的围压高于内压(
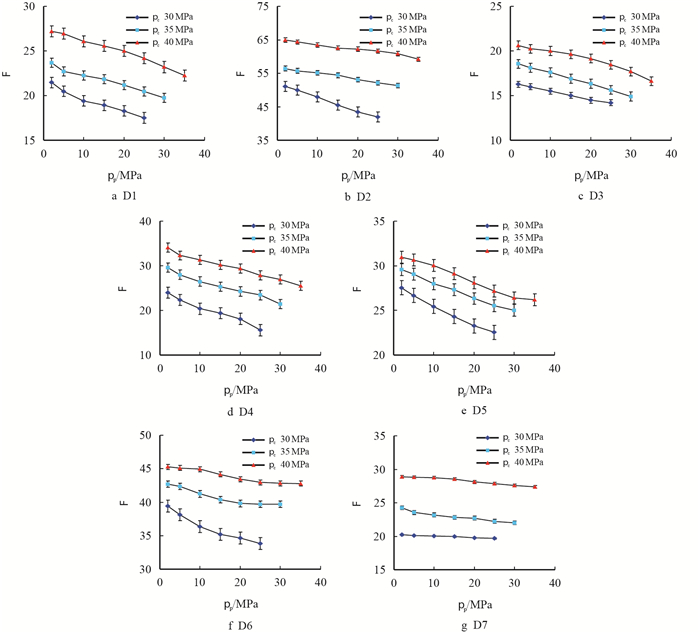 |
| 图2 岩样实验数据 Fig. 2 Experimental data for samples |
采用响应面函数对数据进行处理,响应面函数分析通过实验数据自身线性回归而不用假设任何先验参数,Warplnskl等[26]和Li等[12]将此方法成功用于渗透率有效应力的研究并验证了其优越性。地层因素同围压和内压的响应面函数关系可表示为
| $ F = a_{0} + a_{1}{p_{\text{c}}} + a_{2}{p_{\text{p}}} + a_{3}{p_{\text{c}}}{p_{\text{p}}} + a_{4}p_{\text{c}}^{2} + a_{5}p_{\text{p}}^{2} $ | (3) |
式中:系数
通过构建一个三维响应面
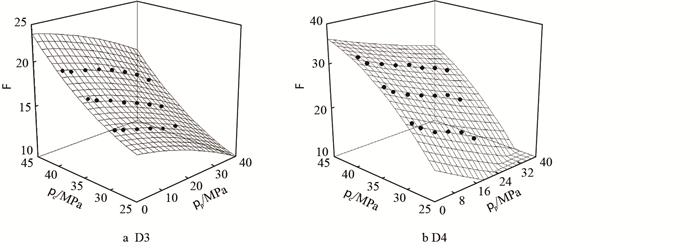 |
|
图3
岩样D3( |
| 表2 岩样响应面函数分析系数值 Tab. 2 The parameters of the response-surface function for samples |
有效应力系数的准确求取是运用有效应力分析的重要前提。
Terzaghi开始认为,有效应力系数(
Berryman基于理论推导分析认为,对于纯砂岩均质地层,当孔隙流体的电导可忽略时,有效应力系数为常数1[23-24];对于富含黏土的砂岩地层,有效应力系数
Bernabé认为,当方程
| $ \alpha = d{p_{\rm{c}}}/d{p_{\rm{p}}} = - (\partial F/\partial {p_{\rm{p}}})/\left( {\partial F/\partial {p_{\rm{c}}}} \right) $ |
联立式(3),可得
| $ \alpha_{\text{t}} =-\dfrac{a_{2} + a_{3}{p_{\text{c}}} + 2 a_{5}{p_{\text{p}}}}{a_{1} + a_{3}{p_{\text{p}}} + 2 a_{4}{p_{\text{c}}}} $ | (4) |
式(4)为采用切线方法计算得到的有效应力系数,称为切线有效应力系数
由式(4)可知,当
分析认为,切线法计算有效应力系数的方法并不能满足所有条件[12-13],采用切线法得到的有效应力系数在特定条件下会产生一定的误差。如图 4所示为基于响应面函数分析绘制地层因素等值线图,图中点
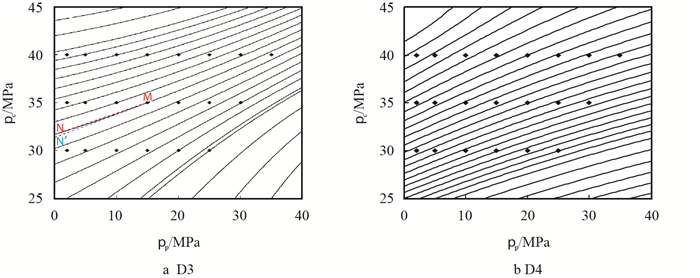 |
|
图4
样本D3,D4地层因素等值线图
Fig. 4
Iso- |
实际上,
| $ p_{\text{eff}, M} = p_{\text{c}, N} = p_{\text{c}, M}-\dfrac{p_{\text{c}, M}-p_{\text{c}, N}}{p_{\text{p}, M}} p_{\text{p}, M} $ |
此时对应的有效应力系数应表示为
| $ \alpha_{\text{s}} = \dfrac{p_{\text{c}, M}-p_{\text{c}, N}}{p_{\text{p}, M}} $ | (5) |
式(5)为采用割线方法得到的有效应力系数,称之为割线有效应力系数(
分别采用式(4)和式(5)计算实验获取的有效应力系数,分析发现,有效应力系数与有效应力(
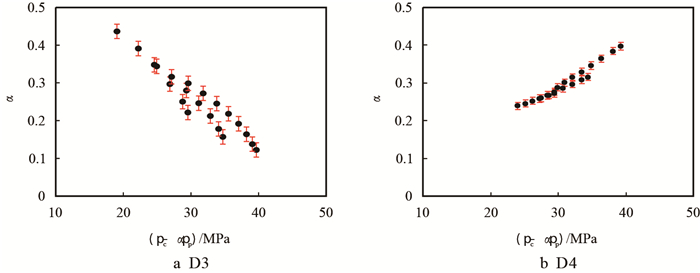 |
|
图5
样本D3、D4割线有效应力系数与 |
| 表3 样本有效应力系数取值范围 Tab. 3 Coefficient of the samples |
分析计算结果还可以发现,采用切线法得到的部分有效应力系数是明显不可取的(
为了有效剖析有效应力变化对地层因素的影响,实验过程中保证流体矿化度恒定,并忽略相关化学因素的影响。对于饱和盐水的砂岩岩芯,导电机理主要分为两类(忽略骨架的导电性):一类为孔隙空间内的流体电迁移导电;另一类为骨架颗粒表面导电[30]。Brace等研究认为[18],对于饱和高矿化度流体,孔隙空间内流体电解传导占居主导地位;而对于饱和低矿化度流体,骨架颗粒表面导电则起主导作用。本文主要讨论高矿化度流体饱和下微裂缝空间的电传导作用。
微裂缝的存在构成低渗砂岩有效导流路径[31-33],样本铸体薄片和扫描电镜(图 1)分析显示,本文研究的致密砂岩微裂缝明显发育,在围压和内压的作用下将会引起岩石表观体积的压缩或膨胀,而微裂缝的存在使得骨架和孔隙体积并不能保持整体均匀形变[23, 24]。因此,致密砂岩微裂缝随着内压和围压的张开和闭合必然会对地层因素产生明显影响。
数据处理结果显示,有效应力系数(
Terzaghi有效应力方程中有效应力系数为常数1,将其代入实验数据分析发现,地层因素和有效应力在二维坐标系中明显发散,并不能很好地拟合,表现为同一有效应力下对应地层因素为多个数值(如图 6空心圆点)。这与理论分析认为同一有效应力作用下岩石的地层因素也必然相同是明显相违悖的。这是因为有效应力系数为常数1时,有效应力即等于实际压力差,即
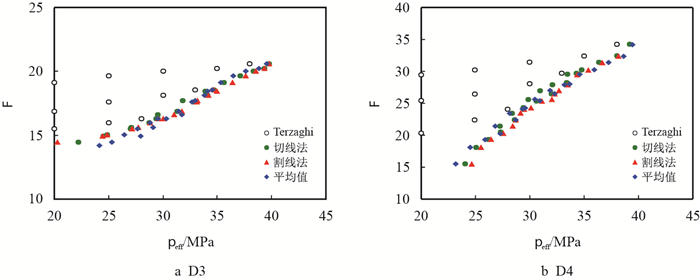 |
| 图6 有效应力系数不同取值时样本D3、D4地层因素与有效应力关系 Fig. 6 The effective pressure law for formation factor from the response-surface method applied to sample D3, D4 |
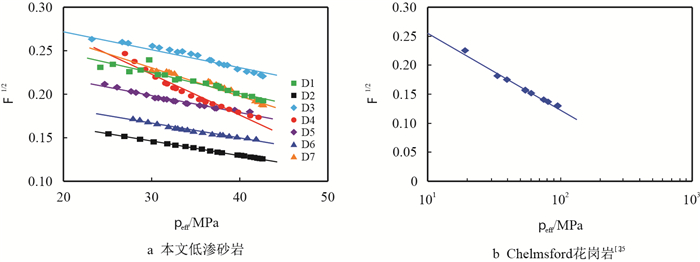
根据实验数据变化规律分析,为准确定量表征地层因素和有效应力之间的函数关系,基于数据分析结果拟合,认为地层因素和有效应力之间存在对数函数关系,表示为
 |
|
图7
|
理论研究将岩石导电视为骨架,固体颗粒表面液膜和微裂缝内流体导电的叠加,对于砂岩骨架,其电阻率相较于饱和流体已近绝缘,即电导率
| $ \dfrac{1}{R} = \dfrac{1}{R_{\text{s}}} + \dfrac{1}{R_{\text{c}}} + \dfrac{1}{R_{\text{m}}} = \sigma_{\text{s}} + \dfrac{1}{\rho_{\text{c}}}\dfrac{A_{\text{c}}}{l_{\text{e}}} + \dfrac{1}{R_{\text{m}}} $ | (6) |
式中:
由此可知,在忽略岩石骨架和孔喉内表面导电性条件下,微裂缝成为主要的电传导路径,则式(6)可近似表示为
| $ \left\{\begin{array}{l} F = \dfrac{\tau^{2}}{\phi}\\ K = \dfrac{r_{\text{H}}^{2}}{b}\dfrac{\phi}{\tau^{2}} \end{array}\right. $ | (7) |
式中:
式(7)将地层因素表示成为迂曲度与孔隙度的比值,并结合渗透率将地层因素与孔喉结构直接联系起来[36],模型将裂缝和孔喉截面近似为圆形或者椭圆形,并在实际研究中取得一定的应用效果。但该圆形和椭圆形分布孔喉结构并不具有广泛代表性,尤其对于微裂缝发育地层,裂缝面主要呈现锥形反面相切状接触。同时微裂缝的展布特征也使得应力作用下裂缝面的真实接触情况有必要进行考虑[37]。
结合扫描电镜分析认为,岩样中微裂缝截面分布如图 8所示,微裂缝横截面为接近真实的锥形状,电流传导路径与流体渗流路径是相同的。则有效应力作用下微裂缝面响应
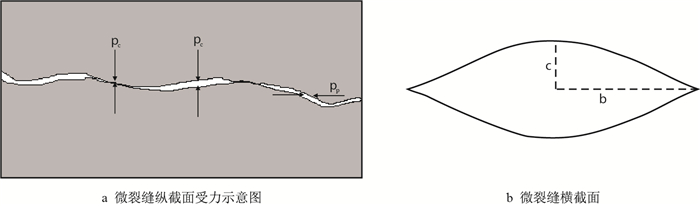 |
| 图8 微裂缝结构分布模型 Fig. 8 The structure model of the microfracture |
| $ \left\{\begin{array}{l} b (p_{\text{eff}}) = b_{0}{\left [1-\dfrac{4 (1-v^{2})}{3\varepsilon E} p_{\text{eff}}\right ]^{3/2}}\\ c (p_{\text{eff}}) = c_{0}{\left [1-\dfrac{4 (1-v^{2})}{3\varepsilon E} p_{\text{eff}}\right ]^{1/2}} \end{array}\right. $ | (8) |
式中:
当然,实际岩芯中微裂缝的纵横轴长度是变化的,不同位置的裂缝纵横轴长度并不相同,即
| $ \left\{\begin{array}{l} b (p_{\text{eff}}, x) = b_{0} (x){\left [1-\dfrac{4 (1-v^{2})}{3\varepsilon (x)E} p_{\text{eff}}\right ]^{3/2}}\\ c (p_{\text{eff}}, x) = c_{0} (x){\left [1-\dfrac{4 (1-v^{2})}{3\varepsilon (x)E} p_{\text{eff}}\right ]^{\text{1/2}}} \end{array}\right. $ | (9) |
此时,初始状态下微裂缝截面纵横比为
对于微裂缝,有效应力对水力半径(
| $ {\rm{d}}{r_{\rm{H}}} = - \sqrt 2 h{\rm{d}}{p_{{\rm{eff}}}}/{p_{{\rm{eff}}}} $ | (10) |
式中:
由式(7),可得
| $ F^{-1/2} = \sqrt{bK}/{r_{\text{H}}} $ | (11) |
基于逾渗理论
| $ K = C_{\rm{k}}{\left (\dfrac{r_{\text{H}}}{l}\right )^{2}}{\left (z-z_{\text{c}}\right )^{\beta}}r_{\text{H}}^{2} $ | (12) |
式中:
结合式(11)和式(12),得出
| $ F^{-1/2}=-\sqrt 2 h{(b{C_{\rm{k}}})^{-1/2}}{l^{-1}}{(z_{\text{f}}-z_{\text{cf}})^{\beta /2}} \ln p_{\text{eff}}+\\ {\hspace{4em}}F_{0}^{-1/2} $ | (13) |
则
| $ \left\{\begin{array}{l} A =-\sqrt 2 h{l^{-1}}{(b{C_{\rm{k}}})^{1/2}}{(z_{\text{f}}-z_{\text{cf}})^{\beta /2}}\\ B = F_{0}^{-1/2} = (b{C_{\rm{k}}})^{1/2}{l^{-1}}{r_{\text{H0}}}{(z_{\text{f0}}-z_{\text{cf0}})^{\beta /2}} \end{array}\right. $ | (14) |
式中:
式(14)表明,系数
同时,基于上述方法对Bernabé[25]的Chelmsford花岗岩实验数据进行分析,数据处理结果显示有效应力系数主要集中在0.735~1.043,割线法得到的有效应力与地层因素之间有良好的拟合效果,并呈现出明显的对数函数关系(图 7b所示),通过计算,得到系数
(1) 地层因素同围压(
(2) 采用响应面割线法计算得到的有效应力系数才能准确表征地层因素有效应力。有效应力系数(
(3) 微裂缝发育的低渗透砂岩储层,微裂缝作为主要导流路径,其分布和产状影响岩石导电性质,地层因素有效应力系数(
(4) 随着油田开发深入,有效应力的变化必然会导致地层因素发生相应变化,开发后期储层电性、含油性评价有必要考虑有效应力的影响。
| [1] |
ROBIN P Y F. Note on effective pressure[J]. Journal of Geophysical Research, 1973, 78(14): 2434-2437. doi: 10.1029/JB078i014p02434 |
| [2] |
江同文, 唐明龙, 肖香姣, 等. 塔里木盆地迪那2气田特低渗砂岩储层应力敏感性研究[J]. 沉积学报, 2007, 25(6): 949-953. JIANG Tongwen, TANG Minglong, XIAO Xiangjiao, et al. The study on stress sensitivity of the particular low permeability reservoir in Dina 2 Gas Field of Tarim Basin[J]. Acta Sedimentologica Sinica, 2007, 25(6): 949-953. doi: 10.3969/j.issn.1000-0550.2007.06.018 |
| [3] |
王瑞飞, 康楠, 吕新华, 等. 深层高压低渗砂岩油藏储层应力敏感性定量解释模型——以东濮凹陷文东油田沙三中油藏为例[J]. 地球物理学进展, 2013, 28(5): 2611-2617. WANG Ruifei, KANG Nan, LÜ Xinhua, et al. Quantitative model on stress sensitivity of sandstone reservoirs with deep section high pressure and low permeability:Taking the third member of Shahejie Formation in the Wendong Oil Field, Dongpu Sag, as an example[J]. Progress in Geophysics, 2013, 28(5): 2611-2617. doi: 10.6038/pg20130541 |
| [4] |
王厉强, 刘慧卿, 甄思广, 等. 低渗透储层应力敏感性定量解释研究[J]. 石油学报, 2009, 30(1): 96-99. WANG Liqiang, LIU Huiqing, ZHEN Siguang, et al. Quantitative research on stress sensitivity of lowpermeability reservoir[J]. Acta Petrolei Sinica, 2009, 30(1): 96-99. doi: 10.7623/syxb200901019 |
| [5] |
ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transaction of AIME, 1942, 146(3): 54-61. doi: 10.2118/942054-G |
| [6] |
WORTHINGTON P F. The uses and abuses of the archie equations, 1:The formation factor-porosity relationship[J]. Journal of Applied Geophysics, 1993, 30(3): 215-228. doi: 10.1016/0926-9851(93)90028-W |
| [7] |
SUMAN A, RUTH D. Formation factor and tortuosity of homogeneous porous media[J]. Transport in Porous Media, 1993, 12(2): 185-206. doi: 10.1007/BF00616979 |
| [8] |
代平, 孙良田, 李闽. 低渗透砂岩储层孔隙度、渗透率与有效应力关系研究[J]. 天然气工业, 2006, 26(5): 93-95. DAI Ping, SUN Liangtian, LI Min. Study on relation between porosity/permeability and effective stress of sand reservoir with low permeability[J]. Natural Gas Industry, 2006, 26(5): 93-95. doi: 10.3321/j.issn:1000-0976.2006.05.031 |
| [9] |
刘忠华, 吴淑琴, 杜宝会. 储层渗透性与地层因素关系的实验研究与分析[J]. 地球物理学报, 2013, 56(6): 2088-2097. LIU Zhonghua, WU Shuqin, DU Baohui, et al. Experimental study on the relationship between reservoir permeability and its formation resistivity factor[J]. Chinese Journal of Geophysics, 2013, 56(6): 2088-2097. doi: 10.60381/cjg20130629 |
| [10] |
BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. doi: 10.1063/1.1712886 |
| [11] |
BERNABÉ Y. The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks[J]. Journal of Geophysical Research Atmospheres, 1987, 92(B1): 649-657. doi: 10.1029/JB092iB01p00649 |
| [12] |
LI Min, XIAO Wenlian, BERNABÉ Y, et al. Nonlinear effective pressure law for permeability[J]. Journal of Geophysical Research:Solid Earth, 2014, 119(1): 302-318. doi: 10.1002/2013JB010485 |
| [13] |
肖文联, 李闽, 赵金洲, 等. 非线性有效压力计算[J]. 地球物理学报, 2013, 56(8): 2808-2817. XIAO Wenlian, LI Min, ZHAO Jinzhou, et al. Calculation of nonlinear effective pressure[J]. Chinese Journal of Geophysics, 2013, 56(8): 2808-2817. doi: 10.60381/cjg20130829 |
| [14] |
李传亮. 有效应力概念的误用[J]. 天然气工业, 2008, 28(10): 130-132. LI Chuanliang. Misusage of the concept of effective stress[J]. Natural Gas Industry, 2008, 28(10): 130-132. doi: 10.3787/j.issn.1000-0976.2008.10.041 |
| [15] |
周鹏高, 李亚双, 刘燕. 挤压作用形成异常高压的定量研究[J]. 西南石油大学学报(自然科学版), 2017, 39(3): 97-102. ZHOU Penggao, LI Yashuang, LIU Yan. Quantitative study on abnormal high pressure by extrusion effect[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(3): 97-102. doi: 10.11885/j.issn.1674-5086.2015.08.14.02 |
| [16] |
李闽, 肖文联, 赵春兰, 等. 不能用净应力评价低渗砂岩岩石应力敏感性[J]. 西南石油大学学报(自然科学版), 2009, 31(5): 183-186. LI Min, XIAO Wenlian, ZHAO Chunlan, et al. Net stress can not be used to evaluate the stress sensitivity in the low-permeability sandstone[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(5): 183-186. doi: 10.3863/j.issn.1674-5086.2009.05.041 |
| [17] |
卢家亭, 李闽. 低渗砂岩渗透率应力敏感性实验研究[J]. 天然气地球科学, 2007, 18(3): 339-341. LU Jiating, LI Min. Experimental research on permeability sensitivity of low-permeability sand rock[J]. Natural Gas Geoscience, 2007, 18(3): 339-341. doi: 10.3969/j.issn.1672-1926.2007.03.004 |
| [18] |
BRACE W F, ORANGE A S, MADDEN T R. The effect of pressure on the electrical resistivity of water-saturated crystalline rocks[J]. Journal of Geophysical Research, 1965, 70(22): 5669-5678. doi: 10.1029/JZ070i022p05669 |
| [19] |
BRACE W F. Some new measurements of linear compressibility of rocks[J]. Journal of Geophysical Research, 1965, 70(2): 391-398. doi: 10.1029/JZ070i002p00391 |
| [20] |
THOMAS N D. Permeability and electrical conductivity changes due to hydrostatic stress cycling of Berea and Muddy J Sandstone[J]. Journal of Geophysical Research:Solid Earth, 1986, 91(B1): 763-766. doi: 10.1029/JB091iB01p00763 |
| [21] |
FREDRICH J T, GREAVES K H, MARTIN J W. Pore geometry and transport properties of Fontainebleau sandstone[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(7): 691-697. doi: 10.1016/0148-9062(93)90007-Z |
| [22] |
ZISSER N, NOVER G. Anisotropy of permeability and complex resistivity of tight sandstones subjected to hydrostatic pressure[J]. Journal of Applied Geophysics, 2009, 68(3): 356-370. doi: 10.1016/j.jappgeo.2009.02.010 |
| [23] |
BERRYMAN J G. Effective stress for transport properties of inhomogeneous porous rock[J]. Journal of Geophysical Research:Solid Earth, 1992, 97(B12): 17409-17424. doi: 10.1029/92JB01593 |
| [24] |
BERRYMAN J G. Effective-stress rules for pore-fluid transport in rocks containing two minerals[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(7): 1165-1168. doi: 10.1016/0148-9062(93)90087-T |
| [25] |
BERNABÉ Y. Comparison of the effective pressure law for permeability and resistivity formation factor in chelmsford granite[J]. Pure and Applied Geophysics, 1988, 127(4): 607-625. doi: 10.1007/BF00881747 |
| [26] |
WARPINSKI N R, TEUFEL L W. Determination of the effective stress law for permeability and deformation in low-permeability rocks[C]. SPE 20572-PA, 1992. doi: 10.2118/20572-PA
|
| [27] |
TERZAGHI K. Principles of soil mechanics[J]. Engineering News-Record, 1925, 95: 987-996. |
| [28] |
HUBBERT M K, RUBEY W W. Role of fluid pressure in mechanics of overthrust faulting[J]. Geological Society of America Bulletin, 1959, 70(5): 115-166. doi: 10.1130/0016-7606(1959)70[115:ROFPIM]2.0.CO;2 |
| [29] |
DAILY W D, LIU W. Laboratory-determined transport properties of Berea sandstone[J]. Geophysics, 1985, 50(5): 775-784. doi: 10.1190/1.1441952 |
| [30] |
REVIL A, CATHLES L M, LOSH S, et al. Electrical conductivity in shaly sands with geophysical applications[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B10): 23925-23936. doi: 10.1029/98JB02125 |
| [31] |
白斌, 朱如凯, 吴松涛, 等. 利用多尺度CT成像表征致密砂岩微观孔喉结构[J]. 石油勘探与开发, 2013, 40(3): 329-333. BAI Bin, ZHU Rukai, WU Songtao, et al. Multi-scale method of nano (Micro)-CT study on microscopic pore structure of tight sandstone of Yanchang Formation, Ordos Basin[J]. Petroleum Exploration and Development, 2013, 40(3): 329-333. doi: 10.11698/PED.2013.03.09 |
| [32] |
巩磊, 高铭泽, 曾联波, 等. 影响致密砂岩储层裂缝分布的主控因素分析——以库车前陆盆地侏罗系新近系为例[J]. 天然气地球科学, 2017, 28(2): 199-208. GONG Lei, GAO Mingze, ZENG Lianbo, et al. Controlling factors on fracture development in the tight sandstone reservoirs:A case study of Jurassir-Neogene in the Kuqa Foreland Basin[J]. Natural Gas Geoscience, 2017, 28(2): 199-208. doi: 10.11764/j.issn.1672-1926.2016.12.003 |
| [33] |
王明培, 陈猛, 李闽, 等. 有效应力作用下岩石渗透性和电性响应特征[J]. 西南石油大学学报(自然科学版), 2017, 39(3): 85-96. WANG Mingpei, CHEN Meng, LI Min, et al. Permeability and electrical response characteristics of rocks under effective stress[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(3): 85-96. doi: 10.11885/j.issn.1674-5086.2016.05.26.03 |
| [34] |
李乐忠, 李相方. 储层应力敏感实验评价方法的误差分析[J]. 天然气工业, 2013, 33(2): 48-51. LI Lezhong, LI Xiangfang. Error analysis of experimental evaluation methods for stress sensitivity of reservoirs[J]. Natural Gas Industry, 2013, 33(2): 48-51. doi: 10.3787/j.issn.1000-0976.2013.02.010 |
| [35] |
PATERSON M S. The equivalent channel model for permeability and resistivity in fuid-saturated rock-A reappraisal[J]. Mechanics of Materials, 1983, 2(4): 345-352. doi: 10.1016/0167-6636(83)90025-X |
| [36] |
WALSH J B, BRACE W F. The effect of pressure on porosity and the transport properties of rocks[J]. Journal of Geophysical Research, 1984, 89(B11): 9425-9431. doi: 10.1029/JB089iB11p09425 |
| [37] |
BROWN S R, SCHOLZ C H. Closure of random elastic surfaces in contact[J]. Journal of Geophysical Research, 1985, 90(B7): 5531-5545. doi: 10.1029/JB090iB-07p05531 |
| [38] |
BERNABÉ Y, LI Min, MAINEULT A. Permeability and pore connectivity:A new model based on network simulations[J]. Journal of Geophysical Research:Solid Earth, 2010, 115(B10): 1-14. doi: 10.1029/2010JB007444 |
 2019, Vol. 41
2019, Vol. 41


