2. 中国石化西南油气分公司勘探开发研究院, 四川 成都 610041
2. Exploration and Production Research Institute, Southwest Oil and Gas Company, SINOPEC, Chengdu, Sichuan 610041, China
纵、横波速比(
基于Sinc插值算法的
由于转换横波速度低于纵波速度,因此,同一反射层在转换波剖面和纵波剖面上的到达时间是不一致的。对于某一深度为
| $ \frac{h}{{{v_{{\rm{P0}}}}}} + \frac{h}{{{v_{{\rm{S0}}}}}} = {t_{{\rm{PS0}}}} $ | (1) |
| $ \frac{{2h}}{{{v_{{\rm{P0}}}}}} = {t_{{\rm{PP0}}}} $ | (2) |
式中:
由式(1)、式(2)可以得到
| $ {t_{{\rm{PS0}}}} = \dfrac{{1 + \dfrac{{{v_{{\rm{P0}}}}}}{{{v_{{\rm{S0}}}}}}}}{2}{t_{{\rm{PP0}}}} $ | (3) |
令
| $ {t_{{\rm{PS0}}}} = \dfrac{{1 + {\gamma _0}}}{2}{t_{{\rm{PP0}}}} $ | (4) |
式中:
式(4)为将纵、横波速度比转化为时间比的公式。
如果给定一个
设有函数
| $ f(x) = \sum\limits_i {{f_{\rm{d}}}(i) * \sin c(x - i)} $ | (5) |
式(5)可以看成是
Sinc插值方法得到的插值结果是无偏的[2],而且比起较为精确的拉格朗日插值方法而言在相同阶数的情况下其计算量要小。因此,从计算量和插值精度来说,Sinc插值方法是一种进行信号插值的良好方法。
图 1为采样间隔2 ms、21个采样点、主频30 Hz的雷克子波,对该子波进行1.5倍拉伸后采样间隔变为3 ms。用Sinc插值算法插值后子波为32个采样点,采样间隔还原为2 ms。从图 1可以看出,Sinc插值算法可以在保持原始波形不变的情况下,很好地对拉伸或压缩后地震道数据的采样间隔进行还原。
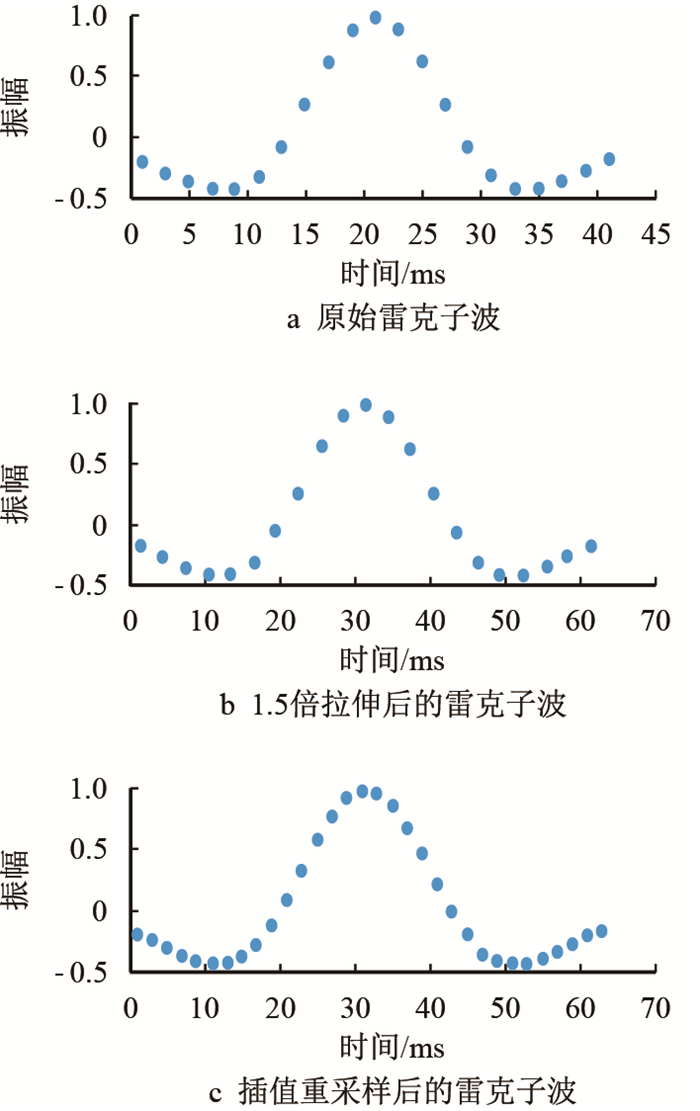 |
| 图1 雷克子波的Sinc插值重采样 Fig. 1 Resampling of Sinc-interpolation of Ricker wavelet |
在地球物理模型建立和反演中有许多共轭运算符,如:褶积和反褶积、拉伸和压缩、绕射模型和偏移。在纵、横波速比扫描方法中,共轭运算符为拉伸纵波到转换波时间及压缩转换波到纵波时间[4]。首先,选取第
| $ b_i^{'} = \Gamma {b_i} $ | (6) |
式中:
因此,式(6)可写为
| $ \mathop {b_i^{'}}\limits^{} ({\gamma _{{\rm{avg}}}}) = \Gamma ({\gamma _{{\rm{avg}}}})b_i $ | (7) |
用一系列的
| $ {c_k}({\gamma _{{\rm{avg}}}}) = \sum\limits_{i = k - l/2}^{k + l/2} {{a_i}b_i^{'}({\gamma _{{\rm{avg}}}})} $ | (8) |
式中:
当用正确的
为验证基于Sinc插值算法的纵横波速比值扫描方法的有效性,采用数值模拟方法构建了一个P波CMP叠加剖面和一个PS波CCP叠加剖面进行计算。P波的CMP叠加剖面数据时长1 s,采样率为2 ms,在0.1~0.9 s处有反射层位,反射系数在奇数层位为正,偶数层位为负。地震子波为35 Hz的雷克子波,子波时长60 ms(图 2a)。
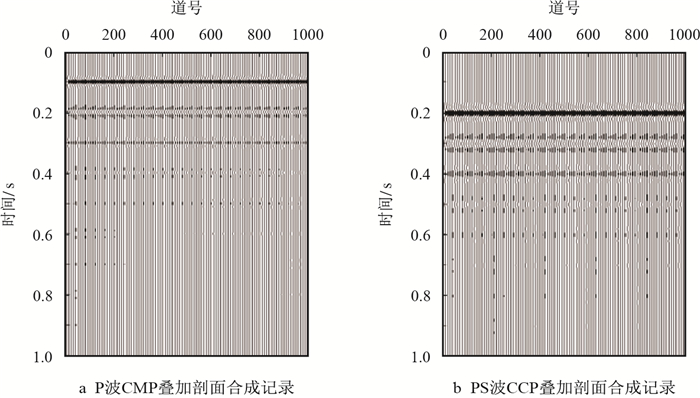 |
| 图2 理论试验模型 Fig. 2 Therotical model of experiment |
PS波的CCP叠加剖面数据时长1 s,采样率为2 ms,在0.2~0.9 s处有反射层位,反射系数在偶数层位为正,奇数层位为负。地震子波为20 Hz的雷克子波,子波时长60 ms,如图 2b所示。两者的振幅值都做了衰减处理以模拟真实的情况。
图 3是用基于Sinc插值算法的
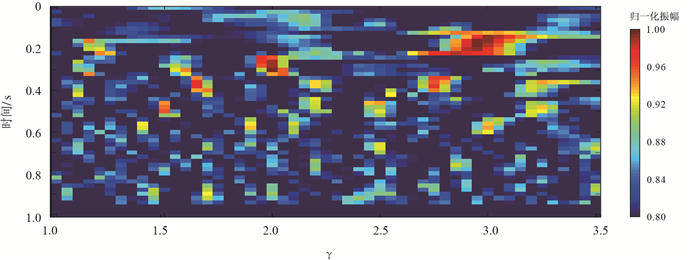 |
|
图3
基于Sinc插值的 |
|
表1 扫描得到的 |
从表 1可以看出,扫描得到的
为验证该方法的实用性,针对川西地区转换波地震勘探资料用该方法进行
 |
| 图4 川西某工区纵波CMP叠加剖面 Fig. 4 P-wave seismic data in western Sichuan |
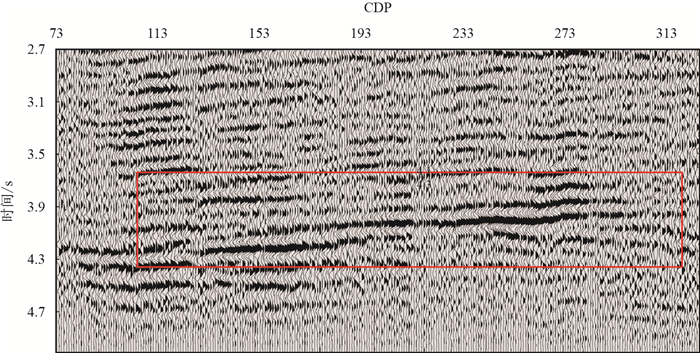 |
| 图5 川西某工区转换波ACCP叠加剖面 Fig. 5 PS-wave seismic data in western Sichuan |
图 6a是扫描得到的互相关系数谱,得到转换波时间3.50~4.35 s的
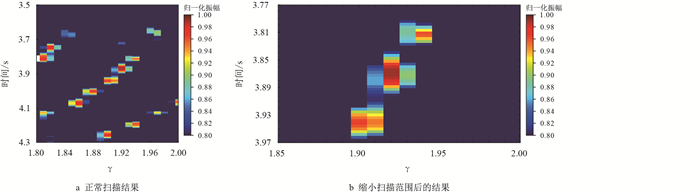 |
|
图6
扫描得到的互相关系数谱
Fig. 6
Cross-correlation spectrum by |
|
表2 实际资料 |
基于Sinc插值的纵、横波速比值扫描方法从纵、横波速比与时间比的关系入手,利用Sinc插值算法对拉伸后的纵波地震道进行重采样,从扫描出的互相关系数谱中得到纵、横波速比。理论模型试验和实际资料处理证明,该方法能得到较为准确的纵、横波速比,是一种有效的、实用的纵横波速比扫描方法。
| [1] |
BEHLE A, DOHR G. Converted waves in exploration seismic[M]. Seismic shear waves: Part B-Applications Geophys, 1985: 178-223.
|
| [2] |
MCCORMACK M D. Detection of subsurface anisotropy: US: 4947381[P]. 1990.
|
| [3] |
SCHANZE T. Sinc interpolation of discrete periodic signals[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1502-1503. doi: 10.1109/78.388863 |
| [4] |
黄绪德, 杨文霞. 转换波地震勘探[M]. 北京: 石油工业出版社, 2008.
|
| [5] |
黄中玉, 孙建库, 朱仕军, 等. 多分量地震技术[M]. 北京: 石油工业出版社, 2007.
|
| [6] |
唐建明, 马昭军. 宽方位三维三分量地震资料采集观测系统设计——以新场气田三维三分量勘探为例[J]. 石油物探, 2007, 46(3): 310-318. TANG Jianming, MA Zhaojun. Design of wide-azimuth 3D3C seismic data acquisition geometry:Case study of 3D3C exploration in Xinchang Gas Field[J]. Geophysical Prospecting for Petroleum, 2007, 46(3): 310-318. doi: 10.3969/j.issn.1000-1441.2007.03.014 |
| [7] |
马昭军, 唐建明, 杨振武. 三维转换波处理方法研究与应用[J]. 天然气工业, 2007, 27(S1): 213-215. |
| [8] |
甘其刚, 许多. 川西深层致密碎屑岩气藏储层预测方法[J]. 石油物探, 2008, 47(6): 593-597. GAN Qigang, XU Duo. Prediction of gas reservoir deeply buried tight clastic rock in west Sichuan[J]. Geophysical Prospecting for Petroleum, 2008, 47(6): 593-597. doi: 10.3969/j.issn.1000-1441.2008.06.009 |
| [9] |
徐天吉, 程冰洁, 唐建明. PP波与P-SV波叠前联合反演研究与应用[J]. 勘探地球物理进展, 2008, 31(5): 368-372. XU Tianji, CHENG Bingjie, TANG Jianming. Prestack PP and P-SV wave joint inversion and its application[J]. Progress in Exploration Geophysics, 2008, 31(5): 368-372. |
| [10] |
洪余刚, 李亚林, 李忠, 等. 多分量地震资料层位对比[J]. 天然气工业, 2008, 28(9): 41-43. HONG Yugang, LI Yalin, LI Zhong, et al. Consistent matching by the multicomponent seismic method[J]. Natural Gas Industry, 2008, 28(9): 41-43. doi: 10.3787/j.issn.1000-0976.2008.09.011 |
| [11] |
黄东山, 谢芳, 梁波, 等. 转换波层位标定对比技术在川中GA构造中的应用[J]. 天然气工业, 2007, 27(S1): 225-227. |
| [12] |
马昭军, 唐建明, 吕其彪. 三维转换波处理技术在新场地区的应用[J]. 新疆石油地质, 2008, 29(3): 376-379. MA Zhaojun, TANG Jianming, LÜ Qibiao. Application of 3D converted wave processing to Xinchang Area[J]. Xinjiang Petroleum Geology, 2008, 29(3): 376-379. |
| [13] |
唐建侯, 李亚林, 杜文军, 等. 山地转换波资料处理技术的进展[J]. 天然气工业, 2003, 23(3): 137-139. doi: 10.3321/j.issn:1000-0976.2003.03.045 |
| [14] |
马昭军, 唐建明. 基于构造时间控制的P-SV波静校正方法[J]. 物探化探计算技术, 2008, 30(5): 373-376. MA Zhaojun, TANG Jianming. A P-SV wave static correction method based on controlling structure time[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(5): 373-376. doi: 10.3969/j.issn.1001-1749.2008.05.006 |
| [15] |
吴波, 潘树林, 陈辉. 用四阶累积子函数计算剩余静校正量[J]. 石油物探, 2010, 49(3): 227-231. WU Bo, PAN Shulin, CHEN Hui. Improvement of calculation residual statics by fourth-order cumulant subfunction[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 227-231. doi: 10.3969/j.issn.1000-1441.2010.03.003 |
| [16] |
吴波, 尹成, 潘树林, 等. 最大能量法剩余静校正的改进[J]. 石油地球物理勘探, 2010, 45(3): 350-354. WU Bo, YIN Cheng, PAN Shulin, et al. The improvements on maximum energy method residual static correction[J]. Oil Geophysical Prospecting, 2010, 45(3): 350-354. doi: 10.13810/j.cnki.issn.1000-7210.2010.03.007 |
| [17] |
吴波, 徐天吉, 唐建明, 等. 三种反射剩余静校正方法对比应用[J]. 石油物探, 2012, 51(2): 172-177. WU Bo, XU Tianji, TANG Jianming, et al. The comparison and application of three reflection residual static correction methods[J]. Geophysical Prospecting for Petroleum, 2012, 51(2): 172-177. doi: 10.3969/j.issn.1000-1441.2012.02.010 |
 2019, Vol. 41
2019, Vol. 41


