2. 中国石油西南油气田分公司通信与信息技术中心, 四川 成都 610051
2. Communication and Information Technology Center of PetroChina Southwest Oil and Gas Field Branch Company, Chengdu, Sichuan 610051, China
钻井液设计是钻井工程中的重要组成部分,科学合理的钻井液设计可以避免或减少井漏、井喷、井塌等井下事故的发生,保证钻井工作的顺利进行。现阶段,钻井液设计工作主要是依靠专业人员的设计经验,并综合大量的数据和实验来完成的。这种传统的设计方法使大量的钻井经验数据得不到有效地保存,钻井液领域的专家知识得不到有效地吸收和利用[1]。为提高钻井的工作效率和经济性,实现钻井液设计的信息化和智能化,将案例推理技术运用于钻井液设计过程中。
案例推理(CBR:Case-Based Reasoning)是20世纪80年代人工智能领域兴起的一个重要的推理技术,是一种根据过去类似问题的求解经验解决新问题的方法[2]-[4]。目前,CBR在很多领域已经取得了阶段性的成果,如钻井液优化设计[5]、疾病预测[6]、分类与诊断[7]等。基于CBR的钻井液设计是将智能化技术运用于钻井工作的有益尝试,根据岩性、井型、井深等条件,对一口井所使用的钻井液体系进行快速合理的选择,提高了钻井液设计的效率。但案例的属性权重多由专家根据经验给出,权值不能很好地确定,会对推理结果的正确与否产生显著的影响。
现阶段,确定属性权重的方法包括专家赋权法[8]、相关分析法[9]、层次分析法[10]等类型的主观赋权法,以及粒子群算法[11]、模拟退火算法[12]、遗传算法等类型的客观赋权法。特别地,在属性权重分配问题上,遗传算法已经得到了广泛的关注。付雅芳等提出利用遗传算法进行相似项目选取和特征权重优化,提高了软件费用的估算精度[13];王丽敏等提出利用遗传算法优化属性权重,提高了分类的正确率[14];李海芳等提出了一种基于遗传算法的全局优化案例检索模型,提高了案例的检索效率[15]。在属性权重分配问题上,遗传算法作为一种全局搜索优化算法,具有较强的鲁棒性和全局优化能力,但也存在收敛速度慢和优化精度低的缺点[16]。
针对传统遗传算法的不足,本文提出一种改进的遗传算法(IGA:Improved Genetic Algorithm):在传统遗传算法的基础上,从个体适应度和交叉个体的差异程度两方面实现交叉概率自适应调节,改善了算法的全局收敛性能;利用自适应遗传算子对遗传算法进行改进:选择算子方面,利用指数尺度变换法对适应度函数进行缩放,在一定程度上克服了算法的早熟现象;交叉算子方面,自适应调整比例因子,避免了算术交叉过程的盲目性;变异算子方面,改进个体的变异方向,增强了算法的搜索能力。
利用改进的遗传算法对UCI数据集进行测试,验证了方法的可行性和有效性,并将其运用到基于CBR的钻井液设计中,对CBR模型中的属性权重进行优化,实验结果表明本文方法能有效提高钻井液设计的质量。
1 基于CBR的钻井液设计专家系统 1.1 CBR技术概述CBR包括案例检索、案例重用、案例修正和案例存储4个阶段,其基本原理如图 1所示:首先提取新问题的特征形成目标案例,然后从历史案例库中检索出与目标案例完全或近似匹配的一条或多条案例,评价相似案例,如果相似案例完全满足目标案例的要求,则重用相似案例的解,否则,根据目标案例的要求,修改相似案例的解,最后将目标案例与其对应的解作为一条新的案例保存到历史案例库中,实现案例库的动态更新。
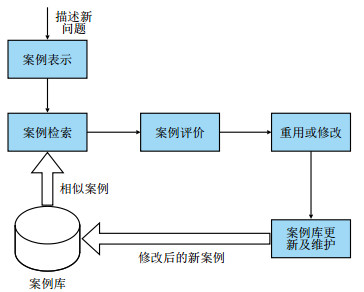 |
| 图1 CBR推理流程图 Fig. 1 CBR reasoning flow chart |
CBR是一种相似问题求解方法,它符合钻井液设计领域专家的思维过程。CBR技术运用于钻井液设计过程中具有很好的推广价值,不仅可以有效地保存钻井液设计领域的宝贵经验和专家知识,而且通过井的一些基本信息就可以快速地从案例库中检索出适合的钻井液体系,优化了钻井液的设计过程。
1.2 钻井液体系的案例表示通过分析钻井液设计过程中的相关数据,对这些数据进行整理、归纳,并提取关键信息,利用这些信息表示一条钻井液体系案例。基于CBR的钻井液设计中,通过井的基本信息在钻井液体系案例库中进行匹配得到最适合该井的钻井液体系。一条钻井液体系案例应该包括“井型”、“井别”、“井段”、“开钻次序”、“井深”、“岩性”、“复杂情况”7个条件属性,以及由这些条件属性推理得到的钻井液体系,案例的集合构成了案例库。文献[17]中,案例库
| $ S = \left\{ {({\mathit{\boldsymbol{x}}_j},{y_j})|1 \leqslant j \leqslant n} \right.\left. {{\rm{, }}({\mathit{\boldsymbol{x}}_j}) \in {{{\mathit{\boldsymbol{R}}} }^m} \times {{\mathit{\boldsymbol{R}}} }} \right\} $ | (1) |
式中:
钻井液数据是混合型数据集,包含了数值型、符号型、多值符号型和区间型的数据。对于数值型和区间型属性,由于度量单位的不同,在进行相似度计算前,应对其进行归一化处理。
特别地,多值符号型属性如“岩性”、“复杂情况”通常取值域中的一种或多种值。在这种情况下,编码后的位数不变,若属性值为值域中的一种或多种,则其对应位置的编码为1,其余位为0。如“岩性”属性取值为“砂岩”,“泥页岩”,“碳酸岩”,则其编码为“1101”。
1.3 钻井液体系的检索钻井液设计过程中,不同条件属性对钻井液体系选择的影响是不同的,需要根据其影响程度为这些条件属性分配权重,以确保钻井液体系选择的正确性。案例检索根据目标案例的属性权重及属性值,从历史案例库中检索出一个或一组与其相似的历史案例。案例检索算法采用K-最近邻法[18],将目标案例
| ${\rm{sim}}\left( {{x_{\rm{t}}}, {x_i}} \right) = \sum\limits_{k = 1}^m {{w_k}{\rm{sim}}_k({x_{\rm{t}}}, {x_i})} $ | (2) |
式中:
根据式(2)可知,案例之间的相似度是各属性相似度的加权求和。钻井液数据是混合型属性数据,不同类型的属性相似度采用不同的相似度计算方法。
(1) 对于数值型属性,利用欧式距离法求得案例之间的距离,经转换后可得该属性的相似度
| ${\rm{sim}}{_k}({x_{\rm{t}}}, {x_i}){\rm{ = }}\dfrac{1}{{{\rm{dist(}}{{{x}}_{{\rm{t}}k}}, {x_{ik}}{\rm{) + 1}}}} $ | (3) |
式中:
| $ {\rm{dist(}}{x_{{\rm{t}}k}}, {x_{ik}}{\rm{) = }}\left| {{x_{{\rm{t}}k}} - {x_{ik}}} \right| $ | (4) |
(2) 对于符号型属性,定义如下
| ${\rm{sim}}{_k}({x_t}, {x_i}){\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {1\begin{array}{*{20}{l}} , &{\begin{array}{*{20}{l}} {} \end{array}{x_{tk}} = {x_{ik}}} \end{array}}\\ {0\begin{array}{*{20}{l}} , &{\begin{array}{*{20}{l}} {} \end{array}{x_{tk}} \ne {x_{ik}}} \end{array}} \end{array}} \right. $ | (5) |
(3) 对于多值符号型属性,可利用Jaccard相似性系数法计算相似度。两个多值符号型属性值
| ${\rm{sim}}(A, B){\rm{ = }}\dfrac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}} $ | (6) |
(4) 对于区间型属性,假设目标案例
| ${\rm{sim}}(M, N)\!=\!L(M \cap N)/\left[ {L(M)\!+\!L(N)\!-\!L(M \cap N)} \right] $ | (7) |
式中:
在式(2)中,属性权重的分配决定了案例之间的相似度大小,进而对推理结果的正确与否产生显著的影响。针对传统遗传算法在解决属性权重分配问题时所存在的缺点,本文提出一种改进的遗传算法。
2 改进的遗传算法遗传算法是John Holland于1975年受达尔文生物进化论的启发而提出来的一种全局搜索优化算法[19],它是人工智能领域的一个重要分支。针对遗传算法在属性权重分配问题上存在的收敛速度慢和优化精度低的缺点,本文提出一种改进的遗传算法。
2.1 编码及适应度函数选择为提高遗传算法的计算效率和精度,对各个属性采用实数编码的方式,将编码后的每组权值表示为种群中的一个个体
| ${w_i} = ({w_{i1}}, {w_{i2}}, ..., {w_{ik}}, ..., {w_{im}}) $ | (8) |
式中:
考虑到案例检索算法采用
| ${f_i} = \dfrac{1}{n}\sum\limits_{i = 1}^n {I\left( {{y_{\rm{a}}} = {y_{\rm{p}}}} \right)} $ | (9) |
式中:
赌轮盘选择算子按照与个体适应度成正比的方法决定当前种群中每个个体被选择机会的大小[20],个体
| $ \left\{ {\begin{array}{*{20}{c}} {{p_i} = \dfrac{{{f_i}}}{{\sum\limits_{k = 1}^N {{f_k}} }}}\\ {{Q_i} = \sum\limits_{j = 1}^i {{p_j}} } \end{array}} \right. $ | (10) |
式中:
取随机数
随着进化代数的增加,赌轮盘选择方法使得优良个体可能被多次选择,导致参与交叉运算的父代群体的多样性过低,算法容易早熟。因此,本文提出利用指数尺度变换法对适应度函数进行拉伸,可以在一定程度上消除遗传算法的早熟现象。指数尺度变换法使得算法在进化的初始阶段,缩小个体之间的适应度差异,以维护种群的多样性;在进化的后期阶段,将适应度的差异放大,使优良个体的表现更加突出。适应度函数被拉伸后,个体
| $p{'_i} = \dfrac{{{\rm e}^{{0.5g{f_i}/G}}}}{\sum\limits_{k = 1}^N {{{\rm e}^{{0.5g{f_k}/G}}}}} $ | (11) |
式中:
随着迭代次数
为了保证优良的基因结构得以延续,引入精英保留策略,即始终保留进化过程中的历史最优个体
为加快种群的更新速度,本文采用多点不连续交叉算子优化交叉结果。按交叉概率
| $u_i{'} = \alpha {u_i} + (1 - \alpha ){v_i} $ | (12) |
| $v_i{'} = \alpha {v_i} + (1 - \alpha ){u_i} $ | (13) |
式中:
| $\alpha {\rm{ = }}\dfrac{{{{\rm{e}}^{ - \beta {f_{\rm{u}}}}}}}{{{{\rm{e}}^{ - \beta {f_{\rm{u}}}}} + {{\rm{e}}^{ - \beta {f_{\rm{v}}}}}}} $ | (14) |
式中:
利用指数尺度变换法对个体的适应度进行拉伸,
变异算子通常对变异个体的变异位置取随机值,这种方式带有很大的盲目性,算法不一定收敛到全局最优解。为增强遗传算法的搜索能力,采用改进的变异算子:设个体
| $u_i{'} = \left\{ {\begin{array}{*{20}{l}} {{u_i} + {r_1}(w_{\rm{{best}}}^i - {u_i})}\\ {{r_2}} \end{array}\begin{array}{*{20}{l}} \\ {} \end{array}\begin{array}{*{20}{r}} {\begin{array}{*{20}{l}} {} \end{array}r_3 < 0.5}\\ {\begin{array}{*{20}{l}} {} \end{array}r_3 \geqslant 0.5} \end{array}} \right. $ | (15) |
式中:
改进变异算子既能通过随机取值的方式扩大个体的搜索范围,又能使种群朝着最优的方向进化,以增强算法的局部搜索能力。
2.5 自适应交叉和变异概率在遗传算法中,交叉概率
| ${\mathit{p}_{\rm{c}}} = \left\{ \begin{array}{l} {\mathit{p}_{{\rm{c1}}}} - \frac{{\left( {{p_{{\rm{c1}}}} - {p_{{\rm{c2}}}}} \right)\left( {{f_{{\rm{bigger}}}} - {f_{{\rm{av}}}}} \right)}}{{\left( {{f_{\max }} - {f_{{\rm{av}}}}} \right)}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{f}_{bigger}} \ge {\mathit{f}_{{\rm{av}}}}, {f_{\max }} > {f_{{\rm{av}}}}\\ {p_{{\rm{c1}}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}} \end{array} \right. $ | (16) |
| ${\mathit{p}_{\rm{c}}} = \left\{ \begin{array}{l} {p_{{\rm{m1}}}} - \frac{{\left( {{p_{{\rm{m}}1}} - {p_{{\rm{m2}}}}} \right)\left( {f - {f_{{\rm{av}}}}} \right)}}{{\left( {{f_{{\rm{max}}}} - {f_{{\rm{av}}}}} \right)}}, {\rm{\;\;\;\;\;\;\;\;}}f \ge {f_{{\rm{av}}}}, {f_{{\rm{max}}}} > {f_{{\rm{av}}}}\\ {p_{{\rm{m3, }}}}{\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}{f_{{\rm{max}}}} = {f_{{\rm{av}}}}\\ {p_{{\rm{m1}}}}, {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}{其他} \end{array} \right. $ | (17) |
式中:
式(17)中,交叉概率能随个体适应度及种群的分散程度动态的调整大小,但并未考虑到参与交叉运算的两个父个体之间的适应度差异。因此,本文对式(17)做进一步改进,认为父代个体的适应度差异越大,交叉概率
| ${p_{\rm{c}}} = \left\{ \begin{array}{l} {p_{{\rm{c2}}}} + \left( {{p_{{\rm{c1}}}} - {p_{{\rm{c2}}}}} \right)\left[ {\frac{{f - {f_{{\rm{av}}}}}}{{2\left( {{f_{{\rm{max}}}} - {f_{{\rm{av}}}}} \right)}} + \frac{{\left| {{f_{\rm{1}}} - {f_2}} \right|}}{{2\left( {{f_1} + {f_2}} \right)}}} \right],\;\;\;\;\;\;\;\;\;\;\;\;f \ge {\mathit{f}_{{\rm{av}}}},{f_{{\rm{max}}}} > {f_{{\rm{av}}}}\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{max}}}} = {f_{{\rm{av}}}}\\ {p_{{\rm{c1}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}} \end{array} \right. $ | (18) |
式中:
定义
在CBR分类器中,利用改进的遗传算法解决属性权重的分配问题,其步骤如下。
步骤1:初始参数设置
设定遗传算法的种群规模为
步骤2:属性权重计算
(1) 根据初始种群得到初始的案例属性权重,并根据式(9)计算个体适应度。
(2) 根据式(11)和式(10)计算每个个体的被选择概率
(3) 根据式(18)计算所选取个体的交叉概率
(4) 利用式(17)计算交叉后个体的变异概率
(5) 判断算法是否满足收敛条件或达到最大迭代次数,若满足,则输出最优个体及其对应的属性权重
步骤3:将优化后的属性权重
(1) 将
(2) 根据
在CBR模型中,为考察改进遗传算法在优化属性权重上的有效性,设计了以下3种方法的分类实验。
(1) 利用均权法(EW)分配属性权重的CBR分类器,记为EW-CBR;
(2) 利用传统遗传算法(GA)优化属性权重的CBR分类器,记为GA-CBR;
(3) 利用改进的遗传算法(IGA)优化属性权重的CBR分类器,记为IGA-CBR。
实验参数设置:种群规模
采用分类准确率作为3种方法的性能指标函数,并在方法的收敛精度和收敛速度上,对GA和IGA算法做对比实验。分类准确率
| $A = \dfrac{{P + Q}}{{P + R + S + Q}} \times 100{\rm{\% }} $ | (19) |
式中:
为了验证本文所提方法的有效性及性能,选取UCI(University of California Irvine)资源库中的5组数据集进行测试,分别是SH(Statlog Heart)、WQR(Wine Quality Red)、IS(Image Segmentation)、SPF(Steel Plates Faults)、VS(Vehicle Silhouettes)。为了考察属性权重的分配对CBR分类器的影响,每组数据集均采用3种CBR分类器,分别为EW-CBR、GA-CBR和IGA-CBR。为保证结果的客观性,利用五折交叉验证实验来验证方法的有效性。3种分类器对各组数据集的平均分类准确率见表 2和图 2。
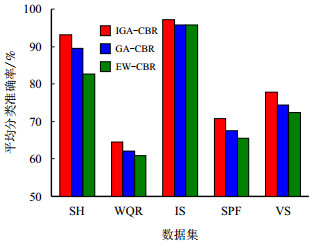 |
| 图2 不同数据集的平均分类准确率 Fig. 2 Average classification accuracy of different data sets |
| 表2 不同数据集的平均准确率 Tab. 2 Average classification accuracy of different data sets |
5组UCI数据集测试结果表明,在同等情况下,IGA-CBR的分类精度要高于GA-CBR和EW-CBR,使用改进的遗传算法能提高分类精度。
以SH(Statlog Heart)数据集为例,记录利用GA和IGA两种方法对CBR分类器的属性权重进行迭代调整时分类准确率的变化情况,结果如图 3。
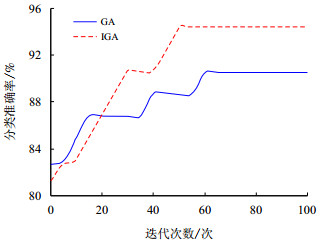 |
| 图3 迭代调整时数据集的分类准确率 Fig. 3 Accuracy of data sets during iterative adjustment |
从图 3可以看出,在最大迭代次数相同的情况下,改进的遗传算法IGA能够使CBR分类器达到更高的精度,且收敛速度更快。这表明改进的遗传算法可以改善传统遗传算法的全局收敛性能,提高CBR分类的准确率。
3.3 钻井液数据集实验钻井液是钻井过程中以其多种功能满足钻井工作需要的循环流体,是钻井工程中的重要组成部分,决定了钻井工作能否顺利完成。表 3为利用表 1方法经编码后所得到的部分钻井液实例,其中,属性分别为井型(JX)、井别(JB)、井段(JD)、开钻次序(KZCX)、井深(JS)、岩性(YX)、复杂情况(FZQK)。
| 表1 编码映射表 Tab. 1 Coding mapping table |
| 表3 不同数据集的平均准确率 Tab. 3 Average classification accuracy of different data sets |
钻井液体系的种类随着具体要求和钻井液技术的进步而逐渐增多,1990年,中国钻井液标准化分委会[22]根据体系组成特点和流体介质的不同,将钻井液分成了8大体系,即0——黏土原浆钻井液、1——分散钻井液、2——钙处理钻井液、3——盐水钻井液、4——聚合物钻井液、5——完井液体系、6——油基钻井液体系、7——气基体系。
对表中3的JS、JD属性值进行归一化处理后,分别采用均权法、遗传算法和改进的遗传算法优化属性权重,采用IGA-CBR对钻井液的体系做分类测试,并与EW-CBR、GA-CBR作对比。此外,为了更加精准地对结果进行评价,根据经验,对钻井液体系案例的各个属性权重赋值:
对IGA-CBR,分别取不同的
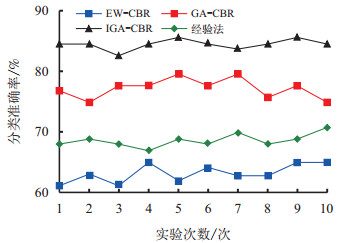 |
| 图4 分类结果折线图 Fig. 4 Line chart of classification results |
| 表4 钻井液数据分类结果 Tab. 4 Classification results of drilling fluid data |
从表 4和图 4可以看出,在分类准确率上,GA、IGA和经验法都要比均权法高,这就表明了合理的权重分配结果会提高钻井液体系分类的精度,证明了遗传算法在权重分配上的有效性,能够提高CBR分类器的可靠性。经验法的分类精度虽优于均权法,但明显低于遗传算法,这说明专家根据经验给定的权重具有一定的合理性,但其值不能很好地确定,优化效果仍不理想。IGA-CBR的分类精度约为84.37%,高于GA-CBR,这表明本文所提方法在提高案例推理准确率方面较传统遗传算法更有优势性。将IGA-CBR用于钻井液设计中可以提高钻井体系选择的准确率,进而提高钻井液设计的质量。
4 结论(1) 在基于CBR的钻井液设计中,考虑到属性权重的分配会对推理结果产生显著的影响,提出了一种解决CBR中属性权重分配问题的改进遗传算法。
(2) 在传统遗传算法的基础上对选择算子、交叉算子和变异算子3种遗传算子进行改进;并从个体适应度和交叉个体的差异程度两方面实现交叉概率自适应调节。标准UCI数据集的实验结果证明了改进后的遗传算法具有收敛速度快,收敛精度高的优点。
(3) 将该算法用于基于CBR的钻井液设计中可以优化属性权重的分配,从而快速合理地获得一口井所适合的钻井液体系,提高了钻井液设计的质量。下一步研究的重点在于利用该方法对钻井液配方设计过程进行优化,以提高钻井液配方的设计效率。
| [1] |
胡庆辉, 赵正文, 陆玉靖. 钻井液专家系统的研究与设计[J]. 钻井液与完井液, 2007, 24(3): 60-63. HU Qinghui, ZHAO Zhengwen, LU Yujing. Studies and design of drilling fluid expert system[J]. Drilling Fluid & Completion Fluid, 2007, 24(3): 60-63. doi: 10.-3969/j.issn.1001-5620.2007.03.019 |
| [2] |
SHOKOUHI S V, SKALLE P, AAMODT A. An overview of case-based reasoning applications in drilling engineering[J]. Artificial Intelligence Review, 2014, 41(3): 317-329. doi: 10.1007/s10462-011-9310-2 |
| [3] |
王宝毅, 张宝生, 费沿光, 等. 基于案例推理的钻井复杂情况专家系统[J]. 石油大学学报(自然科学版), 2005, 29(6): 123-126. WANG Baoyi, ZHANG Baosheng, FEI Yanguang, et al. A drilling troubles expert system based on case-based reasoning[J]. Journal of the University of Petroleum, China, 2005, 29(6): 123-126. doi: 10.3321/j.issn:1000-5870.-2005.06.029 |
| [4] |
安丽娜, 张士杰. 专家系统研究现状及展望[J]. 计算机应用研究, 2007, 24(12): 1-5,19. AN Lina, ZHANG Shijie. Progress and prospects of expert system[J]. Application Research of Computers, 2007, 24(12): 1-5,19. doi: 10.3969/j.issn.1001-3695.2007.-12.001 |
| [5] |
袁勇, 董书杰, 刘文梅. 基于实例推理的钻井液配方设计系统[J]. 钻井液与完井液, 2005, 22(1): 31-34. YUAN Yong, DONG Shujie, LIU Wenmei. Case based reasoning designing system for drilling fluid formulation[J]. Drilling Fluid & Completion Fluld, 2005, 22(1): 31-34. doi: 10.3969/j.issn.1001-5620.2005.01.010 |
| [6] |
PLA A, LÓPEZ B, GAY P, et al. eXiT*CBR.v2:Distributed case-based reasoning tool for medical prognosis[J]. Decision Support Systems, 2013, 54(3): 1499-1510. doi: 10.1016/j.dss.2012.12.033 |
| [7] |
YAN Aijun, WANG Weixian, ZHANG Chunxiao, et al. A fault prediction method that uses improved case-based reasoning to continuously predict the status of a shaft furnace[J]. Information Sciences, 2014, 259(20): 269-281. doi: 10.1016/j.ins.2013.04.025 |
| [8] |
顾东晓, 李兴国, 梁昌勇, 等. 案例检索及权重优化方法研究及应用[J]. 系统工程学报, 2009, 24(6): 764-768. GU Dongxiao, LI Xingguo, LIANG Changyong, et al. Research on case retrieval with weight optimizing and its application[J]. Journal of Systems Engineering, 2009, 24(6): 764-768. doi: 10.3969/j.issn.1000-5781.2009.-06.020 |
| [9] |
PARK C S, HAN I. A case-based reasoning with the feature weights derived by analytic hierarchy process for bankruptcy prediction[J]. Expert Systems with Applications, 2002, 23(3): 255-264. doi: 10.1016/S0957-4174(02)00045-3 |
| [10] |
JI Aimin, ZHU Kun, HUANG Quansheng. Methods determining the weights of characteristics in mechanical products design on case-base reasoning[J]. Applied Mechanics & Materials, 2011, 138-139: 315-320. doi: 10.-4028/www.scientific.net/AMM.138-139.315
|
| [11] |
吴登生, 李建平, 孙晓蕾. 基于加权案例推理模型族的软件成本SVR组合估算[J]. 管理工程学报, 2015, 29(2): 210-216. WU Dengsheng, LI Jianping, SUN Xiaolei. Combination estimation of software effort by support vector regression based on multiple case-based reasoning with optimized weight[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(2): 210-216. doi: 10.13587/j.-cnki.jieem.2015.02.023 |
| [12] |
YAN Aijun, SHAO Hongshan, GUO Zhen. Weight optimization for case-based reasoning using membrane computing[J]. Information Sciences, 2014, 287: 109-120. doi: 10.1016/j.ins.2014.07.043 |
| [13] |
付雅芳, 刘晓东, 李延杰, 等. 基于遗传算法和案例推理的软件费用估算方法[J]. 计算机工程与应用, 2012, 48(8): 86-91. FU Yafang, LIU Xiaodong, LI Yanjie, et al. Software cost estimation method based on genetic algorithm and casebased reasoning[J]. Computer Engineering and Applications, 2012, 48(8): 86-91. doi: 10.3778/j.issn.1002-8331.-2012.08.024 |
| [14] |
王丽敏, 乔玲玲, 魏霖静. 结合遗传算法的优化卷积神经网络学习方法[J]. 计算机工程与设计, 2017, 38(7): 1945-1950. WANG Limin, QIAO Lingling, WEI Linjing. Optimal convolutional neural networks learning method combined with genetic algorithm[J]. Computer Engineering and Design, 2017, 38(7): 1945-1950. doi: 10.16208/j.issn1000-7024.2017.07.044 |
| [15] |
李海芳, 樊海亮, 金辉. 基于遗传算法的全局优化检索策略研究[J]. 计算机应用研究, 2009, 26(5): 1667-1669. LI Haifang, FAN Hailiang, JIN Hui. Strategy research of global optimization based on genetic algorithm[J]. Application Research of Computers, 2009, 26(5): 1667-1669. doi: 10.3969/j.issn.1001-3695.2009.05.018 |
| [16] |
孟庆宽, 张漫, 仇瑞承, 等. 基于改进遗传算法的农机具视觉导航线检测[J]. 农业机械学报, 2014, 45(10): 39-46. MENG Qingkuan, ZHANG Man, QIU Ruicheng, et al. Navigation line detection for farm machinery based on improved genetic algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 39-46. doi: 10.6041/j.issn.1000-1298.2014.10.007 |
| [17] |
万碧君, 罗健旭. 一种改进的基于案例推理的建模算法[J]. 华东理工大学学报(自然科学版), 2014, 40(5): 107-111. WAN Bijun, LUO Jianxu. An improved case-based reasoning modeling algorithm[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2014, 40(5): 107-111. doi: 10.3969/j.issn.1006-3080.2014.05.019 |
| [18] |
BAX E. Validation of nearest neighbor classifiers[J]. IEEE Transactions on Information Theory, 2004, 46(7): 2746-2752. doi: 10.1109/18.887892 |
| [19] |
边霞, 米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究, 2010, 27(7): 2425-2429,2434. BIAN Xia, MI Liang. Development genetic algorithm theory and its applications[J]. Application Research of Computers, 2010, 27(7): 2425-2429,2434. doi: 10.-3969/j.issn.1001-3695.2010.07.006 |
| [20] |
葛继科, 邱玉辉, 吴春明, 等. 遗传算法研究综述[J]. 计算机应用研究, 2008, 25(10): 2911-2916. GE Jike, QIU Yuhui, Wu Chunming, et al. Summary of genetic algorithms research[J]. Application Research of Computers, 2008, 25(10): 2911-2916. doi: 10.3969/j.-issn.1001-3695.2008.10.008 |
| [21] |
徐岩, 郅静. 基于改进自适应遗传算法的PMU优化配置[J]. 电力系统保护与控制, 2015, 43(2): 55-62. XU Yan, ZHI Jing. Optimal PMU configuration based on improved adaptive genetic algorithm[J]. Power System Protection and Control, 2015, 43(2): 55-62. |
| [22] |
陈乐亮. 我国钻井液体系分类的探讨[J]. 天然气工业, 1991, 11(4): 64-68. CHEN Leliang. A discussion on the classification of drilling fluid system in our country[J]. Natural Gas Industry, 1991, 11(4): 64-68. |
 2019, Vol. 41
2019, Vol. 41


