2. 中国石油北京油气调控中心, 北京 东城 100007;
3. 中国石油西南管道公司成都分控中心, 四川 成都 610213
2. Beijing Oil and Gas Pipeline Control Center, PetroChina, Dongcheng, Beijing 100007, China;
3. Southwest Pipeline Company, PetroChina, Chengdu, Sichuan 610213, China
大落差管道的排水放空过程,在放空点及出口背压的作用下,在泄流开始的瞬间形成“气顶液”两相流动。由于可变形的界面、可压缩的气相以及管流的三维性,气液两相流动成为两相流动中最为复杂的一种。在管路运行的实际情况中,管道中不同位置的参数难以达到稳定值。然而,对于某些管道,工艺参数的变化很小,尤其是在稳定状态下运行[1-2],属于慢瞬态流动。因此,用稳态模型近似描述管道的正常情况,计算工艺参数的分布情况也是可以接受的。1995年,Taitel以气液流动中气体处于准稳态的假设为基础,建立了一种以动态液相连续性方程为特征的四方程模型[3],并建立了稳态方程的3种模型。该简化模型可以应用于各种流型,得到稳定的数值解,但不能处理复杂的流动问题,其结果不够准确。
要准确模拟管流变化情况,应该采用瞬态流动模型进行分析。由于气液两相流动的三维特性以及长距离管流中的大流量,采用基于Navier-Stokes方程组的三维模型来研究瞬态两相流动是不切实际的[4]。因此,一维两相流模型在过去的几十年被广泛应用。目前应用最广的当属双流体模型,该模型分别对气液相建立连续性方程、动量方程和能量方程等6个方程,且考虑气液相间的摩擦阻力以及动量传递对流动过程的影响,所以双流体模型可以反映气液两相流动中两相流体之间的细微特征,非常适合描述相间自由表面运动剧烈和相间表面迁移捕捉等问题[5-9]。
如果按照模型中所含的方程数目来对近年来所得到的各种双流体模型进行分类,那么最简单的双流体模型当属Masella等研究中所用到的均压双流体模型,在这个模型中只采用气相和液相的连续性方程和动量方程,共4个平衡方程,且忽略参数在截面上分布的不均匀性,即截面上各点压力相等[10-13]。对于没有明显相态曲率效应的流型来说,四方程双流体模型是足够的。但当曲率效应显著,管流横截面积上相态间的压力差便不能再忽略不计,这时均压双流体模型不再适用[14]。2005年,Loilier在此基础上考虑了气体体积分数的变化、各组分温度之间的较小差别以及能量交换等因素,在4个平衡方程的基础上添加了气液混合物能量方程[15]。Ishii等研究中则给出了更加完整的双流体模型,分别列出气液两相的连续性方程、动量方程和能量方程等共6个平衡方程[16-17]。1999年,Saurel等在六方程双流体模型的基础上,加入了气体体积分数平衡方程,提出了一个包含了7个平衡方程的更为复杂的双流体模型[18]。2007年,Saurel等为这个七方程模型研究出了基于HLLC汇编语言的黎曼求解器,可用于计算各种流型的阻抗、相态界面处的流速以及压力[19]。除此之外,甚至还有更复杂的七方程双压双流体模型[20-22]。
虽然均压双流体模型是所有双流体模型中最简单的一种,但模型中的方程形式将随流动状态的发展而变化,且油气输送管道的瞬态响应相对较慢,所以并非模型越复杂越好,而是要根据具体物理条件进行选择[14, 23-27]。由Masella在1998年的模型对比实验研究可知[10],利用均压双流体模型模拟油气输送管道中的气液两相管流,不仅计算速度迅速,模拟结果与实验数据相比也非常准确,由于当油气输送管道在正常工况下运行时,系统的瞬态响应较其他输送管道相对较慢,因此,均压双流体模型可以很好地模拟油气输送管道中的两相流动。
处于多起伏、大落差地形的长距离输油管道,投产过程中出现的异常工况复杂多样,根据不同的工程实际,其造成因素及解决办法均有所不同,故国内虽有以解决投产过程出现的问题为目的的研究,却不能解决所有的异常工况。
处于多起伏、大高差地段的某原油管线含大落差“U”型管段,最大相对高差达1 432.64 m。在采用先注水后原油顶水的投产过程中,由于原油与水的密度差,“U”型管段左侧油压小于右侧液压,油头行进过程停滞,如图 1所示,这不仅严重影响投产进度和管道安全,还将导致混油量和末站污水处理量有较大的增加。
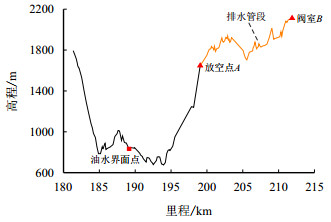 |
| 图1 某段大落差埋地原油管道 Fig. 1 Nujiang crossing pipes |
为解决这一问题,提出利用位于油水界面点右侧的阀室的压力泄放阀排水卸压的解决办法:放空点
 |
|
图2
排水管段 |
该管段起伏不断,在低洼处必有积水剩余,如图 3所示。
 |
| 图3 多起伏管段排水后仍有积液 Fig. 3 Water remained in the hilly pipeline |
当排空进入稳定状态(不再有流体从出口流出),管中仍有积液,而要确保排水后油压大于液柱压力,应尽可能多地排出管内液体,因此,利用OLGA多相流瞬态模拟方法对大落差管段的排水过程进行稳态、瞬态运行状况模拟,通过改变泄流孔径得到不同的模拟结果及可选泄流孔径,由模拟结果可得到选定管段(容量约为6 376.98 m
通过选取微元体,假设管道中的两相流在计算单元中为一维等温流动,在管道截面上的微观性质和压力分布不均匀可以忽略不计,即压力为均匀分布,忽略相间和相壁间的界面张力及湍流波动引起的应力。基于以上假设,通过应用气体、液体及液滴单独的连续性方程、界面传质、两个动量方程和一个混合能量守恒方程建立起一个均压六方程双流体模型。
(1) 质量守恒方程
气相
| $ \dfrac{\partial }{\partial t}\left( {{\beta }_{{\rm g}}}{{\rho }_{{\rm g}}} \right)=-\dfrac{1}{A}\dfrac{\partial }{\partial x}\left( A{{\beta }_{{\rm g}}}{{\rho }_{{\rm g}}}{{u}_{{\rm g}}} \right)+{{\varPsi }_{{\rm g}}}+{{q}_{{\rm g}}} $ | (1) |
壁面处液相
| $ \dfrac{\partial }{\partial t}\left( {{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}} \right)=-\dfrac{1}{A}\dfrac{\partial }{\partial x}\left( A{{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}}{{u}_{{\rm l}}} \right)-{{\varPsi }_{{\rm g}}}\dfrac{{{\beta }_{{\rm l}}}}{{{\beta }_{{\rm l}}}+{{\beta }_{{\rm d}}}}-\\{\kern 40pt}{{\varPsi }_{{\rm e}}}+{{\varPsi }_{{\rm d}}}+{{q}_{{\rm l}}} $ | (2) |
液滴
| $ \dfrac{\partial }{\partial t}\left( {{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}} \right)=-\dfrac{1}{A}\dfrac{\partial }{\partial x}\left( A{{\beta }_{{\rm d}}}{{\rho }_{{\rm l}}}{{u}_{{\rm d}}} \right)-{{\varPsi }_{{\rm g}}}\dfrac{{{\beta }_{\rm d}}}{{{\beta }_{{\rm l}}}+{{\beta }_{{\rm d}}}}-\\ {\kern 40pt} {{\varPsi }_{{\rm e}}}+{{\varPsi }_{{\rm d}}}+{{q}_{{\rm d}}}{\rm } $ | (3) |
式中:
(2) 动量方程
气相+液滴的动量方程
| $ \dfrac{\partial }{\partial t}\left( {{\beta }_{{\rm g}}}{{\rho }_{{\rm g}}}{{u}_{{\rm g}}}+{{\beta }_{{\rm d}}}{{\rho }_{{\rm l}}}{{u}_{{\rm d}}} \right)=-\left( {{\beta }_{{\rm g}}}+{{\beta }_{{\rm d}}} \right)\dfrac{\partial p}{\partial x}- %\\[6pt]{\kern 40pt} \dfrac{1}{A}\dfrac{\partial }{\partial x}\left( A{{\beta }_{{\rm g}}}{{\rho }_{{\rm g}}}u_{{\rm g}}^{2}+A{{\beta }_{{\rm d}}}{{\rho }_{{\rm l}}}u_{{\rm d}}^{2} \right)-\\{\kern 40pt} \dfrac{1}{2}{{\lambda }_{{\rm g}}}{{\rho }_{{\rm g}}}{{u}_{{\rm g}}}\left| {{u}_{{\rm g}}} \right|\dfrac{{{S}_{{\rm g}}}}{4A} -\dfrac{1}{2}{{\lambda }_{{\rm i}}}{{\rho }_{{\rm g}}}{{u}_{{\rm r}}}\left| {{u}_{{\rm r}}} \right|\dfrac{{{S}_{{\rm i}}}}{4A}- %\\{\kern 40pt} \left( {{\beta }_{{\rm g}}}{{\rho }_{{\rm g}}}+{{\beta }_{{\rm d}}}{{\rho }_{{\rm l}}} \right){\rm g}\sin {\rm }\theta{\rm }+\\ {{\varPsi }_{{\rm g}}}\dfrac{{{\beta }_{{\rm l}}}}{{{\beta }_{{\rm l}}}+{{\beta }_{{\rm d}}}}{{u}_{{\rm a}}}+ %\\{\kern 40pt} {{\varPsi }_{{\rm e}}}{{u}_{{\rm i}}}-{{\varPsi }_{{\rm d}}}{{u}_{{\rm d}}} $ | (4) |
式中:
相对速度满足滑移方程
| $ {{u}_{{\rm g}}}={{R}_{{\rm D}}}\left( {{u}_{{\rm l}}}+{{u}_{{\rm r}}} \right) $ | (5) |
式中:
液相动量方程
| $ \dfrac{\partial }{\partial t}\left( {{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}}{{u}_{{\rm l}}} \right)=-{{\beta }_{{\rm l}}}\dfrac{\partial p}{\partial x}-\\ \dfrac{1}{A}\dfrac{\partial }{\partial x}\left( A{{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}}u_{{\rm l}}^{2} \right)-%\\[6pt]{\kern 40pt} \dfrac{1}{2}{{\lambda }_{{\rm l}}}{{\rho }_{{\rm l}}}{{u}_{{\rm l}}}\left| {{u}_{{\rm l}}} \right|\dfrac{{{{S}}_{{\rm l}}}}{4A}+{{\lambda }_{{\rm i}}}\dfrac{1}{2}{{\rho }_{{\rm g}}}{{u}_{{\rm r}}}\left| {{u}_{{\rm r}}} \right|\dfrac{{{{S}}_{{\rm i}}}}{4A}- \\{\kern 40pt} {{\beta }_{{\rm l}}}{{\rho }_{{\rm l}}}{\rm g}\sin \theta +{{\varPsi }_{{\rm g}}}\dfrac{{{\beta }_{{\rm l}}}}{{{\beta }_{{\rm l}}}+{{\beta }_{{\rm d}}}}{{u}_{{\rm a}}}-{{\varPsi }_{{\rm e}}}{{u}_{{\rm i}}}+%\\{\kern 40pt} {{\varPsi }_{{\rm d}}}{{u}_{{\rm d}}}-\\ {{\beta }_{{\rm l}}}D\left( {{\rho }_{{\rm l}}}-\rho_{\rm g} \right){\rm g}\dfrac{\partial {{\beta }_{{\rm l}}}}{\partial x}\cos \theta $ | (6) |
式中:
液滴速率
| $ {{u}_{{\rm d}}}={{u}_{{\rm g}}}-{{u}_{{\rm 0D}}}\sin \theta $ | (7) |
式中:
(3) 能量方程
假设气液具有相同的温度,并且单元控制体内的温度相同,这里只采用气液混合能量方程
| $ \dfrac{\partial }{\partial t}\left[ {{\rho }_{{\rm g}}}A{{\phi }_{{\rm g}}}{\rm d}x\left( {{E}_{{\rm g}}}+\dfrac{1}{2}u_{{\rm g}}^{2}+{\rm g}h \right)+\\ {{\rho }_{{\rm l}}}A{{\phi }_{{\rm l}}}{\rm d}x\left( {{E}_{{\rm l}}}+\dfrac{1}{2}u_{{\rm l}}^{2}+{\rm g}h \right)+{{\rho }_{{\rm l}}}A{{\phi }_{{\rm d}}}{\rm d}x\left( {{E}_{{\rm d}}}+\dfrac{1}{2}u_{{\rm d}}^{2}+{\rm g}h \right) \right]{\rm d}t= \\{\kern 40pt} -\dfrac{\partial }{\partial x}\left[ {{G}_{{\rm g}}}{{\phi }_{{\rm g}}}{\rm d}t\left( {{h}_{{\rm g}}}+\dfrac{1}{2}u_{{\rm g}}^{2}+{\rm g}h \right)+\\ {{G}_{{\rm d}}}{{\phi }_{{\rm d}}}{\rm d}t\left( {{h}_{{\rm d}}}+\dfrac{1}{2}u_{{\rm d}}^{2}+{\rm g}h \right)+{{G}_{{\rm l}}}{{\phi }_{{\rm l}}}{\rm d}t\left( {{h}_{{\rm l}}}+\dfrac{1}{2}u_{{\rm l}}^{2}+{\rm g}h \right) \right]{\rm d}x+H_{\rm s}+U $ | (8) |
式中:
g——重力加速度,g = 9.8 m/s
在双流体(气液)模型的基础上,综合计算两相流参数并判断流型,然后由流型计算处各参数值,模型的基本方程采用欧拉法求解,在欧拉格式中还采用了拉格朗日的前缘跟踪格式。利用交错网格,通过有限体积法,将管线离散成许多控制体单元,其密度、压力和温度等变量存储在控制体的中心,而流速和流量等变量存储在控制体的边界上。
2 大落差管段排水过程仿真 2.1 物理模型以大型“U”型管段的右侧为排水过程的模拟管段,即图 1中的排水管段段,其地形概况见图 4。
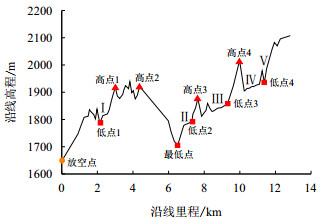 |
| 图4 排水管段地形概况 Fig. 4 Geography of the featured drainage section |
由图 4可以看出,该排水管段属于典型的大落差管道,全线有5处较大的起伏地段。
现场和模拟均采用
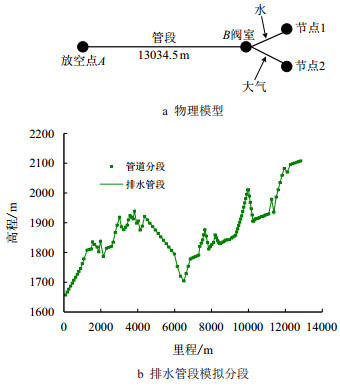 |
| 图5 排水管段模拟物理模型 Fig. 5 Physical model of the featured pipeline |
模拟管段设计压力15 MPa,壁厚17.5 mm,管径为813.0 mm,粗糙度为0.01 mm。
在实际排水过程中,里程0处的压力泄放阀室为唯一放空点,在物理模型中,里程12.831 km处设截止阀,防止流体倒流,其中,截止阀口径取800 mm,管道内径778 mm,流量系数0.84;起点质量流量为900 kg/h,起终点温度均为295 K,终点压力为0.1 MPa。
3 仿真结果分析 3.1 泄流孔径及排水量以泄流孔径为变量,为使管道得到完全放空,将不同泄流孔径下的模拟排水时间均设定为72 h。模拟计算后,得到一系列可选泄流孔径为30
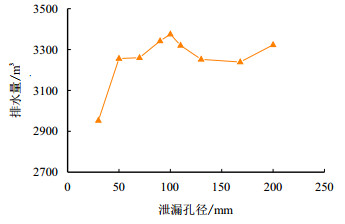 |
| 图6 排水量随泄流孔径变化曲线 Fig. 6 Leaking aperture-leakage relation curve |
由图 6可见,各泄流孔径对应的最大排水量虽然不尽相同,但相差不大。由于排水时间相同且管段总容量不变,因此,由图 6可直接反映不同泄流孔径下的排水率。泄流孔径越大,排水率越高:充满水的大落差起伏管段在排水过程中,将在低洼处形成积液,随着泄流孔径的增大,排水速度逐渐加快,低洼处积水的剩余动能随之增大,剩余动能越大,积水越容易从低洼处激荡出来,从而使得排水量有所增加,但积水量达到稳定的时间也随着排水速度的增大而增加,故在相同的排水时间中排水量有所不同。
图 7为放空点流量稳定时间随泄流孔径变化曲线。
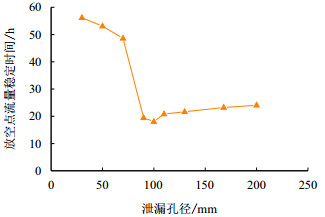 |
| 图7 放空点流量稳定时间随泄流孔径变化曲线 Fig. 7 Settling time of flow rate at the vent-leaking aperture relation curve |
随着泄流孔径的增加,放空点流量的稳定时间先减少后增加;其中,最小泄流孔径30 mm所对应的流量稳定时间最长,为56.16 h;当泄流孔径为100 mm时,放空点流量稳定时间最短,为18.05 h。在足够长的排水时间内,排水管段达到的最大排水量相差不大,泄流孔径为30
图 8为各泄流孔径得到相同排水量所需排水时间。泄流孔径越小,排水速率越慢,当泄流孔径为130 \mbox{mm}时,所需排水时间最短;当泄流孔径为30 mm时,时间最长,约为最短排水时间的10倍,排水过慢,本文不考虑此工况。由于工程实际不可能在输油管道上直接开孔,而是在泄压阀室的支管上,考虑到
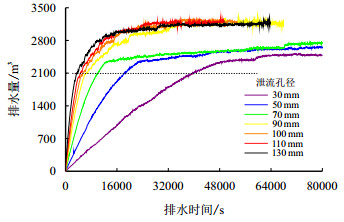 |
| 图8 排水量随时间变化曲线 Fig. 8 Leakage-time relation curves |
不同泄流孔径的管内持液量随时间变化曲线如图 9所示。
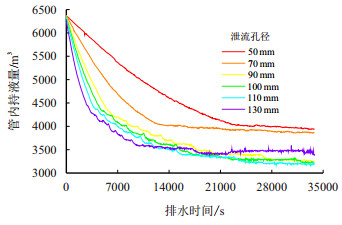 |
| 图9 管内持液量随排水时间变化曲线 Fig. 9 Liquid hold-up in pipeline-time relation curves |
由图 9可看出,持液量先是迅速减小后呈极慢的下降趋势,是因为随着泄流孔径的增加,排水速率加快,排水管道拉空得越快,越容易进入低洼积水激荡阶段(积水由于惯性荡出低洼处)。由于积水的剩余动能随着排水速率增大而增大,剩余动能越大,积水越容易由于惯性荡出低洼处,从而使得管内持液量减少,但由于本段管道落差较大,起伏剧烈,低洼处较多,从上游激荡出来的积水需要较长时间才能到达放空点,当排水放空进行到一定时间后,持液量在浮动中极缓慢地下降。
3.2 工程排水结束时间与放空点流量稳定时间 3.2.1 工程排水结束时间本文的目的是得到适用于工程实际的最佳泄流孔径及相应的排水时间,但对于工程实际而言的排水结束时间与理论上的完全放空结束时间不同,在实际工程中的排水过程不需要达到排水管段的完全放空阶段。如图 9所示,在经过快速下降后,排水管段的管内持液量是以极慢的速度下降的,显然管内持液量达到定值所需时间远超工程实际中进行一次泄压作业时间的合理范围,因此,工程排水时间不应取理论完全放空结束时间。基于此,本文提出在放空点设流量监测点,观察放空点的流量变化来判断排水过程的进展,工程排水结束时间即取放空点流量稳定时间。
3.2.2 放空点流量稳定时间由图 9可知,从泄流开始的瞬间到某时间点之后,持液量以极缓慢的速度减小,需要很长时间才能不再变化,因此,通过持液量的变化来判断实际排水放空的结束时间是不准确的。
作为排水过程的唯一放空点,该点的流量可直观地反映排水过程,当唯一放空点的流量约为0且较长时间内不再变化时,可停止排水。
各泄流孔径下放空点的流量随时间变化曲线如图 10所示。
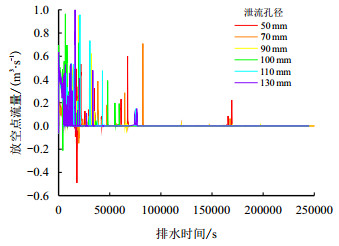 |
| 图10 放空点流量随时间变化曲线 Fig. 10 Flow rate at the vent-time relation curves |
随着泄流孔径的增大,放空点的流量波动范围明显增大;泄流开始时大量水流通过放空点排出,但随时间的增加管内持液量迅速减少,因此,放空点流量骤增,随后逐渐下降。但由于水流流过低洼后,积水剩余动能较大,将溢出一部分,因此,流量变化出现一定的脉动性。当放空过程进行到某个时间点,一直到模拟时间结束,流量都不再有任何波动,且数量级为1×10
由图 10可知,随着泄流孔径的增加,流量达到稳定所需时间先减少后增大,这是因为随着泄流孔径的增大,排水速度逐渐加快,低洼处积水的剩余动能随之增大,积水量达到稳定的时间也随之增加。
3.3 重点位置压力监测 3.3.1 管线最低点由于本管段所处地区地势起伏较大,相对高差达460.36 m,为避免在排水过程中出现水击及爆管,排水过程中的压力波动不能大于管道设计压力15.00 MPa,故在管线最低点处设压力监测点,最低点位置如图 4所示。
不同泄流孔径的最低点压力变化曲线如图 11所示,由图可以看出,最低点最大压力初始值为4.67 MPa,远小于设计压力15.00 MPa,在泄流开始的一瞬间,压力骤降,排水过程中管线最低点处的压力变化也逐渐趋于平稳。
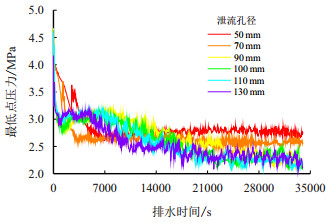 |
| 图11 最低点压力变化曲线 Fig. 11 Pressure at the bottom point variation curves |
选取管段中4个高点作为压力监测点,高点1
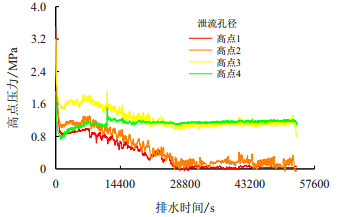 |
| 图12 各高点压力变化曲线 Fig. 12 Pressure at top elbow variation curves |
除了高点4外,其他高点的压力变化趋势均为在排水开始时,压力迅速下降,后逐渐减小,并围绕某数值微微上下浮动。高点4,在急剧下降之后压力有所回升并趋于平稳,然后保持不变。在高点1处的压力最小,在25 200 s后,高点1压力常常出现小于0的情况,即在排水过程中高点1将出现负压情况,此时高点1压力等于或小于水的饱和蒸汽压,使得少量水汽化,形成拉空。
鉴于高点1
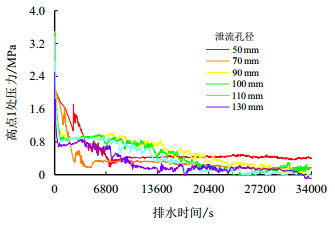 |
| 图13 高点1的压力变化曲线 Fig. 13 Pressure variation at top elbow 1 |
如图 13所示,当泄流孔径小于90 mm时,高点压力随时间响应较慢;当泄流孔径大于90 mm时,高点压力随时间的响应速度明显加快,且泄流孔径越大,压力波动越激烈,高点1压力越小,表明拉空越剧烈,然而剧烈的拉空容易造成弥合水击,对管道造成破坏,因此,在排水过程中泄流孔径不宜过大,以避免剧烈拉空带来的水击效应。
3.3.3 管线低点在模拟过程中,除了重点监测最低点及高点的压力变化外,还要特别注意具有较大起伏段后的低点,因为水流经过高点后流至具有较大起伏的低点,由于高差其动能有较大增加,对低点的冲击压力随之增大,为防止出现水击及爆管,选取管段中除最低点外4个低点作为压力监测点,低点1
由于各泄流孔径对应的最低点压力变化曲线总体变化趋势一致(图 11),因此,以泄流孔径为100 mm为例,各低点压力随时间变化曲线见图 14。
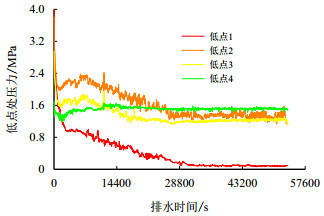 |
| 图14 各低点压力变化曲线 Fig. 14 Pressure variation curves at low elbows |
图 14中,各低点的整体压力变化趋势呈现出与高点的整体压力变化趋势相似的现象,并且在排水过程中各低点的压力变化在0.013 6
放空点压力在不同泄流孔径下的随时间的变化情况如图 15所示。由图 15可见,起点压力的总体变化趋势与泄流孔径无关,均为泄流开始的一瞬间骤降,随后在一段时间内下降到某值,之后便稳定在该值,只有细微的波动,波动随着泄流孔径的减小而逐渐缓和,而稳定压力值随着泄流孔径的增大而逐渐减小。不难看出,泄流孔径越大,压力下降得越快。
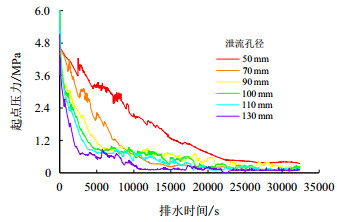 |
| 图15 起点压力随时间变化曲线 Fig. 15 Pressure at the vent-time relation curves |
(1) 大落差输油管道排水过程研究可以得到排水管段的最低点、高点、具有较大起伏的低点和起点等处的压力、流量随时间变化情况,便于了解全管线放空时管道运行参数的变化情况。
(2) 对于大落差管道的放空,适当增大泄流孔径可提高排水率和排水速率,但泄流孔径过大会造成管道高点剧烈拉空,形成弥合水击,破坏管道。
(3) 排水管段的起点、最低点、低点及高点的总体压力变化趋势,与泄流孔径无关,泄流孔径只影响其压力波动程度,泄流孔径越大,压力波动越剧烈。
(4) 当泄流孔径为90
| [1] |
EL-OUN Z. Gas-liquid two-phase flow in pipelines[C]. SPE 20645-MS, 1990. doi: 10.2118/20645-MS
|
| [2] |
GUO Liejin, LI Guangjun, CHEN Xuejun. A linear and non-linear analysis on interfacial instability of gas-liquid two-phase flow through a circular pipe[J]. International Journal of Heat & Mass Transfer, 2002, 45(7): 1525-1534. doi: 10.1016/S0017-9310(01)00247-2 |
| [3] |
TAITEL Y, BARNEA D, BRILL J P. Stratified three phase flow in pipes[J]. International Journal of Multiphase Flow, 1995, 21(1): 53-60. doi: 10.1016/0301-9322(94)00058-R |
| [4] |
SALHI Y, SI-AHMED E K, LEGRAND J, et al. Stability analysis of inclined stratified two-phase gas-liquid flow[J]. Nuclear Engineering & Design, 2010, 240(5): 1083-1096. doi: 10.1016/j.nucengdes.2009.12.027 |
| [5] |
赵铎.水平管内气液两相流流型数值模拟与实验研究[D].东营: 中国石油大学(华东), 2007. doi: 10.7666/-d.y1214163 ZHAO Duo. Numerical simulation and experiment research on flow pattern of gas-liquid flow in horizontal pipe[D]. Dongying: China University of Petroleum(East China), 2007. doi: 10.7666/d.y1214163 |
| [6] |
刘定智.多相混输技术的研究及其应用[D].成都: 西南石油学院, 2003. LIU Dingzhi. Research of multiphase mixture transportation techniques and its applications[D]. Chengdu: Southwest Petroleum Institute, 2003. |
| [7] |
KONG R, KIM S. Characterization of horizontal air-water two-phase flow[J]. Nuclear Engineering & Design, 2016, 312(6): 266-276. doi: 10.1016/j.nucengdes.2016.06.016 |
| [8] |
GUO B, SONG S, CHACKO J, et al. Gas-liquid multiphase flow in pipeline-Offshore pipelines[M]. 2014. doi: 10.1016/B978-075067847-6/50074-3
|
| [9] |
MANABE R, TOCHIKAWA T, TSUKUDA M, et al. Experimental and modeling studies of two-phase flow in pipelines[J]. SPE 37017-PA, 1997. doi: 10.2118/37017-PA |
| [10] |
MASELLA J M, TRAN Q H, FERRE D, et al. Transient simulation of two-phase flows in pipes[J]. International Journal of Multiphase Flow, 1998, 24(5): 739-755. doi: 10.1016/S0301-9322(98)00004-4 |
| [11] |
ISSA R I, KEMPF M H W. Simulation of slug flow in horizontal and nearly horizontal pipes with the two-fluid model[J]. International Journal of Multiphase Flow, 2003, 29(1): 69-95. doi: 10.1016/S0301-9322(02)00127-1 |
| [12] |
BONIZZI M, ISSA R I. A model for simulating gas bubble entrainment in two-phase horizontal slug flow[J]. International Journal of Multiphase Flow, 2003, 29(11): 1685-1717. doi: 10.1016/j.ijmultiphaseflow.2003.09.001 |
| [13] |
OMGBA-ESSAMA C. Numerical modelling of transient gas-liquid flows(Application to stratified and slug flow regimes)[D]. Bedfordshire: Cranfield University, 2004.
|
| [14] |
FIGUEIREDO A B, BAPTISTA R M, RACHID F B D F, et al. Numerical simulation of stratified-pattern two-phase flow in gas pipelines using a two-fluid model[J]. International Journal of Multiphase Flow, 2017, 88: 30-49. doi: 10.1016/j.ijmultiphaseflow.2016.09.016 |
| [15] |
LOILIER P, OMGBA-ESSAMA C, THOMPSON C. Numerical experiments of two-phase flow in pipelines with a two-fluid compressible model[C]//12th International Conference in Multiphase Production Technology, Barcelona, Spain, 2005.
|
| [16] |
ISHⅡ M, MISHIMA K. Two-fluid model and hydrodynamic constitutive relations[J]. Nuclear Engineering & Design, 1984, 82(2): 107-126. doi: 10.1016/0029-5493(84)90207-3 |
| [17] |
SIMÕES E F, CARNEIRO J N E, NIECKELE A O. Numerical prediction of non-boiling heat transfer in horizontal stratified and slug flow by the two-fluid model[J]. International Journal of Heat & Fluid Flow, 2014, 47: 135-145. doi: 10.1016/j.ijheatfluidflow.2014.03.005 |
| [18] |
SAUREL R, ABGRALL R. A multiphase Godunov method for compressible multi-fluid and multiphase flows[J]. Journal of Computational Physics, 1999, 150(2): 425-467. doi: 10.1006/jcph.1999.6187 |
| [19] |
SAUREL R, MéTAYER O L, MASSONI J, et al. Shock jump relations for multiphase mixtures with stiff mechanical relaxation[J]. Shock Waves, 2007, 16(3): 209-232. doi: 10.1007/s00193-006-0065-7 |
| [20] |
EMONOT P, SOUYRI A, GANDRILLE J L, et al. A new system code for thermal-hydraulics in the context of the NEPTUNE project[J]. Nuclear Engineering & Design, 2011, 241(11): 4476-4481. doi: 10.1016/j.nucengdes.-2011.04.049 |
| [21] |
FEI C, SHAN J, PAN W U, et al. Analysis of virtual mass force and interfacial pressure on the well-posedness of the two-fluid six-equation model[C]//8th International Symposium on Symbiotic Nuclear Power Systems for 21st Century, 2016.
|
| [22] |
FURFARO D, SAUREL R. A simple HLLC-type Riemann solver for compressible non-equilibrium two-phase flows[J]. Computers & Fluids, 2015, 111: 159-178. doi: 10.1016/j.compfluid.2015.01.016 |
| [23] |
HUANG Shanfang, ZHANG Bingdong, LU Jun, et al. Study on flow pattern maps in hilly-terrain air-water-oil threephase flows[J]. Experimental Thermal & Fluid Science, 2013, 47(5): 158-171. doi: 10.1016/j.expthermflusci.-2013.01.011 |
| [24] |
KUSHNIR R, SEGAL V, ULLMANN A, et al. Closure relations effects on the prediction of the stratified twophase flow stability via the two-fluid model[J]. International Journal of Multiphase Flow, 2017, 97: 78-93. doi: 10.1016/j.ijmultiphaseflow.2017.07.010 |
| [25] |
LEE S J, LEE J H, KIM B J. Improvement of the two-fluid momentum equation using a modified Reynolds Stress model for horizontal turbulent bubbly flows[J]. Chemical Engineering Science, 2017, 173: 208-217. doi: 10.1016/-j.ces.2017.07.038 |
| [26] |
LIU Xianfei, ZHAO Donghai, LIU Yifeng, et al. Numerical analysis of the two-phase flow characteristics in vertical downward helical pipe[J]. International Journal of Heat & Mass Transfer, 2017, 108: 1947-1959. doi: 10.-1016/j.ijheatmasstransfer.2017.01.056 |
| [27] |
Schlumberger. Dynamic multiphase flow simulator[R]. Schlumberger User's Manual, 2015.
|
 2019, Vol. 41
2019, Vol. 41


