油井出砂是渤海油田疏松砂岩储层生产过程中面临的最普遍问题之一[1-4],危害十分严重,比如磨蚀地面及井下设备、损害储层、降低产能、堵塞井眼、污染环境等,甚至导致油井停产或报废[5-6]。目前,出砂已成为渤海油田低产低效井和长停井的主要成因之一,井数多达150余口,主要分布在绥中、蓬莱和南堡等油田。出砂风险的准确预测是合理优化防砂措施的关键所在,尤其是储层开发全生命周期内的动态出砂情况的预测对油井长效防砂尤为重要[7-9]。渤海油田出砂预测主要采用测井法、实验法和现场观测法等[10-13],均为基于静态资料分析的静态预测法,难以实现生产过程中的动态出砂风险预测,对防砂方式的设计指导偏笼统[14-15]。此外,部分学者对动态出砂预测方法进行了探索,如在静态模型采用动态压力亏空因子和含水率因子修正,考虑含水率变化对岩石强度的影响,或将配产压差和岩石强度作逐年对比等[7-9],但现有研究相对偏简单,同时,这些动态预测方法尚未应用到渤海油田。因此,亟需结合渤海油田油井类型、完井方式等特征,建立适用于渤海油田的多因素全生命周期动态出砂预测方法,进一步优化完井方式,降本增效。
1 储层动态出砂影响因素及机理影响储层出砂的因素众多,包括原地应力状态、孔隙压力、流体性质、生产压差、含水率、完井方式、射孔参数、压力亏空等,具体可分为地质因素、开采因素和工程因素3大类[16]。这些因素相互影响,使得出砂问题十分复杂,仅凭经验难以确定各影响因素的主次,因此,建立多因素综合出砂预测方法更有意义。研究表明,地应力、含水率、生产压差、压力亏空等是影响储层动态出砂的关键因素[12-14, 17-20]。
(1) 含水率变化的影响
对于一些大型边、底水油藏,随着生产不断进行,含水率会不断上升,岩石泡水后,岩石中的亲水矿物(如黏土矿物)水化膨胀,从而影响岩石强度。研究表明[13, 18-21],生产过程中岩石强度主要受含水率和矿物亲水性影响,含水率越高,岩石强度降幅越大;岩石中亲水矿物含量越多,泡水后的岩石强度影响越大。岩石中亲水矿物含量最多的是黏土矿物,其在浸湿后强度降低至70%。
(2) 生产压差的影响
生产压差对出砂的影响主要体现在生产过程中会产生一个径向摩擦拖曳力,该附加应力会将岩石表面颗粒向井眼内拖曳,使近井地带岩石发生拉伸破坏[11-12, 19, 21]。该拖曳力主要由生产压差产生,属于拉应力,使岩石表面颗粒朝着流体流动方向运动,因此,生产压差越大,流体摩擦拖曳力越大,出砂风险也越高。
(3) 储层压力亏空的影响
随着储层油气的不断采出,储层压力会不断衰竭亏空,相当于岩石所处的外部环境在不断地变化,受力不断变化。研究表明,储层压力亏空(衰竭)不但直接影响储层多孔介质孔隙流体压力,还影响地层有效主应力[13]。一般而言,压力亏空使井壁岩石切向有效应力增加,降低了井眼的稳定能力,当剪切应力超过岩石的抗剪强度时导致岩石崩落破碎[17]。
2 疏松砂岩储层动态出砂预测模型渤海油田疏松砂岩储层目前主要采用定向井和水平井两种井型开采,其中定向井的完井方式主要为套管射孔完井,水平井的主要完井方式为裸眼完井。因此,分定向套管井和水平裸眼井两类为对象,分别建立疏松砂岩储层动态出砂预测模型。
2.1 定向套管井预测模型 2.1.1 射孔孔壁周向应力分布根据线—弹性力学理论,Fairhurst推导得到直井井周应力分布为[22]
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{{\rm{re}}}} = \frac{{{\sigma _{{\rm{H1}}}} + {\sigma _{{\rm{H2}}}}}}{2}\left( {1 - \frac{{r_{\rm{w}}^2}}{{{r^2}}}} \right) + \frac{{{\sigma _{{\rm{H1}}}} - {\sigma _{{\rm{H2}}}}}}{2}\left( {1 + \frac{{3r_{\rm{w}}^4}}{{{r^4}}} - \frac{{4r_{\rm{w}}^2}}{{{r^2}}}} \right)\cos 2\theta + {p_{{\rm{wf}}}}\left( t \right)\frac{{r_{\rm{w}}^2}}{{{r^2}}} - {p_{\rm{p}}}\left( t \right)}\\ {{\sigma _{{\rm{ \mathsf{ θ} e}}}} = \frac{{{\sigma _{{\rm{H1}}}} + {\sigma _{{\rm{H2}}}}}}{2}\left( {1 + \frac{{r_{\rm{w}}^2}}{{{r^2}}}} \right) - \frac{{{\sigma _{{\rm{H1}}}} - {\sigma _{{\rm{H2}}}}}}{2}\left( {1 + \frac{{3r_{\rm{w}}^4}}{{{r^4}}}} \right)\cos 2\theta - {p_{{\rm{wf}}}}\left( t \right)\frac{{r_{\rm{w}}^2}}{{{r^2}}} - {p_{\rm{p}}}\left( t \right)}\\ {{\sigma _{{\rm{ze}}}} = {\sigma _{\rm{v}}} - 2\mu \left( {{\sigma _{{\rm{H1}}}} - {\sigma _{{\rm{H2}}}}} \right)\frac{{r_{\rm{w}}^2}}{{{r^2}}}\cos 2\theta - {p_{\rm{p}}}\left( t \right)} \end{array}} \right. $ | (1) |
式中:
为了简化分析,将射孔孔道假设为细长型(图 1),得到射孔孔壁应力分布见式(2)。
| $ \left\{ \begin{array}{l} {{\sigma }_{{\rm se}}}=\frac{{{\sigma }_{{\rm{ \mathsf{ θ} e}}}}+{{\sigma }_{\rm ze}}}{2}\left( 1-\frac{r_{\rm p}^{2}}{{{s}^{2}}} \right)+\frac{{{\sigma }_{{\rm{ \mathsf{ θ} e}}}}-{{\sigma }_{\rm ze}}}{2}\left( 1+\frac{3r_{\rm p}^{4}}{{{s}^{4}}}-\frac{4r_{\rm p}^{2}}{{{s}^{2}}} \right)\cos~2\psi +\frac{r_{\rm p}^{2}}{{{s}^{2}}}{{p}_{\rm pf}}\left( t \right) \\ {{\sigma }_{{\rm{\Psi }} {\rm e}}}=\frac{{{\sigma }_{{\rm{ \mathsf{ θ} e}}}}+{{\sigma }_{\rm ze}}}{2}\left( 1+\frac{r_{\rm p}^{2}}{{{s}^{2}}} \right)-\frac{{{\sigma }_{{\rm{ \mathsf{ θ} e}}}}-{{\sigma }_{\rm ze}}}{2}\left( 1+\frac{3r_{\rm p}^{4}}{{{s}^{4}}} \right)\cos~2\psi -\frac{r_{\rm p}^{2}}{{{s}^{2}}}{{p}_{\rm pf}}\left( t \right) \\ \end{array} \right. $ | (2) |
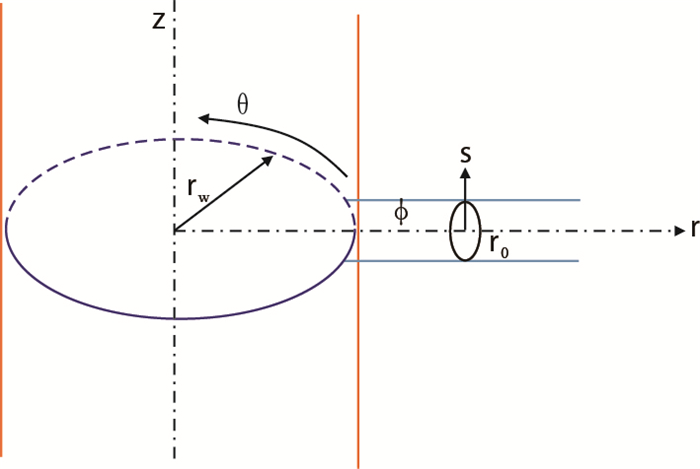 |
| 图1 射孔孔眼坐标系与井眼坐标系的相对关系 Fig. 1 The relative relations of coordinate system between perforation tunnel and hole |
式中:
令
| $ \left\{ \begin{array}{l} {{\sigma }_{{\rm se}}}={{p}_{\rm pf}}\left( t \right) \\ {{\sigma }_{{\rm{\Psi }} {\rm e}}}={{\sigma }_{{\rm{ \mathsf{ θ} e}}}}+{{\sigma }_{\rm ze}}-\\ {\kern 40pt}2({{\sigma }_{{\rm{ \mathsf{ θ} e}}}}- {{\sigma }_{\rm ze}})\cos~2\psi -{{p}_{\rm pf}}\left( t \right) \end{array} \right. $ | (3) |
式中:
在直井模型基础上,用式(4)对原地应力进行转换,将变换后的原地应力分量代入直井射孔孔壁周向应力分布模型,得定向井射孔孔壁应力分布,见式(5)。
| $ \left\{ \begin{array}{l} {{\sigma }_{x}}={{\cos }^{2}}\alpha \left( {{\sigma }_{\rm H1}}{{\cos }^{2}}\beta +{{\sigma }_{\rm H2}}{{\sin }^{2}}\beta \right)+{{\sigma }_{\rm v}}{{\sin }^{2}}\beta \\ {{\sigma }_{y}}={{\sigma }_{\rm H1}}{{\sin }^{2}}\beta +{{\sigma }_{\rm H2}}{{\cos }^{2}}\beta \\ {{\sigma }_{z}}={{\sin }^{2}}\alpha \left( {{\sigma }_{\rm H1}}{{\cos }^{2}}\beta +{{\sigma }_{\rm H2}}{{\sin }^{2}}\beta \right)+{{\sigma }_{\rm v}}{{\cos }^{2}}\alpha \\ {{\tau }_{xy}}=\cos \alpha \sin \beta \cos \beta \left( {{\sigma }_{\rm H1}}-{{\sigma }_{\rm H2}} \right) \\ {{\tau }_{xz}}=\cos \alpha \sin \alpha \left( {{\sigma }_{\rm H1}}{{\cos }^{2}}\beta +{{\sigma }_{\rm H2}}{{\sin }^{2}}\beta -{{\sigma }_{\rm v}} \right) \\ {{\tau }_{yz}}=\sin \alpha \sin \beta \cos \beta \left( {{\sigma }_{\rm H1}}-{{\sigma }_{\rm H2}} \right) \\ \end{array} \right. $ | (4) |
式中:
| $ \left\{ \begin{array}{l} {{\sigma }_{\rm re}}\!=\!\frac{{{\sigma }_{x}}\!+\!{{\sigma }_{y}}}{2}\left (1\!-\!\frac{r_{\rm w}^{2}}{{{r}^{2}}}\right )\!+\!\frac{{{\sigma }_{x}}\!-\!{{\sigma }_{y}}}{2}\left (1\!+\!\frac{3r_{\rm w}^{4}}{{{r}^{4}}}\!-\!\frac{4r_{\rm w}^{2}}{{{r}^{2}}}\right )\cos~2\theta \!+\!{{\tau }_{xy}}\left ( 1\!+\!\frac{3r_{\rm w}^{4}}{{{r}^{4}}}\!-\!\frac{4r_{\rm w}^{2}}{{{r}^{2}}} \right){\sin}~2\theta +\!{{p}_{\rm wf}}\left ( t \right)\frac{r_{\rm w}^{2}}{{{r}^{2}}}\!-\!{{p}_{\rm p}}\left( t \right) \\ {{\sigma }_{\theta \rm e}}\!=\!\frac{{{\sigma }_{x}}+{{\sigma }_{y}}}{2}\left (1+\frac{r_{\rm w}^{2}}{{{r}^{2}}}\right )-\frac{{{\sigma }_{x}}-{{\sigma }_{y}}}{2}\left (1+\frac{3r_{\rm w}^{4}}{{{r}^{4}}}\right )\cos 2\theta -{{\tau }_{xy}}\left( 1+\frac{3r_{\rm w}^{4}}{{{r}^{4}}} \right)\sin~2\theta -{{p}_{\rm wf}}\left( t \right)\frac{r_{\rm w}^{2}}{{{r}^{2}}}-{{p}_{\rm p}}\left( t \right) \\ {{\sigma }_{\rm ze}}\!=\!{{\sigma }_{z}}-2\mu \left ({{\sigma }_{x}}-{{\sigma }_{y}}\right )\frac{r_{\rm w}^{2}}{{{r}^{2}}}\cos~2\theta -4\mu {{\tau }_{xy}}\frac{r_{\rm w}^{2}}{{{r}^{2}}}\sin~2\theta -{{p}_{\rm p}}\left( t \right) \\ \end{array} \right. $ | (5) |
流体摩擦拖曳力主要由生产压差引起,若在单位渗流面积上的岩石孔隙面积为
| $ \frac{{\rm d}F_{\rm wp}}{{\rm d}r}=-\frac{{\rm d}p}{{\rm d}r}\phi $ | (6) |
式中:
考虑射孔孔眼附近流体的压力梯度和油井产量与生产压差的关系,可得
| $ \left\{ \begin{array}{l} {{F}_{\rm wp}}=\lambda \left[ {{p}_{\rm e}}-{{p}_{\rm wf}}\left( t \right) \right] \\ \lambda =\frac{{{K}_{\rm f}}h}{{{n}_{\rm p}}{{h}_{\rm p}}{{K}_{\rm dp}}{{L}_{\rm p1}}\left( \ln \frac{{{r}_{\rm e}}}{{{r}_{\rm w}}}+{{S}_{\rm d}} \right)}\phi \ln \frac{1}{2{{n}_{\rm p}}{{r}_{\rm p}}} \end{array} \right. $ | (7) |
式中:
考虑流体摩擦拖曳力影响时,射孔孔壁处附加应力为
| $ {{\sigma }_{\rm rw}}=-\lambda \left[ {{p}_{\rm e}}-{{p}_{\rm wf}}\left( t \right) \right] $ | (8) |
式中:
流体摩擦拖曳力主要由生产压差引起,其方向由储层指向射孔孔眼,同流体流动方向一致,同时还与储层孔渗特性、射孔参数等有关。
2.1.3 含水率变化的影响研究表明,含水率对岩石单轴抗压强度的影响满足指数关系[11, 13, 19],即
| $ {{\sigma }_{\rm c}}=M {{\rm e}^{N\cdot {{S}_{\rm w}}}}=M {{\rm e}^{N\cdot {{S}_{\rm w}}(t)}} $ | (9) |
式中:
泥质含量不变时,随着含水率上升,黏土矿物水化膨胀,岩石强度降低。所以对于特定区块或油井,可通过取样进行不同含水率实验下强度变化测试,即可得含水率对岩石单轴抗压强度的影响。
2.1.4 出砂判别准则综上,考虑由生产压差和流体黏度引起的摩擦拖曳力影响,射孔孔眼壁面有效应力分布为
| $ \left\{ \begin{array}{l} {{\sigma }_{{\rm s}}}={{\sigma }_{{\rm se}}}+{{\sigma }_{{\rm rw}}} \\ {{\sigma }_{{\rm{\Psi }} {\rm e}}}=\left( {{\sigma }_{{\rm{ \mathsf{ θ} e}}}}\!+\!{{\sigma }_{\rm ze}} \right)-\\{\kern 40pt}2({{\sigma }_{{\rm{ \mathsf{ θ} e}}}}\!-\!{{\sigma }_{\rm ze}})\cos~2\psi \!-\!{{p}_{\rm pf}}\left( t \right) \end{array} \right. $ | (10) |
由于疏松砂岩油气藏开采过程中,孔壁地层的破坏通常呈现压性剪切破坏方式,即此时在3个应力中,径向压力及井筒内压常常最小。因此,在研究油气开采过程中孔眼稳定性时,一般仅作剪切屈服判别[22-23]。对某射孔孔眼,Mohr-Coulomb强度判别准则表达式为
| $ {{\sigma }_{{\rm{\Psi }} \rm e}}-{{\sigma }_{\rm se}}\frac{1+\sin \varphi }{1-\sin \varphi }=\frac{2C\cos \varphi }{1-\sin \varphi } $ | (11) |
式中:
令
在定向井模型基础上,结合水平井特点,取
| $ \left\{ \begin{array}{l} {{\sigma }_{x}}={{\sigma }_{\rm v}}{{\sin }^{2}}\beta \\ {{\sigma }_{y}}={{\sigma }_{\rm H1}}{{\sin }^{2}}\beta +{{\sigma }_{\rm H2}}{{\cos }^{2}}\beta \\ {{\sigma }_{z}}={{\sigma }_{\rm H1}}{{\cos }^{2}}\beta +{{\sigma }_{\rm H2}}{{\sin }^{2}}\beta \\ {{\tau }_{yz}}=\sin \beta \cos \beta \left( {{\sigma }_{\rm H1}}-{{\sigma }_{\rm H2}} \right) \\ \end{array} \right. $ | (12) |
将原地应力分量代入定向井井周应力分量模型,得水平井井壁周向应力分布
| $ \left\{ \begin{array}{l} {{\sigma }_{\rm re}}=\frac{{{\sigma }_{x}}+{{\sigma }_{y}}}{2}\left (1-\frac{r_{\rm w}^{2}}{{{r}^{2}}}\right )+\frac{{{\sigma }_{x}}-{{\sigma }_{y}}}{2}\left (1+\frac{3r_{\rm w}^{4}}{{{r}^{4}}}-\frac{4r_{\rm w}^{2}}{{{r}^{2}}}\right )\cos~ 2\theta +{{p}_{\rm wf}}\left( t \right )\frac{r_{\rm w}^{2}}{{{r}^{2}}} \\ {{\sigma }_{{\rm{ \mathsf{ θ} e}}}}=\frac{{{\sigma }_{x}}+{{\sigma }_{y}}}{2}\left (1+\frac{r_{\rm w}^{2}}{{{r}^{2}}}\right )-\frac{{{\sigma }_{x}}-{{\sigma }_{y}}}{2}\left (1+\frac{3r_{\rm w}^{4}}{{{r}^{4}}}\right )\cos~2\theta -{{p}_{\rm wf}}\left( t \right)\frac{r_{\rm w}^{2}}{{{r}^{2}}} \\ {{\sigma }_{\rm ze}}={{\sigma }_{z}}-2\mu \left ({{\sigma }_{x}}-{{\sigma }_{y}}\right )\frac{r_{\rm w}^{2}}{{{r}^{2}}}\cos 2\theta \end{array} \right. $ | (13) |
定向井变为水平井后,流体流向也由向射孔孔眼流动改为直接向井筒流动,其摩擦拖曳力为
| $ \left\{ \begin{array}{l} {{F}_{\rm wp}}=\lambda \left[ {{p}_{\rm e}}-{{p}_{\rm wf}}\left( t \right) \right] \\ \lambda =\frac{\phi }{\left( \ln \frac{{{r}_{\rm e}}}{{{r}_{\rm w}}}+{{S}_{\rm d}} \right)}\ln \frac{{{r}_{\rm e}}}{{{r}_{\rm w}}} \end{array} \right. $ | (14) |
考虑流体拖曳力影响时井周应力为
| $ {{\sigma }_{\rm rw}}=-\lambda \left[ {{p}_{\rm e}}-{{p}_{\rm wf}}\left( t \right) \right] $ | (15) |
将井壁上应力转换为主应力,计算得到
| $ \left\{ \begin{array}{l} {{\sigma }_{1}}\!=\!{{\sigma }_{\rm re}}+{{\sigma }_{\rm rw}} \\ {{\sigma }_{2}}\!=\!\frac{{{\sigma }_{\theta \rm e}}+{{\sigma }_{\rm ze}}}{2}+\frac{\sqrt{{{({{\sigma }_{\theta \rm e}}-{{\sigma }_{\rm ze}})}^{2}}+4\tau _{\theta z}^{2}}}{2} \\ {{\sigma }_{3}}\!=\!\frac{{{\sigma }_{\theta \rm e}}+{{\sigma }_{\rm ze}}}{2}-\frac{\sqrt{{{({{\sigma }_{\theta \rm e}}-{{\sigma }_{\rm ze}})}^{2}}+4\tau _{\theta z}^{2}}}{2} \\ {{\tau }_{\theta z}}\!=\!\sin \beta \cos \beta \left( {{\sigma }_{\rm H1}}-{{\sigma }_{\rm H2}} \right)\left( 1\!+\!\frac{r_{\rm w}^{2}}{r_{{}}^{2}} \right)\cos \theta \end{array} \right. $ | (16) |
式中:
| $ \left\{ \begin{array}{l} F - {{\sigma }_{\rm c}} = 0\\ F = \left[{{\sigma }_{\rm max}}-\alpha \cdot {{p}_{\rm p}}(t)\right] -\\{\kern 35pt}\left[ {{\sigma }_{\rm min}}-\alpha \cdot {{p}_{\rm p}}(t) \right]{\cot}^{2}\left({{45}°}-\frac{\varphi }{2}\right)\\ {{\sigma }_{\rm c}}=2C\cot\left({{45}°}-\frac{\varphi }{2}\right) \end{array} \right. $ | (17) |
式中:
当
基于疏松砂岩储层动态出砂预测模型,建立渤海油田疏松砂岩储层开发开采全生命周期动态出砂预测新方法(图 2),具体流程及步骤如下。
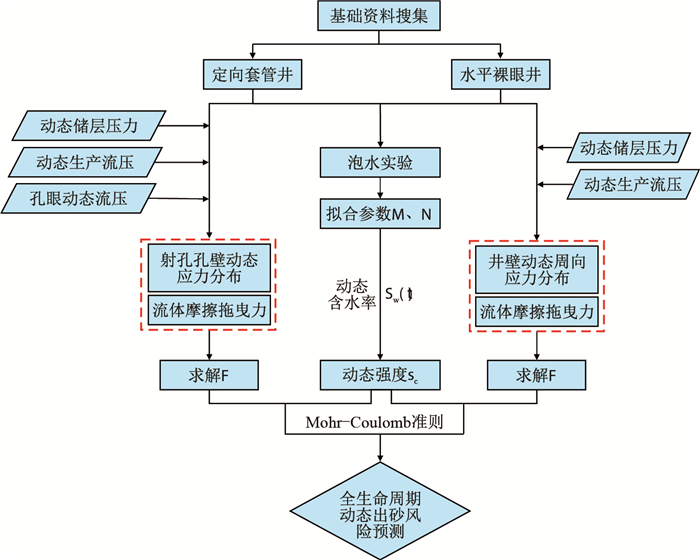 |
| 图2 全生命周期动态出砂预测流程图 Fig. 2 The chart of dynamic sanding prediction new model |
(1) 搜集目的井的基础资料,具体包括:开发层位、测井数据、岩芯、地层水样、油藏开发配产数据、地应力、孔隙度大小等。
(2) 根据目的井的井型和防砂方式选择动态出砂预测模型:定向套管井由式(5)、式(9)分别计算射孔孔壁动态应力分布和动态流体摩擦拖曳力,再计算
(3) 取岩芯和地层水样开展泡水前后的力学强度实验,拟合得参数
(4) 按照前文的判别方法预测储层动态出砂风险,确定储层出砂具体年限和含水率情况,对于早期出砂风险较低的井,可不防砂,后期根据生产情况再调整。
(5) 进一步结合邻井防砂方式、泥质含量、粒度分析等资料确定合理有效的防砂方式。
4 实例分析与应用以X油田为例进行分析,油田主要开采层位为东二下段和东三段,各层位储层性质见表 1。东二下段以水平井为主,东三段以定向井为主,东三段定向井设计采用大孔径射孔弹进行套管射孔完井。取探井岩芯测试岩石泡水前后的单轴抗压强度,求得实验拟合参数
| 表1 X油田储层特性 Tab. 1 The reservoir characteristics of X Oilfield |
| 表2 岩石泡水强度及实验拟合参数 Tab. 2 The parameters of water-saturated rock strength and experimental fitting |
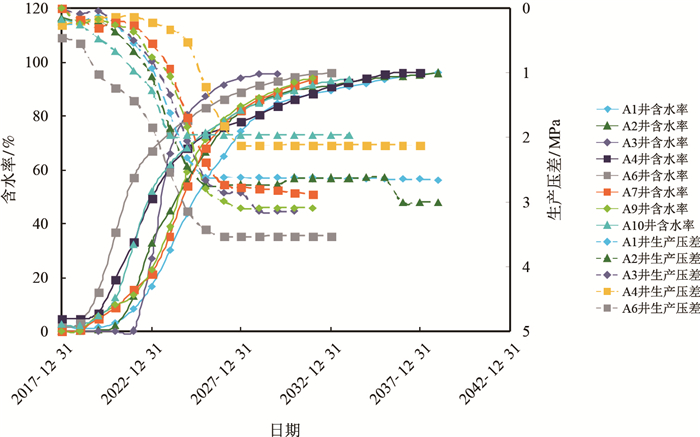
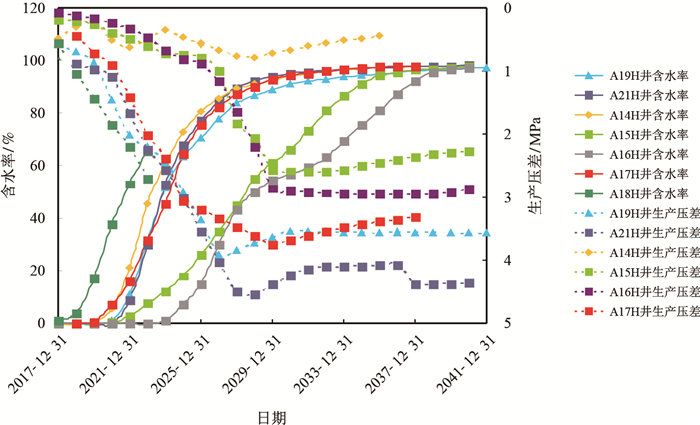
结合油藏配产数据,可得油田动态生产压差和含水率变化曲线,见图 3,图 4。
 |
|
图3
东三段含水率/生产压差动态图
Fig. 3
The moisture content/production pressure differential dynamic figure of E |
 |
|
图4
东二下段含水率/生产压差动态图
Fig. 4
The moisture content/production pressure differential dynamic figure of E |
由图 3,图 4可知,东三段生产压差0
采用疏松砂岩储层动态出砂预测方法,结合配产数据分层位动态出砂预测结果见图 5,图 6。
 |
|
图5
东三段动态出砂预测结果
Fig. 5
Dynamic sand production prediction results of E |
 |
|
图6
东二下段动态出砂预测结果
Fig. 6
Dynamic sand production prediction results of E |
由图 5,图 6可知,东三段定向井投产初期(至少8 a内)无出砂风险,但当含水率上升至65%左右时,油井出砂风险较大;东二下段水平井投产初期储层出砂风险较大,但由于A15H和A16H两口井生产压差较小,同时含水率上升缓慢,因此,这两口井投产初期(9 a内)无出砂风险,后期生产含水率上升至40%左右时,储层出砂风险较大。因此,考虑平台修井能力,东三段定向井和东二下段A15H、A16H两口井投产初期不防砂,其余井需采取防砂措施。
动态法和静态法预测对比结果如表 3所示。由表 3可知,动态法预测出砂风险相对于静态法笼统预测而言更为精细、准确,能细化到具体的生产时间和含水率变化情况。其原因为静态法所采用的泡水后的岩石强度仅为含饱水和度55%时对应的单轴抗压强度,无法代表油井全生命周期的情况,因此,采用某一含水饱和度下的岩石强度作为临界出砂压差去和油藏配产压差对比预测出砂风险的做法较为欠妥。对于东二下段,静态法预测储层处于临界出砂范围,有出砂风险,按照静态法预测保守考虑,该层位井均需采取防砂措施;而采用静态法发现,A15H和A16H两口井投产初期风险较低,可不采取防砂方式,可节省投资约200万元。
| 表3 动态法和静态法预测结果对比 Tab. 3 Prediction result contrast of dynamic and static method |
在动态出砂预测基础上,进一步结合黏土矿物和泥质含量、地层砂粒度分析曲线、临井防砂措施和出砂情况等资料,东三段采用套管射孔完井,不防砂。东二下段采用裸眼完井,除A15H井和A16H井不防砂外,其余井采用优质筛管防砂(挡砂精度30~40目,对应100 μm)。X油田投产表明,各层位出砂风险预判合理、准确,东二下段油井防砂方式和挡砂精度设计合理,未见出砂现象。
5 结论(1) 基于储层动态出砂影响因素及机理分析,以渤海油田常用的定向射孔井和水平裸眼井两种完井方式为研究对象,结合井壁力学,建立了海上疏松砂岩储层全生命周期动态出砂预测方法。
(2) 该预测方法充分考虑了储层地应力、含水率变化、生产压差、储层亏空等因素对储层出砂的动态影响,实现了储层开发生产全过程生命周期中出砂风险的动态预测和分析。
(3) 该方法可有效预测套管射孔井和水平裸眼井动态出砂风险,有助于进一步优化防砂方式,实现降本增效的目的。
| [1] |
刘小利, 夏宏南, 欧阳勇, 等. 出砂预测模型综述[J]. 断块油气田, 2005, 12(4): 59-61. LIU Xiaoli, XIA Hongnan, OUYANG Yong, et al. Overview of sand prediction model[J]. Fault-Block Oil & Gas Field, 2005, 12(4): 59-61. doi: 10.3969/j.issn.1005-8907.2005.04.021 |
| [2] |
夏宏泉, 胡南, 朱荣东. 基于生产压差的深层气层出砂预测[J]. 西南石油大学学报(自然科学版), 2010, 32(6): 79-83. XIA Hongquan, HU Nan, ZHU Rongdong, et al. Sanding prediction of the deep gas reservoir based on producing pressure difference[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(6): 79-83. doi: 10.3863/j.issn.1674-5086.2010.06.016 |
| [3] |
吕广忠, 陆先亮, 栾志安, 等. 油井出砂预测方法研究进展[J]. 油气地质与采收率, 2002, 9(6): 55-57. LÜ Guangzhong, LU Xianliang, LUAN Zhian, et al. The research progress of the well sanding prediction method[J]. Petroleum Geology and Recovery Efficiency, 2002, 9(6): 55-57. doi: 10.3969/j.issn.1009-9603.2002.06.020 |
| [4] |
左星, 申军武, 李薇, 等. 油井出砂预测方法综述[J]. 西部探矿工程, 2006, 18(12): 93-96. ZUO Xing, SHEN Junwu, LI Wei, et al. Overview of the well sanding prediction method[J]. West-China Exploration Engineering, 2006, 18(12): 93-96. doi: 10.3969/j.issn.1004-5716.2006.12.050 |
| [5] |
曾流芳, 刘建军. 裸眼井出砂预测模型的解析分析[J]. 石油钻采工艺, 2002, 24(6): 42-44. ZENG Liufang, LIU Jianjun. Analytical analgsis of sand production model of open-hole completion well[J]. Oil Drilling & Production Technology, 2002, 24(6): 42-44. doi: 10.3969/j.issn.1000-7393.2002.06.016 |
| [6] |
周建良, 李敏, 王平双. 油气田出砂预测方法[J]. 中国海上油气(工程), 1997, 9(4): 26-36. ZHOU Jianliang, LI Min, WANG Pingshuang. Sanding prediction method of oil & gas fied[J]. China Offshore Oil and Gas(Engineering), 1997, 9(4): 26-36. |
| [7] |
董长银, 张清华, 崔明月, 等. 复杂条件下疏松砂岩油藏动态出砂预测研究[J]. 石油钻探技术, 2015, 43(6): 81-86. DONG Changyin, ZHANG Qinghua, CUI Mingyue, et al. A dynamic sanding prediction model for unconsolidated sandstone reserviors with complicated production conditions[J]. Petroleum Drilling Techniques, 2015, 43(6): 81-86. doi: 10.11911/syztjs.201506015 |
| [8] |
祁大晟, 项琳娜, 裴柏林. 塔里木东河油田出砂动态预测研究[J]. 新疆石油地质, 2008, 29(3): 341-343. QI Dasheng, XIANG Linna, PEI Bailin. Study on dynamic sanding prediction in Donghe Oilfiled, Tarim Basin[J]. Xingjiang Petroleum Geology, 2008, 29(3): 341-343. |
| [9] |
赵益忠, 孙德旭, 梁伟, 等. 考虑开发动态的定性经验出砂动态预测[J]. 石油钻采工艺, 2013, 35(5): 67-70. ZHAO Yizhong, SUN Dexun, LIANG Wei, et al. Research on qualitative experimental dynamic sanding prediction considering the development performance[J]. Oil Drilling & Production Technology, 2013, 35(5): 67-70. doi: 10.3969/j.issn.1000-7393.2013.05.020 |
| [10] |
王艳辉, 刘希圣, 王鸿勋. 油井出砂预测技术的发展与应用综述[J]. 石油钻采工艺, 1994, 16(5): 79-85. WANG Yanhui, LIU Xisheng, WANG Hongxun. The technology to predict the sand production of oil well and its applications[J]. Oil Drilling & Production Technology, 1994, 16(5): 79-85. doi: 10.3969/j.issn.1000-7393.1994.05.019 |
| [11] |
VEEKEN C A, DAVIES D R, KENTER C J. Sand production prediction review: Developing an intergrated approach[C]. SPE 22792-MS, 1991. doi: 10.2118/22792-MS
|
| [12] |
TIXIER M P, LOVELESS G W, ABDERSON R A. Estimation strength form the mechanical properities log[J]. JPT, 1975, 27(3): 283-293. doi: 10.2118/4532-PA |
| [13] |
练章华, 刘永刚, 张元泽, 等. 油气井出砂预测研究[J]. 钻采工艺, 2003, 26(5): 30-31, 36. LIAN Zhanghua, LIU Yonggang, ZHANG Yuanze, et al. Application of plastic strain on sand production prediction in oil well[J]. Drilling & Production Technology, 2003, 26(5): 30-31, 36. doi: 10.3969/j.issn.1006-768X.2003.05.011 |
| [14] |
王小鲁, 杨万萍, 严焕德, 等. 疏松砂岩出砂机理与出砂临界压差计算方法[J]. 天然气工业, 2009, 29(7): 72-75. WANG Xiaolu, YANG Wanping, YAN Huande, et al. The sanding mechanism and sanding critical drawdown calculation in loose sandstone[J]. Natural Gas Industry, 2009, 29(7): 72-75. doi: 10.3787/j.issn.1000-0976.2009.07.022 |
| [15] |
雷征东, 李相方, 程时清. 考虑拖曳力的出砂预测新模型及应用[J]. 石油钻采工艺, 2006, 28(1): 69-73. LEI Zhengdong, LI Xiangfang, CHEN Shiqing. Modeling and application to sand prediction considering of drag force[J]. Oil Drilling & Production Technology, 2006, 28(1): 69-73. doi: 10.3969/j.issn.1000-7393.2006.01.019 |
| [16] |
张建国, 程远方, 崔红英. 裸眼完井出砂预测模型的建立[J]. 石油钻探技术, 1999, 27(6): 39-41. ZHANG Jianguo, CHEN Yuanfang, CUI Hongying. The establishment of the open hole completion sanding prediction model[J]. Petroleum Drilling Techniques, 1999, 27(6): 39-41. doi: 10.3969/j.issn.1001-0890.1999.06.016 |
| [17] |
伍葳, 林海, 谭蕊, 等. 压力衰竭对临界生产压差的影响及油藏产能评价[J]. 科学技术与工程, 2013, 23(13): 6825-6834. WU Wei, LIN Hai, TAN Rui, et al. The influence of pressure depletion on critical producing pressure differential and productivity evaluation of reservoirs[J]. Science Technology and Engineering, 2013, 23(13): 6825-6834. doi: 10.3969/j.issn.1671-1815.2013.23.031 |
| [18] |
孙强, 姜春露, 朱术云, 等. 饱水岩石水稳试验及力学特性研究[J]. 采矿与安全工程学报, 2011, 28(2): 236-240. SUN Qiang, JIANG Chunlu, ZHU Shuyun, et al. Water stability test and mechanical property of water saturated rocks[J]. Journal of Mining & Safety Engineering, 2011, 28(2): 236-240. doi: 10.3969/j.issn.1673-3363.2011.02.013 |
| [19] |
林海, 邓金根, 胡连波, 等. 含水率对岩石强度及出砂影响研究[J]. 科学技术与工程, 2013, 13(13): 3710-3713. LIN Hai, DENG Jingen, HU Lianbo, et al. Study on the effect of water content on rock strength and sand production[J]. Science Technology and Engineering, 2013, 13(13): 3710-3713. doi: 10.3969/j.issn.1671-1815.2013.13.036 |
| [20] |
郭云民, 李健康, 崔洁, 等. 高含水期油井出砂预测模型的研究与应用[J]. 油气地质与采收率, 2005, 12(3): 58-61. GUO Yunmin, LI Jiankang, CUI Jie, et al. Research and application of sanding prediction model for high water-cut oil wells[J]. Petroleum Geology and Recovery Efficiency, 2005, 12(3): 58-61. doi: 10.3969/j.issn.1009-9603.2005.03.018 |
| [21] |
王彦利, 陈小凡, 邓生辉, 等. 疏松砂岩临界出砂压差的计算方法研究及应用[J]. 西南石油大学学报(自然科学版), 2009, 31(1): 78-80. WANG Yanli, CHEN Xiaofan, DENG Shenghui, et al. The calculation method study and application of the critical sand production pressure difference in loose sandstone[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(1): 78-80. doi: 10.3863/j.issn.1674-5086.2009.01.019 |
| [22] |
刘向君, 罗平亚. 岩石力学与石油工程[M]. 北京: 石油工业出版社, 2004. LIU Xiangjun, LUO Pingya. Rock mechanics and petroleum engineering[M]. Beijing: Petroleum Industry Press, 2004. |
| [23] |
练章华, 杨龙, 段永刚, 等. 塑性应变准则在油井出砂预测中的应用[J]. 西南石油学院学报, 2003, 25(4): 16-18. LIAN Zhanghua, YANG Long, DUAN Yonggang, et al. Application of plastic strain on prediction of sand production in oil well[J]. Journal of Southwest Petroleum Insititute, 2003, 25(4): 16-18. doi: 10.3863/j.issn.1674-5086.2003.04.005 |
 2019, Vol. 41
2019, Vol. 41


