喷射器是利用工作流体来传递能量和质量的真空获得装置,它是采用有一定压力的工作气体经过工作喷嘴时,速度急剧增大,使得喷嘴出口区域的压力极大降低,造成真空从而抽吸流体。其主要优点是不消耗机械能,结构简单,没有运动部件,不易损坏[1-2],在石油天然气开采、化工、轻工、制冷等工业技术领域获得了越来越广泛的应用[3-8],尤其一些特殊生产工艺,如真空蒸馏、真空干燥和真空结晶等,应用前景广阔[3, 5]。
喷射器的研究历史很长,喷射器的理论在长达一个世纪的研究周期内日趋完善。19世纪80年代,德国学者Zeuner和Rankin的著作打开了喷射器理论的先河[9],但是该理论也存在缺陷,就是不能解决喷射器的设计问题,直到20世纪30年代流体力学和空气动力学科的飞速发展,才使得喷射器的应用与研究工作有了质的飞跃。早期学者对喷射器的研究为之后理论发展提供了有力的基础[10-15]。索科洛夫在前人的基础上,通过大量实验,逐步建立起适用于不同领域和工况范围的喷射器理论,索科洛夫在其著作中对喷射器的设计方法有着详尽的阐述,在喷射器动量守恒、质量守恒和能量守恒的基础上,通过引入气体动力学函数来建立与热力学参数之间的联系,分别推导了适合不同类型喷射器特点的基本方程[16]。索科洛夫的气体动力函数法于20世纪60年代传入中国,给中国的喷射器设计带来了很好的规范,并对中国喷射器的理论研究及发展产生了深远影响[3, 17-22]。
由于喷射器内实际流动情况的复杂性,在建立喷射器数学模型时为简化推导过程,都会做一些假设。索科洛夫在其设计方法中的一个重点假定就是气体介质为理想气体,气体动力学函数理论式和基本方程的推导都是基于这个假定进行的。众所周知,喷射器的很多工业应用中,操作压力范围涉及低压到高压全范围,在低压情况下,这个假定没有任何问题,但是在压力较大的情况下,比如在石油、天然气的喷射举升过程中,天然气进口压力非常大,甚至高达数十兆帕,这么大的压力,理想气体状态方程已经不再适用,此时索科洛夫设计理论所设计的喷射器将与实际存在偏差。为此,本文对索科洛夫的气体动力函数法从真实气体角度进行了修正,提出真实气体的气体动力学函数理论式,鉴于很多学者已在中压缩比与大压缩比的喷射器研究中考虑了真实气体并得出相关结论[23-29],本文研究侧重点放在小压缩比的喷射器(气体喷射器与气力输送喷射器),对设计计算中常用到的特性曲线方程、最佳面积比方程和喷射系数方程以真实气体的气体动力学函数理论式为基础重新进行了推导,并与索科洛夫设计方法进行对比研究,基于真实气体的修正弥补了索科洛夫设计方法的局限,可适用于全压范围的喷射器设计。
1 真实气体的气体动力学函数推导气体动力学函数理论式是整个喷射器理论的关键,在索科洛夫设计方法中,所给出的气体动力函数理论式全部以理想气体关系式为推导前提,那么,推导出基于真实气体的气体动力学函数理论式显得尤为重要。
若取温度和压力为独立变量,焓可以表示为温度和压力的函数
| $ h=f( T, p ) $ | (1) |
式中:
由式(1)进行热力学偏导数变换时,存在如下全微分关系式
| $ {\rm d}h={{\left( \dfrac{\partial h}{\partial T} \right)}_{{\rm p}}}{\rm d}T+{{\left( \dfrac{\partial h}{\partial p} \right)}_{{\rm T}}}{\rm d}p $ | (2) |
式中:下标p—等压过程;
下标T—等温过程。
同时焓
| $ {\rm d}h=T{\rm d}s+v{\rm d}p $ | (3) |
式中:
联立式(2),式(3),可得
| $ {{\left( \dfrac{\partial h}{\partial p} \right)}_{{\rm T}}}=T{{\left( \dfrac{\partial s}{\partial p} \right)}_{{\rm T}}}+v $ | (4) |
根据Maxwell关系式和定压比热容
| $ {{\left( \dfrac{\partial s}{\partial p} \right)}_{{\rm T}}}=-{{\left( \dfrac{\partial v}{\partial T} \right)}_{{\rm p}}} $ | (5) |
| $ {{c}_{{\rm p}}}={{\left( \dfrac{\partial h}{\partial p} \right)}_{{\rm T}}} $ | (6) |
式中:
将式(4)~式(6)代入式(2),可得
| $ {\rm d}h={{c}_{{\rm p}}}{\rm d}T+\left[ v-T{{\left( \dfrac{\partial v}{\partial T} \right)}_{{\rm p}}} \right]{\rm d}p $ | (7) |
按等熵过程将式(7)两边除以d
| $ {{\left( \dfrac{\partial h}{\partial T} \right)}_{\rm s}}={{c}_{\rm p}}+\left[ v-T{{\left( \dfrac{\partial v}{\partial T} \right)}_{\rm p}} \right]{{\left( \dfrac{\partial p}{\partial T} \right)}_{\rm s}} $ | (8) |
式中:下标s—等熵过程。
将式(8)右边的偏导数部分通过推证法求得[30]
| $ {{\left( \dfrac{\partial p}{\partial T} \right)}_{{\rm s}}}=\dfrac{{{c}_{{\rm p}}}}{{{\alpha }_{{\rm p}}}vT} $ | (9) |
| $ {{\left( \dfrac{\partial v}{\partial T} \right)}_{{\rm p}}}={{\alpha }_{{\rm p}}}v $ | (10) |
式中:
将式(6),式(9)及式(10)代入式(8),有
| $ {{\left( \dfrac{\partial h}{\partial T} \right)}_{{\rm s}}}=\dfrac{{{c}_{\rm p}}}{{{\alpha }_{\rm p}}T} $ | (11) |
真实气体在等熵过程中,温度、压力及比容的变化满足以下两个关系式[31]
| $ p{{v}^{{{k}_{{\rm v}}}}}=\rm const $ | (12) |
| $ T{{p}^{-\frac{{{k}_{{\rm T}}}-1}{{{k}_{{\rm T}}}}}}=\rm const $ | (13) |
式中:
由热力学微分关系,
| $ {{c}_{{\rm p}}}=\dfrac{{{k}_{{\rm T}}}}{{{k}_{{\rm T}}}-1}R{{Z}_{{\rm T}}} $ | (14) |
式中:R—普适气体常数,R=8.314 J/(K
导数压缩因子
| $ {{Z}_{{\rm T}}}=\dfrac{p}{R}{{\left( \dfrac{\partial v}{\partial T} \right)}_{{\rm p}}} $ | (15) |
将式(10),式(15)代入式(14),有
| $ {{c}_{{\rm p}}}=\dfrac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}{{\alpha }_{{\rm p}}}pv $ | (16) |
将式(16)代入式(11),可得
| $ {{\left( \dfrac{\partial h}{\partial T} \right)}_{\rm s}}=\dfrac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}\dfrac{pv}{T}=\dfrac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}ZR $ | (17) |
将式(17)按等熵过程积分,有
| $ {h_0} - h = \int_T^{{T_0}} {\frac{{{k_{\rm{T}}}}}{{{k_{\rm{T}}} - 1}}ZR} $ | (18) |
式中:
假设滞止状态压缩因子在温度改变过程中呈线性变化,则给定状态与临界状态时的压缩因子可用相应的系数来修正
| $ \left \{ \begin{array}{l} Z_{{\rm 1}}=mZ \\ Z_{{\rm {\ast}}}=nZ \end{array} \right . $ | (19) |
式中:
等熵过程中,气体一维稳定流动的能量方程微分式
| $ {\rm d}h+{\rm d}\left( \dfrac{{{\omega }^{2}}}{2} \right)=0 $ | (20) |
式中:
声速传播是一个绝热过程,则真实气体声速可表示为
| $ a={{\sqrt{\left( \dfrac{\partial p}{\partial \rho } \right)}}_{\rm s}}=\sqrt{{{k}_{\rm v}}pv} $ | (21) |
式中:
将式(18),式(21)代入式(20),并做相应的变换,可得
| $ \dfrac{{{T}_{0}}}{T}=m\left[ 1+\dfrac{{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{2{{k}_{\rm T}}}M_{\rm a}^{2} \right] $ | (22) |
式中:
由于气体动力学函数把气体等熵速度与热力学参数联系起来,引入折算等熵速度
| $ \tau \left( \lambda \right)=\dfrac{1}{m}\left[ 1-\dfrac{{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{{\lambda }^{2}} \right] $ | (23) |
| $ \varPi \left( \lambda \right)=\tau \left( \lambda \right)^{\frac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}} $ | (24) |
| $ \varepsilon \left( \lambda \right)=\tau \left( \lambda \right)^{\frac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}\frac{1}{{{k}_{\rm v}}}} $ | (25) |
式中:
当气体等熵流动速度等于临界速度
| $ {{\tau }_{{\ast}}}\left( \lambda \right)=\dfrac{1}{n}\dfrac{2{{k}_{\rm T}}}{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)} $ | (26) |
| $ {{\varPi }_{{\ast}}}\left( \lambda \right)= {{\tau }_{{\ast}}}\left( \lambda \right)^{\frac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}} $ | (27) |
| $ {{\varepsilon }_{{\ast}}}\left( \lambda \right)= {{\tau }_{{\ast}}}\left( \lambda \right)^{\frac{{{k}_{\rm T}}}{{{k}_{\rm T}}-1}\frac{1}{{{k}_{\rm v}}}} $ | (28) |
式中:
把将式(26),式(27)代入式(21),真实气体的临界速度方程为
| $ {{a}_{{\ast}}}=\sqrt{\dfrac{2{{k}_{\rm v}}{{k}_{\rm T}}{{p}_{0}}{{v}_{0}}}{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}} $ | (29) |
式中:
喷射器数学模型涉及的基本方程包括特性曲线、最佳面积比和喷射系数方程。小压缩比的(压缩比小于1.2)气体喷射器在拟定基本方程时,因为引射介质与混合介质的压缩比很小,可将它们视为非弹性介质,因此与气力输送输送喷射器(气力输送液体或固体颗粒)原则上方程可以通用,重点区别在于气力输送喷射器的工作气体与引射介质相态不同。
2.1 特性曲线方程特性曲线方程的形式取决于工作气体的膨胀比和喷射器是否带扩散器。当工作气体为超临界膨胀比时,工作喷嘴要采用拉瓦尔喷嘴,而当工作气体为亚临界膨胀比时,工作喷嘴需采用锥形喷嘴[16]。文中以研究带扩散器的超临界膨胀比喷射器为主,对于工作气体为亚临界膨胀比的情况,所有推导结果可通过用折算质量速度与喷嘴出口截面面积乘积代替喷嘴临界截面面积并做相应变换之后得到,因此不再赘述。
2.1.1 数学模型建立的假设条件为简化推导过程,在建立喷射器数学模型时做如下假设。
(1) 喷射器内为一维稳态流动。
(2) 工作气体通过喷射器时与外界的热交换忽略不计。
(3) 将工作喷嘴、引射入口、混合室和扩散器内的介质流动过程近似为等熵过程,不可逆因素由速度系数修正。
(4) 工作气体和引射介质在工作喷嘴出口(1-1截面)与混合室入口(2-2截面)之间段上不相混合(图 1)。
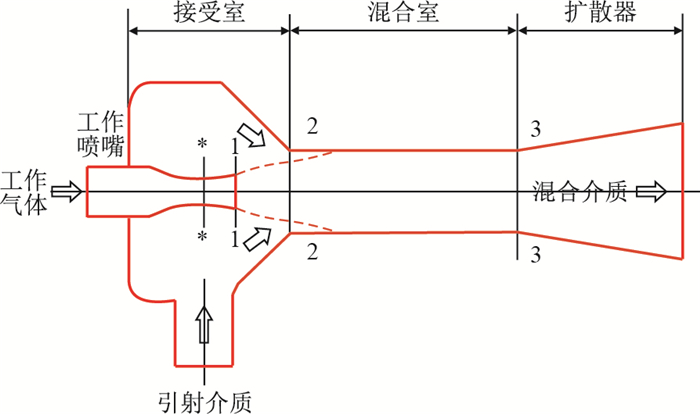 |
| 图1 喷射器结构图 Fig. 1 Structure diagram of ejector |
如图 1所示,在2-2和3-3截面之间的圆柱形混合室部分建立动量方程
| $ {{\phi }_{2}}\left( {{G}_{\rm P}}{{\omega }_{\rm P2}}+{{G}_{\rm H}}{{\omega }_{\rm H2}} \right)+{{p}_{\rm P2}}{{A}_{\rm P2}}+{{p}_{\rm H2}}{{A}_{\rm H2}} = \\ {\kern 20pt}\left( {{G}_{\rm P}}+{{G}_{\rm H}} \right){{\omega }_{3}}+{{p}_{3}}{{A}_{3}} $ | (30) |
式中:
工作气体和引射介质在输入管道中的初速度以及喷射器出口处混合介质的速度与它们在混合室中的速度相比很小,可认为喷射器的工作气体、引射介质入口与混合介质出口为滞止状态。
2.1.2 工作气体参数的确定在混合室入口截面处工作气体速度可用式(31)表示[16]
| $ {{\omega }_{\rm P2}}={{\phi }_{1}}{{a}_{\rm P{\ast}}}{{\lambda }_{\rm P2}} $ | (31) |
式中:
工作气体质量流量,由连续性方程直接以临界状态的热力学参数代入定义式来确定
| $ {{G}_{\rm P}}=\dfrac{{{A}_{\rm P{\ast}}}{{a}_{\rm P{\ast}}}}{{{v}_{\rm P{\ast}}}} $ | (32) |
式中:
将式(27)~式(29)代入式(32),工作气体质量流量
| $ \left \{ \begin{array}{l} {{G}_{\rm P}}=\dfrac{K{{p}_{\rm P}}\varPi _{\rm P{\ast}}^{\prime }{{A}_{\rm P{\ast}}}}{{{a}_{\rm P{\ast}}}} \\ K=n{{k}_{\rm v}} \\ \varPi _{\rm P{\ast}}^{\prime }={{ {{\varPi }_{\rm P{\ast}}} }^{\frac{{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{{{k}_{\rm T}}{{k}_{\rm v}}}}} \end{array} \right . $ | (33) |
式中:
根据质量守恒和喷射系数定义,有
| $ {{G}_{\rm c}}={{G}_{\rm P}}+{{G}_{\rm H}}={{G}_{\rm P}}\left( 1+u \right) $ | (34) |
式中:
在推导特性曲线方程时,常用到气体动力学函数中的折算质量速度,根据定义,折算质量速度为在给定截面上等熵流动流体的质量速度与在临界截面上这种流体的质量速度之比[16]
| $ q=\dfrac{\omega {{v}_{{\ast}}}}{v{{a}_{{\ast}}}} $ | (35) |
式中:
并且根据介质的质量守恒条件,折算质量速度也等于流体的临界截面与给定截面的面积之比[16]
| $ q=\dfrac{{{A}_{{\ast}}}}{A} $ | (36) |
式中:
超临界膨胀比时气体的弹性特性应该予以考虑,气体喷射器在小压缩比的情况下,在拟定基本方程时,因为引射气体和混合气体的压缩比很小,可以把它们都视为非弹性介质,在等熵过程中,气体在非弹性条件下的气体动力学函数计算式可引申用于气力输送喷射器中引射介质(液体或固体颗粒)和混合介质(气液或气固混合物)的计算[16]。
非弹性介质在理想状态下,等熵过程比容与压力的关系式[16]
| $ {{p}^{\frac{1}{k}}}v= \rm const $ | (37) |
式中:
等熵改变压力的过程,根据式(37),绝热指数
临界速度
| $ {{a}_{{\ast}}}=\sqrt{2{{p}_{0}}{{v}_{0}}} $ | (38) |
折算等熵速度λ
| $ \lambda =\dfrac{\omega }{{{a}_{{\ast}}}}=\sqrt{1-\dfrac{p}{{{p}_{0}}}} $ | (39) |
折算质量速度
| $ q=\dfrac{\omega {{v}_{{\ast}}}}{v{{a}_{{\ast}}}}=\lambda $ | (40) |
相对压力
| $ \varPi =\dfrac{p}{{{p}_{0}}}=1-{{\lambda }^{2}}=1-\dfrac{{{p}_{0}}-p}{{{p}_{0}}} $ | (41) |
由于混合室入口截面处工作气体与引射介质的静压力
| $ {{p}_{\rm P2}}={{\varPi }_{\rm P2}}{{p}_{\rm P}} $ | (42) |
| $ {{p}_{\rm H2}}={{\varPi }_{\rm H2}}{{p}_{\rm H}} $ | (43) |
| $ {{p}_{3}}={{\varPi }_{\rm c3}}{{p}_{\rm c}} $ | (44) |
式中:
根据式(36),式(37)~(40),引射介质在混合室入口截面与混合介质在混合室出口截面上的真实气体折算等熵速度与折算质量速度为
| $ {\lambda _{\rm H2}} = {q_{\rm H2}} = K\dfrac{{{A_{\rm P{\ast}}}}}{{{A_{\rm H2}}}}\dfrac{{\varPi _{\rm P{\ast}}^\prime }}{2} \sqrt {\dfrac{{{p_{\rm P}}{v_{\rm H}}}}{{{p_{\rm H}}{v_{\rm P}}}}} \cdot \\{\kern 20pt}\sqrt {\dfrac{{2{k_{\rm T}} + {k_{\rm v}}\left( {{k_{\rm T}} - 1} \right)}}{{{k_{\rm T}}{k_{\rm v}}}}}{\kern 1pt} u $ | (45) |
| $ {\lambda _{\rm c3}} = {q_{\rm c3}} = K\dfrac{{{A_{\rm P{\ast}}}}}{{{A_{\rm H2}}}}\dfrac{{\varPi _{\rm P{\ast}}^\prime }}{2} \sqrt {\dfrac{{{p_{\rm P}}{v_{\rm c}}}}{{{p_{\rm c}}{v_{\rm P}}}}} {\kern 1pt} \left( {1 + u} \right)\cdot \\ {\kern 20pt} \sqrt {\dfrac{{2{k_{\rm T}} + {k_{\rm v}}\left( {{k_{\rm T}} - 1} \right)}}{{{k_{\rm T}}{k_{\rm v}}}}} $ | (46) |
式中:
根据式(41)、式(45)及式(46),则可确定出式式(43)和式(44)中引射介质在混合室入口截面与混合介质在混合室出口截面处的相对压力
| $ {{\varPi }_{\rm H2}}=\dfrac{{{p}_{\rm H2}}}{{{p}_{\rm H}}}=1-\lambda _{\rm H2}^{2}=1-q_{\rm H2}^{2} $ | (47) |
| $ {{\varPi }_{\rm c3}}=\dfrac{{{p}_{3}}}{{{p}_{\rm c}}}=1-\lambda _{\rm c3}^{2}=1-q_{\rm c3}^{2} $ | (48) |
根据式(38)及式(39),可推出用于计算引射介质在混合室入口截面与混合介质在混合室出口截面的等熵速度
| $ {{\omega }_{\rm H2}}={{\phi }_{4}}{{a}_{\rm H{\ast}}}{{\lambda }_{\rm H2}} $ | (49) |
| $ {{\omega }_{3}}=\dfrac{{{a}_{\rm c{\ast}}}}{{{\phi }_{3}}}{{\lambda }_{\rm c3}} $ | (50) |
式中:
在喷射器的设计中,速度系数
确定引射介质和混合介质的比容是计算不同相喷射器的独有特点。如果气力输送喷射器引射介质是液体或固体和气体的混合物,那么,引射介质的比容为
| $ {{v}_{\rm H}}={{v}_{\rm H\Gamma }}\dfrac{{{u}_{\Gamma }}}{{{u}_{\Gamma }}+{{u}_{\rm t}}}+{{v}_{\rm t}}\dfrac{{{u}_{\rm t}}}{{{u}_{\Gamma }}+{{u}_{\rm t}}} $ | (51) |
式中:
喷射器出口处混合介质的比容则可用工作气体和引射介质的质量分数来表示
| $ {{v}_{\rm c}}={{v}_{\rm c\Gamma }}\dfrac{1}{1+u}+{{v}_{\rm H}}\dfrac{u}{1+u} $ | (52) |
式中:
式(51)中,气力输送喷射器总喷射系数要充分考虑引射介质的组成
| $ u={{u}_{\Gamma }}+{{u}_{\rm t}} $ | (53) |
把工作气体、引射介质和混合介质参数全部代入动量方程式(式(30)),考虑到非弹性介质条件下压缩比对结果精度的影响,引入引射介质相对压降
| $ \left \{ \begin{array}{l} \dfrac{{\Delta {p_{\rm c}}}}{{{p_{\rm H}}}} = \dfrac{{{A_{\rm P {\ast}}}}}{{{A_3}}}\dfrac{{{p_{\rm P}}}}{{{p_{\rm H}}}}\left[ {{\phi _1}{\phi _2}K\varPi _{\rm P {\ast}}^\prime {\lambda _{\rm PH}} + \dfrac{{{A_{\rm P {\ast}}}}}{{{A_{\rm H2}}}}\gamma \varPi {{_{\rm P {\ast}}^\prime }^2} \left( {{\phi _2}{\phi _4} - 0.5} \right)\dfrac{{{v_{\rm H}}}}{{{v_{\rm P}}}}{u^2}{\kern 1pt} -\\ \dfrac{{{A_{\rm P {\ast}}}}}{{{A_3}}}\gamma {{ {\varPi _{\rm P {\ast}}^\prime } }^2}\left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\dfrac{{{v_{\rm c}}}}{{{v_{\rm P}}}}{{\left( {1 + u} \right)}^2}} \right] \\[3pt] \gamma ={{K}^{2}}\dfrac{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{2{{k}_{\rm T}}{{k}_{\rm v}}} \end{array} \right . $ | (54) |
| $ \dfrac{{\Delta {p_{\rm c}}}}{{{p_{\rm H}}}}\dfrac{{{A_3}}}{{{A_{\rm P {\ast}}}}}\dfrac{{{p_{\rm H}}}}{{{p_{\rm P}}}} = {\phi _1}{\phi _2}K\varPi _{\rm P {\ast}}^\prime {\lambda _{\rm PH}} + \dfrac{{{A_{\rm P {\ast}}}}}{{{A_{\rm H2}}}}\gamma {\left( {\varPi _{\rm P {\ast}}^\prime } \right)^2}\left( {{\phi _2}{\phi _4} - 0.5} \right)\\ \left( {\dfrac{{{v_{\rm H\Gamma }}}}{{{v_{\rm P}}}}{u_\Gamma } + \dfrac{{{v_{\rm t}}}}{{{v_{\rm P}}}}{u_{\rm t}}} \right)\left( {{u_\Gamma } + {u_{\rm t}}} \right){\kern 1pt} - \\[1pt] {\kern 20pt}\dfrac{{{A_{\rm P {\ast}}}}}{{{A_3}}}\gamma {\left( {\varPi _{\rm P {\ast}}^\prime } \right)^2}\left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\left( {1 + {u_\Gamma } + {u_{\rm t}}} \right)\left[ {\dfrac{{{v_{c.\Gamma }}}}{{{v_{\rm P}}}}\left( {1 + {u_\Gamma }} \right) + \dfrac{{{v_{\rm t}}}}{{{v_{\rm P}}}}{u_{\rm t}}} \right] $ | (55) |
式中:
在索科洛夫设计理论中,小压缩比的气体喷射器与气力输送喷射器,混合室形状为圆柱形,面积比(
| $ {\left( {\dfrac{{{A_3}}}{{{A_{\rm P*}}}}} \right)_{{\rm{OP{\rm T}}}}}{\left( {\dfrac{{2\gamma \varPi _{\rm P*}^\prime }}{{{\phi _1}{\phi _2}K{\lambda _{{\rm{PH}}}}}}} \right)^{ - 1}} \!= \! \left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\dfrac{{{v_{\rm{c}}}}}{{{v_{\rm{P}}}}}{\left( {1 + u} \right)^2} - \\ \left( {{\phi _2}{\phi _4} - 0.5} \right)\dfrac{{{A_{\rm{3}}}}}{{{A_{{\rm{H2}}}}}}\dfrac{{{v_{\rm{H}}}}}{{{v_{\rm{P}}}}}{u^2} $ | (56) |
| $ {\left( {\dfrac{{{A_3}}}{{{A_{{\rm{P}}*}}}}} \right)_{{\rm{OP{\rm T}}}}}{\left( {\dfrac{{2\gamma \varPi _{P*}^\prime }}{{{\phi _1}{\phi _2}K{\lambda _{{\rm{PH}}}}}}} \right)^{ - 1}} = \left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\left[ {\dfrac{{{v_{{\rm{c\Gamma }}}}}}{{{v_{\rm{P}}}}}\left( {1 + {u_{\rm{\Gamma }}}} \right) + \dfrac{{{v_t}}}{{{v_{\rm{P}}}}}{u_{\rm{t}}}} \right]\\ \left( {1 + u} \right) - \dfrac{{{A_3}}}{{{A_{{\rm{H2}}}}}}\left( {{\phi _2}{\phi _4} - 0.5} \right)\left( {\dfrac{{{v_{{\rm{H\Gamma }}}}}}{{{v_{\rm{P}}}}}{u_{\rm{\Gamma }}} + \dfrac{{{v_{\rm{t}}}}}{{{v_{\rm{P}}}}}{u_{\rm{t}}}} \right)u $ | (57) |
式中:
式(56),式(57)中,
| $ \dfrac{{{A}_{3}}}{{{A}_{\rm H2}}}=\dfrac{\dfrac{{{A}_{3}}}{{{A}_{\rm P{\ast}}}}}{\dfrac{{{A}_{3}}}{{{A}_{P{\ast}}}}-\dfrac{1}{{{q}_{\rm PH}}}} $ | (58) |
式中:
计算中,
| $ {q_{{\rm{PH}}}} = {\lambda _{{\rm{PH}}}}{\left[ {\dfrac{n}{m}\dfrac{{2{k_{\rm T}} + {k_{\rm v}}\left( {{k_{\rm T}} - 1} \right)}}{{2{k_{\rm T}}}}} \right]^{\frac{{{k_{\rm T}}}}{{{k_{\rm T}} - 1}}\frac{1}{{{k_{\rm v}}}}}}\cdot \\[5pt]{\kern 20pt}{\left( {1 - \dfrac{{{k_{\rm v}}{k_{\rm T}} - {k_{\rm v}}}}{{2{k_{\rm T}} + {k_{\rm v}}{k_{\rm T}} - {k_{\rm v}}}}\lambda _{{\rm{PH}}}^2} \right)^{\frac{{{k_{\rm T}}}}{{{k_{\rm T}} - 1}}\frac{1}{{{k_{\rm v}}}}}} $ | (59) |
工作气体在喷嘴出口处的真实气体折算等熵速度λ
| $ {{\lambda }_{\rm PH}}={{M}_{\rm a1}}\sqrt{\dfrac{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)}{2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)M_{\rm a1}^{2}}} $ | (60) |
式中:
喷嘴出口气体马赫数
| $ {{M}_{a1}}=\sqrt{{{\left( \dfrac{{{p}_{0}}}{p} \right)}^{\frac{{{k}_{\rm T}}-1}{{{k}_{\rm T}}}}}\dfrac{2{{k}_{\rm T}}}{m\left[2{{k}_{\rm T}}+{{k}_{\rm v}}\left( {{k}_{\rm T}}-1 \right)\right ]}} $ | (61) |
式(54)、式(55)在计算喷射器引射介质可达到的相对压降Δ
| $ {\left( {\dfrac{{{A_3}}}{{{A_{\rm P{\ast}}}}}} \right)_{\rm OPT}} = \dfrac{{K\varPi _{\rm P{\ast}}^\prime }}{2}\dfrac{{{p_{\rm P}}{\phi _1}{\phi _2}{\lambda _{\rm PH}}}}{{\Delta {p_{\rm c}}}} $ | (62) |
对于气力输送液体或固体颗粒时,当液体或固体颗粒中不掺有气体的情况下,由于工作气体与引射介质混合过程中不会凝结,再加上气体体积远远大于液体或固体颗粒的体积,那么,喷射器混合室内将被气体流所占据,按照这样的考虑气力输送喷射器则可能会出现第三极限状态,而极限状态下的性能主要取决于面积比[16],此种情况下按式(62)计算出的面积比
第三极限状态下喷射系数方程为
| $ {{\left( {{u}_{\Gamma }} \right)}_{\rm \Pi P_3}}=\dfrac{{{K}_{\rm c}}}{{{K}_{\rm P}}}\dfrac{{{p}_{\rm c}}}{{{p}_{\rm P}}}\dfrac{\varPi _{\rm c{\ast}}^{\prime }}{\varPi _{\rm P{\ast}}^{\prime }}\dfrac{{{a}_{\rm P{\ast}}}}{{{a}_{c{\ast}}}}\dfrac{{{A}_{3}}}{{{A}_{\rm P{\ast}}}}-1 $ | (63) |
式中:
下标
相应于第三极限状态下,混合介质的速度达到临界速度,引射介质中按气体计的极限喷射系数为零时(即引射介质中不掺有气体),式(63)可变成
| $ {{\left( {{p}_{\rm c}} \right)}_{\rm \Pi P_3}}={{p}_{\rm P}}\dfrac{{{A}_{\rm P{\ast}}}}{{{A}_{3}}} $ | (64) |
式中:
将式(62)计算出的最佳面积比
要解决真实气体下的喷射器喷射系数的计算,需要建立喷射系数方程。通过联立特性曲线和最佳面积比方程可求得气体喷射器与气力输送输送喷射器的喷射系数方程
| $ \left[ {\left( {{\phi _2}{\phi _4} - 0.5} \right)\dfrac{{{A_3}}}{{{A_{{\rm{H2}}}}}}\dfrac{{{v_{\rm{H}}}}}{{{v_{\rm{P}}}}} - \left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\dfrac{{{v_{\rm{c}}}}}{{{v_{\rm{P}}}}}} \right]\dfrac{{2\gamma \Delta {p_{\rm{c}}}\Pi _{{\rm{P*}}}^\prime }}{{{p_{\rm{P}}}K{\phi _1}{\phi _2}{\lambda _{{\rm{PH}}}}}}{u^2} \\ + \left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\dfrac{{4{\gamma _c}\Pi _{{\rm{P*}}}^\prime }}{{{p_{\rm{P}}}K{\phi _1}{\phi _2}{\lambda _{{\rm{PH}}}}}}\dfrac{{{v_{\rm{c}}}}}{{{v_{\rm{P}}}}}u + \dfrac{{K\Pi _{{\rm{P*}}}^\prime {\phi _1}{\phi _2}{\lambda _{{\rm{pH}}}}}}{2} - \\[5pt]{\kern 25pt}\left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\dfrac{{{v_{\rm{c}}}}}{{{v_{\rm{P}}}}}\dfrac{{2\gamma \Delta {p_{\rm{c}}}\Pi _{{\rm{P*}}}^\prime }}{{{p_{\rm{P}}}K{\phi _1}{\phi _2}{\lambda _{{\rm{PH}}}}}}=0 $ | (65) |
| $ u = \\ \dfrac{{\left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\left[ {\dfrac{{{v_{{\rm{c\Gamma }}}}}}{{{v_{\rm{P}}}}}\left( {1 + {u_{\rm{\Gamma }}}} \right) + \dfrac{{{v_{\rm{t}}}}}{{{v_{\rm{P}}}}}{u_{\rm{t}}}} \right]\gamma \dfrac{{\Delta {p_{\rm{c}}}}}{{{p_{\rm{P}}}}} - \dfrac{{{{\left( {{\phi _1}{\phi _2}K{\lambda _{{\rm{PH}}}}} \right)}^2}}}{4}}}{{\gamma \dfrac{{\Delta {p_{\rm{c}}}}}{{{p_{\rm{P}}}}}\dfrac{{{A_3}}}{{{A_{{\rm{H2}}}}}}\left( {\dfrac{{{v_{{\rm{H\Gamma }}}}}}{{{v_{\rm{P}}}}}{u_{\rm{\Gamma }}} + \dfrac{{{v_{\rm{t}}}}}{{{v_{\rm{P}}}}}{u_{\rm{t}}}} \right)\left( {{\phi _2}{\phi _4} - 0.5} \right) - \gamma \dfrac{{\Delta {p_{\rm{c}}}}}{{{p_{\rm{P}}}}}\left( {\dfrac{1}{{{\phi _3}}} - 0.5} \right)\left[ {\dfrac{{{v_{{\rm{c\Gamma }}}}}}{{{v_{\rm{P}}}}}\left( {1 + {u_{\rm{\Gamma }}}} \right) + \dfrac{{{v_{\rm{t}}}}}{{{v_{\rm{P}}}}}{u_{\rm{t}}}} \right]}} $ | (66) |
气体喷射器喷射系数方程(式(65))是一元二次方程,计算时应取正根。实际工作中气力输送喷射器引射介质中有可能不掺有气体,即
| $ u=\dfrac{\phi _{1}^{2}\phi _{2}^{2}{{K}^{2}}\lambda _{\rm PH}^{2}{{p}_{\rm P}}}{4\left( \dfrac{1}{{{\phi }_{3}}}-0.5 \right)\gamma \Delta {{p}_{\rm c}}}\dfrac{{{v}_{\rm P}}}{{{v}_{\rm c\Gamma }}}-1 $ | (67) |
气体比容可用真实气体状态方程进行计算。计算喷射器出口处气体比容时,混合介质温度可根据热平衡方程求得
| $ {T_{\rm{c}}} = \dfrac{{{T_{\rm{P}}}{c_{{{\rm{p}}_{\rm{P}}}}} + {T_{\rm{H}}}u{c_{{{\rm{p}}_{\rm{H}}}}}}}{{{c_{{{\rm{p}}_{\rm{P}}}}} + u{c_{{{\rm{p}}_{\rm{H}}}}}}} $ | (68) |
式中:
求解式(68)时,如果喷射器的喷射系数是未知量,可以先给定初值从而确定混合介质温度初值,通过迭代直到满足精度要求,所得结果即为所需的混合介质温度。
3 计算结果对比分析为了验证不同工作气体压力下重新推导的基于真实气体的修正方法和索科洛夫设计方法的差异,以设计空气引射水的喷射器为例,给定喷射器的出口压力0.6 MPa,压缩比取1.5,在1~15 MPa内给定工作气体一系列设计压力,计算该压力范围内所对应的喷射系数值,计算结果如图 2所示。
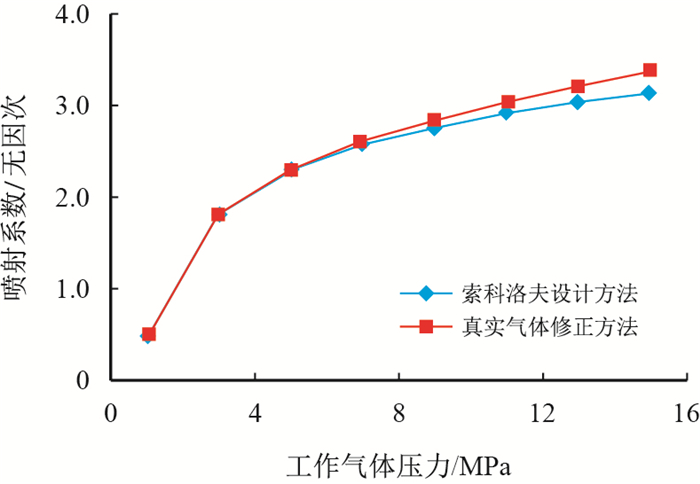 |
| 图2 压缩比为1.5时工作气体压力与喷射系数关系 Fig. 2 Relationship of working gas pressure with ejecting coefficient at compression ratio 1.5 |
从索科洛夫设计方法和真实气体修正方法所得的喷射系数与工作气体压力的关系曲线(图 2)可见,当工作气体压力不大于5 MPa时,基于真实气体的修正方法与索科洛设计方法所得喷射系数结果非常吻合,说明本文推导结果是准确的;但是在压力超过5 MPa后,基于真实气体的修正方法与索科洛夫设计方法所得喷射系数结果差异开始明显,导致差异的主要原因在于,高压条件下气体
为进一步说明情况,对工作气体在1~15 MPa范围内所对应的最佳面积比值进行了计算,计算结果如图 3所示。
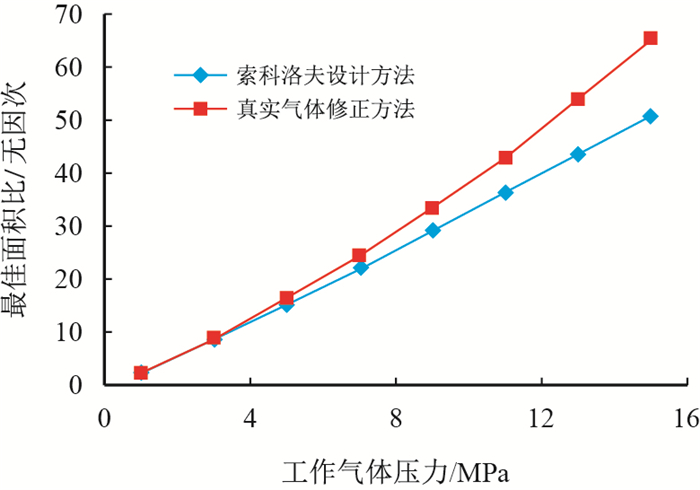 |
| 图3 压缩比为1.5时工作气体压力与最佳面积比关系 Fig. 3 Relationship of working gas pressure with optimum area ratio at compression ratio 1.5 |
计算结果表明,在工作气体压力不大于5 MPa工况下,基于真实气体修正方法最佳面积比结果与索科洛设计方法结果吻合,再次验证了本文推导结果的准确性;但是在压力超过5 MPa后,基于真实气体修正方法与索科洛夫设计方法最佳面积比结果差异随着压力的升高逐渐变大,从另一个角度印证了压力工况对设计结果有显著的影响,再次说明了基于真实气体修正的必要性。
4 结论(1) 从真实气体角度出发,采用气体热力学方法,根据焓和定压比热容的定义,引入真实气体等熵温度绝热指数和等熵容积绝热指数,结合能量方程并运用热力学函数偏微商推证法,推导出真实气体的相对温度、相对压力、相对密度和临界速度等气体动力学函数理论式。
(2) 以真实气体的气体动力学函数理论式为基础,依据动量守恒和质量守恒定律,重点针对小压缩比喷射器的气体动力函数法进行修正,推导出了基于真实气体的气体喷射器与气力输送喷射器的特性曲线、最佳面积比和喷射系数等基本方程,构建了真实气体修正方法。
(3) 低压工况下,基于真实气体的修正方法与索科洛夫设计方法计算结果吻合,说明修正的设计方法覆盖了索科洛夫设计方法;但在高压工况下,两种设计设计方法的结果差异明显,基于真实气体的修正弥补了索科洛夫设计方法的局限,可适用于从低压到高压全压范围的喷射器设计。
| [1] |
DEBERNE N, LEONE J F, DUQUE A, et al. A model for calculation of steam injector performance[J]. International Journal of Multiphase Flow, 1999, 25(5): 841-855. doi: 10.1016/S03019322(98)000718 |
| [2] |
贺遵义. 气体射流泵举升工艺及应用[J]. 钻采工艺, 2000, 23(3): 47-50. HE Zunyi. Lift technology of gas jet pump and it's application[J]. Drilling & Production Technology, 2000, 23(3): 47-50. doi: 10.3969/j.issn.1006-768X.2000.03.011 |
| [3] |
陆宏圻. 喷射技术理论及应用[M]. 武汉: 武汉大学出版, 2004. LU Hongqi. Theories and application of ejector technology[M]. Wuhan: Wuhan University Press, 2004. |
| [4] |
姚志良, 李明忠, 张树华, 等. 蒸汽喷射泵举升稠油参数设计[J]. 中国石油大学学报(自然科学版), 2008, 32(6): 96-100. YAO Zhiliang, LI Mingzhong, ZHANG Shuhua, et al. Parameter design for lifting heavy oil by steam jet pump[J]. Journal of China University of Petroleum (Science & Technology Edition), 2008, 32(6): 96-100. doi: 10.3321/j.issn:1673-5005.2008.06.020 |
| [5] |
陆宏圻, 陆东宏. 喷射技术研究及其发展空间展望[J]. 前沿科学, 2011, 5(3): 32-39. LU Hongqi, LU Donghong. Strive to explore the scientific and technological knowledge, broaden the injection technology development[J]. Frontier Science, 2011, 5(3): 32-39. doi: 10.3969/j.issn.1673-8128.2011.03.006 |
| [6] |
刘效洲. 低压引射式煤粉喷射器的设计[J]. 流体机械, 2012, 40(9): 39-42. LIU Xiaozhou. Innovative design of low-pressure jetcoal powder ejector[J]. Fluid Machinery, 2012, 40(9): 39-42. doi: 10.3969/j.issn.1005-0329.2012.09.009 |
| [7] |
刘双全, 汪雄雄, 樊莲莲, 等. 靖边气田喷射器和压缩机组合增压新工艺[J]. 天然气工业, 2013, 33(5): 96-99. LIU Shuangquan, WANG Xiongxiong, FAN Lianlian, et al. A new technique of supercharging by ejectors and compressors in the Jingbian Gas Field, Ordos Basin[J]. Natural Gas Industry, 2013, 33(5): 96-99. doi: 10.3787/j.issn.1000-0976.2013.05.018 |
| [8] |
戴征书, 陈光明, 张华, 等. 喷射器极限工况特性实验研究[J]. 制冷学报, 2017, 38(5): 114-118. DAI Zhengshu, CHEN Guangming, ZHANG Hua, et al. Experimental study on ejector performance underlimiting operating condition[J]. Journal of Refrigeration, 2017, 38(5): 114-118. doi: 10.3969/j.issn.0253-4339.2017.05.114 |
| [9] |
EL-DESSOUKY H, ETTOUNEY H, ALATIQI I, et al. Evaluation of steam jet ejectors[J]. Chemical Engineering & Processing Process Intensification, 2002, 41(6): 551-561. doi: 10.1016/S0255-2701(01)00176-3 |
| [10] |
HOGGARTH M L. The design and performance of highpressure injectors as gas jet boosters[J]. Proceedings of the Institution of Mechanical Engineers, 1970, 185: 755-766. doi: 10.1243/PIME_PROC_19-70_185_089_02 |
| [11] |
MUNDAY J T, BAGSTER D F. A new ejector theory applied to steam jet refrigeration[J]. Industrial & Engineering Chemistry Process Design and Development, 1977, 16(4): 442-449. doi: 10.1021/i260064a003 |
| [12] |
DUTTON J, MIKKELSEN C, ADDY A. A theoretical and experimental investigation of the constant area, supersonic-supersonic ejector[J]. AIAA Journal, 1982, 20(10): 1392-1400. doi: 10.2514/3.51199 |
| [13] |
SUN D W, EAMES I W. Recent developments in the design theories and applications of ejectors[J]. Journal of the Institute of Energy, 1995, 68: 65-79. |
| [14] |
ALY N H, KARAMELDIN A, SHAMLOUL M M. Modelling and simulation of steam jet ejectors[J]. Desalination, 1999, 123(1): 1-8. doi: 10.1016/S0011-9164(99)00053-3 |
| [15] |
HUANG B J, CHANG J M. Empirical correlation for ejector design[J]. International Journal of Refrigeration, 1999, 22(5): 379-388. doi: 10.1016/S0140-7007(9-9)00002-X |
| [16] |
[苏]E Я索科洛夫H M. 喷射器[M]. 津格尔, 黄秋云, 译. 北京: 科学出版社, 1977.
|
| [17] |
韩惠霖. 喷射理论及其应用[M]. 杭州: 浙江大学出版社, 1990. HAN Huilin. Jet theories and its applications[M]. Hangzhou: Zhejiang University Press, 1990. |
| [18] |
王权, 向雄彪. 蒸汽喷射压缩器喷射系数计算方法研究[J]. 太阳能学报, 1997(3): 314-321. WANG Quan, XIANG Xiongbiao. A study of method for calculating jet coefficient of steam jet compressor[J]. Acta Energiae Solaris Sinica, 1997(3): 314-321. |
| [19] |
刘中常, 李维. 亚临界气体喷射器的设计计算[J]. 南京工业大学学报(自然科学版), 2006, 28(5): 84-88. LIU Zhongchang, LI Wei. Design and calculation of subcritical gas ejector[J]. Journal of Nanjing University of Technology (Natural Science Edition), 2006, 28(5): 84-88. doi: 10.3969/j.issn.1671-7627.2006.05.018 |
| [20] |
沈胜强, 张琨. 新型可调式喷射器性能的计算与分析[J]. 热科学与技术, 2007, 6(3): 230-234. SHEN Shengqiang, ZHANG Kun. Study and calculation of performance of adjustable ejector[J]. Journal of Thermal Science and Technology, 2007, 6(3): 230-234. doi: 10.3969/j.issn.1671-8097.2007.03.009 |
| [21] |
吴伟烽, 冯全科, 向清江, 等. 气-液喷射器内两相流流型分析[J]. 核动力工程, 2007, 28(6): 34-38. WU Weifeng, FENG Quanke, XIANG Qingjiang, et al. Analysis of inner flow patterns in gas-liquid ejectors[J]. Nuclear Power Engineering, 2007, 28(6): 34-38. doi: 10.3969/j.issn.0258-0926.2007.06.009 |
| [22] |
李勇明, 江有适, 高瑞民, 等. 天然气喷射压力计算方法与应用分析[J]. 延安大学学报(自然科学版), 2011, 30(4): 31-34. LI Yongming, JIANG Youshi, GAO Ruimin, et al. The calculation of gas ejection pressure and application analysis[J]. Journal of Yanan University (Natural Science Edition), 2011, 30(4): 31-34. doi: 10.3969/j.issn.1004-602X.2011.04.011 |
| [23] |
ROGDAKIS E D, ALEXIS G K. Design and parametric investigation of an ejector in an air-conditioning system[J]. Applied Thermal Engineering, 2000, 20(2): 213-226. doi: 10.1016/S1359-4311(99)00013-7 |
| [24] |
OUZZANE M, AIDOUN Z. Model development andnumerical procedure for detailed ejector analysis anddesign[J]. Applied Thermal Engineering, 2003, 23(1-8): 2337-2351. doi: 10.1016/S1359-4311(03)002084 |
| [25] |
VALLE J G, JABARDO J M, RUIZ F C. A one dimensional model for the determination of an ejector entrainment ratio[J]. International Journal of Refrigeration, 2012, 35(4): 772-784. doi: 10.1016/j.ijrefrig.2-011.11.020 |
| [26] |
王菲, 吕恒林, 冯伟, 等. 压缩/喷射制冷循环中两相喷射器性能[J]. 化工学报, 2012, 63(10): 3094-3100. WANG Fei, LÜ Henglin, FENG Wei, et al. Performance of two-phase ejector in compression/ejection refrigeration cycle[J]. CIESC Journal, 2012, 63(10): 3094-3100. doi: 10.3969/j.issn.0438-1157.2012.10.013 |
| [27] |
陈洪杰, 卢苇, 庄光亮. 基于实际气体的圆柱形混合室喷射器设计及优化方法[J]. 化工学报, 2015, 66(10): 3881-3887. CHEN Hongjie, LU Wei, ZHUANG Guangliang. Method for design and optimization of cylindrical mixing chamber ejector based on real gas properties[J]. CIESC Journal, 2015, 66(10): 3881-3887. doi: 10.1-1949/j.issn.0438-1157.20150150 |
| [28] |
SHI Chaoyin, CHEN Huiqiang, CHEN Weixiong, et al. 1D model to predict ejector performance at critical and subcritical operation in the refrigeration system[J]. Energy Procedia, 2015, 75: 1477-1483. doi: 10.1016/j.egypro.2015.07.271 |
| [29] |
戴征书, 陈光明, 张华. 内部不可逆损失对喷射器性能影响理论分析[J]. 化工学报, 2016, 67(s2): 78-86. DAI Zhengshu, CHEN Guangming, ZHANG Hua. Theoretical analysis on impact of irreversibility on ejector performance[J]. CIESC Journal, 2016, 67(s2): 78-86. doi: 10.11949/j.issn.0438-1157.20161379 |
| [30] |
高建安. 推证热力学函数偏微商的简捷方法[J]. 江西理工大学学报, 1992(4): 353-361. GAO Jian'an. A simplified method of deducing partial derivatives of thermodynamic function[J]. Journal of Jiangxi University of Science and technology, 1992(4): 353-361. doi: 10.13265/j.cnki.jxlgdxxb.1992.04.013 |
| [31] |
苏长荪. 高等工程热力学[M]. 北京: 高等教育出版社, 1987. SU Changsun. Advanced engineering thermodynamics[M]. Beijing: Higher Education Press, 1987. |
| [32] |
刘晖. 实际气体温度绝热指数和容积绝热指数的计算[J]. 石油化工高等学校学报, 2000, 13(4): 42-45. LIU Hui. Calculation of the isentropic temperature change exponent and isentropic volume change exponent of real gase[J]. Journal of Petrochemical Universities, 2000, 13(4): 42-45. doi: 10.3969/j.issn.10-06-396X.2000.04.009 |
 2018, Vol. 40
2018, Vol. 40


