2. “页岩油气富集机理与有效开发”国家重点实验室, 北京 海淀 100083
2. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Haidian, Beijing 100083, China
国外页岩气田初期采用大井距稀疏井的方式开采,近几年开始关注井距优化研究[1-2],一般通过现场小井距试验获得各类监测资料,通过判别井间干扰进行井距适应性评价[3-5]。但对于压裂改造效果决定气井产能的页岩气藏而言,这类评价方法存在一定的问题。如页岩气藏邻井压裂过程中,本井很容易监测到压裂冲击、压力干扰现象[6-7],化学示踪剂监测结果也显示,压裂过程中压裂液很容易沟通邻井,但这并不意味着气井生产过程中将出现井间干扰。目前普遍认为,只有通过后期生产动态跟踪解释才能获取有效的裂缝半长[8-9],而该半长才是页岩气井井距的决定性因素。国内页岩气勘探开发起步较晚,相关领域的研究较少,主要以借鉴国外的开发经验为主,但中国页岩气田地质特征、压裂规模、生产方式与国外相比均存在一定差异,因此需要从压裂改造效果主控因素出发,有针对性地开展页岩气井井距优化工作。
为了从本质上研究压裂改造效果对气井产能的影响,本文从页岩气藏渗流理论出发,建立多段压裂水平井渗流数学模型,形成基于线性流动阶段识别和特征线诊断技术的改造效果评价技术,可以确定裂缝半长、改造物性等参数,并对参数解释过程中的不确定性进行了分析论证。在此基础上进行均匀压裂气井井距优化和影响因素研究。
1 页岩气渗流特征研究页岩气井的产气能力主要受井控储量、有效裂缝面积(和井筒相连的、具有高导流能力、低存储能力的裂缝和基质的接触面积)、储层渗透率等参数的影响,这些也是影响井距的主要因素[10-11]。研究其对页岩气井产能的影响,需要从表征地下渗流的数学模型入手。
1.1 压裂水平井渗流数学模型目前常用的压裂水平井渗流模型为Bello & Wattenberg及Brown模型[12-13],均认为气井生产时地层中将存在长时期的线性流动,且这一点在国内外页岩气藏均得到验证。对于页岩气藏,为了刻画气体解吸作用,需要在常规模型的基础上重新定义基质系统总压缩系数
| $ c_{\text{tm}} = c_{\text{gm}} + c_{\text{ads}} $ | (1) |
式中:
| $ c_{\text{ads}} = \dfrac{\rho_{\text{sc}}}{\rho_{\text{m}} \phi_{\text{m}}} \dfrac{V_{\text{L}}p_{L}}{\left (p_{\text{L}} + p_{\text{m}} \right)^{2}} $ | (2) |
式中:
下标:m—基质系统;t—考虑吸附气解吸影响后综合值;g—气体;sc—标准状况。
结合该定义对Brown[14-16]模型进行修正,便可建立页岩气藏渗流数学模型。Brown模型,即三线性流模型,将人工裂缝区域、SRV区域及未压裂区域内的流动均看成是线性流动,得到气井定产量生产时拉氏空间内的无因次井底压力解
| $ \begin{array}{ll} \bar\psi_{\text{wfD}} &= \bar\psi_{\text{FD}} \left (x_{\text{D}} = 0\right ) \\ &= \dfrac{\pi}{F_{\text{CD}}u\sqrt{f_{\text{F}} \left (u\right )}} \dfrac{1}{\tanh\sqrt{f_{\text{F}} \left (u\right )}} + \dfrac{S_{\text{c}}}{u} \end{array} $ | (3) |
式中:
| $ {F_1}\left( u \right) = {\omega _1}u + \dfrac{{{\lambda _1}}}{5}\left[ {\sqrt {\dfrac{{15\left( {1 - {\omega _1}} \right)}}{{{\lambda _1}}}{\alpha _{1{\rm{m}}}}u} \coth\left( {\sqrt {\dfrac{{15\left( {1 - {\omega _1}} \right)}}{{{\lambda _1}}}{\alpha _{1{\rm{m}}}}u} } \right) - 1} \right],\\ S_{2} = \tan{\text{h}} \left [\sqrt{F_{2} \left (u\right )} \left (x_{\text{eD}} - 1\right )\right]\sqrt{F_{2} \left (u\right )},\\ {F_2}\left( u \right) = {\omega _2}{\eta _{12}}u + \dfrac{{{\lambda _2}}}{5}\left[ {\sqrt {\dfrac{{15\left( {1 - {\omega _2}} \right)}}{{{\lambda _2}}}{\alpha _{2{\rm{m}}}}{\eta _{12}}u} \\ \coth\left( {\sqrt {\dfrac{{15\left( {1 - {\omega _2}} \right)}}{{{\lambda _2}}}{\alpha _{2{\rm{m}}}}{\eta _{12}}u} } \right) - 1} \right]。$ |
所使用的无因次参数定义为
式中:
下标:i—原始状态;D—无因次;f—裂缝系统;F—人工裂缝系统;1—SRV区;2—未改造区;wf—井底位置处;elf—线性流结束,e—有效裂缝。
对于定井底压力生产的气井,其产量解为
| $ \bar q_{\text{D}} = \dfrac{1}{u^{2} \bar\psi_{\text{wfD}}} $ | (4) |
利用数值反演技术[17]可得到真实空间中的压力和产量解,二者分别用于压力动态分析和产量递减分析,双对数坐标中绘制两种类型的曲线,如图 1所示。
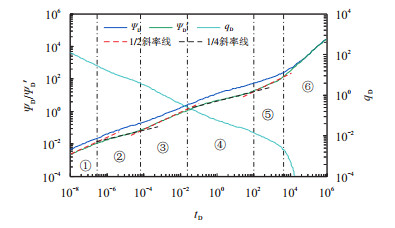 |
| 图1 压裂水平井压力动态曲线及产量递减曲线 Fig. 1 Pressure dynamic and production decline curve |
从图 1可以看出,页岩气多段压裂水平井生产时地层中可能存在6个流动阶段(忽略井储和表皮),但受井筒存储、多段压裂水平经过裂缝间距较小以及SRV外区渗透率较小等原因,仅能明显观察到SRV线性流等部分流动阶段[18-19],如表 1所示。
| 表1 地层流动阶段及其可识别性 Table 1 The visibility of flow regime in shale gas reservoir |
在双对数坐标中,双线性流(早期、晚期)、线性流(裂缝内、SRV区、外区)、边界控制流动阶段的压力动态曲线斜率分别为1/4、1/2、1。对于产量递减曲线,斜率变为相应的负值,但边界控制流阶段表现为指数递减(而非
对几个易识别的流动阶段(早期双线性流阶段、SRV区线性流和边界控制流阶段)的拟压力或产量解做渐近分析[20-21],得到各个解的近似表达式。
早期双线性流动阶段拟压力的渐近解为
| $ {\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}} = \dfrac{{0.04297{q_{{\rm{sc}}}}T}}{{nh\sqrt {{K_{\rm{F}}}{w_{\rm{F}}}} }}\sqrt[4]{{\dfrac{t}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}{K_{1{\rm{f}}}}}}}} + \dfrac{{12.734 \times {{10}^{ - 3}}{q_{{\rm{sc}}}}T}}{{nh{K_{1{\rm{f}}}}}}{S_{\rm{c}}} $ | (5) |
SRV线性流动阶段拟压力的渐近解为
| $ {\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}} = \dfrac{{0.04282{q_{{\rm{sc}}}}T}}{{nh\sqrt {{K_{1{\rm{f}}}}} {x_{\rm{f}}}}}\sqrt {\dfrac{t}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}} + \dfrac{{0.01333{q_{{\rm{sc}}}}T}}{{nh}}\dfrac{{{x_{\rm{f}}}}}{{{K_{\rm{F}}}{w_{\rm{F}}}}} + \\ \dfrac{{12.734 \times {{10}^{ - 3}}{q_{{\rm{sc}}}}T}}{{nh{K_{1{\rm{f}}}}}}{S_{\rm{c}}} $ | (6) |
当压力波及到两条裂缝之间的阻流边界后线性流动阶段结束,结束时间为
| $ {t_{{\rm{elf}}}} = \dfrac{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}{{3.6{K_{1{\rm{f}}}}}}{\left[ {\dfrac{{{y_{\rm{e}}}}}{{({M_{12}} + 2)}}} \right]^2} $ | (7) |
对于边界控制流动阶段,有
| $ {\psi _{\rm{i}}} - {\psi _{{\rm{wf}}}} = \dfrac{{72 \times {{10}^{{\rm{ - }}3}}{q_{{\rm{sc}}}}T}}{{n{\mu _{\rm{i}}}}}\dfrac{t}{{h\left\{ {\left[ {{{(\phi {c_{\rm{t}}})}_1}{x_{\rm{f}}} + {{(\phi {c_{\rm{t}}})}_2}({x_{\rm{e}}}{\rm{ - }}{x_{\rm{f}}})} \right]{y_{\rm{e}}} + {{(\phi {c_{\rm{t}}})}_{\rm{F}}}{x_{\rm{f}}}{w_{\rm{F}}}} \right\}}}+\\[11pt]{\kern 45pt} \dfrac{{0.01333{q_{{\rm{sc}}}}T}}{{nh}}\dfrac{{{x_{\rm{f}}}}}{{{K_{\rm{F}}}{w_{\rm{F}}}}} + \dfrac{{12.734 \times {{10}^{{\rm{ - }}3}}{q_{{\rm{sc}}}}T}}{{nh{K_{1{\rm{f}}}}}}{S_{\rm{c}}} $ | (8) |
对于变产量生产的情况,可通过叠加原理或物质平衡原理得到对应渐近解[22]。这些渐近解即是页岩气压裂水平井改造参数解释的理论基础。
2 基于线性流分析的压裂改造参数解释 2.1 线性流阶段参数解释方法通过渐近分析发现,在双线性流动阶段,双对数诊断图中的
| $ {K_{\rm{F}}}{w_{\rm{F}}} = \dfrac{{1.846 \times {{10}^{ - 3}}q_{{\rm{sc}}}^2{T^2}}}{{{n^2}m_{{\rm{FIBL}}}^2{h^2}}}\sqrt[4]{{\dfrac{1}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}{K_{1{\rm{f}}}}}}}} $ | (9) |
式中:
在内区地层线性流动阶段,双对数诊断图中
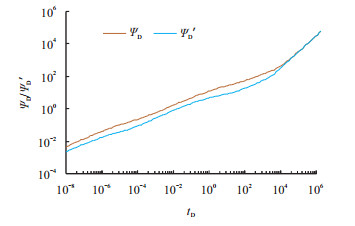 |
| 图2 流动阶段诊断图 Fig. 2 Flow regime diagnostic curve |
提取该阶段的数据,在直角坐标系中做特征线分析(图 3),利用
| $ \sqrt {{K_{1{\rm{f}}}}} {x_{\rm{f}}} = \dfrac{{0.04282{q_{{\rm{sc}}}}T}}{{nh{m_{{\rm{IL}}}}}}\sqrt {\dfrac{1}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}} $ | (10) |
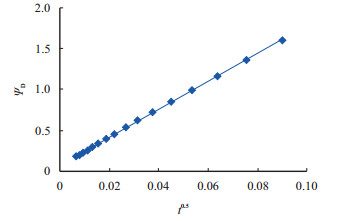 |
| 图3 线性流特征线分析图 Fig. 3 Characteristic curve for linear flow regime |
式中:
从式(6)也可得出直线的截距反映导流能力和汇聚表皮的大小。实际上,该值表征的是井筒附近非达西流、裂缝低导流能力、裂缝和井筒连通性差、裂缝面伤害或者井筒内积液等的综合效应造成的附加压力降,是裂缝质量好坏的笼统响应。
分析线性流动阶段结束时间的表达式,可得
| $ y_{\text{e}} =\left ({M_{12}} + 2\right ) \sqrt{\dfrac{3.6 K_{\text{1f}}t_{\text{elf}}}{\mu_{\rm{i}}\left ( \phi{c_{\text{t}}}\right )_{1}}} $ | (11) |
即利用线性流结束时间,可以求取有效裂缝间距与渗透率的比值。
裂缝半长、储层渗透率及有效裂缝间距(或有效裂缝条数)三者知道了其中之一,便可准确确定另外两个参数。对于致密页岩气藏,短期内只有SRV区内的储量可以动用[23-24],外围储层的供给很少,因此,这3个参数确定后,便可进行井距优化研究。
2.2 改造参数解释的不确定性分析对于多段压裂水平井,有效裂缝条数
| $ {n_{\rm{e}}}\sqrt {{K_{1{\rm{f}}}}} {x_{\rm{f}}} = \dfrac{{0.04282{q_{{\rm{sc}}}}T}}{{h{m_{{\rm{IL}}}}}}\sqrt {\dfrac{1}{{{\mu _{\rm{i}}}{{\left( {\phi {c_{\rm{t}}}} \right)}_1}}}} = {C_1} $ | (12) |
式中:
即总裂缝长度对渗透率平方根的乘积(
当线性流结束时间确定时,有
| $ \dfrac{{{y_{\rm{e}}}}}{{\sqrt {{K_{{\rm{1f}}}}} }} = 2.683\sqrt {\dfrac{{{t_{{\rm{elf}}}}}}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}} $ | (13) |
由于页岩气藏渗透率较低,线性流结束所需要的时间比较长,此时往往取最后一个观测点对应的时间作为线性流的结束时间,意味着线性流虽然目前还未结束,但可能在下一时刻曲线即出现拐点,进入边界控制流动阶段。此时求出的
| $ \dfrac{L}{{{n_{\rm{e}}}\sqrt {{K_{1{\rm{f}}}}} }} = 2.683\sqrt {\dfrac{{{t_{{\rm{elf}}}}}}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}} = {C_2} $ | (14) |
式中:
对比式(13)、式(14),有
| $ {x_{\rm{f}}} = \dfrac{{0.04282{q_{{\rm{sc}}}}T}}{{h{m_{{\rm{IL}}}}}}\sqrt {\dfrac{1}{{{\mu _{\rm{i}}}{{(\phi {c_{\rm{t}}})}_1}}}} = \dfrac{{\left( {{C_1}/{m_{{\rm{IL}}}}} \right)\left( {{C_2}\sqrt {{t_{{\rm{elf}}}}} } \right)}}{L} $ | (15) |
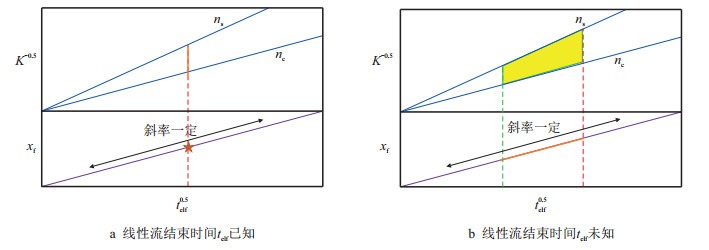
从式(15)得出,一旦线性流阶段直线斜率和拐点(线性流结束时间)确定,裂缝半长就唯一确定,如图 4a。但此时若有效裂缝条数未知,不能唯一确定储层渗透率,只能确定二者的乘积。
 |
|
图4
特征线斜率和线性流结束时间对解释结果的影响
Fig. 4
Influence of characteristic line's slope and |
有效裂缝间距跟有效裂缝条数相关,目前国内外的压裂过程中每一级包含3~4簇裂缝,但微地震监测或示踪剂监测以及产剖测试都显示有些裂缝并不能有效延伸。有效裂缝条数在实际应用中很难唯一确定,但如果每一级裂缝内只有一条裂缝能够有效延伸出去,此时对应的裂缝间距应为有效裂缝间距的最大值,假设每一簇裂缝都能有效延伸,此时对应的裂缝间距为有效裂缝间距的最小值,即裂缝条数的分布范围为(压裂级数
虽然有效裂缝条数在实际生产中难以获取,只要特征线斜率和非稳态线性流结束时间一致,气井可采储量即可确定,裂缝条数判断的准确与否并不影响可采储量的预测结果。
已知裂缝半长以后,便可以压裂改造效果确定的基础上进行井距优化的研究。
3 井距优化实例分析 3.1 模型设计井距的影响因素包括油藏性质、裂缝参数、资本支出、作业费和气价等,应根据气田长期发展策略优化井距[25]。明确压裂改造能力是井距优化的前提,故首先要进行压裂参数解释,再考虑外围补给贡献,综合确定最优井距。设计如表 2参数,建立井距优化渗流数学模型。
| 表2 数值模拟模型参数取值 Table 2 Value of numerical stimulation model |
利用上述数据进行气井产能预测,假设气井初始产量为6
分析发现,生产时间在20~300 d时,该井处于地层线性流动阶段,之后曲线出现拐点,如图 5,表明气井进入边界控制阶段。
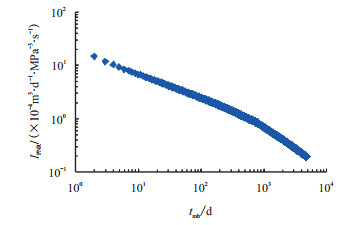 |
| 图5 流动阶段诊断图 Fig. 5 Diagnostic graph of flow regime |
利用特征线分析技术进行压裂改造参数解释(图 6),得到裂缝半长为96.7 m,储层渗透率为1.12
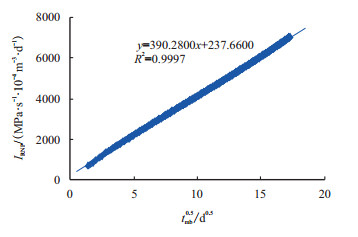 |
| 图6 线性流特征线分析图 Fig. 6 Characteristic line analysis for linear flow |
为了进一步说明压裂改造参数解过程中的不确定性,首先假设气井生产时间较短、裂缝条数也未知,特征线还未出现拐点,在此基础上不断增加气井生产时间,分析随着时间推移压裂改造参数解释的情况,如图 7。
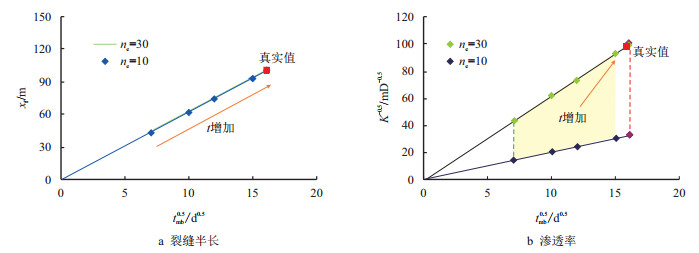 |
| 图7 线性流特征线分析图 Fig. 7 Characteristic line analysis for linear flow |
从图 7可以看出,即便有效裂缝条数难以确定,也并不影响裂缝半长的解释,但相对而言,渗透率解释时多解性较强。随着生产时间的延长,压裂改造参数解空间逐渐缩小,解释结果越来越接近真实值。
进一步分析发现,对于页岩气多段压裂水平井,若井距很小、未改造区物性极差,则未改造区的流动可忽略、模型可简化为双线性流模型。此时,若气井生产动态特征线直线斜率和直线拐点已经确定,即
有了压裂改造参数的解释结果,就可以在此基础上设计对应数值模型模拟气井生产动态,进行井距的优化研究。假设研究区宽度与水平井长度近似如图 8,井距不同,对应着沿区块长度方向上井数不同,当井距为
| $ Q_{\text{a}} = Q \dfrac{L_{0}}{L_{\text{w}}} = L_{0} \dfrac{Q}{L_{\text{w}}} $ | (16) |
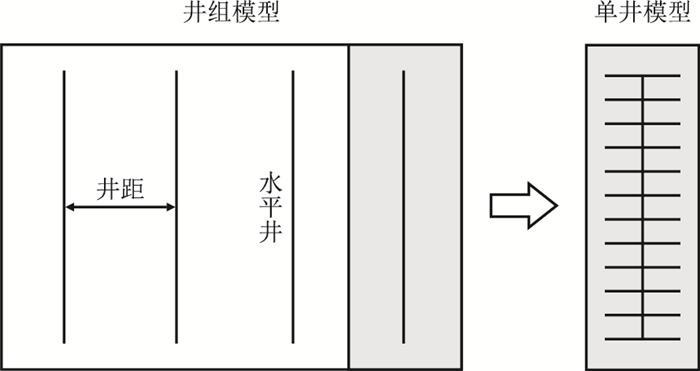 |
| 图8 数值模拟模型示意图 Fig. 8 Diagram of numerical stimulation model |
不同井距下
以上述设计的模型为例,改变SRV外区储层的物性,分析不同外围物性条件下的百米累产,进而得出最优井距,如图 9所示。
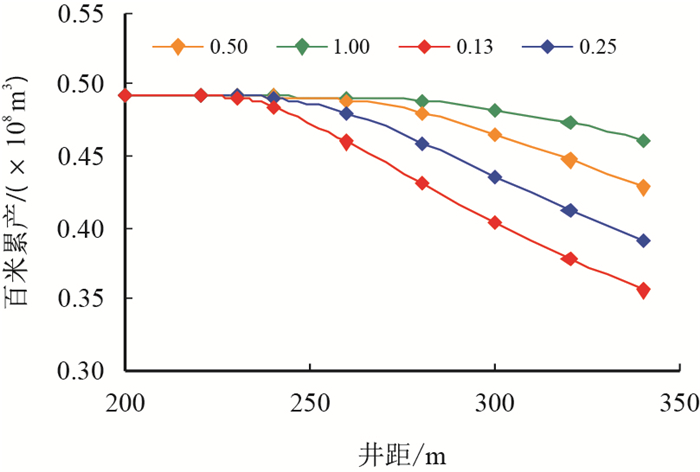 |
| 图9 外区与内区渗透率比值对井距优化结果的影响 Fig. 9 Influence of XRV-SRV permeability ratio on well space |
从图 9可以看出,随着井距的增加,百米累产逐渐降低,当井距比裂缝总长度稍大时,百米累产下降幅度较低,井距增加到一定程度时,百米累产下降速度加快,意味着此时地层采出程度已经明显下降。另外,井距不能过小,当井距小于裂缝长度时,会出现裂缝重叠,造成明显的井间干扰现象(图 10),影响区块的经济开发。因此,图 9中曲线拐点对应的井距即可认为是最优井距。
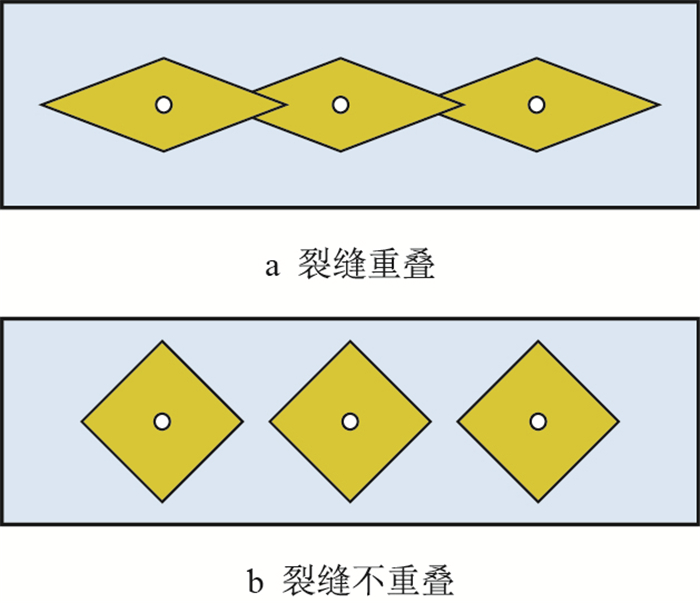 |
| 图10 裂缝半长对井距的影响 Fig. 10 Influence of fracture length well space |
另外,外区物性/内区物性值越大,拐点对应的井距越大,意味着此时外区的补给对气井产量贡献越明显,此时需要放大井距,SRV外区也可以保持较高的采出程度,外区物性越差,井距越接近于裂缝长度。内区物性、导流能力对气井最优井距的影响如图 11、图 12所示。
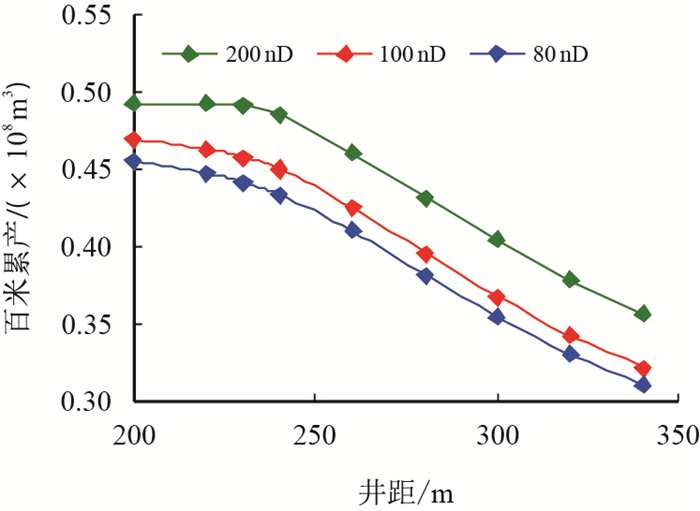 |
| 图11 内区渗透率对井距优化的影响 Fig. 11 Influence of permeability of srv on well space |
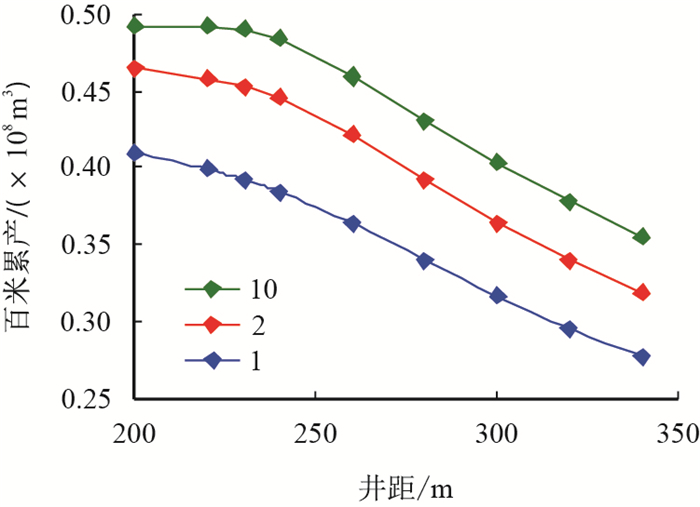 |
| 图12 导流能力对井距优化的影响 Fig. 12 Influence of-fracture conductivityon well space |
从图 11、图 12可以看出,内区物性越差,最优井距越接近与裂缝长度,但当内区物性到达200 nD以上时SRV内区物性对最优井距的影响不再明显,最优井距稍大于裂缝长度。裂缝导流能力的影响与之类似,导流能力越小,最优井距越接近裂缝长度。
4 结论(1) 在修正基质系统等温压缩系数的基础上,利用三线性流模型可以建立针对页岩气藏的压裂水平井渗流数学模型,据此可进行气井压裂改造参数解释。
(2) 页岩气井生产过程中储层存在长时期的线性流,利用特征线分析技术可解释压裂改造参数。参数解释准确程度随着生产时间的延长而增加,当流动进入边界控制流阶段后,即使有效裂缝条数等参数不确定,也能准确确定裂缝半长。
(3) 气井井距的决定性因素是裂缝半长,二者之间的比例关系一定程度上受SRV内外区物性相对大小和裂缝导流能力的影响。
| [1] |
EDWARDS K L, WEISSERT S, JACKSON J B, et al. Marcellus shale hydraulic fracturing and optimal well spacing to maximize recovery and control costs[C]. SPE Hydraulic Fracturing Technology Conference, The Woodlands:2011. doi:10.2118/140463-MS
|
| [2] |
VIRUES C, LYPKIE K, PYECROFT J, et al. Going from conceptual to analytical drilling/completions/reservoir guided model of a cased uncemented multi-fractured horizontal well in the canadian horn river basin[C]. SPE/CSUR Unconventional Resources Conference, Calgary:2015. doi:10.2118/175932-MS
|
| [3] |
刘尧文, 廖如刚, 张远, 等. 涪陵页岩气田井地联合微地震监测气藏实例及认识[J]. 天然气工业, 2016, 36(10): 56-62. LIU Yaowen, LIAO Rugang, ZHANG Yuan, et al. Application of surface-downhole combined microseismic monitoring technology in the Fuling Shale Gas Field and its enlightenment[J]. Natural Gas Industry, 2016, 36(10): 56-62. doi: 10.3787/j.issn.1000-0976.2016.10.007 |
| [4] |
GILDIN E, VALKO P P, FUENTES C G. Analyzing production data from hydraulically fractured wells:The concept of induced permeability field[J]. SPE Reservoir Evaluation & Engineering, 2013, 17(2): 220-232. doi: 10.2118/163843-PA |
| [5] |
WARPINSKI N R, MAYERHOFER M, AGARWAL K, et al. Hydraulic-fracture geomechanics and microseismicsource mechanisms[J]. SPE 158935-PA, 2013. doi: 10.2118/158935-PA |
| [6] |
PORTIS D H, BELLO H, MURRAY M, et al. Searching for the optimal well spacing in the Eagle Ford Shale:Apractical tool-kit[C]. Unconventional Resources Technology Conference, Denver:2013. doi:10.1190/urtec2013-027
|
| [7] |
LIANG Baosheng, DU Meilin, GOLOWAY C, et al. Subsurface well spacing optimization in the Permian Basin[C]. SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin:2017. doi:10.15530/URTEC-2017-2671346
|
| [8] |
YAICH E, SOUZA O C D D, FOSTER R A, et al. A methodology to quantify the impact of well interferenceoptimize well spacing in the Marcellus Shale[C]. SPE/CSUR Unconventional Resources Conference, Calgary:2014. doi:10.2118/171578-MS
|
| [9] |
刘旭礼. 页岩气体积压裂压后试井分析与评价[J]. 天然气工业, 2016, 36(8): 66-72. LIU Xuli. Well test analysis and evaluation after shalegas volume fracturing stimulation[J]. Natural Gas Industry, 2016, 36(8): 66-72. doi: 10.3787/j.issn.1000-0976.2016.08.009 |
| [10] |
贾成业, 贾爱林, 何东博, 等. 页岩气水平井产量影响因素分析[J]. 天然气工业, 2017, 37(4): 80-88. JIA Chengye, JIA Ailin, HE Dongbo, et al. Key factors influencing shale gas horizontal well production[J]. Natural Gas Industry, 2017, 37(4): 80-88. doi: 10.3787/j.issn.1000-0976.2017.04.010 |
| [11] |
于荣泽, 张晓伟, 卞亚南, 等. 页岩气藏流动机理与产能影响因素分析[J]. 天然气工业, 2012, 32(9): 10-15. YU Rongze, ZHANG Xiaowei, BIAN Yanan, et al. Flow mechanism of shale gas reservoirs and influential factors of their productivity[J]. Natural Gas Industry, 2012, 32(9): 10-15. doi: 10.3787/j.issn.1000-0976.2012.09.003 |
| [12] |
BELLO R O, WATTENBARGER R A. Rate transient analysis in naturally fractured shale gas reservoirs[C]. CIPC/SPE Gas Technology Symposium 2008 Joint Conference, Calgary:2008. doi:10.2118/114591-MS
|
| [13] |
BELLO R O, WATTENBARGER R A. Modeling and analysis of shale gas production with a skin effect[J]. Journal of Canadian Petroleum Technology, 2010, 49(12): 37-48. doi: 10.2118/143229-PA |
| [14] |
BROWN M, OZKAN E, RAGAHAVAN R, et al. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2011, 14(6): 663-676. doi: 10.2118/125043-PA |
| [15] |
STALGOROVA K, MATTAR L. Analytical model for unconventional multifractured composite systems[J]. SPE Reservoir Evaluation & Engineering, 2013, 16(3): 246-256. doi: 10.2118/162516-PA |
| [16] |
樊冬艳, 姚军, 孙海, 等. 页岩气藏分段压裂水平井不稳定渗流模型[J]. 中国石油大学学报(自然科学版), 2014, 38(5): 116-123. FAN Dongyan, YAO Jun, SUN Hai., et al. Transient flow model of stage-fractured horizontal wells in shale gas reservoirs[J]. Journal of China University of Petroleum, 2014, 38(5): 116-123. doi: 10.3969/j.issn.1673-5005.2014.05.016 |
| [17] |
VALKÓ P P, ABATE J. Comparison of sequence accelerators for the gaver method of numerical laplace transform inversion[J]. Computers & Mathematics with Applications, 2004, 48(3-4): 629-636. doi: 10.1016/j.camwa.2002.10.017 |
| [18] |
郭小哲, 周长沙. 页岩气储层压裂水平井三线性渗流模型研究[J]. 西南石油大学学报(自然科学版), 2016, 38(2): 86-94. GUO Xiaozhe, ZHOU Changsha. The trilinear seepage model for fractured horizontal well in shale gas reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(2): 86-94. doi: 10.11885/j.issn.1674-5086.2013.10.16.04 |
| [19] |
李凡华, 刘慈群. 有界分形油藏的压力动态分析[J]. 西南石油学院学报, 1997, 19(2): 47-50. LI Fanhua, LIU Ciqun. Pressure transient analysis of finite fractal reservoirs[J]. Journal of Southwest Petroleum Institute, 1997, 19(2): 47-50. doi: 10.3863/j.issn.1000-2634.1997.02.10 |
| [20] |
BROWN M. Analytical trilinear pressure transient model for multiply fractured horizontal wells in tight shale reservoirs[D]. Colorado:Colorado School of Mines, 2009.
|
| [21] |
EL-BANBI A H, WATTENBARGER R A. Analysis of linear flow in gas well production[C]. SPE Gas Technology Symposium, Calgary:1998. doi:10.2118/39972-MS
|
| [22] |
孙贺东. 油气井现代产量递减分析方法及应用[M]. 北京: 石油工业出版社, 2013: 66-74. SUN Hedong. Advanced production decline analysis and application[M]. Beijing: Petroleum Industry Press, 2013: 66-74. |
| [23] |
MAXWELL S S, WALTMAN C, WARPINSKI N R, et al. Imaging seismic deformation induced by hydraulic fracture complexity[J]. SPE Reservoir Evaluation & Engineering, 2009, 12(12): 48-52. doi: 10.2118/102801-PA |
| [24] |
MEDEIROS F, OZKAN E, KAZEMI H. Productivity and drainage area of fractured horizontal wells in tight gas reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2013, 11(5): 902-911. doi: 10.2118/108110-MS |
| [25] |
SAFARI R, LEWIS S, Ma X, et al. Infill-well fracturing optimization in tightly spaced horizontal wells[J]. SPE 178513-PA, 2016. doi: 10.2118/178513-PA |
 2018, Vol. 40
2018, Vol. 40


