2. 中国石油大学(华东)石油工程学院, 山东 青岛 266580
2. School of Petroleum Engineering, China University of Petroleum, Qingdao, Shandong 266580, China
利用空间干扰实现多孔引导裂缝扩展技术已在静态破岩与瓦斯抽采工艺中使用[1-3]。国内外学者多针对建筑物体以及露头岩芯进行研究,建立了裂缝空间导向理论[4-6]。小林秀男研究发现,静力破碎剂破岩时,受孔眼轴心面上应力阴影的相互作用,岩石所受最大拉应力出现在孔眼轴心面处[7]。Liu等在煤层中制造多个导向孔,利用高压水射流对其进行冲击施压,在导向孔周围产生微裂缝情况下再进行压裂,形成了新的引导裂缝[8-9]。针对油井储层,目前主流技术仅限于在井壁进行定向射孔引导人工裂缝扩展。Zhu等研究了定向射孔对水力压裂裂缝的引导作用,构建了预测起裂压力和裂缝扩展形态的数学模型[10]。雷鑫等通过室内实验分析了射孔间距以及地应力对水力裂缝的作用机理[11],认为射孔数的增加以及较小地应力差值更有利于射孔对裂缝的引导。Fallahzadeh等进一步通过物模试验发现井筒以及射孔相互作用,共同制约着致密储层水力裂缝的扩展机制[12]。Chen等通过开展大型水力压裂试验,研究了定向射孔角度以及水平地应力差对裂缝的引导机理[13]。Hong等分析了导向孔数与引导效果的关系,肯定了一定数量导向孔对裂缝的积极引导作用[14]。
径向井是指曲率半径远比常规钻井更小的一种水平井,水平段长度一般为20
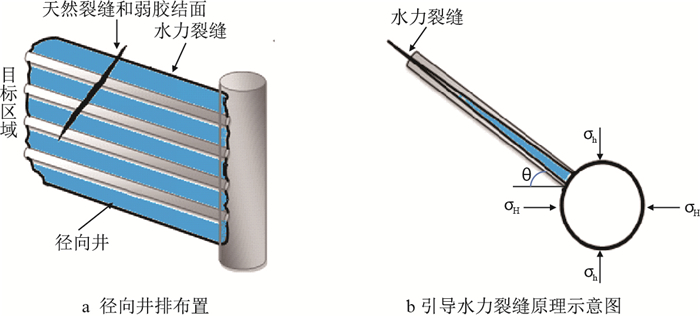 |
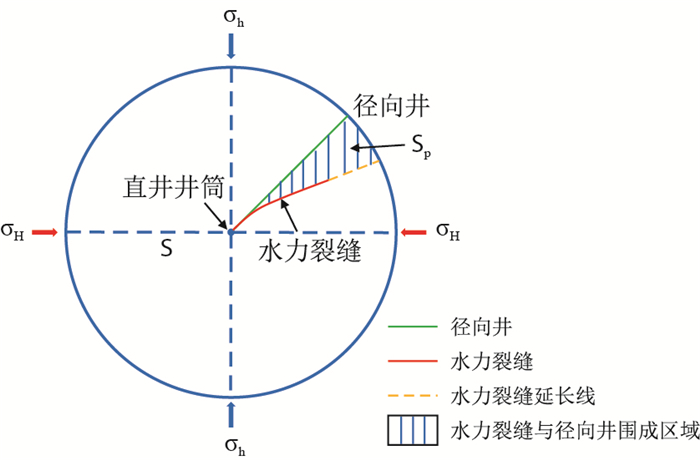
| 图1 径向井排布置及引导水力裂缝原理图 Fig. 1 The schematic diagram of radial wells arrangement and hydraulic fracture propagation |
径向井与射孔的尺寸差别较大,钻井和射孔过程中对地层的影响也不相同,因此,两种方式对水力裂缝的引导机理也有所不同,裂缝扩展路径也存在较大差异。研究清楚径向井排对水力裂缝的引导机理对控制裂缝走向、提高压裂效果有着重大意义。以扩展有限元方法为理论基础,构建了流固耦合数值模型,引入表征裂缝位移向量的函数,选取了裂缝起裂、扩展准则,在ABAQUS有限元平台上进行了演算模拟。揭示了储层应力参数(水平地应力差)、径向井完井参数(径向井排方位角、径向井井径)对水力压裂裂缝的导向规律,为提高径向井储层改造效果提供了一定的理论依据。
1.1 假设条件(1) 垂向上各个径向井平行,形成径向井井排。
(2) 压裂过程中,仅在径向井根部产生一条水力裂缝,且裂缝沿着径向井方位起裂[18-19]。
1.2 模型基本参数数值模拟参数选自胜利油田Z井,模型半径为20 m,油层厚度根据研究需要定为2
|
表1 胜利油田 |
研究过程中通过将扩展函数插入到有限元近似当中,实现对初始裂缝的模拟,表征初始裂缝的位移向量函数见式(1)[20]。
| $ {\mathit{\boldsymbol{{u}}}}=\sum\limits_{I=1}^{N}{{{N}_{I}}(x)\left[ {{\mathit{\boldsymbol{{u}}}}_{I}}+H(x){{\mathit{\boldsymbol{{a}}}}_{I}}+\sum\limits_{m =1}^{4}{{{F}_{m }}(x){\mathit{\boldsymbol{{b}}}}_{I, m }} \right]} $ | (1) |
式中:
最大主应力准则作为判断岩石张性破裂准则,具有稳定性较高、适用性较强的特点,应用于扩展有限元计算方法中,便于收敛,因此,选用最大主应力准则作为判定裂缝起裂依据,最大主应力准则可以表示为[21]
| $ f= \dfrac{\left\langle {{\mathit{\boldsymbol{{σ}}} }_{\max }} \right\rangle }{\mathit{\boldsymbol{{σ}}} _{{\max }{\rm a}}} $ | (2) |
式中:
模型中引入刚度弱化参数
| $ {{t}_{n}}=\left\{ {\begin{array}{*{20}{l}} {(1-D){{T}_{n}}}, & {({{T}_{n}}\geqslant 0)} \\ {{{T}_{n}}}, &{({{T}_{n}}<0)} \end{array}} \right. $ | (3) |
| $ {{t}_{s}}=(1-D){{T}_{s}} $ | (4) |
| $ {{t}_{t}}=(1-D){{T}_{t}} $ | (5) |
式中:
利用ABAUQS前处理模块构建径向井排压裂数值模型,流固耦合机理通过soil模块实现,裂缝起裂扩展利用XFEM方法实现,XFEM方法中需要定义初始裂缝的位移向量函数、岩石破裂准则、岩石损伤演化准则等。数值模拟设计了3组实验,研究径向井排方位角、水平地应力差以及井径对水力裂缝的影响规律,设计方案见表 2。
| 表2 数值模拟研究方案 Table 2 Research program of numerical simulation |
依照表 1参数,建立了两组参数完全一样的数值模型,一组未添加径向井排,另一组在垂向方向组建径向井间距0.5 m,井径0.05 m的3口径向井(图 2)。研究不同径向井排方位角(径向井排方位角指径向井排方向与水平最大地应力方向夹角)对水力裂缝的引导作用。
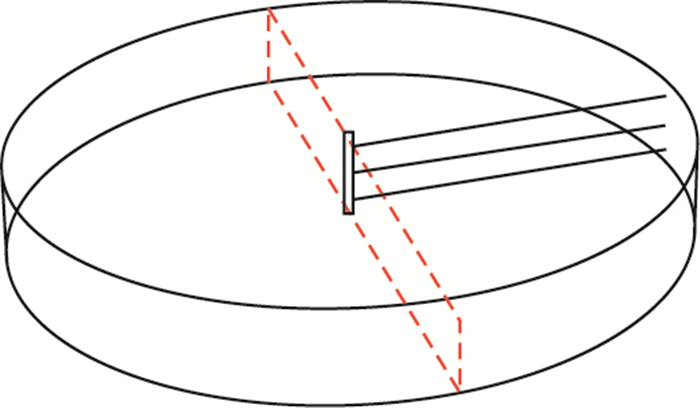 |
| 图2 数值模拟wireframe视图 Fig. 2 The model wireframe view with radial well group |
依照胜利油田Z井基本参数,采用编程和后处理方式实现水力压裂模拟。在模拟时,若不考虑径向井对水力裂缝的作用,则水力裂缝会沿着水平最大地应力方向扩展(图 3);若考虑径向井排对水力裂缝的作用,则水力裂缝扩展路径受径向井排的引导,靠近径向井轴线,且扩展轨迹变得更加曲折。
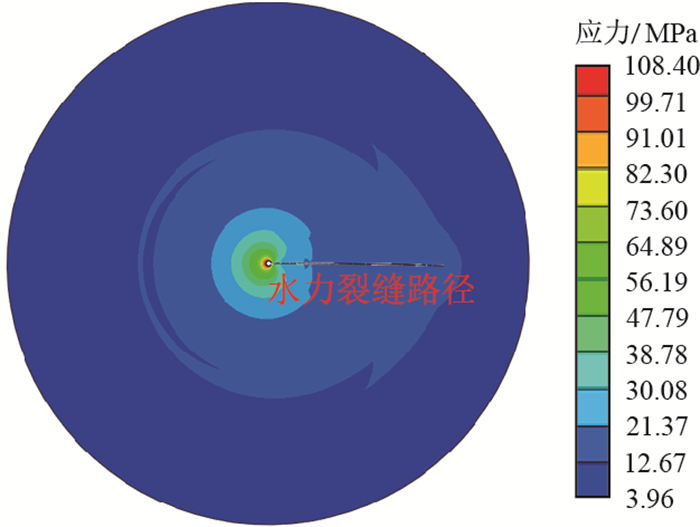 |
| 图3 未受径向井干扰的水力裂缝扩展轨迹 Fig. 3 Fracture propagation without interference from radial well |
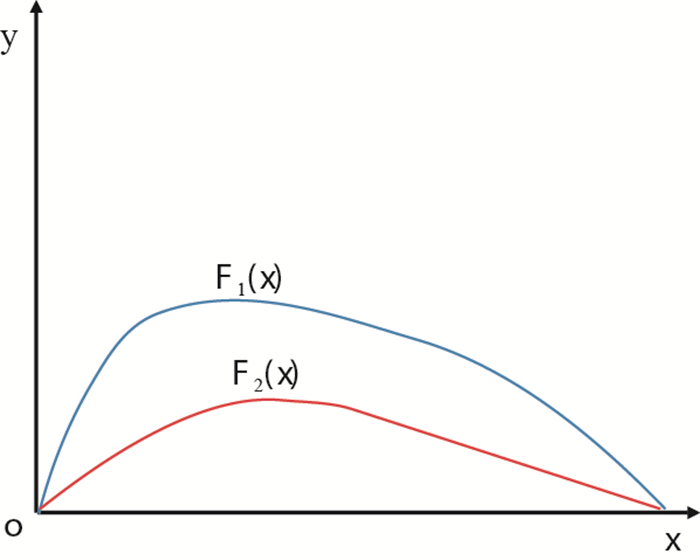
径向井井身参数不同或储层力学参数不同都会对水力裂缝产生不同引导效果,致使裂缝扩展路径发生较大变化。为了从理论上表征径向井排对水力裂缝的引导能力,定义“引导因子
 |
|
图4
引导因子的数学表征
Fig. 4
The mathematical representations of guide factor |
基于以上理论,定义“引导因子”的概念为:二维平面中,径向井井眼轴线与圆形边界以及水力裂缝构成封闭区域的面积
 |
|
图5
引导因子的数学表征
Fig. 5
The mathematical representations of guide factor |
通过大量数值模拟发现,引导因子
| 表3 不同方位角情况下径向井对水力裂缝的引导能力 Table 3 Guiding ability results of radial wells in different azimuth |
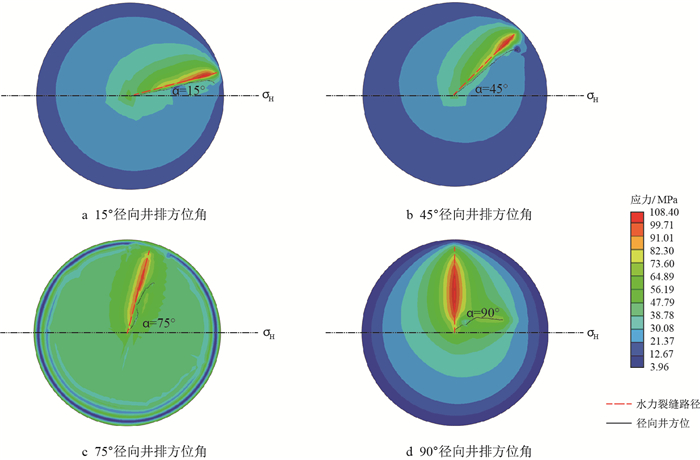
数值模拟结果验证了径向井排对水力裂缝的引导能力,在15°
 |
|
图6
引导因子的数学表征
Fig. 6
The mathematical representations of guide factor |
由图 6可见,径向井排方位角越小,径向井越靠近最大水平主应力方向,引导因子值越小,引导效果越明显。分析认为,径向井排方位角从小变大的过程中,存在一个临界角度,此时径向井对孔眼轴心面上的拉应力与水平最大地应力产生的第一主应力大小相等。当径向井排方位角超过这个临界角度,水力裂缝所需破裂压力增加,且径向井排对孔眼轴心面上的拉应力小于水平最大地应力产生的第一主应力,水力裂缝将会在水平最大地应力的作用下逐步转向,最终沿着水平最大地应力方向扩展。
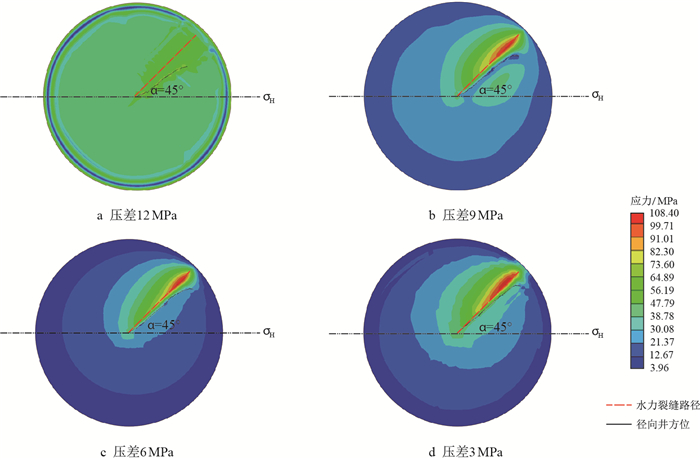
3 水平地应力差对裂缝扩展的影响前人研究过水平地应力差值对定向射孔压裂裂缝的影响机理,针对具有特殊井身参数的径向井排设计了单因素数值模拟试验,以揭示水平地应力差对压裂裂缝的干扰能力。建模过程中,保持径向井井径0.05 m、方位角45°、水平最大地应力41 MPa不变,通过减小水平最小地应力值来实现水平地应力差值变为3,6,9,12 MPa。不同水平地应力差下,径向井排对水力裂缝的引导能力与效果见图 7。
 |
|
图7
引导因子的数学表征
Fig. 7
The mathematical representations of guide factor |
对比水平地应力差值为12 MPa与3 MPa情况下的模拟结果,前者所引导的水力裂缝扩展9.51 m后开始偏转,裂缝偏转角较大,引导因子为0.039,引导作用不明显;后者引导水力裂缝沿井眼方向扩展18.0 m后开始偏转,裂缝偏转角较小,引导因子为0.020,引导距离较远,作用力更强(表 4)。
| 表4 不同水平地应力差值情况下径向井对水力裂缝的引导能力 Table 4 Guiding ability results of radial wells in different pressure difference |
随着水平地应力差值的增加,引导因子值明显逐步变大,反映出径向井排引导水力裂缝的能力减弱,水平地应力差值是影响引导效果的主要因素之一。
随着水平应力差值的增加(水平最小地应力的减小),岩石在最小地应力方向所受压应力减小,即所需破裂压力减小,裂缝的起裂和扩展方向更倾向于最大地应力方向。当岩石所受应力已达到水平最小地应力起裂条件,而未达到孔眼轴心面的破裂条件,岩石将会在水平最小地应力方向张开,逐步向最大主应力方向偏转。
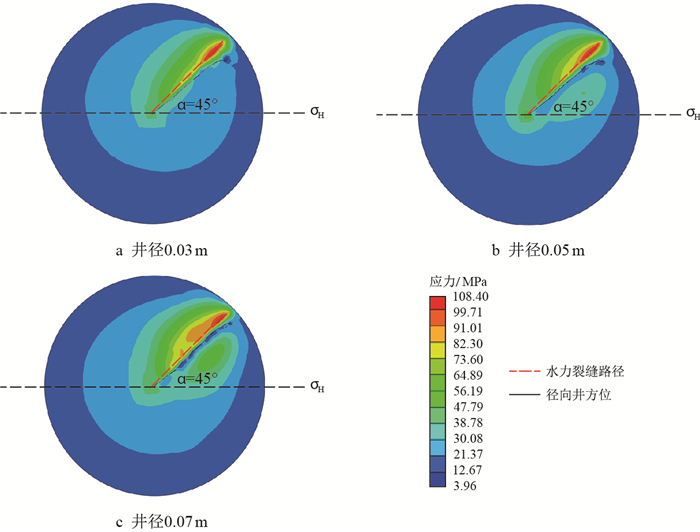
4 井径对裂缝扩展的影响构建了井径为0.03,0.05,0.07 m的径向井排压裂模型,分析井径对水力裂缝的引导效果,模拟结果见图 8。
 |
|
图8
引导因子的数学表征
Fig. 8
The mathematical representations of guide factor |
对比3种井径的压裂结果,0.03 m井径的径向井引导水力裂缝沿井眼轴线扩展14.22 m后开始转向最大主应力方向,裂缝偏转角较大,引导因子为0.024(表 5),引导效果较差;0.05 m井径径向井排引导能力居中;0.07 m井径径向井排引导水力裂缝沿井轴扩展18.5 m发生转向,裂缝偏转角最小,引导因子为0.011,引导效果最佳。随着井径的增加,径向井引导裂缝的能力增强,较大井径有助于提高引导效果,更利于控制裂缝走向。
| 表5 不同井径情况下的引导因子值 Table 5 Guided factor values in different well diameter |
深入分析发现,径向井径会影响水力裂缝的宽度,进而影响后期压裂效果。0.03 m井径的裂缝平均宽度为3 mm,而0.07 m井径的裂缝平均宽度为8 mm,随着径向井井径的增加,水力裂缝的平均宽度逐步增加。大井径径向井排有助于造出宽度更大的裂缝。较大孔径增加了孔壁上压裂液的有效作用面积,使得孔眼周向应力增加,岩石的破裂压力降低,易于产生宽度较宽的水力裂缝,同时也有利于径向井排引导水力裂缝向着有利方向扩展(图 9)。
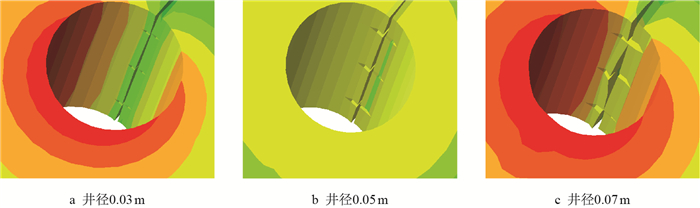 |
| 图9 3种井径下裂缝宽度展示 Fig. 9 Simulation diagram of hydraulic fracture width in three well diameter |
采用大尺寸真三轴水力压裂模拟试验装置对径向井引导水力裂缝的效果进行了验证。水泥试件大小为0.3 m
| 表6 水力压裂试验参数 Table 6 The test parameters of hydraulic fracturing |
两组模拟实验中,试件4实验结果(图 10)显示,当水平地应力差值为3 MPa时,径向井引导效果明显,水力裂缝基本沿着径向井方向扩展。
 |
| 图10 试件4实验结果 Fig. 10 Experimental result of sample 4 |
当水平地应力差值增加为6 MPa时,径向井引导水力裂缝能力减弱,水力裂缝沿着径向井方向扩展7.8 cm后,逐步偏转向最大主应力方向,见图 11。
 |
| 图11 试件5实验结果 Fig. 11 Experimental result of sample 5 |
实验结果与前文所得结论一致。采用扩展有限元方法模拟的水力压裂裂缝扩展规律与实验结果基本吻合,说明径向井对水力裂缝的确可以产生引导作用,同时也验证了数值模拟结果的可靠性。
6 结论(1) 利用一定井间距的径向井排可以引导水力裂缝趋于有利区域,防止地应力干扰而过早发生转向,为径向井水力压裂施工设计提供了理论依据。
(2) 引入“引导因子”,可以对径向井引导水力裂缝的能力及效果进行量化表征:可较精确地反映出径向井排对水力裂缝的引导强度,较小的引导因子反映出径向井更好的引导能力。
(3) 径向井排方位角、水平地应力差、径向井井径会对水力裂缝的引导效果产生影响:较小的径向井排方位角、水平地应力差及较大井径都使径向井排具有较强的引导能力和较好的引导效果,反之亦然。径向井排方位角从15°增加为90°,引导因子增大18.4倍;水平地应力差从3 MPa变为12 MPa,引导因子增大1.97倍;井径从3 cm增加到7 cm,引导因子减小了51.6%。
(4) 较大井径径向井可以诱导产生缝宽值较大的水力裂缝,小井径径向井易于产生缝宽值较小的水力裂缝:0.07 m井距相比0.03 m井距裂缝宽度增加了1.67倍。
(5) 水力压裂模拟实验表明,径向井对水力裂缝可以产生引导作用,验证了数值模拟的可靠性。
| [1] |
张科专. 静态破碎技术在开挖坚硬岩石中的应用[J]. 爆破, 2003, 20(4): 96-97. ZHANG Kezhuan. Application of static fragmentation technique in excavation of hard rocks[J]. Blasting, 2003, 20(4): 96-97. doi: 10.3963/j.issn.1001-487X.2003.04.031 |
| [2] |
姜楠, 徐全军, 龙源, 等. 大孔径静态破碎膨胀压力特性及布孔参数分析[J]. 爆炸与冲击, 2015, 35(4): 467-472. JIANG Nan, XU Quanjun, LONG Yuan, et al. Expansive pressure characteristic and borehole parameter analysis on large scale borehole soundless cracking[J]. Explosion and Shock Waves, 2015, 35(4): 467-472. doi: 10.11883/1001-1455(2015)04-0467-06 |
| [3] |
郝兵元, 李泽华, 黄辉, 等. 静态破碎技术处理高瓦斯矿井巷道悬顶的研究与应用[J]. 爆破, 2015, 32(2): 109-114. HAO Bingyuan, LI Zehua, HUANG Hui, et al. Research and application of static crushing technology handled roadway roof overhang in high-gas coal mine[J]. Blasting, 2015, 32(2): 109-114. doi: 10.3963/j.issn.1001-487X.-2015.02.021 |
| [4] |
BENTLEY P J D, JIANG H, MEGORDEN M. Improving hydraulic fracture geometry by directional drilling in a coal seam gas formation[C]. SPE 167053-MS, 2013. doi: 10.2118/167053-MS
|
| [5] |
鲜保安, 夏柏如, 张义, 等. 开发低煤阶煤层气的新型径向水平井技术[J]. 煤田地质与勘探, 2010, 38(4): 25-29. XIAN Baoan, XIA Bairu, ZHANG Yi, et al. Technical analysis on radial horizontal well for development of coalbed methane of low coal rank[J]. Coal Geology & Exploration, 2010, 38(4): 25-29. doi: 10.3969/j.issn.1001-1986.2010.04.006 |
| [6] |
WU Gang. Process study on radial drilling technology to exploit CBM in Qingshui Basin[J]. China Coal, 2012, 38(1): 9-12. |
| [7] |
小林秀男, 郭润良. 用静力破碎剂破碎岩石时控制岩石断裂面方向研究[J]. 爆破, 1987(2): 72-79. KOBAYASHI Hideo, GUO Runliang. Research on controlling the direction of rock fracture surface when breaking the rock with a static breaking agent[J]. Blasting, 1987(2): 72-79. |
| [8] |
LIU Yong, LIU Xiaotian. Crack-oriented mechanism and method for hydraulic fracturing in coal mine[J]. Disaster Advances, 2013(6): 59-66. |
| [9] |
夏彬伟, 胡科, 卢义玉, 等. 井下煤层水力压裂裂缝导向机理及方法[J]. 重庆大学学报(自然科学版), 2013, 36(9): 8-13. XIA Binwei, HU Ke, LU Yiyu, et al. Mechanism of crackoriented of hydraulic fracture and its technique in mine[J]. Journal of Chongqing University (Natural Science Edition), 2013, 36(9): 8-13. doi: 10.11835/j.issn.1000-582X.-2013.09.002 |
| [10] |
ZHU Haiyan, DENG Jingen, JIN Xiaochun, et al. Hydraulic fracture initiation and propagation from wellbore with oriented perforation[J]. Rock Mechanics and Rock Engineering, 2015, 48(2): 585-601. |
| [11] |
雷鑫, 张士诚, 许国庆, 等. 射孔对致密砂岩气藏水力压裂裂缝起裂与扩展的影响[J]. 东北石油大学学报, 2015, 39(2): 94-101. LEI Xin, ZHANG Shicheng, XU Guoqing, et al. Impact of perforation on hydraulic fracture initiation and extension in tight natural gas reservoirs[J]. Journal of Northeast Petroleum University, 2015, 39(2): 94-101. doi: 10.3969/-j.issn.2095-4107.2015.02.012 |
| [12] |
FALLAHZADEH S H, RASOULI V, SARMADIVALEH M. An investigation of hydraulic fracturing initiation and near-wellbore propagation from perforated boreholes in tight formations[J]. Rock Mechanics and Rock Engineering, 2015, 48(2): 573-584. doi: 10.1007/s00603-014-0595-8 |
| [13] |
CHEN Mian, JIANG H, ZHANG G Q, et al. The experimental investigation of fracture propagation behavior and fracture geometry in hydraulic fracturing through oriented perforations[J]. Petroleum Science and Technology, 2010, 28(13): 1297-1306. doi: 10.1080/10916466.2010.483435 |
| [14] |
HONG J M, SHIN S R, LIM J S, et al. A study on the model for effective hydraulic fracturing by using guide hole[J]. Tunnel & Underground Space, 2014, 24(6): 440-448. |
| [15] |
DICKINSON W, DYKSTRA H, NEES I M, et al. The ultra-short radius radial system applied to thermal recovery of heavy oil[C]. SPE 24087, 1992.
|
| [16] |
吴德元, 沈忠厚. 一种新型高压水力喷射超短半径水平井钻井系统[J]. 石油大学学报, 1994, 18(2): 128-130. WU Deyuan, SHEN Zhonghou. An ultrashort radius radial horizontal drilling system[J]. Journal of The University of Petroleum China, 1994, 18(2): 128-130. |
| [17] |
CAO Y W, XIANG L, MA L Y, et al. Application analysis of vibrating wheel-soil model based on ABAQUS[J]. Advanced Materials Research, 2013, 644: 366-369. doi: 10.4028/www.scientific.net/AMR.644.366 |
| [18] |
张广清, 陈勉, 赵艳波. 新井定向射孔转向压裂裂缝起裂与延伸机理研究[J]. 石油学报, 2008, 29(1): 116-119. ZHANG Guangqing, CHEN Mian, ZHAO Yanbo. Study on initiation and propagation mechanism of fractures in oriented perforation of new wells[J]. Acta Petrolei Sinica, 2008, 29(1): 116-119. doi: 10.3321/j.issn:0253-2697.2008.01.022 |
| [19] |
LI Y H, WANG C J, SHI L H, et al. Application and development of drilling and completion of the ultrashort-radius radial well by high pressure jet flow techniques[C]. SPE 64756-MS, 2000. doi: 10.2118/64756-MS
|
| [20] |
郭历伦, 陈忠富, 罗景润, 等. 扩展有限元方法及应用综述[J]. 力学季刊, 2011, 32(4): 612-625. GUO Lilun, CHEN Zhongfu, LUO Jingrun, et al. A review of the extended finite element method and its applications[J]. Chinese Quarterly of Mechanics, 2011, 32(4): 612-625. |
| [21] |
潘林华, 程礼军, 张士诚, 等. 页岩储层体积压裂裂缝扩展机制研究[J]. 岩土力学, 2015, 36(1): 205-211. PAN Linhua, CHEN Lijun, ZHANG Shicheng, et al. Mechanism of fracture propagation via numerical stimulation of reservoir volume fracture in shale reservoirs[J]. Rock and Soil Mechanics, 2015, 36(1): 205-211. doi: 10.-16285/j.rsm.2015.01.028 |
| [22] |
彪仿俊.水力压裂水平裂缝扩展的数值模拟研究[D].合肥: 中国科学技术大学, 2010. doi: 10.7666/d.-d141088 BIAO Fangjun. A numerical simulation study on hydraulic fracturing of horizontal fractures[D]. Hefei: University of science and technology of China, 2010. doi: 10.7666/d.-d141088 http://cdmd.cnki.com.cn/Article/CDMD-10358-1011124961.htm |
 2018, Vol. 40
2018, Vol. 40


