南海西部海相砂岩油田大多已进入高含水阶段,长期冲刷作用造成储层物性明显变化[1-4},其微观和宏观结构参数随开发生产的持续会发生较大改变,对参数时变规律的研究可用于预测其变化过程,指导油藏工程师重建地质油藏模型,研究油藏剩余油分布,制定针对性开发调整方案,为提高油藏采收率提供科学依据[5-7]。
油藏渗透率的变化是油藏物性变化中最常见的现象之一,对砂岩油田的开发影响较大。目前描述储层渗透率变化规律的表征方法主要包括室内岩芯分析实验和测井参数解释两种方法[8],但均不能定量地表征储层渗透率随水驱冲刷强度的连续变化规律,并且难以与数值模拟相结合[9-10]。在数值模拟中考虑储层参数动态表征方面技术也较为简单:在时间上主要采用分段描述,缺乏连续性;空间上引入动态相渗,主要用于解决生产动态拟合工作,但在剩余油精细刻画及后期预测方面仍存在较大局限性,无法准确表征储层时空变化特征。
本文优选面通量来表征油田累积冲刷强度,通过回归分析,得到面通量和油田生产井试井渗透率的关系,很好地解决了高含水油田渗透率的动态变化规律。
1 油田累积冲刷强度表征油田累积冲刷强度是油田驱替相(水)的累积冲刷强度的分布场,在驱替相冲刷强度研究过程中,其表征经历了多次变化,依次为:单独使用含水饱和度表征、单独使用含水率表征(原始可动水不可表征,开发中后期表征效果差)、综合考虑地质因素与开发因素多指标综合表征(各参数的隶属度和权值的人为因素比较大)、选取过水冲刷倍数表征(反映注入水的储层改造作用,受网格规模大小的影响)到本文的选取面通量表征(图 1)。
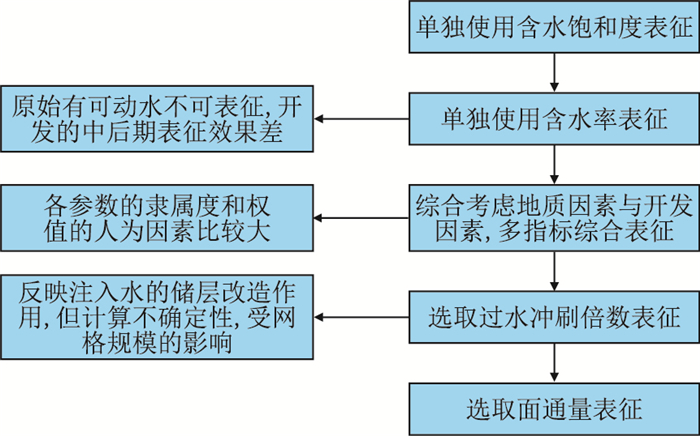 |
| 图1 渗流时变参数定量表征历史 Fig. 1 The history of quantitative characterization of permeability variation |
前人研究[11-12]累积冲刷强度时通常选用过水倍数(或驱替倍数)这个参数,其定义为通过某一区域流体体积的总和与总孔隙体积的比值。用该参数表征存在一定的人为性,受网格尺寸影响较大,在过水倍数相同的情况下,网格尺寸划分越大,过水量越大,冲刷强度越强,网格划分小,则反之。因此用驱替倍数来表征累积冲刷强度只有在网格一致的情况下才有可比性。另外在油藏开发过程中,近井地带的过水量明显大于其他渗流区域,实际过程中,如果网格划分不合理,如网格尺寸划分过小,会导致驱替倍数异常大,结果会出现异常夸张的高冲刷强度区域。
面通量定义为累积通过单位面积的水相体积[13]。用面通量表示累积冲刷强度很好地解决了驱替倍数可比性差的问题,且可以用在数值模拟中动态地表征油藏冲刷强度的强弱,该参数表征油藏冲刷强度较为合理、科学。
| $ M = \dfrac{Q_{\text{w}}}{S} $ | (1) |
式中:
对于给定三维空间上的网格,流体沿三维空间的3个方向流动,流体的流入和流出在3个面上都存在,因此过该网格的总面通量可以用每个方向面通量的和来计算(图 2)。
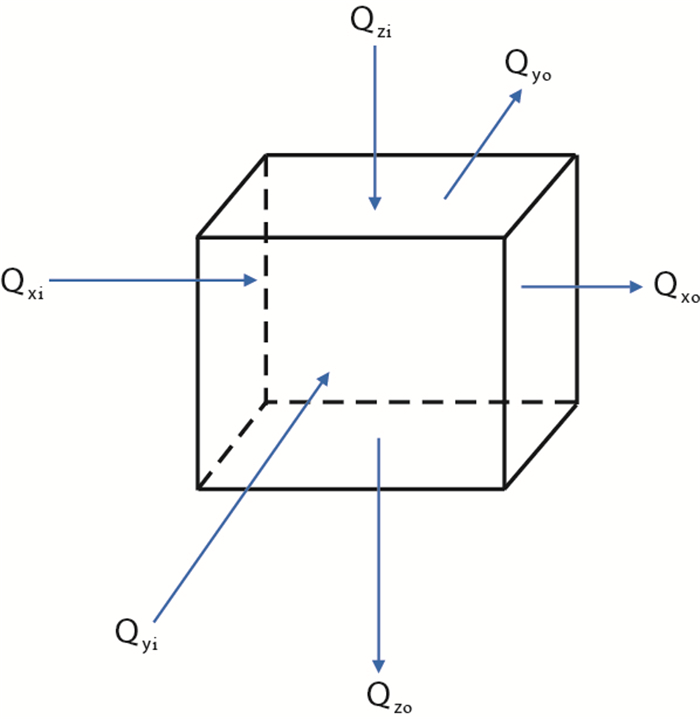 |
| 图2 三维网格各相流动示意图 Fig. 2 Flowing sketch map of three dimensional grid |
总面通量为
| $ M = M_{{x}} + M_{{y}} + M_{{z}} $ | (2) |
| $ M_{{x}} = \dfrac{Q_{x{\rm{o}}}}{S_{{x}}} $ | (3) |
| $ M_{{y}} = \dfrac{Q_{y{\rm{o}}}}{S_{{y}}} $ | (4) |
| $ M_{{z}} = \dfrac{Q_{z{\rm{o}}}}{S_{{z}}} $ | (5) |
式中:
依据W油田各井试井解释波及半径,在数值模拟中圈定相应范围,计算各井试井解释时的面通量,进而用于渗透率变化规律的推导。
2 渗透率变化机理研究储层孔隙空间的喉道半径,岩石岩相,颗粒堆积方式、磨圆、分选、大小分布及胶结程度是影响渗透率变化的重要因素[14-16]。研究表明,在长期水驱过程中,流体与储层不断发生作用,相互作用导致储层微观属性参数不断变化,通过这种持久、强烈、复杂的作用[17-18],微观参数变化不断加剧,最终体现为储层宏观参数(渗透率等)的改变。
储层黏土矿物含量是影响储层孔隙结构及渗透率变化的主要因素,其影响方式可以分为水化膨胀作用和分散迁移作用[19-21]。从大多数油藏开发历程来看,黏土矿物总量随油藏开发的持续有下降趋势:其下降幅度、颗粒迁移比例受储层物性、孔喉直径影响,储层物性越好,孔喉直径越大,其下降幅度及颗粒运移的比例越大,因此造成的储层物性变化幅度也越大,反之,储层物性的变化幅度则较小[22-24]。
经调研及机理研究得到[25]开发过程中储层初始渗透率的改变方向(变好或变差)由储层原始渗透率决定:对于中高渗储层,原始大孔道所占比例较大,水驱冲刷后大孔道发生机械搬运作用,使孔道变得更加通畅,渗透率增大(图 3,调研结果),而低渗储层小孔道所占比例较大,水驱后多发生微粒聚集堵塞孔道,渗透率进一步减小(图 4,调研结果)。除此之外,储层渗透率的变化幅度还与水驱冲刷强度有关,水驱冲刷强度越大,渗透率变化越大,反之,渗透率变化越小[26-28]。
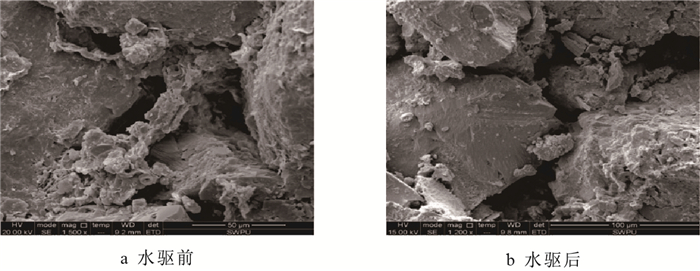 |
| 图3 高渗岩芯水驱前后电镜扫描照片 Fig. 3 Scanning electron microscope of high permeability core before and after water flooding |
 |
| 图4 低渗岩芯水驱前后电镜扫描照片 Fig. 4 Scanning electron microscope of low permeability core before and after water flooding |
南海西部W油田为海相天然水驱砂岩油田,边底水能量充足,目前综合含水达90%左右,进入特高含水阶段。油藏冲刷强度较大,在储层参数变化机理分析的基础上,通过合理的理论推导,描述渗透率的变化规律,实现储层渗透率变化的定量表征。
3.1 W油田各井历年渗透率变化南海西部W油田目前生产层位为ZJ2-1U油组(高渗储层)和ZJ1-1L油组(低渗储层),各油组有多次试井解释(至少两次)井共9口20井次(图 5),本文依据该9口井20井次试井渗透率数据,推导渗透率变化规律预测公式。
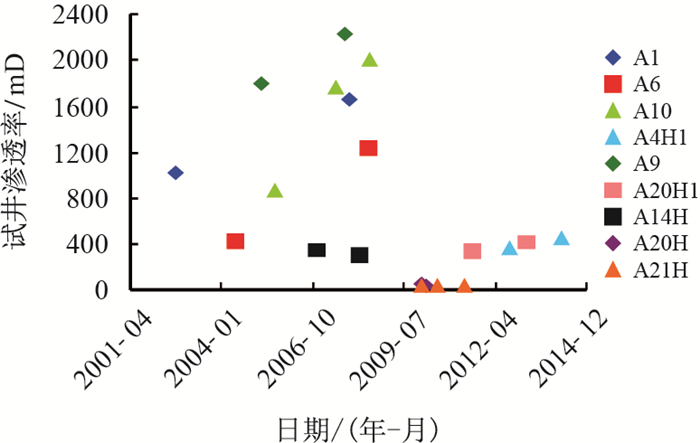 |
| 图5 各井历年试井渗透率结果 Fig. 5 Well test permeability for every years |
从图 5可以看出,水驱后高渗储层(ZJ2-1U油组:A1、A6、A10、A4H1、A9、A20H1,试井渗透率较高)试井渗透率呈增大趋势,低渗储层(ZJ1-1L油组:A14H、A20H、A21H,试井渗透率较低)试井渗透率呈降低趋势。
3.2 渗透率变化规律回归面通量很好地表征了油田高含水期随生产进行油田的冲刷强度,获得渗透率随面通量的变化规律,可以动态预测渗透率的变化,为后期的数值模拟、剩余油分布规律研究提供依据。
为了使关系式有更强的适用性,做渗透率比值随面通量的变化关系(表 1,图 6,图 7),由图 6和图 7可知,渗透率随面通量主要有两种变化趋势:
|
表1 各井渗透率比值( |
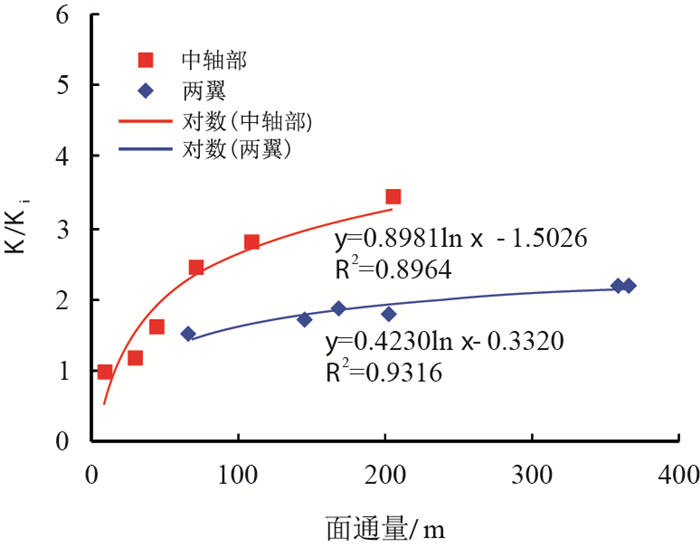 |
| 图6 高渗储层渗透率比值与面通量关系图 Fig. 6 Relationship between permeability ratio and areal flux in medium and high permeability reservoirs |
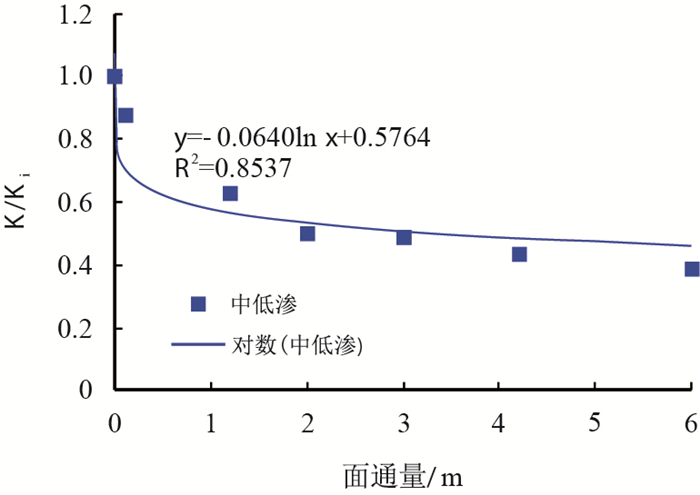 |
| 图7 中低渗储层渗透率比值与面通量关系图 Fig. 7 Relationship between permeability ratio and areal flux in medium and low permeability reservoirs |
第一种:高渗储层(ZJ2-1U油组)渗透率随面通量的增加逐渐增大(表现为渗透率比值
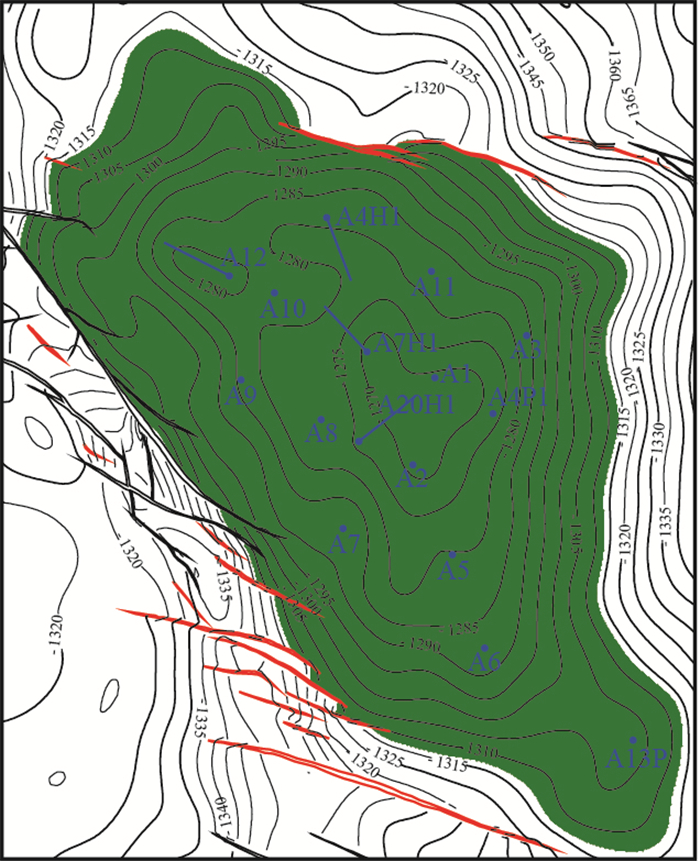 |
| 图8 W油田ZJ2-1U油组含油面积图 Fig. 8 Oil area map of ZJ2–1U oil group in W Oilfield |
第二种:对于中低渗储层(ZJ1-1L油组),渗透率随面通量的增加逐渐减小(表现为渗透率比值
基于以上两种变化规律,推导回归渗透率(渗透率比值:
通过回归分析,发现渗透率比值(
| $ K = K_{\rm{i}} \left(a \ln M + b \right) $ | (6) |
式中:
对于W油田,储层渗透率动态预测公式如表 2所示。
| 表2 W油田不同渗透率储层渗透率随面通量变化定量预测公式 Table 2 Quantitative prediction formula of permeability change of different permeability reservoirs in W Oilfield |
对于部分油田,生产井生产时间较短,过程中没有进行多次压恢测试,没有多次的试井渗透率,进而无法通过对数回归,得到渗透率随面通量的定量预测公式。
通过统计分析W油田各井渗透率随面通量的回归公式,对通式中系数
| 表3 W油田各井对数关系式系数统计表 Table 3 Statistical table of logarithmic relationship of each well in W Oilfield |
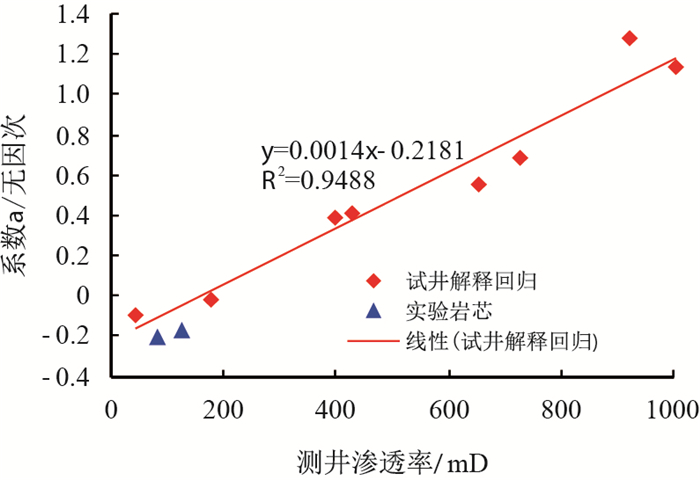 |
| 图9 系数a与测井渗透率关系图 Fig. 9 Relationship diagram of coefficient a and well logging permeability |
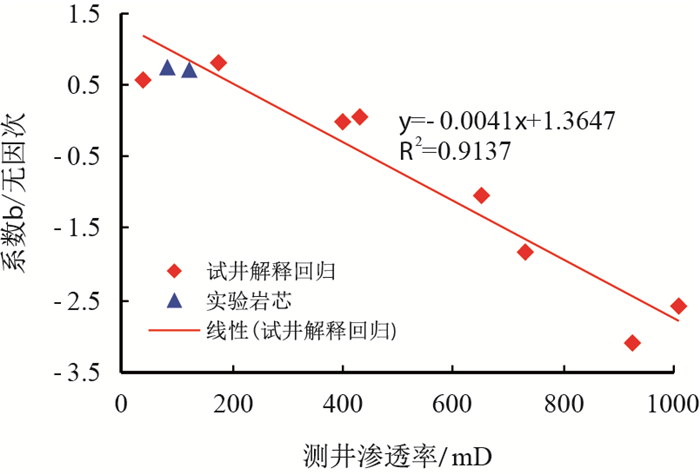 |
| 图10 系数b与测井渗透率关系图 Fig. 10 Relationship diagram of coefficient b and well logging permeability |
从图 9、图 10可以看出,系数
其中,系数
| $ a = 0.0014 K_{\text{c}} -0.2183 $ | (7) |
| $ b =-0.0041 K_{\text{c}}+1.3647 $ | (8) |
式中:
其中,系数
针对以上研究结果,设计两组岩芯,进行高倍驱替,实测岩芯液测渗透率变化,进一步验证渗透率随面通量呈对数关系式的准确性与合理性。
4.1 实验设计本次实验设计两块岩芯(W油田A4P1井岩芯、和露头岩芯各一块)分别进行水驱油高倍驱替实验,记录液测渗透率(残余油下水相渗透率)的变化,进一步验证渗透率随面通量变化的对数关系式。两块岩芯基础数据见表 4所示。
| 表4 实验岩芯基础数据表 Table 4 The data sheet of experimental core |
对两块岩芯做水驱油高倍驱替实验(驱替倍数、面通量见表 5),回归分析渗透率动态变化(
| 表5 两块岩芯实验数据表 Table 5 Two core experiment data sheet |
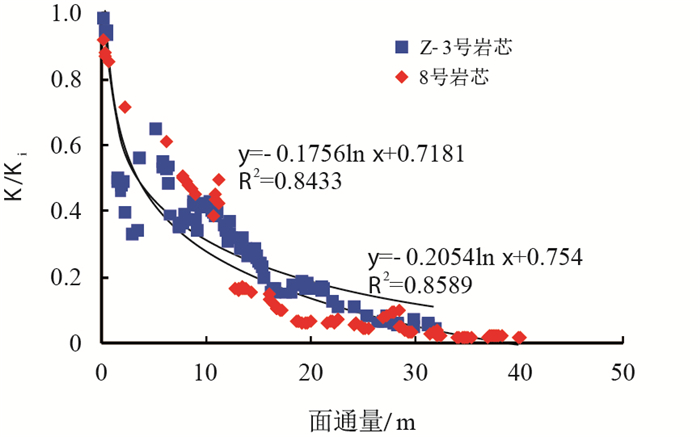 |
| 图11 岩芯液测渗透率与面通量关系式 Fig. 11 Relationship between permeability and areal flux |
两块岩芯实测渗透率与面通量呈对数相关关系,关系式见表 6。
| 表6 两块岩芯渗透率变化规律预测公式 Table 6 Prediction formula of two core permeability variation law |
对实验结果(表 6)的分析,很好地验证了随着开发的进行,油田渗透率随面通量呈对数相关关系变化,该公式可用于油田渗透率动态变化预测。
将表 6中岩芯实验获得的储层渗透率变化规律系数
将W油田渗透率变化规律应用到数值模拟历史拟合中,模型网格数为247
(1) 随着水驱程度的增加,油藏储层渗透率发生趋势性变化,高渗储层与低渗透储层的趋势不同。
(2) 水驱油藏渗透率动态变化规律可以用对数通式
(3) 考虑储层渗透率随水驱过程的变化可提高油田开发中后期对水驱剩余油饱和度分布认识的精度,提高油田挖潜效果。
| [1] |
王志章, 蔡毅, 杨蕾. 开发中后期油藏参数变化规律及变化机理[M]. 北京: 石油工业出版社, 1999: 50-60.
|
| [2] |
刘显太. 中高渗透砂岩油藏储层物性时变数值模拟技术[J]. 油气地质与采收率, 2011, 18(5): 58-62. LIU Xiantai. Study on numerical simulation technology based on time varying physical properties in min-high permeability sandstone reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2011, 18(5): 58-62. doi: 10.3969/j.-issn.1009-9603.2011.05.016 |
| [3] |
郭莉, 王延斌, 刘伟新, 等. 大港油田注水开发过程中油藏参数变化规律分析[J]. 石油实验地质, 2006, 28(1): 85-90. GUO Li, WANG Yanbin, LIU Weixin, et al. Variation law of reservoir parameters during water flooding in Dagang Oilfield[J]. Petroleum Geology & Experiment, 2006, 28(1): 85-90. doi: 10.3969/j.issn.1001-6112.2006.01.017 |
| [4] |
闫育英, 李建荣, 黄仁平. 注水开发对储集层孔隙结构的影响[J]. 油气地质与采收率, 2001, 8(2): 58-60. YAN Yuying, LI Jianrong, HUANG Renping. Effect of water flooding on pore structure of reservoir[J]. Petroleum Geology and Recovery Efficiency, 2001, 8(2): 58-60. doi: 10.3969/j.issn.1009-9603.2001.02.017 |
| [5] |
周守为. 中国近海典型油田开发实践[M]. 北京: 石油工业出版社, 2009: 246-267.
|
| [6] |
何文祥, 许雅. 港东开发区水淹前后储层参数变化规律及机理研究[J]. 断块油气田, 2010, 17(2): 191-193. HE Wenxiang, XU Ya. Law and mechanism of reservoir parameters change both before and after water flooding in Gangdong development Area[J]. Fault-block Oil & Gas Field, 2010, 17(2): 191-193. doi: 10.6056/-dkyqt2012z1002 |
| [7] |
李晓平, 李允, 张烈辉, 等. 水驱强度影响下的油井产量变化规律[J]. 油气井测试, 2004, 13(4): 1-4. LI Xiaoping, LI Yun, ZHANG Liehui, et al. Change rules of oil well production effected by strength of water drive[J]. Well Testing, 2004, 13(4): 1-4. doi: 10.3969/j.-issn.1004-4388.2004.04.001 |
| [8] |
杜玉洪, 张继春, 侯翠芬. 储层宏观物性参数随注水开发动态演化模式研究[J]. 特种油气藏, 2004, 11(5): 52-55. DU Yuhong, ZHANG Jichun, HOU Cuifen. Evolutionary pattern of macroscopic petro physical parameters with water flooding performance[J]. Special Oil and Gas Reservoirs, 2004, 11(5): 52-55. doi: 10.3969/j.issn.1006-6535.-2004.05.016 |
| [9] |
严科, 杨少春, 任怀强. 基于油藏开发动态的储层四维模型的建立[J]. 中国石油大学学报(自然科学版), 2010, 34(1): 12-17. YAN Ke, YANG Shaochun, REN Huaiqiang. Building of 4D reservoir model based on development performance[J]. Journal of China University of Petroleum, 2010, 34(1): 12-17. |
| [10] |
孙焕泉, 孙国, 吴素英, 等. 储集层参数动态地质模型的建立——以胜坨油田二区沙二段12层为例[J]. 石油勘探与开发, 2004, 31(增1): 89-91. SUN Huanquan, SUN Guo, WU Suying, et al. Dynamic geology model establishment of reservoir parameters:Taking 12 layer, Segment 2 of Shahejie Formation, Shengtuo Oilfield, as an example[J]. Petoleum Exploration and Development, 2004, 31(S1): 89-91. doi: 10.3321/j.issn:-1000-0747.2004.z1.021 |
| [11] |
陈付真, 姜汉桥, 李杰, 等. 油藏流场的定量化描述方法及其应用研究[J]. 石油天然气学报, 2011, 33(12): 111-114. CHEN Fuzhen, JIANG Hanqiao, LI Jie, et al. Quantitative liquid descripsion method and its application[J]. Journal of Oil and Gas Technology, 2011, 33(12): 111-114. doi: 10.3969/j.issn.1000-9752.2011.12.023 |
| [12] |
姜瑞忠, 王平, 侯玉培, 等. 基于BP神经网络的油藏流场评价体系研究[J]. 断块油气田, 2012, 19(3): 319-322. JIANG Ruizhong, WANG Ping, HOU Yupei, et al. Study on reservoir flow field evaluation system based on BP neural network[J]. Fault-block Oil & Gas Field, 2012, 19(3): 319-322. doi: 10.6056/dkyqt201203011 |
| [13] |
雷霄, 张乔良, 罗吉会, 等. 涠西南油田群复杂断块油藏水驱剩余油精细表征技术及其现场应用[J]. 中国海上油气, 2015, 27(4): 80-85. LEI Xiao, ZHANG Qiaoliang, LUO Jihui, et al. Fine characterization technique of remaining oif after water flooding for complex fault block reservoirs in southeast Weizhou Oilfield group and its application[J]. China Offshore Oil and Gas, 2015, 27(4): 80-85. doi: 10.11935/j.-issn.1673-1506.2015.04.011 |
| [14] |
李浩, 王香文, 刘双莲. 老油田储层物性参数变化规律研究[J]. 西南石油大学学报(自然科学版), 2009, 31(2): 85-89. LI Hao, WANG Xiangwen, LIU Shuanglian. Variation law of parameters of reservoir physical property in old oilfield[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(2): 85-89. doi: 10.3863/j.issn.1674-5086.2009.02.022 |
| [15] |
刘天鹤, 郭莉, 左毅. 高含水油田注水后油藏参数变化规律研究[J]. 特种油气藏, 2005, 12(2): 42-44, 48. LIU Tianhe, GUO Li, ZUO Yi. Study of reservoir parameter change after water injection in high water-cut oilfield[J]. Special Oil and Gas Reservoirs, 2005, 12(2): 42-44, 48. doi: 10.3969/j.issn.1006-6535.2005.02.013 |
| [16] |
靳文奇, 王小军, 何奉朋, 等. 安塞油田长6油层组长期注水后储层变化特征[J]. 地球科学与环境学报, 2010, 32(3): 239-244. JIN Wenqi, WANG Xiaojun, HE Fengpeng, et al. Characteristics of Chang-6 Oil-bearing formation changes after long term waterflood development in Ansai Oilfield[J]. Journal of Earth Sciences and Environment, 2010, 32(3): 239-244. doi: 10.3969/j.issn.1672-6561.2010.03.004 |
| [17] |
宋万超, 孙焕泉, 孙国, 等. 油藏开发流体动力地质作用——以胜坨油田二区为例[J]. 石油学报, 2002, 23(3): 52-55. SONG Wanchao, SUN Huanquan, SUN Guo, et al. Dynamical geologic process of development liquid:Taking Shengtuo Oilfield as an example[J]. Acta Petrolei Sinica, 2002, 23(3): 52-55. doi: 10.7623/syxb200203011 |
| [18] |
吴素英, 孙国, 程会明, 等. 长期水驱砂岩油藏储层参数变化机理研究[J]. 油气地质与采收率, 2004, 11(2): 9-11. WU Suying, SUN Guo, CHENG Huiming, et al. Study on the reservoir parameters variation mechanism of sandstone oil reservoir with longterm water drive[J]. Petroleum Geology and Recovery Efficiency, 2004, 11(2): 9-11. doi: 10.-3969/j.issn.1009-9603.2004.02.003 |
| [19] |
徐守余, 李红南. 储集层孔喉网络场演化规律和剩余油分布[J]. 石油学报, 2003, 24(4): 48-53. XU Shouyu, LI Hongnan. Evolvement of reservoir porethroat-net and remaining oil distribution[J]. Acta Petrolei Snica, 2003, 24(4): 48-53. doi: 10.7623/syxb200304011 |
| [20] |
王蔚, 鞠斌山, 蒋韧. 疏松砂岩油藏高渗条带识别方法及其应用[J]. 胜利油田职工大学学报, 2006, 20(4): 56-57. WANG Wei, JU Binshan, JIANG Ren. Identification method and application of high permeability strip in unconsolidated sandstone reservoir[J]. Journal of Shengli Oilfield Staff University, 2006, 20(4): 56-57. |
| [21] |
辛治国, 贾俊山, 孙波. 优势流场发育阶段定量确定方法研究[J]. 西南石油大学学报(自然科学版), 2012, 34(2): 119-124. XIN Zhiguo, JIA Junshan, SUN Bo. Research on the quantitative determination of the dominant flow field[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(2): 119-124. doi: 10.3863/j.-issn.1674-5086.2012.02.017 |
| [22] |
朱丽红, 杜庆龙, 李忠江, 等. 高含水期储集层物性和润湿性变化规律研究[J]. 石油勘探与开发, 2004, 31(增1): 8284. ZHU Lihong, DU Qinglong, LI Zhongjiang, et al. Variation of physical characteristics and wettability of reservoir in high water-cut stage[J]. Petroleum Exploration & Development, 2004, 31(S1): 82-84. doi: 10.3321/j.issn:-1000-0747.2004.z1.019 |
| [23] |
王洪光, 蒋明, 张继春, 等. 高含水期油藏储集层物性变化特征模拟研究[J]. 石油学报, 2004, 25(6): 53-58. WANG Hongguang, JIANG Ming, ZHANG Jichun, et al. Simulation on variation of physical properties in high water-cut reservoir[J]. Acta Petrolei Sinica, 2004, 25(6): 53-58. doi: 10.7623/syxb200406011 |
| [24] |
鲍祥生, 尹成, 符志国, 等. 油田注水过程中油藏物性变化规律研究[J]. 西南石油学院学报, 2004, 26(2): 18-22. BAO Xiangsheng, YIN Cheng, FU Zhiguo, et al. Research on the change laws of the oil-pool physical property in the process of the water flooding in the oilfield[J]. Journal of Southwest Petroleum Institute, 2004, 26(2): 18-22. doi: 10.3863/j.issn.1674-5086.2004.02.006 |
| [25] |
邓玉珍, 吴素英, 张广振, 等. 注水开发过程中储层物性特征变化规律研究[J]. 油气采收率技术, 1996, 3(4): 44-52. DENG Yuzhen, WU Suying, ZHANG Guangzhen, et al. Change of reservoir physical properties during development by water flood[J]. Oil & Gas Recovery Technology, 1996, 3(4): 44-52. |
| [26] |
李楠, 李培伦. 砂岩油藏储层渗透率时变实验研究[J]. 内蒙古石油化工, 2015(8): 139-140. LI Nan, LI Peilun. Experimental study on time varying permeability of reservoir permeability in sandstone reservoir[J]. Inner Mongolia Petrochemical Industry, 2015(8): 139-140. doi: 10.3969/j.issn.1006-7981.2015.08.054 |
| [27] |
李阳. 陆相断陷湖盆油藏流场宏观参数变化规律及动态模型[J]. 石油学报, 2005, 26(2): 65-68. LI Yang. Variation rule of macro parameters and dynamic model of oil reservoirs in continental faulted basin[J]. Acta Petrolei Sinica, 2005, 26(2): 65-68. doi: 10.7623/-syxb200502014 |
| [28] |
李存贵, 徐守余. 长期注水开发油藏的孔隙结构变化规律[J]. 石油勘探与开发, 2003, 30(2): 94-96. LI Cungui, XU Shouyu. Law of pore structure variety in reservoir during a long episode waterflooded development[J]. Petroleum Exploration and Development, 2003, 30(2): 94-96. doi: 10.3321/j.issn:1000-0747.2003.02.028 |
 2018, Vol. 40
2018, Vol. 40


