2. 中国石油勘探开发研究院渗流流体力学研究所, 河北 廊坊 065007
2. Research Institute of Petroleum Exploration & Development, Department of Porous Flow & Fluid Mechanics, PetroChina, Langfang, Hebei 065007, China
火山岩气藏勘探开发潜力巨大,开发前景广阔[1-3]。由于特殊的成藏机理,火山岩气藏具有岩相多样、岩性复杂的特征[4-8]。火山岩储集层的岩石中往往发育着无数的裂缝,这些裂缝把岩石分成很多小块,称为基岩块。可以将这种介质分成两类:一类是单纯天然裂缝介质,另一类是裂缝-孔隙型双重介质。大量研究结果表明,火山岩气藏储层渗流普遍存在高速非达西渗流效应、应力敏感效应和滑脱效应[9-12],王强等考虑应力敏感效应建立了火山岩气藏水平井产能计算方法[13-15],但是不同渗流效应对气藏开发的影响尚不明确。为了研究各种效应对气藏开发的影响程度,建立了考虑应力敏感、气体滑脱和高速非线性渗流的裂缝-孔隙型双重介质气藏渗流模型,通过数值模拟分析了应力敏感效应、气体滑脱效应和高速非达西渗流对裂缝-孔隙型双重介质气藏生产的影响,为裂缝-孔隙型双重介质气藏开发提供理论指导。
1 数学模型裂缝-孔隙型双重介质简化物理模型如图 1所示。
 |
| 图1 裂缝-孔隙型双重介质气藏模型 Fig. 1 Fracture-pore dual media model |
裂缝系统
| $ - \nabla \left( {{\rho _{\rm{f}}}{v_{\rm{f}}}} \right) + {q_{\rm{a}}} = \frac{{\partial \left( {{\rho _{\rm{f}}}{\phi _{\rm{f}}}} \right)}}{{\partial t}} $ | (1) |
基岩系统
| $ - \nabla \left( {{\rho _{\rm{m}}}{v_{\rm{m}}}} \right) - {q_{\rm{a}}} = \frac{{\partial \left( {{\rho _{\rm{m}}}{\phi _{\rm{m}}}} \right)}}{{\partial t}} $ | (2) |
式中:ρf, ρm—裂缝系统、基岩系统的气体密度,kg/m3;
νf, νm—裂缝系统、基岩系统中气体的渗流速度,m/s;
qa—标况下裂缝系统与基岩系统之间的窜流量,m3/s;
ϕf, ϕm—裂缝系统、基岩系统的孔隙度,%;
t—时间,s。
1.2 运动方程考虑气体滑脱效应,非达西效应,应力敏感效应,则气体在裂缝和基岩中运动方程分别为
| $ {v_{\rm{f}}} = - {\delta _{{\rm{f1}}}}{\delta _{{\rm{f2}}}}{\delta _{{\rm{f3}}}}\frac{{{K_{\rm{f}}}}}{\mu }\frac{{\partial {p_{\rm{f}}}}}{{\partial x}} $ | (3) |
| $ {v_{\rm{m}}} = - {\delta _{{\rm{m1}}}}{\delta _{{\rm{m2}}}}{\delta _{{\rm{m3}}}}\frac{{{K_{\rm{m}}}}}{\mu }\frac{{\partial {p_{\rm{m}}}}}{{\partial x}} $ | (4) |
式中:Kf, Km—原始地层压力下,不考虑滑脱效应时,线性达西渗流时的裂缝和基岩渗透率,mD;
δf1, δm1—裂缝和基岩渗流的紊流校正系数(高速非达西因子),无因次;
δf2, δm2—裂缝和基岩的应力敏感效应影响因子,无因次;
δf3, δm3—裂缝和基岩的气体渗流滑脱效应影响因子,无因次;
pf, pm—裂缝和基岩处的压力,MPa。
大量的室内实验和现场实践表明,天然气在地层中渗流时,压力梯度和渗流速度满足二项式关系[16]
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{\mu }{K}v + {\delta _1}{\rho _{\rm{g}}}{v^2} $ | (5) |
| $ {\delta _1} = \frac{1}{{1 + \frac{{{\alpha _2}{\rho _{\rm{g}}}Kv}}{\mu }}} $ | (6) |
| $ {\alpha _2} = \frac{{7.644 \times {{10}^{10}}}}{{{K^{1.5}}}} $ | (7) |
式中:p—压力,MPa;
r—半径,m;
μ—黏度,mPa·s;
K—渗透率,D;
v—渗流速度,mm/s;
δ1—紊流校正系数,无因次;
pg—气体密度,kg/m3;
α2—影响惯性阻力的孔隙结构几何特征参数,无因次。
根据实验拟合和文献调研,描述应力敏感介质渗透率与压力的变化函数
| $ {\delta _2} = {{\rm{e}}^{ - {\alpha _{\rm{k}}}\left( {{p_{\rm{i}}} - p} \right)}} $ | (8) |
式中:αK—应力敏感系数,MPa-1;
pi—原始地层压力,MPa。
1941年克林肯贝格给出了考虑气体滑动效应的气测渗透率数学表达式
| $ {K_{\rm{g}}} = {K_{\rm{e}}}(1 + \frac{b}{{\bar p}}) $ | (9) |
式中:Kg—考虑气体滑动效应的气测渗透率数,mD;
Ke—克氏渗透率,mD;
p—平均孔隙压力,MPa;
b—气体滑脱因子,MPa。
1.3 气体状态方程对于实际气体,状态方程为
| $ pV = Zn{\rm{R}}T $ | (10) |
式中:V—气体体积,cm3;
Z—天然气偏差系数,无因次;
n—气体的物质的量,mol;
R—气体常数,R=8.314 J/(K·mol);
T—温度,K。
1.4 窜流方程由于流体在基岩孔隙中流速很小,拟压力表达的窜流方程
| $ {q_{\rm{a}}} = 2\alpha \frac{{{\rho _{\rm{g}}}}}{\mu }\left( {{p_{\rm{m}}} - {p_{\rm{f}}}} \right) $ | (11) |
式中:α—系统的几何形状系数,与基岩的几何形状,裂缝的密集程度有关,无因次。
不同形状的基质岩块形状因子α如表 1所示。
| 表1 典型基质岩块形状因子 Table 1 Shape factor of typical matrix |
将运动方程、状态方程及特征方程代入连续性方程可以得到裂缝和基岩的基本微分方程
| $ \nabla \left( {\frac{{{p_{\rm{f}}}}}{{{Z_{\rm{f}}}}}{\delta _{\rm{f}}}\frac{{{K_{\rm{f}}}}}{{{\mu _{\rm{f}}}}}\nabla {p_{\rm{f}}}} \right) + \frac{{2\alpha {p_{\rm{m}}}}}{{{Z_{\rm{m}}}{\mu _{\rm{m}}}}}\left( {{p_{\rm{m}}} - {p_{\rm{f}}}} \right) = {\phi _{\rm{f}}}\frac{\partial }{{\partial t}}\left( {\frac{{{p_{\rm{f}}}}}{{{Z_{\rm{f}}}}}} \right) $ | (12) |
| $ \begin{array}{l} \nabla \left( {\frac{{{p_{\rm{m}}}}}{{{Z_{\rm{m}}}}}{\delta _{\rm{m}}}\frac{{{K_{\rm{m}}}}}{{{\mu _{\rm{m}}}}}\nabla {p_{\rm{m}}}} \right) + \frac{{2\alpha {p_{\rm{m}}}}}{{{Z_{\rm{m}}}{\mu _{\rm{m}}}}}\left( {{p_{\rm{m}}} - {p_{\rm{f}}}} \right) = \\ \;\;\;\;\;\;\;{\phi _{\rm{m}}}\frac{\partial }{{\partial t}}\left( {\frac{{{p_{\rm{m}}}}}{{{Z_{\rm{m}}}}}} \right) \end{array} $ | (13) |
式中:δf—裂缝中气体渗流滑脱效应、非线性效应、应力敏感效应综合校正因子,δf=δf1δf2δf3,无因次;
δm—基岩中气体渗流滑脱效应、非线性效应、应力敏感效应综合校正因子,δm=δm1δm2δm3,无因次。
Zf,Zm—裂缝和基岩中天然气的偏差系数,无因次;
μf,μm—裂缝和基岩中天然气的黏度,mPa·s。
2 气藏开发影响分析根据克拉美丽气田滴西区块储层温度、压力、边界条件及天然气密度等指标统计分析,数值模拟研究的裂缝-孔隙型双重介质气藏及井筒相关参数如表 2所示。
| 表2 裂缝-孔隙型双重介质气藏基本参数 Table 2 Basic parameters of fracture-pore dual media reservoir |
采用数值模拟分析窜流强度、高速非达西、应力敏感、滑脱效应对裂缝-孔隙型双重介质生产的影响。
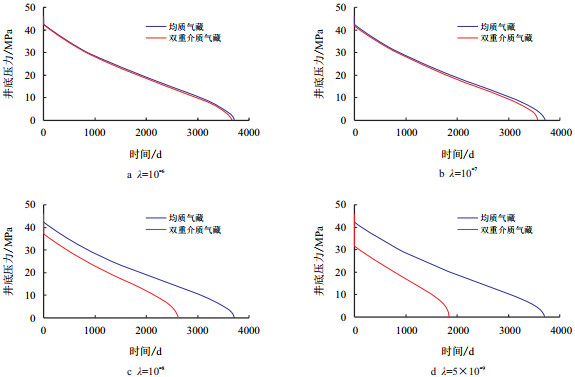
2.1 窜流强度的影响地面以10×104 m3/d定产生产时,模拟窜流系数λ不同时井底压力随时间变化规律,并与相同条件下的等效均质气藏井底压力随时间变化规律进行对比,分析窜流强度(窜流系数λ)对生产的影响。
等效均质气藏的渗透率等于裂缝-孔隙型双重介质气藏渗透率,等效均质气藏的孔隙度等于裂缝-孔隙型双重介质气藏的整体孔隙度(裂缝孔隙度加基岩孔隙度,13%)。实质上,等效均质气藏相当于一个窜流系数λ无限大的裂缝-孔隙型双重介质气藏。
图 2为等效均质气藏和不同窜流系数裂缝-孔隙型双重介质气藏定产生产时井底压力随时间变化关系曲线。
 |
| 图2 均质气藏和双重介质气藏在不同窜流系数时井底压降曲线 Fig. 2 Bottom hole pressure drop curves in homogeneous gas reservoir and double medium gas reservoir with different flow coefficient |
由图 2可见,一般情况下,窜流系数λ达到或大于5×10-9时,定产10×104 m3/d的条件下,生产初期窜流能满足生产要求,而且能够维持较长的稳产期,但在此范围内不同级别的窜流系数λ对双重介质气藏的稳产期影响还是不同的,当窜流系数λ≤10-7时,窜流对稳产期的影响就变得非常显著。
2.2 应力敏感的影响裂缝渗透率变化系数是表征裂缝应力敏感强弱的指标[16],其中,不同裂缝渗透率变化系数对应的裂缝相对渗透率损失如图 3所示。从图 3可以看出,裂缝渗透率变化系数越大,裂缝相对渗透率损失就越严重,尤其当裂缝渗透率变化系数较大、井底及地层压降较大时,因井底及地层压力降引起的裂缝渗透率损失非常大。
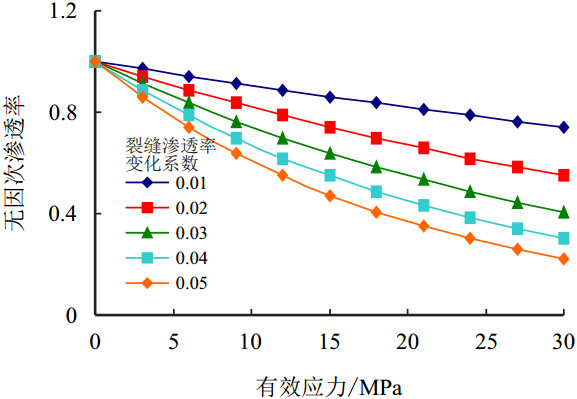 |
| 图3 不同渗透率变化系数下渗透率损失曲线 Fig. 3 Permeability loss curve with different permeability variation coefficient |
数值模拟不同窜流系数、不同裂缝渗透率变化系数下裂缝-孔隙型双重介质气藏以10×104 m3/d定产时井底压力随时间变化规律,数模结果如图 4所示。
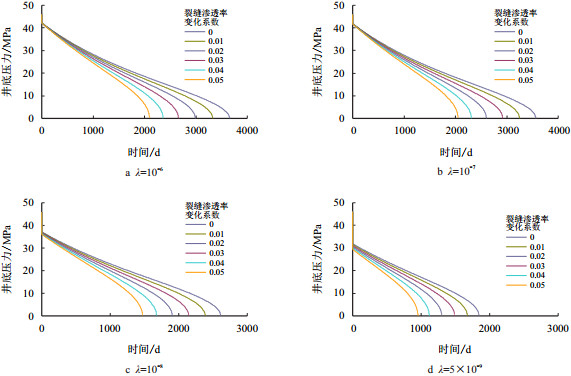 |
| 图4 双重介质气藏在不同窜流系数、不同裂缝渗透率变化系数下的井底压降曲线 Fig. 4 Bottom hole pressure drop curves of double medium gas reservoir under different flow coefficient and permeability coefficient |
生产早期,地层及井底压降小,有效应力增加相对较小,因有效应力增加而造成的储层渗透率损失小,应力敏感效应对井底压降影响也就小;但是持续生产一段时间后,地层及井底压力逐渐下降,有效应力逐渐增加,因有效应力增加而导致的储层渗透率损失也越来越大,应力敏感效应对井底压降影响也越来越大,最终会影响到裂缝-孔隙型双重介质气藏气井的稳产期。
同时也可以发现,基岩系统向裂缝系统窜流能力越弱,即窜流系数λ越小,基岩系统向裂缝系统窜流供气能力也就越弱,裂缝系统压力下降就越快,对应的裂缝系统受到的有效应力增加也就越快,从而导致因有效应力增加造成的储层裂缝渗透损失过早地体现出来,此时,应力敏感性对裂缝-孔隙型双重介质气藏定产生产时的井底压降和稳产期影响愈加显著。
总的来看,当裂缝渗透率变化系数小于0.01时,裂缝渗透率的应力敏感效应对裂缝-孔隙型双重介质气藏生产影响相对较小,可以忽略;而当裂缝渗透率变化系数大于0.02时,裂缝渗透率的应力敏感效应对裂缝-孔隙型双重介质气藏的影响较大,生产时需要考虑。
2.3 高速非达西流的影响数值模拟研究不同窜流系数、不同影响惯性阻力的孔隙结构几何特征参数[17](特征参数越大,气体的非线性渗流越强)下裂缝-孔隙型双重介质气藏10×104 m3/d定产时井底压力随时间变化规律,结果如图 5所示。
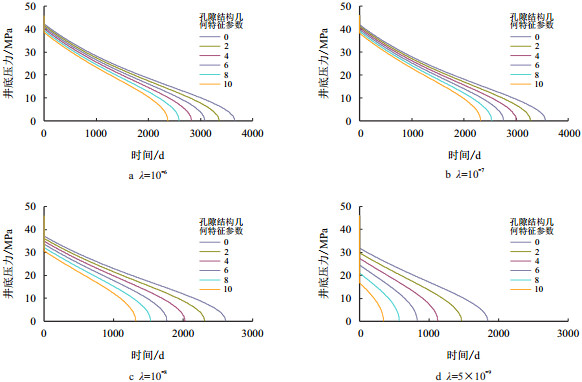 |
| 图5 双重介质气藏在不同窜流系数、不同高速非达西渗流时井底压降对比曲线 Fig. 5 Bottom hole pressure drop curves of double medium gas reservoir with different flow coefficient and non-Darcy flow |
从图 5可以看出,气井开发初期地层及井底压力高,相同质量流量(标准状态下相同体积流量)下气体渗流速度低,非线性渗流效应对井底压降影响并不显著,但是随着生产的继续,井底压力较地层压力继续降低,相同质量流量下气体渗流速度越来越大,非线性渗流效应对井底压降的影响变得越来越显著,气体的非线性渗流最终影响到裂缝-孔隙型双重介质气藏气井的稳产期。
此外还可以发现,基岩系统向裂缝系统窜流能力越弱时,即窜流系数越小,基岩向裂缝窜流的供气能力就越弱,裂缝系统压力下降也就越快,从而导致裂缝系统中气体的渗流速度越来越大,非线性渗流效应对井底压力变化的影响过早显现出来。而且窜流系数越小,相同孔隙结构几何特征参数对应的非线性渗流对井底的压降和稳产期变化规律影响就越大。
2.4 气体滑脱效应的影响数值模拟研究不同窜流系数、不同滑脱系数下裂缝-孔隙型双重介质气藏10×104 m3/d定产时,井底压力随时间变化规律,结果如图 6所示。
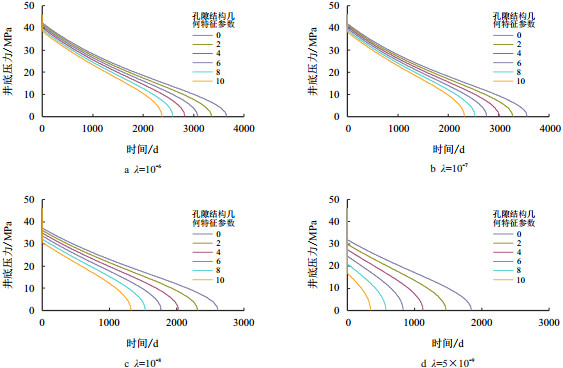 |
| 图6 双重介质气藏在不同窜流系数、不同滑脱系数下井底压降对比曲线 Fig. 6 Comparison curves of bottom hole pressure drop in different media with different flow coefficient and slip coefficient |
图 6表明,气井开发前期井底压力和地层压力都比较高,滑脱效应很弱,气体滑脱对井底压降几乎没有影响。但是随着生产进行到开发后期时,地层及井底压力下降都很大,当井底压力降至10 MPa以下时,滑脱效应开始有所体现,由于气体滑脱效应的存在,导致井底压力下降速度变慢,稳产期增加,而且滑脱系数越大,导致井底的压降速度越慢,相应的稳产期增加越长。但总的来看,相对于其他因素的影响,气体滑脱效应的影响要小得多。
基岩向裂缝窜流能力越弱(窜流系数越小),地层压力下降越快,滑脱效应越早显现出来,滑脱效应对井底压降和稳产期的影响越显著。
3 结论(1) 定产10×104 m3/d时,当窜流系数达到或大于5×10-9时,生产初期窜流就能满足生产要求,而且能够维持较长的稳产期;当窜流系数小于10-7时,窜流对稳产期的影响变得非常显著。
(2) 气井生产早期,应力敏感对井底压降和稳产期的变化规律影响不大;但是在气井生产中后期,由于地层压力明显减小,导致有效应力增加,从而引起储层渗透率损失变大,应力敏感作用增强;窜流系数越小,应力敏感对井底压降的影响越早表现出来,对稳产期的影响也就越大。
(3) 气井生产初期,高速非达西渗流对井底压降影响很小;但是气井生产中后期,储层压力下降显著,气体渗流速度显著增加,高速非达西渗流对井底压降的影响越来越大,最终会影响气井的稳产期;窜流系数越小,高速非达西渗流效应影响越早显现出来,对井底压降和稳产期的影响也就越大。
(4) 地层压力越高,滑脱效应越弱。裂缝-孔隙型双重介质气藏虽然存在气体滑脱效应,但由于储层及井底压力相对较高,因此气体滑脱效应对裂缝-孔隙型双重介质气藏气井生产的影响很小。
| [1] |
彭彩珍, 郭平, 贾闽惠, 等. 火山岩气藏开发现状综述[J].
西南石油学院学报, 2006, 28(5): 69–72.
PENG Caizhen, GUO Ping, JIA Minhui, et al. A Summary of the development present situation for the volcanicrock gas reservoir[J]. Journal of Southwest Petroleum Institute, 2006, 28(5): 69–72. doi: 10.3863/j.issn.1674-5086.-2006.05.019 |
| [2] |
徐正顺, 王渝明, 庞彦明, 等. 大庆徐深气田火山岩气藏的开发[J].
天然气工业, 2008, 28(12): 74–77.
XU Zhengshun, WANG Yuming, PANG Yanming, et al. Development of volcanic rock reservoirs in the Xushen Gas Field in Daqing[J]. Natural Gas Industry, 2008, 28(12): 74–77. doi: 10.3787/j.issn.1000-0976.-2008.12.021 |
| [3] |
曹宝军, 李相方, 姚约东, 等. 火山岩气藏开发难点与对策[J].
天然气工业, 2007, 27(8): 82–84.
CAO Baojun, LI Xiangfang, YAO Yuedong, et al. Challenges and strategies in volcanic gas reservoir development[J]. Natural Gas Industry, 2007, 27(8): 82–84. doi: 10.3321/j.issn:1000-0976.2007.08.025 |
| [4] |
陈树民. 中国东、西部火山岩油气藏运聚成藏机理[J].
天然气工业, 2015, 35(4): 16–24.
CHEN Shumin. Hydrocarbon migration and accumulation mechanism of volcanic reservoirs in eastern and western China[J]. Natural Gas Industry, 2015, 35(4): 16–24. doi: 10.3787/j.issn.1000-0976.2015.04.003 |
| [5] |
覃豪, 李洪娟. 基于岩相的酸性火山岩储层流体识别方法[J].
天然气工业, 2016, 36(4): 35–40.
Qin Hao, Li Hongjuan. A lithofacies-based fluid identification method for acidic volcanic rock reservoirs:Case history of the Xushen Gas Field, Songliao Basin[J]. Natural Gas Industry, 2016, 36(4): 35–40. doi: 10.3787/j.issn.-1000-0976.2016.04.005 |
| [6] |
仇鹏, 孔丽娜, 李道清, 等. 基于体控建模的内幕型火山岩气藏有效储层预测——以准噶尔盆地五彩湾凹陷火山岩气藏为例[J].
天然气工业, 2017, 37(3): 48–55.
QIU Peng, KONG Lina, LI Daoqing, et al. Prediction of net pay zones in volcanic reservoirs with inner structures based on rock-mass controlled modeling:A case study of volcanic gas reservoirs in the Wucaiwan Sag, Junggar Basin[J]. Natural Gas Industry, 2017, 37(3): 48–55. doi: 10.3787/j.issn.1000-0976.2017.03.006 |
| [7] |
孙军昌, 郭和坤, 杨正明, 等. 不同岩性火山岩气藏岩芯核磁孔隙度实验研究[J].
西南石油大学学报(自然科学版), 2011, 33(5): 27–34.
SUN Junchang, GUO Hekun, YANG Zhengming, et al. Experimental study of the NMR porosity of different lithological volcanic rock core samples[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33(5): 27–34. doi: 10.3863/j.issn.1674-5086.2011.05.005 |
| [8] |
杨正明, 郭和坤, 姜汉桥, 等. 火山岩气藏不同岩性核磁共振实验研究[J].
石油学报, 2009, 30(3): 400–408.
YANG Zhengming, GUO Hekun, JIANG Hanqiao, et al. Experimental study on different lithological rock of volcanic gas reservoir using nuclear magnetic resonance technique[J]. Acta Petrolei Sinica, 2009, 30(3): 400–408. doi: 10.3321/j.issn:0253-2697.2009.03.014 |
| [9] |
董家辛, 童敏, 冉博, 等. 火山岩气藏不同储渗模式下的非线性渗流机理[J].
石油勘探与开发, 2013, 40(3): 346–351.
DONG Jiaxin, TONG Min, RAN Bo, et al. Nonlinear percolation mechanisms in different storage-percolation modes in volcanic gas reservoirs[J]. Petroleum Exploration and Development, 2013, 40(3): 346–351. doi: 10.-11698/PED.2013.03.12 |
| [10] |
杨正明, 霍凌静, 张亚蒲, 等. 含水火山岩气藏气体非线性渗流机理研究[J].
天然气地球科学, 2010, 21(3): 371–374.
YANG Zhengming, HUO Lingjing, ZHANG Yapu, et al. Mechanism of non-liner gas seepage flow in waterbearing volcanic gas reservoir[J]. Natural Gas Geoscience, 2010, 21(3): 371–374. doi: 10.11764/j.issn.1672-1926.-2010.03.371 |
| [11] |
章星, 杨胜来, 李芳芳, 等. 火山岩气藏气水两相渗流特征分析[J].
断块油气田, 2013, 20(5): 631–633.
ZHANG Xing, YANG Shenglai, LI Fangfang, et al. Characteristics analysis of gas-water two-phase flow in volcanic gas reservoir[J]. Fault-Block Oil & Gas Field, 2013, 20(5): 631–633. doi: 10.6056/dkyqt201305021 |
| [12] |
许进进, 徐旭辉, 凡哲元, 等. 考虑启动压力梯度下的火山岩气藏数值模拟研究[J].
石油与天然气地质, 2010, 31(2): 240–259.
XU Jinjin, XU Xuhui, FAN Zheyuan, et al. A numerical simulation of volcanic gas reservoirs under consideration of start up pressure gradient[J]. Oil & Gas Gelolgy, 2010, 31(2): 240–259. doi: 10.11743/ogg20100216 |
| [13] |
闫利恒, 王延杰, 麦欣, 等. 克拉美丽气田火山岩气藏配产方法优选[J].
天然气工业, 2012, 32(2): 51–53.
YAN Liheng, WANG Yanjie, MAI XIN, et al. Optimization of production allocation methods for volcanic gas reservoirs in the Kelameili Gas Field[J]. Natural Gas Industry, 2012, 32(2): 51–53. doi: 10.3787/j.issn.1000-0976.2012.-02.011 |
| [14] |
王志平, 冉博, 童敏, 等. 双孔双渗火山岩气藏裸眼压裂水平井产能预测方法[J].
石油勘探与开发, 2014, 41(5): 585–590.
WANG Zhiping, RAN Bo, TONG Min, et al. Forecast of fractured horizontal well productivity in dual permeability layers in volcanic gas reservoirs[J]. Petroleum Exploration and Development, 2014, 41(5): 585–590. doi: 10.11698/PED.2014.05.10 |
| [15] |
王强, 童敏, 武站国, 等. 致密火山岩气藏压裂水平井产能预测方法[J].
西南石油大学学报(自然科学版), 2014, 36(4): 107–115.
WANG Qiang, TONG Min, WU Zhanguo, et al. An unsteady productivity prediction method of multi-fractured horizontal well in tight volcanic rock reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(4): 107–115. doi: 10.11885/j.-issn.1674-5086.2013.11.26.04 |
| [16] |
张建国, 杜殿发, 候健, 等.
油气层渗流力学[M]. 北京: 中国石油大学出版社, 2009: 186-187.
ZHANG Jianguo, DU Dianfa, HOU Jian, et al. Oil and gas seepage mechanics[M]. Beijing: China University of Petroleum Press, 2009: 186-187. |
| [17] |
姜汉桥, 姚军, 姜瑞忠.
油藏工程原理与方法[M]. 北京: 石油大学出版社, 2000: 37-39.
JIANG Hanqiao, YAO Jun, JIANG Ruizhong. Principles and methods of reservoir engineering[M]. Beijing: University of Petroleum Press, 2000: 37-39. |
 2018, Vol. 40
2018, Vol. 40


