2. 中国石油集团测井有限公司华北事业部, 河北 任丘 062552
2. North China Division, China Petroleum Logging Co. Ltd., CNPC, Renqiu, Hebei 062552, China
碎屑岩储层一直以来都是中国东部各油田增储上产的主体产层,但随着勘探的不断深入,面临对象变为储层物性及孔隙结构越来越差的油气藏[1-5],如何利用核磁共振技术更加准确地表征储层孔隙结构特征是问题的关键所在。
利用核磁共振技术表征储层孔隙结构的通常做法是将
在直接利用核磁共振
以冀中地区中深层、中低孔、低渗透砂泥岩储层作为研究对象,开展了以岩石核磁共振实验为基础的储层孔隙结构表征方法研究,经过孔隙结构参数优选构建储层品质指数,结合区域试油测试数据确定储层品质下限,建立了储层品质指数与储层产能的关系,以期解决该地区储层有效性及产能评价的难题。
1 基于核磁共振实验的储层孔隙结构研究针对冀中地区沙河街组沙一段、沙二段,选取了33块砂岩岩样进行饱和样及离心样的核磁共振实验测量,经数据反演得到每一块岩样饱和状态下的
核磁共振
在实际计算时,通过“遍历算法”搜索
核磁共振
双截止值的选取目前主要通过地区岩样压汞资料与核磁共振实验进行刻度来确定,因此
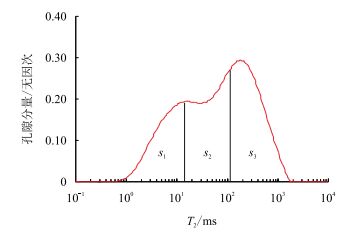
| ${S_1}=\dfrac{{\int_{0.1}^{25} {{\phi _i}\rm{d}\phi } }}{{{\phi _{\rm{nmr}}}}} $ | (1) |
| ${S_2}{\rm{ = }}\dfrac{{\int_{25}^{125} {{\phi _i}\rm{d}\phi } }}{{{\phi _{\rm{nmr}}}}} $ | (2) |
| ${S_3}{\rm{ = }}\dfrac{{\int_{125}^{10000} {{\phi _i}\rm{d}\phi } }}{{{\phi _{\rm{nmr}}}}} $ | (3) |
式中:
核磁共振
| $T_{2, \rm{gm}}={\left( {\prod\limits_{i = 1}^N {{T_{2i}}^{{\phi _i}}} } \right)^{\dfrac{1}{{{\phi _{\rm{nmr}}}}}}} $ | (4) |
式中:
式(3)最初在SDR渗透率计算模型中引入。之后的研究发现,其与压汞参数具有很好的对应关系[18-19],是评价岩石孔隙结构的一个重要参数。
岩石的孔隙结构越好,孔隙中的可动流体所占比例越大,反之亦然。因此,利用岩石束缚水含量的多少可以间接反映其孔隙结构的情况。核磁共振测井是目前唯一可以区分储层中可动流体和束缚流体的测井方法,在确定储层束缚水体积时具有独特优势[20-21]。为此,针对冀中地区岩样的实际情况,采用薄膜水模型计算岩样束缚水饱和度,并对原计算模型进行改进,使得计算结果更精确、更符合该地区实际。
Coates等通过大量实验,提出了利用薄膜水模型(SBVI法)计算束缚水体积的计算模型[22]
| $\begin{equation} \left\{ \begin{array}{l} {V_{{\rm{SB}}}} = \sum\limits_{i = 1}^N {{w_i}{\phi _i}} \\ {w_i} = \dfrac{1}{{m{T_{2, i}} + b}} \end{array} \right. \end{equation}$ | (5) |
式中:
Coates等认为,砂岩储层中
通过该地区的实验研究,本文提出改进的计算模型
| ${w_i} = {{\rm{e}}^{a{T_{2, i}}^b}} $ | (6) |
式中:
图 2、图 3为新旧模型计算结果对比图,从图中可以看出,原模型计算结果的绝对误差为4.60,相对误差为12.66%;而新模型计算结果的绝对误差为3.04,相对误差为7.74%。从结果来看,计算精度有所提高。
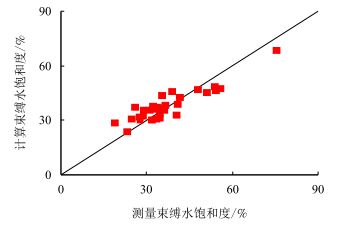 |
| 图2 原模型计算结果对比 Fig. 2 The comparative result of old model |
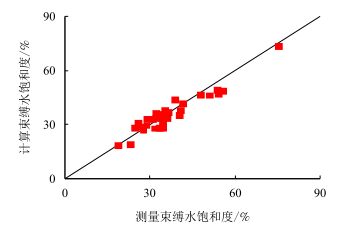 |
| 图3 新模型计算结果对比 Fig. 3 The comparative result of new model |
通过以上分析,利用表征孔隙结构的特征参数峰值、三孔隙分量、几何平均值及束缚水饱和度,构建如下综合评价储层孔隙结构的储层品质指数
| ${I_{{\rm{PS}}}} = \dfrac{{\ln ({T_{{\rm{2, peak}}}} \times {T_{{\rm{2, gm}}}}) \times {S_3}}}{{{S_1} \times {V_{{\rm{SB}}}}}} $ | (7) |
式中:
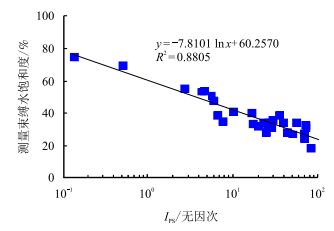
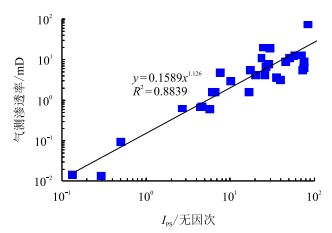
对岩样进行计算分析,结果表明,该综合指数在表征储层品质具有很高的可信度,具体表现为:(1)计算的储层品质指数与实验室测量的渗透率及称重法测量的束缚水饱和度具有很好的相关性(图 4、图 5);(2)储层品质指数能够很好地体现具有相似孔隙度、不同渗透率岩样的差异,即在地层条件下,从相对微观的角度能够反映出孔隙度相似、而产量存在显著差异的储层,如编号为N13与N23的两块岩样,其孔隙度相当,渗透率相差一个数量级,计算的储层品质指数相差近6倍,具体计算结果见表 1。
 |
|
图4
储层品质指数与束缚水饱和度关系
Fig. 4
The relationship between |
 |
|
图5
储层品质指数与渗透率关系
Fig. 5
The relationship between |
| 表1 岩样N13与N23孔隙结构参数对比 Table 1 Comparative result of pore structure parameters about sample No. 13 and No. 23 |
储层的孔隙结构决定着储层的渗流能力,渗透率和可动流体饱和度越大,储层品质越好[23-24],因此,储层品质的好坏直接决定了储层在正常压力下的产液能力。前人在储层品质与储层自然产能的关系方面做过不少研究,万金彬等利用物性参数(孔隙度、渗透率)组合构建储层品质因子来预测储层产能,在南堡油田得到应用[25];苏俊磊等通过核磁共振测井
结合试油测试资料,分析了冀中地区23个试油结论为油层或油水同层(具有工业产能)的储层品质指数与其产液量的关系,其目的是:(1)依据实际生产数据确定储层产油、产油和产水的储层品质下限值,使得储层的有效性能够得到定量的评价;(2)确定该区域储层品质与储层产液量的关系。
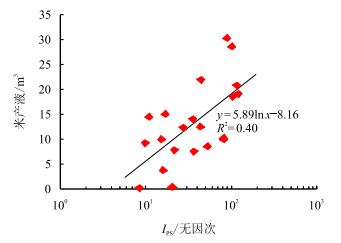
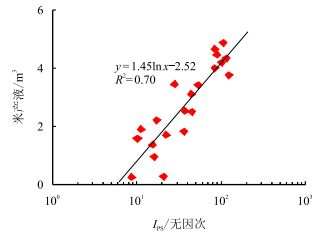
图 6、图 7分别为储层品质指数与日产液量及米产液量(储层米产液量是储层日产液量与储层有效厚度的比值)的关系,可以看出两者均具有正相关性,但储层品质指数与米产液量具有更好的相关性,充分证实了所构建的储层品质指数在反映储层产液能力上具有一定的有效性,储层品质越好的储层,其米产液能力越强,反之亦然。
 |
|
图6
储层品质指数与日产液量的关系
Fig. 6
The relationship between |
 |
|
图7
储层品质与米产液量的关系
Fig. 7
The relationship between |
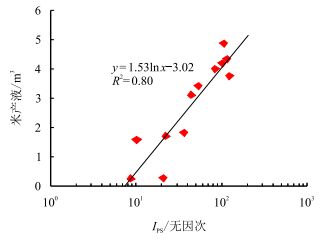
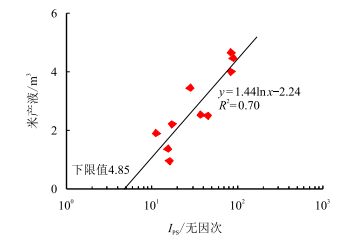
针对储层产油与产油、产水情况,分别建立储层品质与米产液的关系,确定储层品质下限值,如图 8、图 9。储层产油时所确定的储层品质下限值为7.39,储层产油、产水时所确定的储层品质下限值为4.85,认为,当储层品质指数小于下限值时储层的品质极差,储层不具有产液能力,以干层为主,从而不具有开采价值。根据该区工业开采标准,分别建立了储层产油与储层产油、产水两种情况下的产能评价标准,根据其产液能力大小将储层分为4类,具体见表 2、表 3。
 |
|
图8
油层储层品质指数下限值的确定
Fig. 8
Determination of |
 |
|
图9
油水同层储层品质指数下限值的确定
Fig. 9
Determination of |
| 表2 油层产能评价标准 Table 2 Productivity evaluation standard of oil |
| 表3 油水同层产能评价标准 Table 3 Productivity evaluation standard of oil and water |
该储层品质评价方法是基于岩石实验分析及实际试油测试数据建立起来的一套储层分类及产能半定量分析流程,在冀中地区复杂碎屑岩储层评价及认识中利用核磁共振测井提供了有力支撑,其应用主要包括以下3个层面:(1)开展储层有效性评价;(2)对合试层位优选确定主力产层,提出试油建议;(3)对储层的产液能力给出评价。
图 10为冀中地区X1井采用该评价流程处理评价得到的成果图,其中,第1、第3、第4道为常规测井曲线,第5道为标准核磁
 |
| 图10 冀中X1井储层品质及产能评价效果图 Fig. 10 The evaluation result of reservoir quality and productivity |
从计算评价结果来看,28#储层有效孔隙度为22%,渗透率为0.82 mD,储层品质指数1.6,评价结果为Ⅳ类储层,而第123#储层的有效孔隙度为13.4%,渗透率12.30 mD,储层品质指数为29.8,评价结果为Ⅰ类储层。试油结论显示,28#层日产油0.17 m3,水0.27 m3,而123#层日产油18.30 m3。将该技术应用在冀中高阳、马西、文安及廊固地区27口井、共40个层(合试记为单层),35层符合,符合率达到87.5%。
4 结论(1)基于
(2) 构建了储层品质指数,进而建立了区域岩石分类标准,实验数据验证了所构建储层品质指数的合理性。
(3) 确定了区域储层品质下限值及储层品质指数与米产液量的关系,为评价储层有效性及确定储层产液量提供了可靠的实验性及实践性技术支持。
(4) 冀中地区沙河街组沙一段、沙二段的中低孔、低渗透碎屑岩储层的产能分级评价准确率达到87.7%;但该技术在其他地区或者不同岩性及物性情况适应性、可复制性值得进一步研究与检验。
| [1] |
李进步, 付斌, 赵忠军, 等. 苏里格气田致密砂岩气藏储层表征技术及其发展展望[J].
天然气工业, 2015, 35(12): 35–41.
LI Jinbu, FU Bin, ZHAO Zhongjun, et al. Characterization technology for tight sandstone gas reservoirs in the Sulige Gas Field, Ordos Basin, and its development prospect[J]. Natural Gas Industry, 2015, 35(12): 35–41. doi: 10.3787/-j.issn.1000-0976.2015.12.005 |
| [2] |
李宏涛, 史云清, 肖开华, 等. 元坝气田须三段气藏层序沉积与储层特征[J].
天然气工业, 2016, 36(9): 20–34.
LI Hongtao, SHI Yunqing, XIAO Kaihua, et al. Sequence, sedimentary and reservoir characteristics of Xu 3 gas reservoir in the Yuanba Gas Field, NE Sichuan Basin[J]. Natural Gas Industry, 2016, 36(9): 20–34. doi: 10.3787/-j.issn.1000-0976.2016.09.003 |
| [3] |
刘昊伟, 郑兴远, 陈全红, 等. 华庆地区长6深水沉积低渗透砂岩储层特征[J].
西南石油大学学报(自然科学版), 2010, 32(1): 21–26.
LIU Haowei, ZHENG Xingyuan, CHEN Quanhong, et al. Analysis on characteristics of deep-water sedimentary tight sandstone reservoir of Chang 6 in Huaqing area[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(1): 21–26. doi: 10.3863/j.-issn.1674-5086.2010.01.004 |
| [4] |
李志愿. 测井孔隙结构与储层产能关系研究[D]. 青岛: 中国石油大学(华东), 2012, 6875.
LI Zhiyuan. Research on relationship between pore structure and reservoir productivity with logging methods[D].Qingdao:China University of Petroleum, 2012, 68-75. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2087321 |
| [5] |
柴细元, 丁娱娇. 孔隙结构与地层压力相结合的储层产能预测技术[J].
测井技术, 2012, 36(6): 636–640.
CHAI Xiyuan, DING Yujiao. Combination technology of the pore structure and formation pressure for productivity prediction[J]. Well Logging Technology, 2012, 36(6): 636–640. doi: 10.16489/j.issn.1004-1338.2012.06.017 |
| [6] | YAKOV V, LOOYESTIJN W J, SLIJKERMAN W F J, et al. A practical approach to obtain primary drainage capillary pressure curves from NMR core and log data[J]. Petrophysics, 2001, 42(4): 334–343. |
| [7] |
运华云, 赵文杰, 刘兵开, 等. 利用T2分布进行岩石孔隙结构研究[J].
测井技术, 2002, 26(1): 18–21.
YUN Huayun, ZHAO Wenjie, LIU Bingkai, et al. Researching rock pore structure with T2 distribution[J]. Well Logging Technology, 2002, 26(1): 18–21. doi: 10.16489/-j.issn.1004-1338.2002.01.007 |
| [8] |
赵杰, 姜亦忠, 王伟男, 等. 用核磁共振技术确定岩石孔隙结构的实验研究[J].
测井技术, 2003, 27(3): 185–188.
ZHAO Jie, JIANG Yizhong, WANG Weinan, et al. Investigation of rock pore structure using NMR technology[J]. Well Logging Technology, 2003, 27(3): 185–188. doi: 10.-16489/j.issn.1004-1338.2003.03.004 |
| [9] |
何雨丹, 毛志强, 肖立志, 等. 利用核磁共振T2分布构造毛管压力曲线的新方法[J].
吉林大学学报(地球科学版), 2005, 35(2): 177–181.
HE Yudan, MAO Zhiqiang, XIAO Lizhi, et al. A new method to obtain capillary pressure curve using NMR T2 distribution[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(2): 177–181. doi: 10.13278/j.cnki.jjuese.-2005.02.008 |
| [10] |
邵维志, 丁娱娇, 刘亚, 等. 核磁共振测井在储层孔隙结构评价中的应用[J].
测井技术, 2009, 33(1): 52–56.
SHAO Weizhi, DING Yujiao, LIU Ya, et al. The application of NMR log data in evaluation of reservoir pore structure[J]. Well Logging Technology, 2009, 33(1): 52–56. doi: 10.16489/j.issn.1004-1338.2009.01.020 |
| [11] |
赵毅, 施振飞, 朱立华, 等. 构造毛管压力曲线法在A油田储层评价中的应用[J].
复杂油气藏, 2014(1): 52–57.
ZHAO Yi, SHI Zhenfei, ZHU Lihua, et al. Application of capillary pressure curve construction method in the reservoir evaluation of A Oilfield[J]. Complex Hydrocarbon Reservoirs, 2014(1): 52–57. doi: 10.16181/j.cnki.fzyqc.-2014.01.011 |
| [12] |
李鹏举, 谷雨峰. 核磁共振T2谱转换伪毛管压力曲线的矩阵方法[J].
天然气地球科学, 2015, 26(4): 700–705.
LI Pengju, GU Yufeng. Matrix method of transforming NMR T2 spectrum to pseudo capillary pressure curve[J]. Natural Gas Geoscience, 2015, 26(4): 700–705. doi: 10.-11764/j.issn.1672-1926.2015.04.0700 |
| [13] |
闫建平, 温丹妮, 李尊芝, 等. 基于核磁共振测井的低渗透砂岩孔隙结构定量评价方法——以东营凹陷南斜坡沙四段为例[J].
地球物理学报, 2016, 59(4): 1543–1552.
YAN Jianping, WEN Danni, LI Zunzhi, et al. The quantitative evaluation method of low permeable sandstone pore structure based on nuclear magnetic resonance (NMR) logging[J]. Chinese Journal of Geophysics, 2016, 59(4): 1543–1552. doi: 10.6038/cjg20160434 |
| [14] | ZHOU C, LIU Z, SHI Y, et al. Applications of NMR logs to complex lithology interpretation of Ordos Basin[C]. Texas:SPWLA 48th Annual Logging Symposium, 2007. |
| [15] |
徐风, 白松涛, 赵建斌, 等. 一种基于孔隙分量组合下的渗透率计算方法[J].
石油天然气学报(江汉石油学院学报), 2013, 35(11): 76–80, 93.
XU Feng, BAI Songtao, ZHAO Jianbin, et al. A method of calculating permeability based on combination of components[J]. Journal of Oil and Gas Technology, 2013, 35(11): 76–80, 93. |
| [16] |
司兆伟, 赵建斌, 白松涛, 等. 基于岩石物理与核磁测井的储层分类方法研究——以冀东油田某区块为例[J].
石油天然气学报, 2013, 35(12): 73–78.
SI Zhaowei, ZHAO Jianbin, BAI Songtao, et al. Research of reservoir classification by nmr logging based on rock physics[J]. Journal of Oil and Gas Technology (J. JPI), 2013, 35(12): 73–78. doi: 10.3969/j.issn.1000-9752.2013.12.013 |
| [17] |
白松涛, 程道解, 万金彬, 等. 砂岩岩石核磁共振T2谱定量表征[J].
石油学报, 2016, 37(3): 374–378.
BAI Songtao, CHENG Daojie, WAN Jinbin, et al. Quantitative characterization of sandstone NMR T2 spectrum[J]. Acta Petrolei Sinica, 2016, 37(3): 374–378. doi: 10.7623/-syxb201603010 |
| [18] |
刘堂宴, 王绍明, 傅容珊, 等. 核磁共振谱的岩石孔喉结构分析[J].
石油地球物理勘探, 2003, 38(3): 328–333.
LIU Tangyan, WANG Shaoming, FU Rongshan, et al. Analysis of rock pore throat structure with NMR spectra[J]. Oil Geophysical Prospecting, 2003, 38(3): 328–333. doi: 10.13810/j.cnki.issn.1000-7210.2003.03.022 |
| [19] |
于秀英, 古正富, 贾俊杰, 等. 储层孔隙结构测井表征的新方法[J].
非常规油气, 2016, 3(1): 14–20.
YU Xiuying, GU Zhengfu, JIA Junjie, et al. New method of reservoir pore structure logging characterization[J]. Unconventional Oil & Gas, 2016, 3(1): 14–20. |
| [20] |
张冲, 毛志强, 金燕. 基于实验室条件下的核磁共振测井束缚水饱和度计算方法研究[J].
核电子学与探测技术, 2010, 30(4): 514–516.
ZHANG Chong, MAO Zhiqiang, JIN Yan. experimental studies of nmr logging irreducible water saturation[J]. Nuclear Electronics & Detection Technology, 2010, 30(4): 514–516. |
| [21] |
张冲, 张超谟, 张占松, 等. 致密气储层岩心束缚水饱和度实验对比[J].
天然气地球科学, 2016, 27(2): 352–358.
ZHANG Chong, ZHANG Chaomo, ZHANG Zhansong, et al. Comparative experimental study of the core irreducible water saturation of tight gas reservoir[J]. Natural Gas Geoscience, 2016, 27(2): 352–358. doi: 10.11764/j.issn.1672-1926.2016.02.0352 |
| [22] | COATES G R, MARDON D, MARSCHALL D, et al. A new characterization of bulk volume irreducible using magnetic resonance[J]. Log Analysts, 1998, 39(1): 51–63. |
| [23] |
郑庆华, 柳益群. 特低渗透储层微观孔隙结构和可动流体饱和度特征[J].
地质科技情报, 2015, 34(4): 124–131.
ZHENG Qinghua, LIU Yiqun. Microscopic pore structure and movable fluid saturation of ultra low permeability reservoir[J]. Geological Science and Technology Information, 2015, 34(4): 124–131. |
| [24] |
韦青, 李治平, 白瑞婷, 等. 微观孔隙结构对致密砂岩渗吸影响的试验研究[J].
石油钻探技术, 2016, 44(5): 109–115.
WEI Qing, LI Zhiping, BAI Ruiting, et al. An experimental study on the effect of microscopic pore structure on spontaneous imbibition in tight sandstones[J]. Petroleum Drilling Techniques, 2016, 44(5): 109–115. doi: 10.-11911/syztjs.201605019 |
| [25] |
万金彬, 白松涛, 郭笑锴, 等. 南堡凹陷深层低孔隙度低渗透率储层产能预测方法[J].
测井技术, 2015, 32(3): 382–392.
WAN Jinbin, BAI Songtao, GUO Xiaokai, et al. Productivity prediction methods of low porosity and permeability in deep reservoir in Nanpu Sag[J]. Well Logging Technology, 2015, 32(3): 382–392. doi: 10.16489/j.issn.1004-1338.2015.03.022 |
| [26] |
苏俊磊, 孙建孟, 苑吉波, 等. 基于核磁共振孔隙结构的产能评价[J].
西安石油大学学报(自然科学版), 2011, 26(3): 44–47.
SU Junlei, SUN Jianmeng, YUAN Jibo, et al. Reservoir productivity evaluation based on NMR pore structure[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2011, 26(3): 44–47. |
 2018, Vol. 40
2018, Vol. 40