理想气相反应平衡计算有很广泛的用途,例如在炼厂、含硫天然气净化厂等石化企业中广泛应用克劳斯硫磺回收工艺中的克劳斯反应,便可以视为复杂均相的理想气相反应。最小自由能法是计算该问题的一种重要的方法,该方法将平衡问题转化为非线性约束优化问题[1-2],具有如下优点:反应产物组分的数量不受限制[3];计算结果与复杂的中间化学反应过程无关;结果优于平衡常数法[4]。
自20世纪50年代起,国内外学者对最小自由法及其求解方法进行了研究。该问题的求解方法主要可以分为3类:(1)用线性规划或二次规划来逐次逼近非线性优化问题的方法,如分段线性化方法[5]、序列二次规划法[6-7];(2)将约束优化问题转化为无约束优化问题的方法,如惩罚函数法[8-10]、拉格朗日乘数法[3, 11-15]、Powell法[16];(3)对约束优化问题直接进行处理的方法,如变尺度投影法[17]、共轭梯度投影法[18]、梯度投影法[1]、广义简约梯度法[19]。但是由于该优化问题的强非线性,目前的方法在求解该问题时均存在一定的不足,在初值选取、计算速度和计算精度方面仍存在改进空间。本文在对梯度投影法和拉格朗日乘数法分析的基础之上,将二者结合在一起,形成一种新算法:梯度投影-拉格朗日算法,该算法避免了人为选取计算初值,并能保证较快的计算速度和较好的计算精度。
1 最小自由能法最小自由能法由White等人于1958年提出[5]。热力学第二定律指出,体系在给定的温度和压力下,处于平衡状态时,其Gibbs自由能最小。
设体系的组分数为
| $ G = \mathop \sum \limits_{i = 1}^K n_i \mu _i $ | (1) |
式中:
组分
| $ {\mu _i} = \mu _i^\ominus + {\rm{R}}T\ln \frac{{{p_i}}}{{{p^\ominus }}} $ | (2) |
式中:
R—理想气体常数,R=8.314 J·(mol·K)-1;
其中,
| $ \mu _i^ \ominus {\rm{ = }}\Delta _{\rm{f}} G_i^ \ominus $ | (3) |
式中:
对于实际气体,用逸度
| $ \mu _i = \Delta _{\rm{f}} G_i^ \ominus + {\rm{R}}T\ln {\dfrac{{\gamma _i py_i }}{{p^ \ominus }}} $ | (4) |
式中:
对于理想气体
| $ \mu _i = \Delta _{\rm{f}} G_i^ \ominus + {\rm{R}}T\ln{\dfrac{{\gamma _i py_i }}{{p^ \ominus }}} = \Delta _{\rm{f}} G_i^ \ominus + {\rm{R}}T\ln {\dfrac{{py_i }}{{p^ \ominus }}} =\\\hspace{3em} \Delta _{\rm{f}} G_i^ \ominus + {\rm{R}}T\ln \left( {\dfrac{p}{{p^ \ominus }}\dfrac{{n_i }}{{\sum\limits_{i = 1}^K {n_i } }}} \right) $ | (5) |
当体系达到平衡时,
| $ \left\{ \begin{array}{l} \min {\rm{ }}G = \mathop \sum \limits_{i = 1}^K n_i \left[{\Delta _{\rm{f}} G_i^ \ominus + {\rm{R}}T\ln \left( {\dfrac{p}{{p^ \ominus }}\dfrac{{n_i }}{{\sum\limits_{i = 1}^K {n_i } }}} \right)_i } \right] \\ {\rm{s.t.}}~~~~~n_i \geqslant 0~~~~~i = 1, 2, 3, \cdots, K \\ {\rm{ }}\sum\limits_{i = 1}^K {\beta _{ji} n_i = \omega _j }~~~~~~j = 1, {\kern 1pt} 2{\kern 1pt}, {\kern 1pt} 3{\kern 1pt}, \cdots, {\kern 1pt} W \\ \end{array} \right. $ | (6) |
要使上述最优化问题具有实际意义,还需要加入能量平衡方程[14]
| $ Q = {H_{\rm{P}}} - {H_{\rm{R}}} = \sum\limits_{i = 1}^K {{n_i}{H_i}\left( T \right)} - {H_{\rm{R}}} $ | (7) |
式中:
拉格朗日乘数法是处理最小自由能法的经典方法,一般采用牛顿类算法求解,牛顿类算法计算速度快且计算精度高,但由于其本质是局部线性化,初值需要接近真值,即体系的初始状态需要接近平衡状态才能保证计算收敛。梯度投影法是一种求解具有约束条件的非线性优化问题的有效算法,其初值在可行域中即可满足计算要求,但由于步长的限制,收敛速度得不到保证。
鉴于此,本文在对梯度投影法收敛准则改进的基础之上,首先计算出体系的近似平衡状态,再在该近似平衡状态的基础上,通过牛顿法计算拉格朗日乘数法得到体系精确的平衡状态,这样便将梯度投影法和拉格朗日乘数法结合在一起,形成梯度投影-拉格朗日算法。
2.1 梯度投影法采用梯度投影法求解的具有线性约束的非线性优化问题的一般形式为
| $ \left\{ {\begin{array}{*{20}c} {\min f\left( \boldsymbol{{x}} \right)} \\ {\rm{s.t.}~~~~~\boldsymbol{{A}}\boldsymbol{{x}} \leqslant \boldsymbol{{b}}} \\ {\boldsymbol{{E}}\boldsymbol{{x}} = \boldsymbol{{c}}} \\ \end{array}} \right. $ | (8) |
其中
设
| $ \left\{ {\begin{array}{*{20}{c}} {\min G\left( \boldsymbol{{n}} \right)}\\ {\rm{s.t.}~~~~~ - \boldsymbol{{I}}\boldsymbol{{n}} \leqslant 0}\\ {\mathit{\pmb{β}} \boldsymbol{{n}} = {\textbf{ω}} } \end{array}} \right. $ | (9) |
通过拉格朗日乘数法可以将最小自由法对应的非线性约束优化问题(6)转化为如下非线性方程组的求解问题
| $ {S_i}(\boldsymbol{{X}}) = 0~~~~~~i = 1, 2, \cdots, {\kern 1pt} K + W + 2 $ | (10) |
该非线性方程组中的方程数为
| $ \left\{ \begin{array}{l} {n_{K + 1}}\sum\limits_{i = 1}^K {\left[{\left( {{{\rm{e}}^{{x_i}}}} \right){\beta _{ji}}} \right]} = {\omega _j}~~~~~j = 1, 2, 3, \cdots W\\ {\Delta _{\rm{f}}}G_i^ \ominus + {\rm{R}}T\ln {\dfrac{{{{\rm{e}}^{{x_i}}}p}}{{{p^ \ominus }}}} + \sum\limits_{j = 1}^W {{\lambda _j}} {\beta _{ji}} = 0{\rm{ }}~~~~~i = 1, 2, 3, \cdots {\kern 1pt}, K\\ \sum\limits_{i = 1}^K {{{\rm{e}}^{{x_i}}} = 1} \\ {n_{K + 1}}\sum\limits_{i = 1}^K {{{\rm{e}}^{{x_i}}}{H_i}\left( T \right)} - {H_{\rm{R}}} - Q = 0 \end{array} \right.{\rm{ }} $ | (11) |
式中:
该非线性方程组中的方程数和未知数均为
采用弱收敛准则来判断梯度投影法是否收敛,可加快梯度投影法的计算速度。
对于梯度投影法有如下定理
设
| $ \boldsymbol{{P}} = \boldsymbol{{I}} - {\boldsymbol{{M}}^{\rm{T}}}{(\boldsymbol{{M}}{\boldsymbol{{M}}^{\rm{T}}})^{ - 1}}\boldsymbol{{M}} $ | (12) |
| $ \boldsymbol{{w}} = - {(\boldsymbol{{M}}{\boldsymbol{{M}}^{\rm{T}}})^{ - 1}}\boldsymbol{{M}}\nabla f\left( \boldsymbol{{x}} \right){\boldsymbol{{w}}^{\rm{T}}} = ({\boldsymbol{{u}}^{\rm{T}}}, {\boldsymbol{{v}}^{\rm{T}}}) $ | (13) |
式中:
设
(1) 若
(2) 若
| $ \hat {\boldsymbol{{P}}} = \boldsymbol{{I}} - \hat{ \boldsymbol{{M}}}^{\rm{T}}{(\hat {\boldsymbol{{M}}}\hat{ \boldsymbol{{M}}}^{\rm{T}})^{ - 1}}\hat {\boldsymbol{{M}}} $ | (14) |
| $ \boldsymbol{{d}} = - \hat {\boldsymbol{{P}}}\nabla f\left( \boldsymbol{{x}} \right) $ | (15) |
则
对于
设
| $ \boldsymbol{{P}}\nabla f\left( \boldsymbol{{x}} \right) = [\boldsymbol{{I}}-{\boldsymbol{{M}}^{\rm{T}}}{(\boldsymbol{{M}}{\boldsymbol{{M}}^{\rm{T}}})^{-1}}\boldsymbol{{M}}]\nabla f\left( \boldsymbol{{x}} \right) = \nabla f\left( \boldsymbol{{x}} \right) +\\\hspace{2em} {\boldsymbol{{M}}^{\rm{T}}}\boldsymbol{{w}} =\nabla f\left( \boldsymbol{{x}} \right) + \boldsymbol{{A}}_1^{\rm{T}}\boldsymbol{{u}} + {\boldsymbol{{E}}^{\rm{T}}}\boldsymbol{{v}} $ | (16) |
则有
| $ \nabla f\left( \boldsymbol{{x}} \right) + \boldsymbol{{A}}_1^{\rm{T}}\boldsymbol{{u}} + {\boldsymbol{{E}}^{\rm{T}}}\boldsymbol{{v}} = {\mathit{\pmb{ε}} _0} $ | (17) |
| $ \nabla [f\left( \boldsymbol{{x}} \right)-{\mathit{\pmb{ε}} _0}\boldsymbol{{x}}] + \boldsymbol{{A}}_1^{\rm{T}}\boldsymbol{{u}} + {\boldsymbol{{E}}^{\rm{T}}}\boldsymbol{{v}} = 0 $ | (18) |
设
| $ \nabla \bar F\left( \boldsymbol{{x}} \right) + \boldsymbol{{A}}_1^{\rm{T}}\boldsymbol{{u}} + {\boldsymbol{{E}}^{\rm{T}}}\boldsymbol{{v}} = 0 $ | (19) |
| $ \boldsymbol{{P}}\nabla \bar F\left( \boldsymbol{{x}} \right) = 0 $ | (20) |
令
| $ {\boldsymbol{{w}}_0} = - {(\boldsymbol{{M}}{\boldsymbol{{M}}^{\rm{T}}})^{ - 1}}\boldsymbol{{M}}\nabla \bar F\left( \boldsymbol{{x}} \right) $ | (21) |
| $ {\boldsymbol{{w}}_0}^{\rm{T}} = ({\boldsymbol{{u}}_0}^{\rm{T}}, {\boldsymbol{{v}}_0}^{\rm{T}}) $ | (22) |
将
在以
| $ \left\{ {\begin{array}{*{20}{c}} {\min {\rm{ }}\bar F(\boldsymbol{{x}}) = f\left( \boldsymbol{{x}} \right) - {\mathit{\pmb{ε}}_0}\boldsymbol{{x}}}\\ {\rm{s.t.}~~~~~\boldsymbol{{A}}\boldsymbol{{x}} \leqslant \boldsymbol{{b}}{\rm{ }}}\\ {\boldsymbol{{E}}\boldsymbol{{x}} = \boldsymbol{{c}}} \end{array}} \right. $ | (23) |
的最优解,设为
对于
| $ f\left( {{\boldsymbol{{x}}_1}} \right) - f({\boldsymbol{{x}}_2}) > 0 $ | (24) |
对于
| $ \bar F({\boldsymbol{{x}}_2}) - \bar F\left( {{\boldsymbol{{x}}_1}} \right) > 0 $ | (25) |
| $ f({\boldsymbol{{x}}_2}) - {\mathit{\pmb{ε}}_0}{\boldsymbol{{x}}_2} - f({\boldsymbol{{x}}_1}) + {\mathit{\pmb{ε}}_0}{\boldsymbol{{x}}_1} > 0 $ | (26) |
| $ f({\boldsymbol{{x}}_1}) - f({\boldsymbol{{x}}_2}) < {\mathit{\pmb{ε}}_0}({\boldsymbol{{x}}_1} - {\boldsymbol{{x}}_2}) $ | (27) |
因此
| $ 0 < f\left( {{\boldsymbol{{x}}_1}} \right) - f({\boldsymbol{{x}}_2}) < {\mathit{\pmb{ε}}_0}({\boldsymbol{{x}}_1} - {\boldsymbol{{x}}_2}) $ | (28) |
将梯度投影法的收敛标准
为了保证梯度投影法的计算速度,要求弱收敛准则
| $ {\boldsymbol{{X}}^{\left( {k + 1} \right)}} = {\boldsymbol{{X}}^{\left( k \right)}} - {\delta ^{\left( {k + 1} \right)}}\nabla S{\left( {{\boldsymbol{{X}}^{\left( k \right)}}} \right)^{ - 1}}S\left( {{\boldsymbol{{X}}^{\left( k \right)}}} \right) $ | (29) |
式中,
在式(8)中,设
| $ \boldsymbol{{A}} = \left[{\begin{array}{*{20}{c}} {\bar {\boldsymbol{{a}}}_1^{\rm{T}}}\\ {\begin{array}{*{20}{c}} {\bar {\boldsymbol{{a}}}_2^{\rm{T}}}\\ \vdots \end{array}}\\ {\bar {{\boldsymbol{{a}}}}_K^{\rm{T}}} \end{array}} \right], E = \left[{\begin{array}{*{20}{c}} {\bar {\boldsymbol{{a}}}_{K + 1}^{\rm{T}}}\\ {\begin{array}{*{20}{c}} {\bar {\boldsymbol{{a}}}_{K + 2}^{\rm{T}}}\\ \vdots \end{array}}\\ {\bar {\boldsymbol{{a}}}_{K + W}^{\rm{T}}} \end{array}} \right] $ | (30) |
其中:
| $ {\bar {\boldsymbol{{a}}}_j} = {\left( {{{\bar {a}}_{j1}}{\kern 1pt} {{\bar {a}}_{j2}}{\kern 1pt} \cdots {\kern 1pt} {{\bar {a}}_{jK}}} \right)^{\rm{T}}}j = 1, 2, \cdots, {\kern 1pt} K + W $ | (31) |
令
| $ \boldsymbol{{B}} = \left( {\begin{array}{*{20}{c}} \boldsymbol{{b}}\\ \boldsymbol{{c}} \end{array}} \right) = \left[\begin{array}{l} {B_1}\\ {B_2}\\ \vdots \\ {B_{K + W}} \end{array} \right] $ |
| $ {\boldsymbol{{J}}_k} = J\left( {{x^{\left( k \right)}}} \right) = \left\{ {j{\rm{|}}\bar {\boldsymbol{{a}}}_j^{\rm{T}}{\boldsymbol{{x}}^{\left( k \right)}} = {B_j}} \right\} $ | (32) |
梯度投影-拉格朗日算法实现步骤
(1) 给定体系的初始温度
| $ \left\{ \begin{array}{l} \min {\rm{ }}\sum\limits_j^W {{{\left[{\mathop \sum \limits_{i = 1}^K \left( {{\beta _{ji}}{n_i}-{\omega _j}} \right) } \right]}^2} } \\ {\rm{s.t.}}~~~~~{n_i} \geqslant 0~~~~~i = 1, 2, 3, {\kern 1pt} \ldots, {\kern 1pt} K \end{array} \right. $ | (33) |
得最优解
(2) 令
(3) 若
| $ \boldsymbol{{w}} = - {({\boldsymbol{{M}}_k}\boldsymbol{{M}}_k^{\rm{T}})^{ - 1}}{\boldsymbol{{M}}_k}\nabla f\left( {{\boldsymbol{{n}}^{\left( k \right)}}} \right) = \left( {\begin{array}{*{20}{c}} \boldsymbol{{u}}\\ \boldsymbol{{v}} \end{array}} \right) $ | (34) |
若
(4) 计算
设
| $ \left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{} f\left( {{\boldsymbol{{n}}^{\left( k \right)}} + \lambda {\boldsymbol{{d}}_k}} \right)}\\ {\rm{s.t.}~~~~~{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \leqslant \lambda \leqslant {\lambda _{\rm{MAX}}}} \end{array}} \right. $ | (35) |
的解,令
(5) 计算
| $ {T_{i + 1}} = {T_i} - \alpha \dfrac{{g({T_i})\Delta T}}{{g({T_i} + \Delta T) - g({T_i})}} $ | (36) |
(6) 如果
(7) 令
(8) 令
| $ \bar {\boldsymbol{{A}}} = \left[{\begin{array}{*{20}{c}} {{S_1}\left( {\boldsymbol{{X}}_1^{(k)}} \right)}\\ {\begin{array}{*{20}{c}} {{S_2}\left( {\boldsymbol{{X}}_1^{(k)}} \right)}\\ \vdots \end{array}}\\ {{S_{K + W + 2}}\left( {\boldsymbol{{X}}_1^{(k)}} \right)} \end{array}\begin{array}{*{20}{c}} {{S_1}\left( {\boldsymbol{{X}}_2^{(k)}} \right)}\\ {\begin{array}{*{20}{c}} {{S_2}\left( {\boldsymbol{{X}}_2^{(k)}} \right)}\\ \vdots \end{array}}\\ {{S_{K + W + 2}}\left( {\boldsymbol{{X}}_2^{(k)}} \right)} \end{array}\begin{array}{*{20}{c}} \cdots \\ {\begin{array}{*{20}{c}} \cdots \\ \ddots \end{array}}\\ \ldots \end{array}\begin{array}{*{20}{c}} {{S_1}\left( {\boldsymbol{{X}}_{K + W + 2}^{(k)}} \right)}\\ {\begin{array}{*{20}{c}} {{S_2}\left( {\boldsymbol{{X}}_{K + W + 2}^{(k)}} \right)}\\ \vdots \end{array}}\\ {{S_{K + W + 2}}\left( {\boldsymbol{{X}}_{K + W + 2}^{(k)}} \right)} \end{array}} \right] $ | (37) |
其中
(9) 解线性方程组
本文以克劳斯反应为例对梯度投影-拉格朗日算法的有效性进行了验证,并将计算结果与梯度投影法和拉格朗日乘数法的计算结果进行了对比;同时分析了梯度投影-拉格朗日算法中关键参数和温度初值对计算时间的影响。
克劳斯反应酸气流量为100 kmol/h,空气流量207.30 kmol/h,入口气体的温度为40 ℃,系统总压151.2 kPa,不计热损失,设反应产物为SO2、CO2、S2、COS、CS2、CO、H2,酸气组成如表 1所示。
| 表1 克劳斯反应酸气组成 Table 1 The composition of Claus reaction acid gas |
梯度投影-拉格朗日算法中取
表 2为文献中及采用不同算法时克劳斯反应的计算结果,从表中可以看出,梯度投影-拉格朗日算法与拉格朗日乘数法的计算结果相同,但是其计算时间要明显小于后者,并且两者均远远小于梯度投影算法,说明梯度投影-拉格朗日算法是有效的,优于拉格朗日乘数法和梯度投影法。
| 表2 克劳斯反应计算结果 Table 2 The calculation results of Claus reaction |
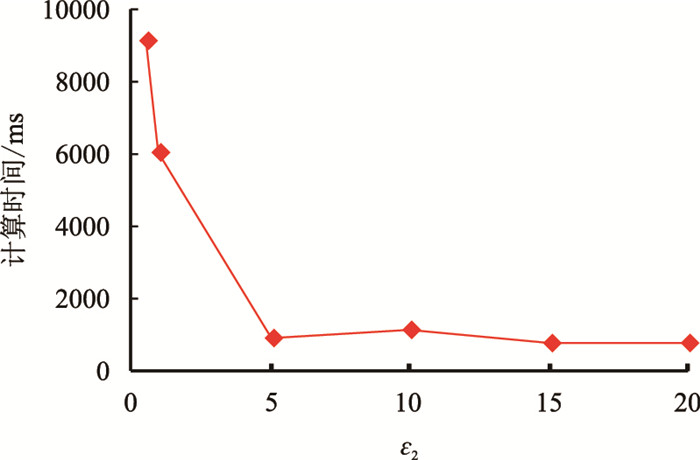
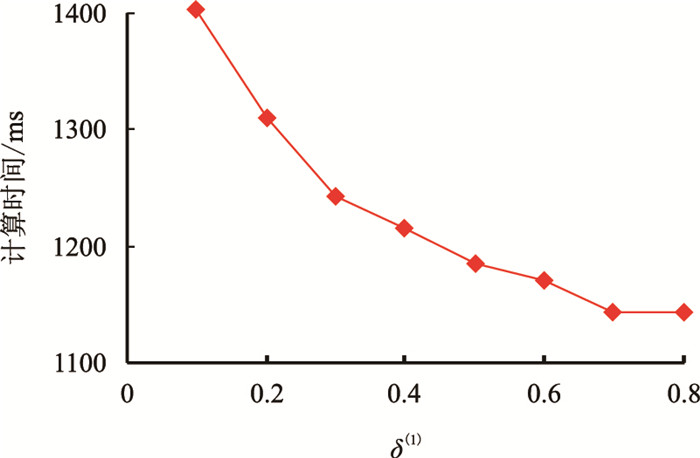
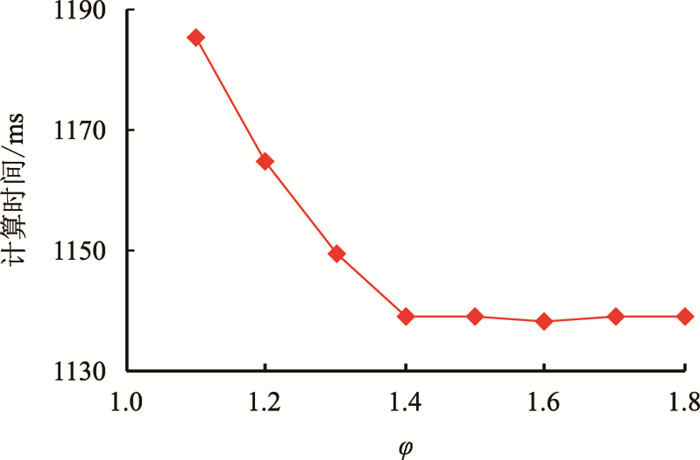
梯度投影-拉格朗日算法中关键参数
 |
|
图1
参数 |
 |
|
图2
参数 |
 |
|
图3
参数 |
 |
|
图4
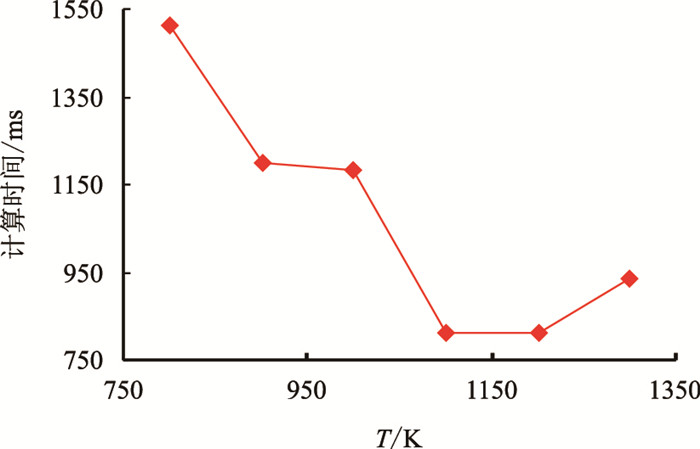
温度初值 |
从图 1~图 3中可以看出,计算时间随着
从图 4可以看出,温度初值
(1) 将梯度投影法的收敛标准
(2) 本文提出了梯度投影-拉格朗日算法,避免了人为选取计算初值,从算例的计算的结果中可以看出该算法的计算速度比拉格朗日乘数法和梯度投影法快,并且计算精度与拉格朗日乘数法相同,在各关键参数大范围变化的情况下,算法的收敛性稳定,说明该算法是一种计算基于最小自由能法的理想气相反应平衡组成的有效方法。
(3) 为了保证算法的收敛性,应控制关键参数
| [1] |
王武谦, 方晨昭, 韩方煜. 多相多组份化学平衡模拟的研究(自由能最小法)[J].
计算机与应用化学, 1990, 7(4): 259–267.
WANG Wuqian, FANG Chenzhao, HAN Fanyu. Study on the equlibrium simulation of multicomponent and mutiphase system (mimizating gibbs free energy)[J]. Computers and Applied Chemistry, 1990, 7(4): 259–267. doi: 10.16866/j.com.app.chem1990.04.004 |
| [2] |
李国栋. 基于Gibbs自由能最小法的反应过程优化设计的研究[D]. 青岛: 中国海洋大学, 2007.
LI Goudong. Study on optimal design of reaction process based on Gibbs free energy minimization method[D]. Qingdao: Ocean University of China, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1070593 |
| [3] |
朱利凯, 鲍钧. 用最小自由能法计算克劳斯反应的平衡组成[J].
石油学报(石油加工), 1990, 6(2): 75–82.
ZHU Likia, BAO Jun. Calculation of equilibrium composition of CLAUS reactions by free energy minimization technique[J]. Acta Petrolei Sinca (Petroleum Processing Section), 1990, 6(2): 75–82. |
| [4] |
杜军驻, 仇汝臣, 冀刚, 等. 克劳斯硫磺回收工艺数学模型的研究[J].
上海化工, 2013, 38(3): 7–12.
DU Junzhu, QIU Ruchen, JI Gang, et al. Study on mathematical model of Claus sulfur recovery process[J]. Shanghai Chemical Industry, 2013, 38(3): 7–12. doi: 10.3969/j.-issn.1004-017X.2013.03.003 |
| [5] | WHITE W B, JOHNSON S M, DANTZIG G B. Chemical equilibrium in complex mixtures[J]. Journal of Chemical Physics, 1958, 28(5): 751–755. doi: 10.1063/1.1744264 |
| [6] | GAUTAM R, SEIDER W D. Computation of phase and chemical equilibrium:Part Ⅰ. Local and constrained minima in Gibbs free energy[J]. Aiche Journal, 2004, 25(6): 991–999. doi: 10.1002/aic.690250610 |
| [7] | LUCIA A, PADMANABHAN L, VENKATARAMAN S. Multiphase equilibrium flash calculations[J]. Computers and Chemical Engineering, 2000, 24(12): 2557–2569. doi: 10.1016/S0098-1354(00)00563-9 |
| [8] |
郭汉杰, 赵玉祥. 最小自由能原理的SUMT方法[J].
北京科技大学学报, 1992, 14(5): 502–508.
GUO Hanjie, ZHAO Yuxiang. Method of minimizing the global free energy with SUMT program[J]. Journal of University of Science and Technology Beijing, 1992, 14(5): 502–508. doi: 10.13374/j.issn1001-053x.1992.05.002 |
| [9] |
许小平, 张唯, 李欣. 惩罚函数法计算燃烧产物的平衡组分[J].
宇航学报, 1994, 15(3): 90–95.
XU Xiaoping, ZHANG Wei, LI Xin. Calculation of equilibrium composition of combustion products by penalty method[J]. Journal of Astronautics, 1994, 15(3): 90–95. |
| [10] | NÉRON A, LANTAGNE G, MARCOS B. Computation of complex and constrained equilibria by minimization of the Gibbs free energy[J]. Chemical Engineering Science, 2012, 82: 260–271. doi: 10.1016/j.ces.2012.07.041 |
| [11] | GORDON S. Computer program for calculation of complex chemical equilibrium compositions, rocket performance incident and reflected shocks and ChapmanJouguet detonation[C]. NASA SP-273, 1971. |
| [12] |
金汀. 用最小自由能法计算克劳斯工艺过程[J].
天然气工业, 1992, 12(2): 66–70.
JIN Ding. Calculating the CLAUS technology process by use of minimum free energy method[J]. Natural Gas Industry, 1992, 12(2): 66–70. |
| [13] |
徐金火, 汤渭龙, 沈复. 克劳斯硫磺回收流程的工艺模拟[J].
石油大学学报(自然科学版), 1993, 17(5): 93–99.
XU Jinhuo, TANG Weilong, SHEN Fu. Flowsheet simulation for CLAUS recovery process of sulfur[J]. Journal of the University of Petroleum, China, 1993, 17(5): 93–99. |
| [14] |
黄河, 李政, 倪维斗. Gibbs反应器模型及其计算机实现[J].
动力工程, 2004, 24(6): 902–907.
HUANG He, LI Zheng, NI Weidou. The Gibbs reactor model and its realization on the computer[J]. Power Engineering, 2004, 24(6): 902–907. doi: 10.3321/j.issn:1000-6761.2004.06.031 |
| [15] |
高磊, 翟悦, 聂颖, 等. 自由能最小化方法处理化学激光器燃烧产物组份的探讨[J].
舰船防化, 2009(1): 43–47.
GAO Lei, ZHAI Yue, NIE Ying, et al. Discussion on method of minimum Gibbs'free energy dealing with compositions of combustion products in chemical laser[J]. Chemical Defence on Ships, 2009(1): 43–47. |
| [16] | GEORGE B, BROWN L P, FARMER C H, et al. Computation of multicomponent, multiphase equilibrium[J]. Industrial & Engineering Chemistry Process Design & Development, 1976, 15(3): 163–169. doi: 10.-1021/i260059a003 |
| [17] |
周维彪, 许志宏. 多相多组元化学平衡相平衡计算(Ⅰ)——算法M-SVMP[J].
化工学报, 1987, 38(1): 39–48.
ZHOU Weibiao, XU Zhihong. Calculation of multicomponent multiphase equilibria (Ⅰ)-Modified algorithm MSVMP method[J]. Journal of Chemeical Industry and Engineering (China), 1987, 38(1): 39–48. |
| [18] |
周维彪, 许志宏. 多相多组元化学平衡相平衡计算(Ⅱ)——新算法GCG法[J].
化工学报, 1987, 38(1): 49–55.
ZHOU Weibiao, XU Zhihong. Calculation of multicomponent multiphase equilibria (Ⅱ)-A new general method GCG[J]. Journal of Chemeical Industry and Engineering (China), 1987, 38(1): 49–55. |
| [19] | SILVA A L D, MALFATTI C D F, MÜLLER I L. Thermodynamic analysis of ethanol steam reforming using Gibbs energy minimization method:A detailed study of the conditions of carbon deposition[J]. International Journal of Hydrogen Energy, 2009, 34(10): 4321–4330. doi: 10.1016/j.ijhydene.2009.03.029 |
| [20] | 唐焕文, 秦学志. 实用最优化算法[M]. 大连: 大连理工大学出版社, 2007: 183-184. |
| [21] |
刘停战, 刘伟, 何颖. 调整步长牛顿法[J].
中国传媒大学学报(自然科学版), 2012, 19(1): 8–10.
LIU Tingzhan, LIU Wei, HE Ying. Step-adjusting newton method[J]. Journal of Communication University of China Science and Technology, 2012, 19(1): 8–10. doi: 10.3969/-j.issn.1673-4793.2012.01.002 |
 2018, Vol. 40
2018, Vol. 40


