2. 海相储层演化与油气富集机理教育部重点实验室, 北京 海淀 100083;
3. 非常规天然气地质评价及开发工程北京市重点实验室, 北京 海淀 100083
2. Key Laboratory of Marine Reservoir Evolution and Hydrocarbon Enrichment Mechanism, Ministry of Education, China University of Geosciences, Haidian, Beijing 100083, China;
3. Beijing Key Laboratory of Unconventional Natural Gas Geological Evaluation and Development Engineering, China University of Geosciences, Haidian, Beijing 100083, China
近年来,随着油气藏地质条件趋于复杂化以及陆上油气当量的不断衰减,定向井以及部分射开井的应用越来越广泛。在实际生产过程中,一方面,定向井在海上油气藏中的应用较多,不少学者[1-3]对斜井和水平井的开发设计以及增产效果进行相关研究;另一方面,在气顶油藏以及底水油藏中,部分射开井可以有效地避免气体和水体过早突进。
前人对部分射开井以及斜井开展了一些相关研究。Cinco应用点源函数、镜像反演以及积分等方法,计算出了上下边界封闭、水平方向无限延伸的板状储层中斜井的解,并给出了表皮因子的近似公式[4-5];Besson也通过理论分析和计算给出了一种斜井的表皮模型[6];Kuchuk等对部分射开井进行过研究与计算,并给出了相应的表皮模型的解析解形式[7-10];Gringarten等也通过点源函数和积分的方法计算出了部分射开储层中水平裂缝的压力解[11];Buhidma等针对底水驱的部分射开直井做了详细研究[12];Brons等也给出了部分射开井的一种表皮模型,并分析了表皮因子和产能的影响因素[13];Yeh等给出了直井穿过多层储层并考虑层间流体的窜流时该井的表皮因子模型[14];王建平通过建立部分射开直井渗流的物理模型和数学模型,利用Laplace变换、Fourier变换以及Stehfest数值反演等数学方法对数学模型进行求解,同时给出了各向异性因子以及射开程度对压力动态的影响[15];李龙龙等通过改进McLeod的射孔几何模型为双径向流,运用等值渗流阻力法计算出部分射开直井的产能公式[16]。然而,目前对部分射开斜井表皮因子的研究较少,甚至没有给出具体的定量表达式,因此,针对部分射开斜直井表皮因子的理论研究具有非常重要的意义。
1 数学模型的建立及其求解如图 1所示,假设流体是微可压缩的,忽略重力、毛管力的影响。考虑顶、底封闭水平方向无限大的均质油藏中有一口部分射开斜井,且位于储层中心,储层垂向与水平方向渗透率不同。储层中任意一点M坐标为(
 |
| 图1 顶底封闭的无限大储层中部分射开斜直井示意图 Fig. 1 The scheme of a partially-penetrating directionally-drilled well in a slab reservoir |
| $ \left\{ \begin{array}{l} {h_{\rm{w}}} \leqslant \dfrac{h}{{\cos {\theta _{\rm{w}}}}}\\[5pt] \dfrac{{{h}_{{\rm w}}}}{2} \leqslant \dfrac{{{z}_{{\rm w}}}}{\cos {{\theta }_{{\rm w}}}}\\[5pt] \dfrac{{{h}_{{\rm w}}}}{2} \leqslant \dfrac{\left( h-{{z}_{{\rm w}}} \right)}{\cos {{\theta }_{{\rm w}}}} \end{array} \right. $ | (1) |
分别定义无因次压力、时间和长度、径向坐标、垂向坐标、储层厚度和井身长度
| $ {{p}_{{\rm D}}}=\dfrac{2{π} {{K}_{{\rm h}}}h({{p}_{{\rm i}}}-p)}{q\mu B} $ | (2) |
| $ {{t}_{{\rm D}}}=\dfrac{2{π} {{K}_{{\rm h}}}t}{\phi \mu {{c}_{{\rm t}}}r_{{\rm w}}^{2}} $ | (3) |
| $ {{h}_{{\rm D}}}=\dfrac{h}{{{r}_{{\rm w}}}}\sqrt{\dfrac{{{K}_{{\rm h}}}}{{{K}_{{\rm v}}}}} $ | (4) |
| $ {{z}_{{\rm D}}}=\dfrac{z}{{{r}_{{\rm w}}}}\sqrt{\dfrac{{{K}_{{\rm h}}}}{{{K}_{{\rm v}}}}} $ | (5) |
| $ {{z}_{{\rm wD}}}=\dfrac{{{z}_{{\rm w}}}}{{{r}_{{\rm w}}}}\sqrt{\dfrac{{{K}_{{\rm h}}}}{{{K}_{{\rm v}}}}} $ | (6) |
| $ {{h}_{{\rm wD}}}=\dfrac{{{h}_{{\rm w}}}}{{{r}_{{\rm w}}}}\sqrt{\dfrac{{{K}_{{\rm h}}}}{{{K}_{{\rm v}}}}{{\cos }^{2}}{{\theta }_{{\rm w}}}+{{\sin }^{2}}{{\theta }_{{\rm w}}}} $ | (7) |
| $ {{r}_{{\rm D}}}=\dfrac{r}{{{r}_{{\rm w}}}} $ | (8) |
定义储层渗透率各向异性因子为
| $ \beta =\sqrt{\dfrac{{{K}_{{\rm h}}}}{{{K}_{{\rm v}}}}} $ | (9) |
拉氏变换后的井斜角为
| $ {{{\theta }'}_{{\rm w}}}={\rm arctan}\left( \sqrt{\dfrac{{{K}_{{\rm v}}}}{{{K}_{{\rm h}}}}}\tan {{\theta }_{{\rm w}}} \right) $ | (10) |
在Laplace空间中无限大储层中点汇无因次扩散方程的瞬时点汇解为[17]
| $ \Delta \tilde{p}=\dfrac{q\mu B}{4{π} K{{r}_{{\rm w}}}s}\dfrac{{\rm e}^ {-\sqrt{s}{{R}_{{\rm D}}}}}{{{R}_{{\rm D}}}} $ | (11) |
式(11)中
| $ R_{{\rm D}}^{2}={{({{{r}'}_{{\rm D}}}-{{r}_{{\rm D}}}\cos \theta )}^{2}}+r_{{\rm D}}^{2}{{\sin }^{2}} $ | (12) |
| $ K=\sqrt{{{K}_{{\rm v}}}\cdot {{K}_{{\rm h}}}} $ | (13) |
在瞬时点汇解的基础之上,利用镜像反演、叠加原理即可得到顶、底边界封闭的无限大储层中的瞬时点汇解为
| $ \begin{array}{l} \Delta \tilde{p}=\dfrac{q\mu B}{4{π} K{{r}_{{\rm w}}}s}\\\sum\limits_{{n}={\rm -}\infty }^{+\infty } \left[\dfrac{{\rm e}^{-\sqrt{{\rm s}}\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}} }}{\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}}}+ \dfrac{{\rm e}^{-\sqrt{{\rm s}}\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}+{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}} }}{\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}+{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}}} \right] \end{array} $ | (14) |
由于存在式(15)的数学关系
| $ \sum\limits_{n=-\infty }^{+\infty }{\dfrac{{\rm e}^{ {\rm -}\sqrt{{\rm s}}\sqrt{{{a}^{2}}+{{\left( \xi -2n{{\xi }_{{\rm e}}} \right)}^{2}}} }}{\sqrt{{{a}^{2}}+{{\left( \xi -2n{{\xi }_{{\rm e}}} \right)}^{2}}}}}=\dfrac{{{K_{\rm{0}}}\left(a\sqrt s\right) }}{{{\xi _{\rm{e}}}}} + \\{\kern 40pt}\dfrac{2}{{{\xi _{\rm{e}}}}}\sum\limits_{n = 1}^\infty {{K_{\rm{0}}}\left( {a\sqrt {s + \dfrac{{{n^2}{\pi ^2}}}{{\xi _{\rm{e}}^2}}} } \right)\cos n{π} \dfrac{\xi }{{{\xi _{\rm{e}}}}}} $ | (15) |
所以,式(14)等号右侧两个无限级数求和项可以化简为
| $ %\begin{array}{l} \sum\limits_{{ n}={\rm -}\infty }^{+\infty }{\dfrac{{\rm e}^{ -\sqrt{{\rm s}}\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}} }}{\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}}}} =\dfrac{{{K_{\rm{0}}}\left( {{R_{\rm{D}}}\sqrt s } \right)}}{{{h_{\rm{D}}}}} + \\{\kern 40pt} \dfrac{2}{{{h_{\rm{D}}}}}\sum\limits_{n = 1}^\infty {{K_{\rm{0}}}\left( {{R_{\rm{D}}}\sqrt {s + \dfrac{{{n^2}{{π} ^2}}}{{h_{\rm{D}}^2}}} } \right)\cos n{π} \dfrac{{{z_{\rm{D}}} - {{z'}_{\rm{D}}}}}{{{h_{\rm{D}}}}}} %\end{array} $ | (16) |
| $ \sum\limits_{{ n}={\rm -}\infty }^{+\infty }{\dfrac{{\rm e}^{ -\sqrt{{\rm s}}\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}+{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}} }}{\sqrt{R_{{\rm D}}^{2}+{{\left( {{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}-2n{{h}_{{\rm D}}} \right)}^{2}}}}} =\dfrac{{{K_{\rm{0}}}\left( {{R_{\rm{D}}}\sqrt s } \right)}}{{{h_{\rm{D}}}}} + \\{\kern 40pt} \dfrac{2}{{{h_{\rm{D}}}}}\sum\limits_{n = 1}^\infty {{K_{\rm{0}}}\left( {{R_{\rm{D}}}\sqrt {s + \dfrac{{{n^2}{{π} ^2}}}{{h_{\rm{D}}^2}}} } \right)\cos n{π} \dfrac{{{z_{\rm{D}}} + {{z'}_{\rm{D}}}}}{{{h_{\rm{D}}}}}} $ | (17) |
将式(16)和式(17)代入公式(15),可以得到
| $ %\begin{array}{l} \Delta \tilde{p}=\dfrac{q\mu B}{2{π} K{{h}_{{\rm D}}}{{r}_{{\rm w}}}s}\left [{{K}_{{\rm 0}}}\left( {{R}_{{\rm D}}}\sqrt{s} \right) \right. + \\{\kern 40pt} \sum\limits_{n=1}^{\infty }{{K}_{{\rm 0}}}\left( {{R}_{{\rm D}}}\sqrt{s+\dfrac{{{n}^{2}}{{\pi }^{2}}}{h_{{\rm D}}^{2}}} \right)\cdot \\ \left. {\kern 40pt} \left( \cos n{π} \dfrac{{{z}_{{\rm D}}}-{{{{z}'}}_{{\rm D}}}}{{{h}_{{\rm D}}}}+\cos n{π} \dfrac{{{z}_{{\rm D}}}+{{{{z}'}}_{{\rm D}}}}{{{h}_{{\rm D}}}} \right) \right] %\end{array} $ | (18) |
再根据三角函数的性质,式(18)可以进一步改写为
| $ \Delta \tilde{p}\dfrac{2{π} K{{h}_{{\rm D}}}{{r}_{\rm w}}s}{q\mu B}={{K}_{{\rm 0}}}\left( {{R}_{\rm D}}{{\varepsilon }_{{\rm 0}}} \right)+\\{\kern 40pt}2\sum\limits_{n=1}^{\infty }{{{K}_{{\rm 0}}}\left( {{R}_{\rm D}}{{\varepsilon }_{{\rm n}}} \right)\cos n{π} \dfrac{{{z}_{{\rm D}}}}{{{h}_{\rm D}}}}\cos n{π} \dfrac{{{{{z}'}}_{{\rm D}}}}{{{h}_{\rm D}}} $ | (19) |
式(19)中,
对于求解斜直线汇的问题,首先在斜井上某点P(
| $ s{{\tilde p}_{\rm{D}}} = \dfrac{{{{{\int}}}_{ - {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}^{ + {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}} {{K_0}({R_{\rm{D}}}\sqrt s ){\rm{d}}{{r'}_{\rm{D}}}} }}{{{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}}+\\2\sum\limits_{n = 1}^\infty {{{{\int}}}_{ - {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}^{ + {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}} {{{K_0}({R_{\rm{D}}}{\varepsilon _{\rm{n}}})\cos \dfrac{{n{π} {z_{\rm{D}}}}}{{{h_{\rm{D}}}}}\cos \dfrac{{n{π} {{z'}_{\rm{D}}}}}{{{h_{\rm{D}}}}}{\rm{d}}{r'}_{\rm D}}} } $ | (20) |
又因为
| $ s{{\tilde p}_{\rm{D}}} \!=\! \dfrac{{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}^{ + {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}} {{K_0}({R_{\rm{D}}}\sqrt s ){\rm{d}}{{r'}_{\rm{D}}}} }}{{{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}}+\\2\sum\limits_{n = 1}^\infty{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}}^{ \!+\! {0.5}{h_{{\rm{wD}}}}\sin {{\theta '}_{\rm{w}}}} {{{K_0}({R_{\rm{D}}}{\varepsilon _{\rm{n}}})\cos \dfrac{{n{π} {z_{\rm{D}}}}}{{{h_{\rm{D}}}}} \cos \dfrac{{n{π} {({{z}_{{\rm wD}}}+{{{r}'}_{{\rm D}}}\cot {{{\theta }'}_{{\rm w}}})}}}{{{h_{\rm{D}}}}}{\rm{d}}{r'}_{\rm D}}} } $ | (21) |
利用变量代换的思想,令
| $ s{{\tilde p}_{\rm{D}}} \!=\! \dfrac{{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}}^{ + {0.5}{h_{{\rm{wD}}}}} {{K_0}({R_{\rm{1D}}}\sqrt s ){\rm{d}}{{r'}_{\rm{D}}}} }}{{{h_{{\rm{wD}}}}}}+\\2\sum\limits_{n = 1}^\infty{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}}^{ \!+\! {0.5}{h_{{\rm{wD}}}}} {{{K_0}({R_{\rm{1D}}}{\varepsilon _{\rm{n}}})\cos \dfrac{{n{π} {z_{\rm{D}}}}}{{{h_{\rm{D}}}}} \cos \dfrac{{n{π} {({{z}_{{\rm wD}}}+{{{r}'}_{{\rm D}}}\cos {{{\theta }'}_{{\rm w}}})}}}{{{h_{\rm{D}}}}}{\rm{d}}{r'}_{\rm D}}} } $ | (22) |
Cinco在1974年成功地给出了求解斜井井底压力时的等效压力点坐标,通过对Cinco等效压力点的坐标进行修正,得到了适用于所有射开程度的斜井井底压力等效压力点坐标,具体坐标如式(23)~式(25)所示
| $ {{r}_{{\rm D}}}=\sqrt{1+{{(0.3{{h}_{{\rm wD}}}\sin {{{{\theta }'}}_{{\rm w}}})}^{2}}} $ | (23) |
| $ \theta ={{\cos }^{{\rm -}1}}\left( \dfrac{0.3{{h}_{{\rm wD}}}\sin {{{{\theta }'}}_{{\rm w}}}}{{{r}_{{\rm D}}}} \right) $ | (24) |
| $ {{z}_{{\rm D}}}={{z}_{{\rm wD}}}\pm 0.3{{h}_{{\rm wD}}}\cos {{{\theta }'}_{{\rm w}}} $ | (25) |
式(25)中,加号代表该点位于储层上半层,减号代表该点位于储层下半层。
2 表皮因子的近似解为了得到部分射开斜井的晚期拟表皮因子,令
由于贝塞尔函数K0有如下数学关系
| $ {{K}_{0}}\left( z \right)=-\ln \left( {{\rm e}^{\gamma }}z/2 \right) $ | (26) |
所以,令式(22)的第一项积分为I1,第二项积分为I2,将式(26)的数学关系应用到I1中,可以得到
| $ {{I}_{1}} = \dfrac{1}{{{h_{{\rm{wD}}}}}}{{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}}^{ + {0.5}{h_{{\rm{wD}}}}} {{K_0}({R_{\rm{1D}}}\sqrt s ){\rm{d}}{{r'}_{\rm{D}}}} }} =\\{\kern 40pt} -\dfrac{1}{{{h_{{\rm{wD}}}}}}{{{{\int}}_{ - {0.5}{h_{{\rm{wD}}}}}^{ + {0.5}{h_{{\rm{wD}}}}} {\ln R_{\rm 1D} {\rm{d}}{{r'}_{\rm{D}}}} }} \underbrace { - \ln ({{\rm e}^\gamma }\sqrt s /2)}_{Radial - Flow} $ | (27) |
从I1的表达式中可以发现,第二项对应于完全射开直井平面径向流,则第一项必然是井的部分射开程度和倾斜角度引起的。
因此,斜直井的晚期表皮模型可以写成
| $ {S_{{\rm{PL}}}} =- \dfrac{1}{{{h_{{\rm{wD}}}}}}\int_{ - 0.5{h_{{\rm{wD}}}}}^{{\rm{ + }}0.5{h_{{\rm{wD}}}}} {\ln {R_{{\rm{1D}}}}{\rm{d}}{{r'}_{\rm{D}}}} + \\ \dfrac{2}{{{h_{{\rm{wD}}}}}}\int_{ - 0.5{h_{{\rm{wD}}}}}^{{\rm{ + }}0.5{h_{{\rm{wD}}}}} {\sum\limits_{n = 1}^\infty {{K_0}\left( {\dfrac{{n{π} {R_{{\rm{1D}}}}}}{{{h_{\rm{D}}}}}} \right)\cos \dfrac{{n{π} {z_{\rm{D}}}}}{{{h_{\rm{D}}}}}\cos \dfrac{{n{π} \left( {{z_{{\rm{wD}}}} + {{r'}_{\rm{D}}}\cos {\theta _{\rm{w}}}} \right)}}{{{h_{\rm{D}}}}}} {\rm{d}}{{r'}_{\rm{D}}}} $ | (28) |
由于存在如式(29)所示的数学公式,式(28)可以写成式(30)的形式由贝塞尔函数K0的求和公式(式(27)),式(28)可以写成
| $ \sum\limits_{n=1}^{\infty }{{{K}_{0}}(nx)\cos nxt}=\dfrac{1}{2}\left(\gamma +\\ \ln \dfrac{x}{4{π} }\right)+\dfrac{{π} }{2}\sum\limits_{m = 1}^\infty {\left[{\dfrac{1}{{\sqrt {{x^2} + {{(2m{π} + tx)}^2}} }} + \dfrac{1}{{\sqrt {{x^2} + {{(2m{π}-tx)}^2}} }}-\dfrac{1}{{m{π} }}} \right]} $ | (29) |
| $ {{S}_{{\rm PL}}}=\ln \dfrac{{{\rm e}^{\gamma }}}{4{{h}_{{\rm D}}}}+{{S}_{01}}+{{S}_{03}}+{{S}_{{\rm m1}}}+{{S}_{{\rm m2}}}+{{S}_{{\rm m3}}}+{{S}_{{\rm m4}}}+\\\dfrac{{{h}_{{\rm D}}}}{2{{h}_{{\rm wD}}}}\sum\limits_{m=1}^{\infty }{\left( -\dfrac{2{{h}_{{\rm wD}}}}{m{{h}_{{\rm D}}}} \right)} $ | (30) |
| $ {{S}_{01}}=\dfrac{{{h}_{{\rm D}}}}{2{{h}_{{\rm wD}}}}{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}}{\dfrac{{\rm d}{{{{r}'}}_{{\rm D}}}}{\sqrt{R_{{\rm 1D}}^{2}+{{({{{{r}'}}_{{\rm D}}}\cos {{{{\theta }'}}_{{\rm w}}}+{{d}_{01}})}^{2}}}}} =\\ \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{{\rm{d}}{{r'}_{\rm{D}}}}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{\rm{01}}}}{{r'}_{\rm{D}}} + {a_{{\rm{01}}}}} }}} $ | (31) |
| $ {{S}_{03}}=\dfrac{{{h}_{{\rm D}}}}{2{{h}_{{\rm wD}}}}{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}}{\dfrac{{\rm d}{{{{r}'}}_{{\rm D}}}}{\sqrt{R_{{\rm 1D}}^{2}+{{({{{{r}'}}_{{\rm D}}}\cos {{{{\theta }'}}_{{\rm w}}}+{{d}_{03}})}^{2}}}}} = \\\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{{\rm{d}}{{r'}_{\rm{D}}}}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{\rm{03}}}}{{r'}_{\rm{D}}} + {a_{{\rm{03}}}}} }}} $ | (32) |
| $ {{S}_{\rm m1}}\!=\!\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {R_{{\rm{1D}}}^2 + {{({{r'}_{\rm{D}}}\cos {{\theta '}_{\rm{w}}} + {d_{{{m1}}}})}^2}} }}} } {\rm{d}}{{r'}_{\rm{D}}} \!=\\\! \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{{m1}}}}{{r'}_{\rm{D}}} + {a_{{{m1}}}}} }}} } {\rm{d}}{{r'}_{\rm{D}}} $ | (33) |
| $ {{S}_{\rm m2}}\!=\!\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {R_{{\rm{1D}}}^2 + {{({{r'}_{\rm{D}}}\cos {{\theta '}_{\rm{w}}} + {d_{{{m2}}}})}^2}} }}} } {\rm{d}}{{r'}_{\rm{D}}} \!=\\ \! \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{{m2}}}}{{r'}_{\rm{D}}} + {a_{{{m2}}}}} }}} } {\rm{d}}{{r'}_{\rm{D}}} $ | (34) |
| $ {{S}_{\rm m3}}\!=\!\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {R_{{\rm{1D}}}^2 + {{({{r'}_{\rm{D}}}\cos {{\theta '}_{\rm{w}}} + {d_{{{m3}}}})}^2}} }}} } {\rm{d}}{{r'}_{\rm{D}}} \!=\\\! \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{{m3}}}}{{r'}_{\rm{D}}} + {a_{{{m3}}}}} }}} } {\rm{d}}{{r'}_{\rm{D}}} $ | (35) |
| $ {{S}_{\rm m4}}\!=\!\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {R_{{\rm{1D}}}^2 + {{({{r'}_{\rm{D}}}\cos {{\theta '}_{\rm{w}}} + {d_{{{m4}}}})}^2}} }}} } {\rm{d}}{{r'}_{\rm{D}}} \!=\\ \! \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {{{\int}}_{-0.5{{h}_{{\rm wD}}}}^{+0.5{{h}_{{\rm wD}}}} {\dfrac{1}{{\sqrt {{{r'}_{\rm{D}}}^2 + {b_{{{m4}}}}{{r'}_{\rm{D}}} + {a_{{{m4}}}}} }}} } {\rm{d}}{{r'}_{\rm{D}}} $ | (36) |
| $ {{a}_{{m}k}}=1+{{(0.3{{h}_{{\rm wD}}}\sin {{{\theta }'}_{{\rm w}}})}^{2}}+{{({{d}_{{ m}k}})}^{2}}, \\ {\kern 40pt}(k = 1, 2, \cdots; m = 0, 1, \cdots) $ | (37) |
| $ {{b}_{{ m}k}}=2({{d}_{{ m}k}}\cos {{{\theta }'}_{{\rm w}}}-0.3{{h}_{{\rm wD}}}{{\sin }^{2}}{{{\theta }'}_{{\rm w}}}) \\ {\kern 40pt}(k = 1, 2, \cdots; m = 0, 1, \cdots) $ | (38) |
| $ {{d}_{{ m1}}}=({{z}_{{\rm wD}}}+{{z}_{{\rm D}}})+2m{{h}_{{\rm D}}} $ | (39) |
| $ {{d}_{{m2}}}=({{z}_{{\rm wD}}}+{{z}_{{\rm D}}})-2m{{h}_{{\rm D}}} $ | (40) |
| $ {{d}_{{ m3}}}=({{z}_{{\rm wD}}}-{{z}_{{\rm D}}})+2m{{h}_{{\rm D}}} $ | (41) |
| $ {{d}_{{ m4}}}=({{z}_{{\rm wD}}}-{{z}_{{\rm D}}})-2m{{h}_{{\rm D}}} $ | (42) |
为了使表皮因子的表达式更易于计算,使用a、b和c(
| $ \int\limits_{{}}^{{}}{\dfrac{1}{\sqrt{c{{x}^{2}}+bx+a}}{\rm d}x}=\\{\kern 40pt}\dfrac{1}{\sqrt{c}}\ln \dfrac{2\sqrt{c(c{{x}^{2}}+bx+a)}+2cx+b}{\sqrt{4ac-{{b}^{2}}}} $ | (43) |
因此
| $ {{S}_{01}}= \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{\rm{01}}}}{h_{{\rm{wD}}}} + {a_{{\rm{01}}}})} + {h_{{\rm{wD}}}} + {b_{{\rm{01}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{\rm{01}}}}{h_{{\rm{wD}}}} + {a_{{\rm{01}}}})} - {h_{{\rm{wD}}}} + {b_{{\rm{01}}}}}} $ | (44) |
| $ {{S}_{03}}= \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{\rm{03}}}}{h_{{\rm{wD}}}} + {a_{{\rm{03}}}})} + {h_{{\rm{wD}}}} + {b_{{\rm{03}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{\rm{03}}}}{h_{{\rm{wD}}}} + {a_{{\rm{03}}}})} - {h_{{\rm{wD}}}} + {b_{{\rm{03}}}}}} $ | (45) |
| $ {{S}_{\rm m1}}= \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{{m1}}}}{h_{{\rm{wD}}}} + {a_{{{m1}}}})} + {h_{{\rm{wD}}}} + {b_{{{m1}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{{m1}}}}{h_{{\rm{wD}}}} + {a_{{{m1}}}})} - {h_{{\rm{wD}}}} + {b_{{{m1}}}}}}} $ | (46) |
| $ {{S}_{\rm m2}}= \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{{m2}}}}{h_{{\rm{wD}}}} + {a_{{{m2}}}})} + {h_{{\rm{wD}}}} + {b_{{{m2}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{{m2}}}}{h_{{\rm{wD}}}} + {a_{{{m2}}}})} - {h_{{\rm{wD}}}} + {b_{{{m2}}}}}}} $ | (47) |
| $ {{S}_{\rm m3}}= \dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{{m3}}}}{h_{{\rm{wD}}}} + {a_{{{m3}}}})} + {h_{{\rm{wD}}}} + {b_{{{m3}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{{m3}}}}{h_{{\rm{wD}}}} + {a_{{{m3}}}})} - {h_{{\rm{wD}}}} + {b_{{{m3}}}}}}} $ | (48) |
| $ {{S}_{\rm m4}}=\dfrac{{{h_{\rm{D}}}}}{{2{h_{{\rm{wD}}}}}}\sum\limits_{m = 1}^\infty {\ln \dfrac{{2\sqrt {(0.25h_{{\rm{wD}}}^2 + 0.5{b_{{{m4}}}}{h_{{\rm{wD}}}} + {a_{{{m4}}}})} + {h_{{\rm{wD}}}} + {b_{{{m4}}}}}}{{2\sqrt {(0.25h_{{\rm{wD}}}^2 - 0.5{b_{{{m4}}}}{h_{{\rm{wD}}}} + {a_{{{m4}}}})} - {h_{{\rm{wD}}}} + {b_{{{m4}}}}}}} $ | (49) |
将式(44)~式(49)代入式(30),即可得到简化后的各向异性储层中部分射开斜直井的表皮因子。
3 对比与验证为了验证所得部分射开斜井表皮因子的正确性,分别从完全射开斜井和部分射开直井两个角度加以验证。
3.1 与斜直井表皮的对比验证Cinco[5]于1975年给出了无限大储层中完全射开斜直井的表皮因子近似解,为
| $ {S_{{\rm{C}}}}({{\rm{ \mathsf{ θ} }}_{\rm{w}}}, {h_{\rm{D}}}) \!=\! - {\left( {\dfrac{{{\theta _{\rm{w}}}}}{{41}}} \right)^{2.06}} \!-\! {\left( {\dfrac{{{\theta _{\rm{w}}}}}{{56}}} \right)^{1.865}} \cdot \lg \dfrac{{{h_{\rm{D}}}}}{{100}} $ | (50) |
该公式仅适用于
此外,Besson[6]于1990年通过理论分析和计算对比,推算出如下的表皮解
| $ {S_{{\rm{B}}}}\left( {{r_{\rm{w}}}, h, {\theta _{\rm{w}}}, \beta } \right) \!=\! \ln \left( {\dfrac{{4{{{r}}_{\rm{w}}}}}{{L\beta \gamma }}} \right) + \\{\kern 40pt}\dfrac{h}{{\gamma L}}\ln \left( {\dfrac{{\sqrt {hL} }}{4 r_{{\rm{w}}}} \cdot \dfrac{{2\gamma \sqrt \gamma }}{{1 + \gamma }}} \right) $ | (51) |
| $ \gamma =\sqrt{{{\cos }^{2}}\theta +\dfrac{1}{{{\beta }^{2}}}{{\sin }^{2}}\theta } $ | (52) |
| $ L=\dfrac{h}{\cos {{\theta }_{{\rm w}}}} $ | (53) |
假设部分射开斜直井的射开程度为1,那么本文的表皮模型(式(30)),便可以简化为斜直井的表皮模型,如式(54)所示。
| $ {{S}_{{\rm PL}}}\left( {{{ h}}_{{\rm D}}}{\rm, }{{{ h}}_{{\rm wD}}}{\rm, }{{\theta }_{{\rm w}}}{\rm, }{{{ z}}_{{\rm wD}}} \right) \!=\!\dfrac{{{h}_{{\rm D}}}}{2}\\\left(\ln \dfrac{2\sqrt{\dfrac{1}{4}\!+\!\dfrac{1}{2}{{b}_{01}}+r_{{\rm D}}^{2}+{{{{d}_{01}}}^{2}}}+1+{{b}_{01}}}{2\sqrt{\dfrac{1}{4}-\dfrac{1}{2}{{b}_{01}}+r_{{\rm D}}^{2}+{{{{d}_{01}}}^{2}}}-1+{{b}_{01}}} \\+\ln \dfrac{2\sqrt{\dfrac{1}{4}+\dfrac{1}{2}{{b}_{03}}+r_{{\rm D}}^{2}+{{{{d}_{03}}}^{2}}}+1+{{b}_{03}}}{2\sqrt{\dfrac{1}{4}-\dfrac{1}{2}{{b}_{03}}+r_{{\rm D}}^{2}+{{{{d}_{03}}}^{2}}}-1+{{b}_{03}}}\right) + \\\ln \dfrac{{{\rm e}^{\gamma }}}{4{{h}_{{\rm D}}}} +\dfrac{{{h}_{{\rm D}}}}{2}\sum\limits_{m=1}^{\infty }{\left( \sum\limits_{k=1}^{4}{\ln \dfrac{2\sqrt{\dfrac{1}{4}+\dfrac{1}{2}{{b}_{{ mk}}}+{{a}_{{ mk}}}}+1+{{b}_{{ mk}}}}{2\sqrt{\dfrac{1}{4}-\dfrac{1}{2}{{b}_{{ mk}}}+{{a}_{{ mk}}}}-1+{{b}_{{ mk}}}}}-\dfrac{2}{m{{h}_{{\rm D}}}} \right)} $ | (54) |
令储层厚度h=10 m,rw=0.1 m,
| 表1 3种斜直井表皮模型的对比 Table 1 Comparison of 3 kinds of inclined/vertical well skin models |
 |
| 图2 3种斜直井表皮模型对比图 Fig. 2 Map of 3 kinds of inclined/vertical well skin models |
1987年Kuchuk [7]提出了部分射开直井的表皮模型,为
| $ {{S}_{{\rm K}}}\left( {{h}_{{\rm D}}}, {{h}_{{\rm wD}}}, {{z}_{{\rm wD}}}, \beta \right)=2\sum\limits_{n=1}^{\infty }{\dfrac{{{K}_{0}}({{u}_{n}})}{0.5{{u}_{n}}{{{{h}'}}_{{\rm wD}}}}}\cdot \\ {\kern 40pt}\sin (0.5{{u}_{n}}{{{h}'}_{{\rm wD}}})\cos ({{u}_{n}}{{z}_{{\rm wD}}})\cos ({{u}_{n}}{{z}_{{\rm D}}}) $ | (55) |
式中:
同年,学者Papatzacos[8]也提出了一种部分射开的表皮模型
| $ {{S}_{{\rm P}}}\left( {{h}_{{\rm D}}}, {{h}_{{\rm wD}}}, {{z}_{{\rm wD}}}, \beta \right)=\left(\dfrac{{{h}_{{\rm D}}}}{{{{{h}'}}_{{\rm wD}}}}-1\right)\cdot \\ {\kern 40pt}\ln \left (\dfrac{1}{2}{π} {{h}_{{\rm D}}}\right)+\dfrac{{{h}_{{\rm D}}}}{{{{{h}'}}_{{\rm wD}}}}\ln \left(\dfrac{{{{{h}'}}_{{\rm wD}}}\sqrt{x}}{2{{h}_{{\rm D}}}+{{{{h}'}}_{{\rm wD}}}}\right) $ | (56) |
式中:
假设本文的部分射开斜直井的井斜角度为0,那么本文的表皮模型,就可以简化为部分射开直井的表皮模型
| $ {{S}_{{\rm PL}}}\left( {{{ h}}_{{\rm D}}}{\rm, }{{{ h}}_{{\rm wD}}}{\rm, }{{\theta }_{{\rm w}}}{\rm, }{{{ z}}_{{\rm wD}}} \right) \!=\! \ln \dfrac{{{\rm e}^{\gamma }}}{4{{h}_{{\rm D}}}} +\dfrac{{{h}_{{\rm D}}}}{2h_{\rm wD}}\\\sum\limits_{m=1}^{\infty }{\left( \sum\limits_{k=1}^{4}{\ln \dfrac{2\sqrt{\dfrac{1}{4}{{h_{{\rm{wD}}}^2}}+\dfrac{1}{2}{{b}_{{ mk}}}{{{h_{{\rm{wD}}}}}}+{{a}_{{ mk}}}}+{{{h_{{\rm{wD}}}}}}+{{b}_{{ mk}}}}{2\sqrt{\dfrac{1}{4}{{{h_{{\rm{wD}}}}}^2}-\dfrac{1}{2}{{b}_{{ mk}}}{{{h_{{\rm{wD}}}}}}+{{a}_{{ mk}}}}-{{{h_{{\rm{wD}}}}}}+{{b}_{{ mk}}}}}-\dfrac{2{{h_{{\rm{wD}}}}}}{m{{h}_{{\rm D}}}} \right)}+ \\ \dfrac{{{h}_{{\rm D}}}}{2h_{\rm wD}}\left( \ln \dfrac{{2\sqrt {{\dfrac{1}{4}}h_{{\rm{wD}}}^2 + {\dfrac{1}{2}}{b_{01}}{h_{{\rm{wD}}}} + 1 + {{{d_{01}}}^2}} + {h_{{\rm{wD}}}} + {b_{01}}}}{{2\sqrt {{\dfrac{1}{4}}h_{{\rm{wD}}}^2 - {\dfrac{1}{2}}{b_{01}}{h_{{\rm{wD}}}} + 1 + {{{d_{01}}}^2}} - {h_{{\rm{wD}}}} + {b_{01}}}} \\ + \ln \dfrac{{2\sqrt {{\dfrac{1}{4}}h_{{\rm{wD}}}^2 + {\dfrac{1}{2}}{b_{03}}{h_{{\rm{wD}}}} + 1 + {{{d_{03}}}^2}} + {h_{{\rm{wD}}}} + {b_{03}}}}{{2\sqrt {{\dfrac{1}{4}}h_{{\rm{wD}}}^2 - {\dfrac{1}{2}}{b_{03}}{h_{{\rm{wD}}}} + 1 + {{{d_{03}}}^2}} - {h_{{\rm{wD}}}} + {b_{03}}}} \right) $ | (57) |
令储层厚度h=50 m,rw=0.1 m,
| 表2 3种部分射开直井表皮模型的对比 Table 2 Comparison of 3 kinds of skin models for partially-penetrating vertical wells |
 |
| 图3 部分射开直井表皮模型对比图 Fig. 3 Map of 3 kind of skin factor models for partially-penetrating vertical wells |
一方面,将本文结果与Cinco(井的倾斜角度范围为0~75 °)和Besson的完全射开斜直井表皮模型分别进行对比,另一方面,与Kuchuk和Papatzacos两人的部分射开直井的表皮模型进行对比,两次拟合结果均表明本文的部分射开斜直井表皮新模型具有较高的精确度和应用意义。
4 影响因素分析 4.1 表皮模型影响因素分析部分射开斜直井表皮因子存在多方面的影响因素,包括井斜角度、井身长度、储层厚度以及储层渗透率各向异性因子,故绘制了不同井身长度下表皮因子随井斜角度变化曲线和不同储层各向异性因子下表皮因子随储层厚度变化曲线,分别如图 4与图 5所示。
 |
| 图4 不同井身长度下井斜角度对表皮因子的影响 Fig. 4 The effect of angle on skin factor under different well length |
 |
| 图5 不同渗透率各向异性因子下井身长度对表皮因子的影响 Fig. 5 The effect of well length on skin factor under different anisotropy factor |
在图 4中,储层厚度为10 m,井筒半径为0.1 m,储层各向异性因子为1,井身中点的垂向坐标为5 m。
由图 4可知,当井的长度、储层厚度与储层各向异性因子等参数一定时,部分射开斜直井的表皮因子随着井斜角度的增加而减小,这是因为井斜角度越大,井筒的泄流面积就越大,从而会有利于井的实际生产;当井的倾斜角度、储层厚度与储层各向异性因子等参数一定时,部分射开斜直井的表皮因子随着井的长度增加而减小。值得注意的是:井身长度较长的斜井,井斜角度对表皮因子的影响也越明显,这是因为井身长度较长的斜井,随着角度的不断增大,井筒的泄流面积增加的速度会越快,从而导致其表皮因子的减小速率较大。
在图 5中,井身长度为45 m,井筒半径为0.1 m,井的倾斜角度为30°,井身中点的垂向坐标为5 m。
由图 5可知,当井的长度、井斜角度与储层各向异性因子等参数一定时,表皮因子会随着储层的厚度增大而增大,这相当于射开程度减小从而引起表皮因子增大;当井的倾斜角度、储层厚度与井的长度等参数一定时,表皮因子随着储层各向异性因子的增加而增大,即如果垂向渗透率比水平渗透率小且逐渐减小,那么斜井的表皮因子就越大。此现象表明,当垂向渗透率较小时,增加井的倾斜角度增产效果不明显,但是在均质储层或者垂向渗透率较大的储层中,增加井的倾斜角度会使增产效果更好。
4.2 产能影响因素分析为了研究斜直井产量的影响因素,故引入产量增产倍数J,定义如式(60)所示,并绘制了不同井身长度下产量增产倍数与井斜角度的关系图版和不同储层各向异性因子下产量增产倍数与储层厚度的关系图版,分别如图 6与图 7所示。在图 6中,储层厚度为10 m,井筒半径为0.1 m,影响半径为300 m,渗透率各向异性因子为1,井身中点的垂向坐标为5 m;在图 7中,井身长度为45 m,井筒半径仍为0.1 m,影响半径为300 m,井的倾斜角度为30°,井身中点的垂向坐标为5 m。
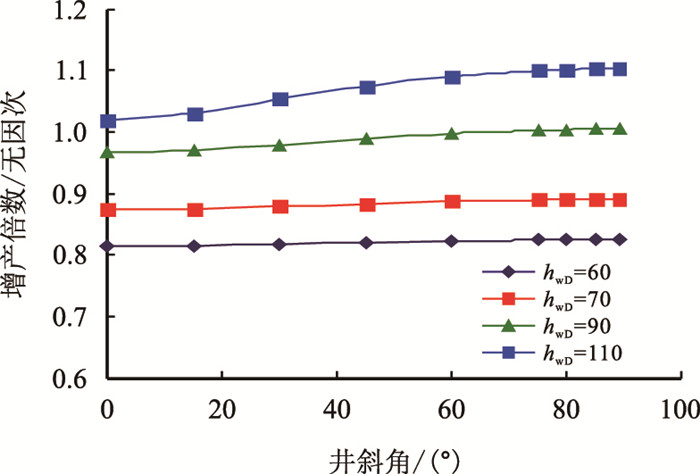 |
| 图6 不同井身长度下井斜角度对产量增长倍数的影响 Fig. 6 The effect of angle on production stimulation ratio under different well length |
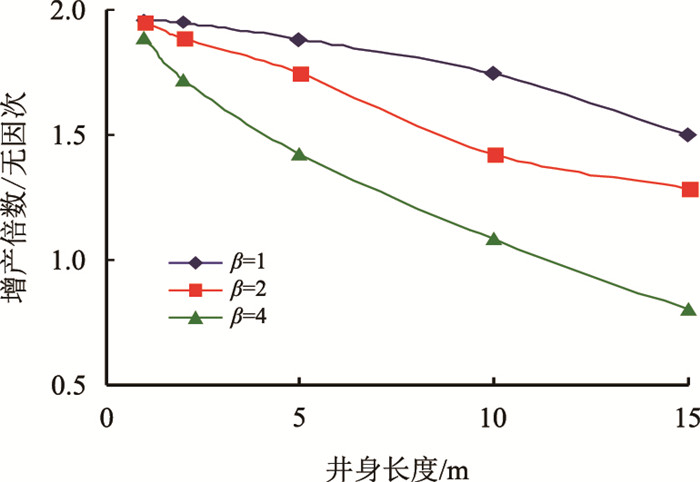 |
| 图7 不同渗透率各向异性因子下井身长度对产量增长倍数的影响 Fig. 7 The effect of well length on production stimulation ratio under different anisotropy factor |
若不考虑机械表皮,普通直井的产能公式为
| $ {{Q}_{{\rm v}}}=\dfrac{2{π} Kh\Delta p}{\mu B\ln ({{r}_{{\rm e}}}/{{r}_{{\rm w}}})} $ | (58) |
斜直井的产能公式为
| $ Q=\dfrac{2{π} Kh\Delta p}{\mu B\ln ({{r}_{{\rm e}}}/{{r}_{{\rm w}}})+{{S}_{{\rm PL}}}} $ | (59) |
故本文的产量增产倍数为
| $ J=\dfrac{Q}{{{Q}_{{\rm v}}}}=\dfrac{\ln \dfrac{{{r}_{{\rm e}}}}{{{{r}}_{{\rm w}}}}}{\ln \dfrac{{{r}_{{\rm e}}}}{{{r}_{{\rm w}}}}+{{S}_{{\rm PL}}}} $ | (60) |
由图 6可知,当井身长度、储层厚度与渗透率各向异性因子等参数一定时,部分射开斜井的产量增长倍数随着井斜角度的增加而增加,这表明井斜角度越大,其泄流面积就越大,产量便会增加,从而会有利于井的实际生产;当井的倾斜角度、储层厚度与储层各向异性因子等参数一定时,部分射开斜直井的产量增长倍数随着井的长度增加而增加,而且井的长度越长,井斜角度对产量增长倍数的影响也越明显。
由图 7可知,当井身长度、井斜角度与渗透率各向异性因子等参数一定时,部分射开斜直井的产量增长倍数随着储层厚度的增加而减小,这表明储层厚度的增大,相当于射开程度的减小,从而使得产量增长倍数减小;当井的倾斜角度、储层厚度与井身长度等参数一定时,部分射开斜直井的产量增长倍数随着储层各向异性因子增加而减小,这表明储层越趋于均质或者垂向渗透率较大,将会越有利于实际生产。
5 结论(1) 对于部分射开斜直井的表皮模型,井身长度和井的倾斜角度的增大都会使得井筒的泄流面积增大,从而使斜井的表皮因子减小。井身长度较长的斜井,随着角度的增大,井筒泄流面积的增长速率也会越快,从而导致表皮因子减小得越快。
(2) 其他条件一定时,储层厚度的增加相当于减小了储层的射开程度,从而使得斜井的表皮因子增大。储层各向异性因子的增大也会使表皮因子增大,这意味着在均质储层或者垂向渗透率比水平渗透率大的储层中,增加井斜角度会使表皮因子明显减小。
(3) 在均质或者垂向渗透率较大的储层中,可以通过尽可能地增加斜井的倾斜角度、井身长度来提高产量增产倍数,从而达到理想的增产效果。
符号说明
r—空间中任意一点的径向坐标,cm;
z—空间中任意一点的垂向坐标,cm;
hw—井身长度,cm;
zw—储层中心点的垂向坐标,cm;
pD—无因次压力;
Kh—水平渗透率,D;
q—井的产量,cm3/s;
B—原油体积压缩系数,无因次;
tD—无因次时间;
ct—储层的压缩系数,atm
rw—井筒半径,cm;
hD—无因次储层厚度;
Kv—垂直渗透率,D;
zD—无因次垂向坐标;
zwD—无因次垂向坐标;
rD—无因次径向坐标;
s—Laplace变量;
SPL—部分射开斜直井表皮因子,无因次;
re—泄油半径,cm;
Q—部分射开斜直井的产量,cm3/s;
| [1] |
齐天俊, 向凌云, 陈亚丽, 等. 川东石炭系大斜度井、水平井增产效果影响因素分析[J].
天然气工业, 2014, 34(S1): 40–44.
QI Tianjun, XIANG Lingyun, CHEN Yali, et al. Analysis of influencing factors for stimulation effect of high-angle wells or horizontal wells in East Sichuan Carboniferous system reservoir[J]. Natural Gas Industry, 2014, 34(S1): 40–44. doi: 10.3787/j.issn.1000-0976.2014.s1.010 |
| [2] |
张宇, 钟海全, 李永臣, 等. 底水气藏大斜度井开发优化设计研究[J].
岩性油气藏, 2015, 27(2): 114–118.
ZHANG Yu, ZHONG Haiquan, LI Yongchen, et al. Optimization of development of highly deviated well in gas reservoir with bottom water[J]. Lithologic Reservoirs, 2015, 27(2): 114–118. doi: 10.3969/j.issn.1673-8926.2015.02.018 |
| [3] |
张迎春, 赵春明, 刘歆, 等. 水平分支井技术在渤海稠油油田开发中的应用[J].
岩性油气藏, 2011, 23(1): 118–122.
ZHANG Yingchun, ZHAO Chunming, LIU Xin, et al. Application of multilateral well technology to development of heavy oil fields in the Bohai Sea[J]. Lithologic Reservoirs, 2011, 23(1): 118–122. doi: 10.3969/j.issn.-1673-8926.2011.01.023 |
| [4] | CINCO-LEY H, MILLER F G, RAMEY H J. Unsteadystate pressure distribution created by a directionally drilled well[J]. SPE 5131-PA, 1975. doi: 10.2118/5131-PA |
| [5] | CINCO-LEY H, MILLER F G, RAMEY H J. Pseudoskin factors for partially-penetrating directionally-drilled wells[C]. SPE 5589-MS, 1975. doi: doi.org/10.2118/-5589-MS |
| [6] | BESSON J, AQUITAINE E. Performance of slanted and horizontal wells on an anisotropic medium[C]. SPE 20965-MS, 1990. doi: doi.org/10.2118/20965-MS |
| [7] | KUCHUK F J, KIRWAN P A. New skin and well bore storage type curves for partially penetrated wells[C]. SPE 11676-PA, 1987. doi: 10.2118/11676-PA |
| [8] | PAPATZACOS P. Approximate partial-penetration pseudoskin for infinite conductivity wells[C]. SPE 13956-PA, 1987. doi: 10.2118/13956-PA |
| [9] | YILDIZ T, BASSIOUNI Z A. Transient pressure analysis in partially-penetrating wells[C]//CIM/SPE International Technical Meeting, Society of Petroleum Engineers, 1990. SPE PETSOC-90-02, 1990. doi: 10.2118/90-02 |
| [10] | CLEGG M W, MILLS M. A study of behavior of partially penetrating wells[C]. SPE 2054-PA, 1969. doi: 10.2118/-2054-PA |
| [11] | GRINGARTEN A C, RAMEY H J Jr. Unsteady-state pressure distributions created by a well with a single horizontal fracture, partial penetration, or restricted entry[C]. SPE 3819-PA, 1974. doi: 10.2118/3819-PA |
| [12] | BUHIDMA I M, RAGHAVAN R. Transient pressure of partially penetrating wells subject to bottom-water drive[C]. SPE 8143-PA, 1980. doi: 10.2118/8143-PA |
| [13] | BRONS F, Marting V E. The effect of restricted fluid entry on well productivity[J]. Journal of Petroleum Technology, 1961, 13(2): 172–174. doi: 10.2118/1322-G-PA |
| [14] | YEH N, Reynolds A C. Computation of the pseudoskin factor caused by a restricted-entry well completed in a multilayer reservoir[C]. SPE 15793-PA, 1989. 10. 2118/-15793-PA |
| [15] |
王建平, 王晓冬, 马世东. 各向异性部分射开直井不稳定渗流理论研究[J].
大庆石油地质与开发, 2007, 26(3): 65–68.
WANG Jianping, WANG Xiaodong, MA Shidong. The research of unsteady flow theory of partially-penetrating wells in anisotropic reservoirs[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26(3): 65–68. doi: 10.3969/j.issn.1000-3754.2007.03.015 |
| [16] |
李龙龙, 吴明录, 姚军, 等. 部分射开直井的产能计算方法[J].
石油钻探与开发, 2014, 42(3): 81–89.
LI Longlong, WU Minglu, YAO Jun, et al. The calculation method of production for partially-penetrating vertical wells[J]. Petroleum Exploration and Development, 2014, 42(3): 81–89. doi: 10.3969/j.issn.10010890.2014.03.016 |
| [17] | GRINGARTEN A C, RAMEY H J Jr. The use of source and green's functions in the solution of unsteady flow problems in reservoirs[J]. Society of Petroleum Engineers Journal, 1973, 13(5): 285–296. doi: 10.2118/3818-PA |
 2018, Vol. 40
2018, Vol. 40


