2. 中国石油煤层气有限责任公司, 北京 朝阳 100028;
3. 中海油研究总院, 北京 朝阳 100028
2. PetroChina Coalbed Methane Co. Ltd., Chaoyang, Beijing 100028, China;
3. CNOOC Research Institute, Chaoyang, Beijing 100028, China
油田注水开发过程中,注入水中过多的悬浮颗粒会堵塞孔隙,引起注入能力和生产状况恶化,此类地层伤害常见于污水回注方式中,基于堵塞机理的地层伤害预测模型可有效指导矿场的注水作业[1]。采用室内岩芯驱替实验可以从岩芯尺度上研究悬浮颗粒在多孔介质中的运移和堵塞机理[2-4],但是只能得到定性结论不能直接用来预测注入水造成的地层伤害,因此许多学者基于实验结果建立了众多考虑不同堵塞机理的地层伤害预测模型[5-7],形成了利用实验岩芯结果解释地层伤害参数(渗滤系数和地层伤害系数)的方法。宏观的预测模型对堵塞机理做了过多的简化假设,而实验模拟方法花费巨大,利用计算机进行悬浮颗粒多孔介质微观运移模拟正逐渐成为堵塞机理研究中的一种快速而有效的研究方法[8]。
1 悬浮颗粒受力分析将注入水中的悬浮颗粒简化为球形,将其看作刚性颗粒便于受力分析。注入水中悬浮颗粒浓度一般较低,属于稀疏颗粒流体流动,因此不用考虑颗粒质量力等。如图 1,悬浮颗粒在流体中只考虑重力、浮力和拖拽力。
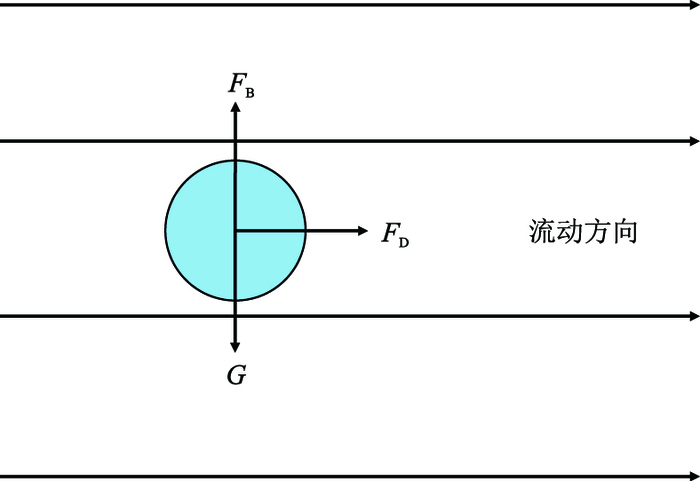 |
| 图1 悬浮颗粒在流体中流动的受力示意图 Fig. 1 Diagram of the acting forces for suspended particles in fluid flow |
悬浮颗粒所受重力为
| $G = \rho _{\rm{p}} V_{\rm{p}} {\rm{g}}$ | (1) |
式中:
g—重力加速度,g=9.8 m/s2。
悬浮颗粒所受到的浮力为
| $F_{\rm{B}} = \rho _{\rm{l}} V_{\rm{p}} {\rm{g}}$ | (2) |
式中:
流体与悬浮颗粒由于速度差引起流体对颗粒的作用力称为拖拽力,计算公式如下[9]
| $F_{\rm{D}} = 6\pi \mu r_{\rm{p}} \left( {v_{\rm{l}} - v_{\rm{p}} } \right)$ | (3) |
式中:
当悬浮颗粒在多孔介质中运移时,悬浮颗粒与骨架颗粒会产生碰撞,侵入悬浮颗粒与骨架颗粒的相互作用近似为两个刚性球体的碰撞过程,如图 2所示,当悬浮颗粒沉积到骨架颗粒表面即两者形成接触时,颗粒间接触模型用来预测颗粒的运动,包括法向接触力和切向接触力。多个悬浮颗粒在通过一定尺度孔喉时有可能产生桥堵现象,由于本文颗粒间相互作用时并没有考虑颗粒与颗粒之间形成架桥封堵时的特殊接触模型,对于架桥封堵的模拟功能暂时还是比较欠缺,所以本模型主要还是考虑孔喉对颗粒的直接滞留的影响。
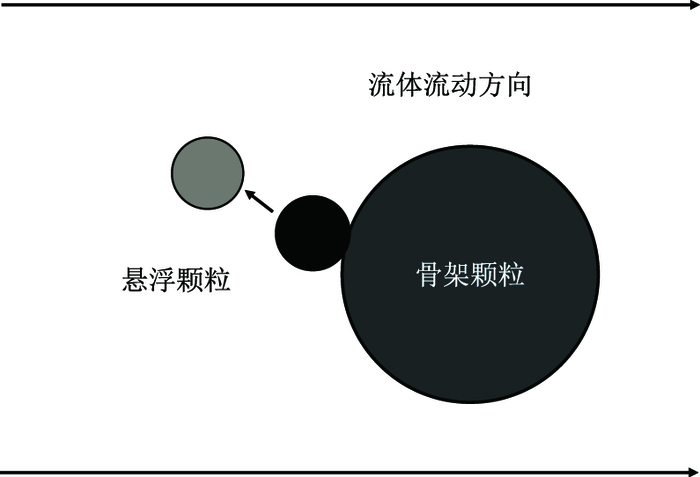 |
| 图2 悬浮颗粒与骨架颗粒碰撞过程示意图 Fig. 2 Diagram of the collision between suspended particles and skeleton particle |
本文采用离散单元方法(DEM)来生成骨架颗粒模型,有半径膨胀法和爆炸排斥法两种方式可以在给定的空间内生成给定孔隙度的多孔介质骨架。利用俄克拉荷马的Antler天然砂岩的力学性质分析结果生成天然岩芯骨架模型[10],Antler天然砂岩岩芯粒径分布如图 3所示,骨架颗粒粒径在0.06~1.00 mm,大约80%骨架颗粒粒径在0.10~0.30 mm,骨架颗粒平均粒径约为0.30 mm。
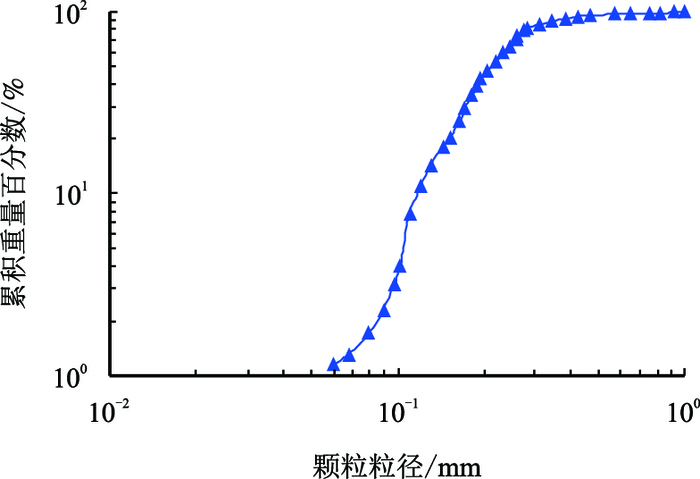 |
| 图3 Antler岩芯颗粒粒径统计分布图 Fig. 3 Diagram of particle diameter statistical distribution for Antler core |
通过仔细选择和调整DEM中颗粒的微观力学性质参数,拟合其宏观力学参数到实验室岩样测试结果,拟合后的骨架颗粒模型便可以作为后续悬浮颗粒运移的基础模型,图 4显示了半径膨胀法最终生成的骨架颗粒模型,当给定围压为6.9 MPa,通过岩样模拟计算得到杨氏模量大约为4.52 GPa,与实验测量结果4.50 GPa较为吻合,其中表 1是最后的颗粒微观力学性质取值。
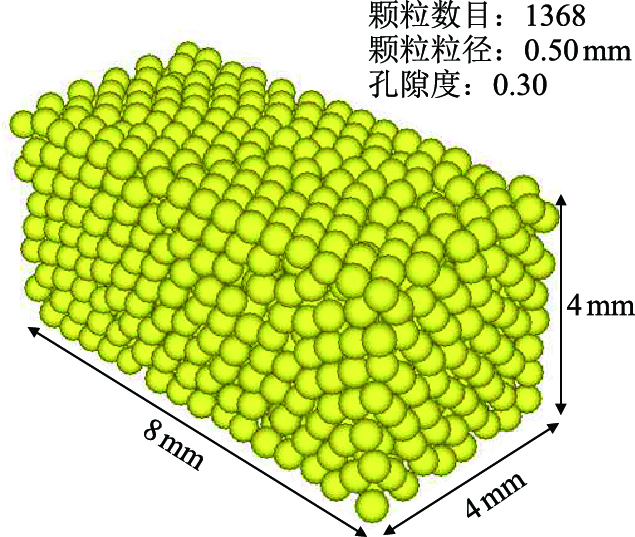 |
| 图4 半径膨胀法生成岩石岩样三维图 Fig. 4 Diagram of 3D core sample by using radius inflation |
| 表1 地层岩样性质参数 Table 1 The parameters for generating the skeleton particle |
离散单元法(DEM)是Cundall于1979年提出的用大量颗粒运动来模拟岩石力学过程的模拟方法[11],基于DEM方法模拟悬浮颗粒在多孔介质中的微观运移及堵塞过程。在DEM的计算中,利用牛顿第二定律计算接触力和体积力下颗粒的运动,利用位移法计算接触变化后的接触力,壁面只需要位移法来描述颗粒壁面接触。牛顿第二定律不会应用于壁面,而是由边界条件确定壁面运动情况。离散单元法每个时间步都会利用颗粒运动定律,接触位移法更新颗粒和壁面位置,根据更新后的位置形成或删除颗粒之间或者壁面与颗粒之间的接触,具体的接触模型和运动模型这里不再赘述。
3.2 骨架颗粒流体耦合模型准确模拟固体骨架颗粒变形与流体流动耦合需要极大计算消耗,工程上应用只需抓住主要物理机理,因此这里采用流体流动近似模拟方法[12]。多孔介质中的流体流动被假设成在相邻孔隙中管道中的流动。控制域是相邻的4个骨架颗粒形成的,每个颗粒中心是四面体的一个顶点,岩石孔隙用球形颗粒间的孔隙代替。
管道流量采用Poiseuille定律来计算
| $q = \dfrac{{ka^3 \Delta p}}{{8L}}$ | (4) |
式中:
为了计算图 5所示骨架颗粒间非规则孔喉截面所代表的管道内径,采用Bryant提出的基于稳态纳维-斯托克斯方程的非规则截面有效流动半径近似计算方法[13]
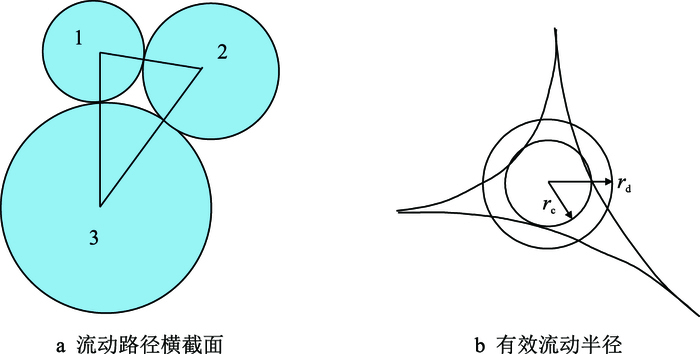 |
| 图5 三维DEM流动管道横截面示意图 Fig. 5 Diagram of cross-section for a 3D flow channel in DEM |
| $r_{\rm{e}} = ({{r_{\rm{c}} + r_{\rm{d}} }})/{2}$ | (5) |
式中:
计算每个时间步每个控制域流入或流出的流量
| $\Delta p_{\rm{t}} = \dfrac{{K_{\rm{f}} }}{{V_{\rm{d}} }}\left( {\Sigma q\Delta t - \Delta V_{\rm{d}} } \right)$ | (6) |
式中:
一个骨架颗粒上受到流体的作用力为
| $\mathit{\boldsymbol{F}}_i = p\mathit{\boldsymbol{n}}_i s$ | (7) |
式中:
流入或流出一个控制域的流量为
| $q = N\dfrac{{ka^3 \Delta p_{\rm{p}} }}{{\bar L}}$ | (8) |
式中:
流体流动产生压力差为
| $\Delta p_{\rm{r}} = \dfrac{{K_{\rm{f}} qt}}{{V_{\rm{d}} }}$ | (9) |
当该压力变化小于初始压力波动时,得到流体计算的最优时间步
| $\Delta t < \dfrac{{\bar LV_{\rm{d}} }}{{NK_{\rm{f}} ka^3 }}$ | (10) |
利用上面建立的Antler天然岩芯骨架颗粒模型对达西流进行模拟验证,生成流体孔隙网络如图 6所示,颗粒直径为0.5 mm,管道内径为0.141 9 mm,控制域直径为0.262 0 mm,在进行达西流验证的时候忽略岩石的力学耦合作用。在模型的两端压力差为0.685 MPa,时间步长设为0.000 1 s,计算的孔隙压力剖面如图 7a所示,可以看出初始时刻压力主要集中在底部,随着模拟时间增加孔隙压力逐渐向线性分布靠拢,这说明在不考虑应力和渗透率的相互作用下,压力分布符合达西定律所描述的线性关系。模拟结束时压力分布如图 7b所示,图中孔隙压力大小与绿色圆圈半径成正比,可以看出孔隙压力沿注入端到产出端呈逐渐减小的趋势。
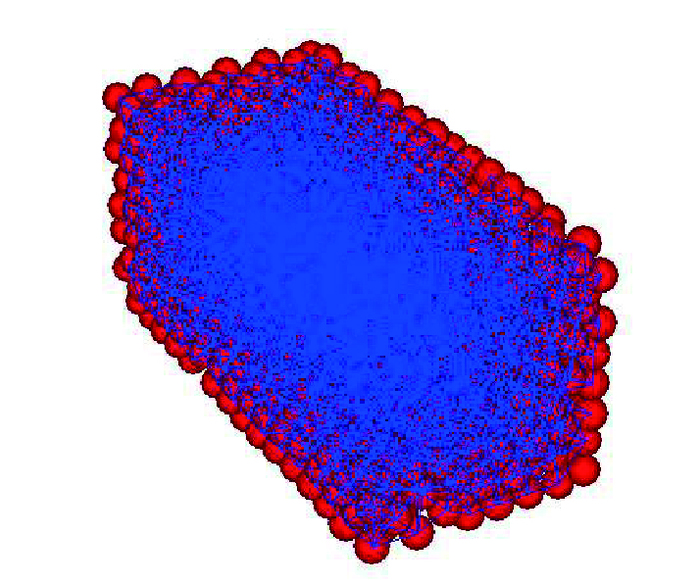 |
| 图6 DEM生成的Antler砂岩流体域网络 Fig. 6 The flow domain network of Antler core model generaged by DEM |
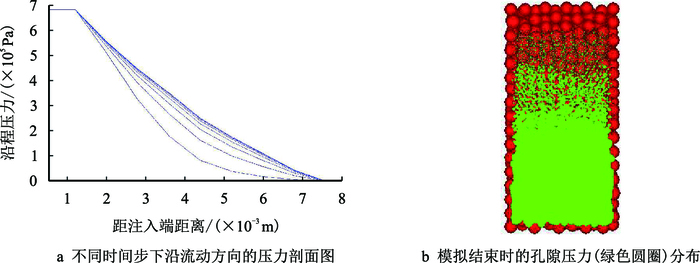 |
| 图7 DEM模拟结果 Fig. 7 DEM simulation results |
悬浮颗粒的力学性质会影响与地层骨架颗粒的相互作用,从而影响地层渗透率的大小。本研究所使用的部分悬浮颗粒性质参数参考Mondol的研究[13],地层流体和悬浮颗粒参数如表 2所示,渗透率通过利用Carman-Kozeny方程来估计[14]
| 表2 地层流体和悬浮颗粒参数 Table 2 The parameters for formation fluid and particle gel |
| $K = \dfrac{{\phi ^3 }}{{c\left( {1 - \phi } \right)^2 S^2 }}$ | (11) |
式中:
利用DEM来模拟悬浮颗粒的侵入过程,假设开始时颗粒滤饼静止在流入端一侧,模型建立如图 8a所示,图中一侧的小颗粒为悬浮颗粒,在岩样的一侧预先生成。在水动力作用下,颗粒开始从一侧进入到多孔介质中的孔隙中。所有的悬浮颗粒具有相同的初始速度,初始速度为流体流速。悬浮颗粒进入地层后开始与骨架颗粒发生接触,悬浮颗粒与骨架颗粒的接触力改变了悬浮颗粒的运动方向和速度大小,进而使得流体对悬浮颗粒的拖拽力发生变化,一定计算时间步循环后,悬浮颗粒的拖拽力根据新的速度而更新。颗粒侵入的中间状态如图 8b所示,颗粒在多孔介质右侧已侵入区域分散在各个孔隙中,类似的颗粒侵入的最后状态如图 8c所示,颗粒滞留在多孔介质中从而对地层造成一定的伤害。
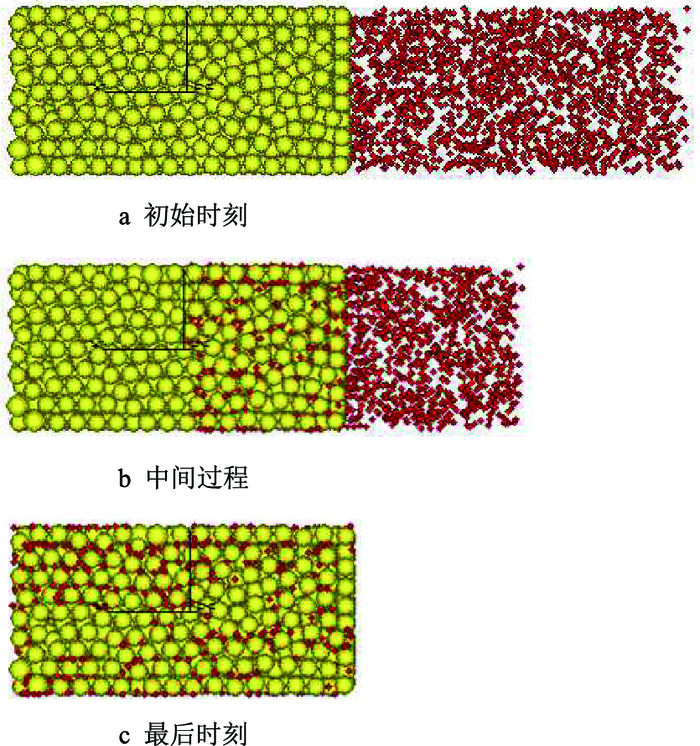 |
| 图8 DEM悬浮颗粒侵入模拟过程 Fig. 8 Simulation process for suspended particles invasion in DEM |
悬浮颗粒在多孔介质中滞留会减小孔隙尺寸,从而对流动造成损伤。利用颗粒侵入结果分析地层伤害的影响程度,对孔隙度和渗透率的下降进行定量分析,表 3展示了不同颗粒粒径比和初始孔隙度的模拟方案及其模拟结果。
| 表3 模拟方案参数和颗粒侵入结果 Table 3 The parameters of simulation cases and results of particle invasion |
方案1~3和方案4~6是分别设置颗粒粒径比(骨架颗粒粒径与侵入颗粒粒径之比)为3,5,10的模拟方案,可以分别计算出匹配度(侵入颗粒粒径与喉道直径之比),根据前人天然岩芯中悬浮颗粒堵塞室内实验结果,本文中6个方案的匹配度均小于0.777时,所以部分颗粒能够贯穿岩芯,发生贯穿性堵塞[15]。此时对比不同模拟方案结果可以看出:
当侵入颗粒粒径越小的时候,岩芯侵入后孔隙度降低程度越大,这是因为颗粒粒径越小越容易进入到孔隙中,从而对地层孔隙度造成更大的降低,对于孔隙度大的岩芯,孔隙度降低幅度更大,这是由于孔隙度大的岩芯的孔隙尺寸相应增大,有利于颗粒运移到地层深部造成封堵。利用Carman-Kozeny方程计算颗粒侵入后导致的渗透率降低,可以看出当颗粒粒径越小所造成的渗透率下降幅度越大,造成的地层伤害也越大。
从表 3中对比颗粒粒径比相同初始孔隙度不同的方案(比如方案1和方案4),初始孔隙度大的岩芯的颗粒侵入后孔隙度降低值要大于初始孔隙度小的岩芯,可以看出初始孔隙度大的岩芯的渗透率下降幅度也大,这说明相同粒径的侵入颗粒对孔隙度大的地层伤害程度更严重,也从侧面说明了悬浮颗粒对高孔高渗地层会造成更严重的产能下降,因此在防止地层伤害注水方案设计时要针对具体地层的孔隙度和渗透率情况严格控制悬浮颗粒的粒径和浓度。
5 结论(1) 建立了悬浮颗粒在多孔介质中运移的微观孔隙模拟方法,通过拟合微观力学参数生成了Antler天然砂岩骨架颗粒模型,利用颗粒离散元方法建立了骨架颗粒流体孔隙网络模拟方法,通过达西线性流验证了骨架颗粒流体耦合的正确性。
(2) 在分析颗粒受力基础上,建立了侵入颗粒与流体相互作用模型和侵入颗粒与骨架颗粒相互作用模型,悬浮颗粒侵入多孔介质的模拟结果表明在发生贯穿性堵塞时粒径小的颗粒造成更大地层伤害,初始孔隙度大的岩芯的渗透率降低幅度较大。
| [1] | CIVAN F. Formation damage mechanisms and their phenomenological modeling:an overview[C]. SPE 107857, 2007. doi:10.2118/107857-MS |
| [2] | TODD A C, SOMERVILLE J E, SCOTT G. The application of depth of formation damage measurements in predicting water injectivity decline[C]. SPE 12498, 1984. doi:10.2118/12498-MS |
| [3] | PAUTZ J F, CROCKER M E, WALTON C G. Relating water quality and formation permeability to loss of injectivity[C]. SPE 18888, 1989. doi:10.2118/18888-MS |
| [4] |
张金波, 于远成, 唐善法, 等. 注入水水质地层伤害因素室内研究[J].
江汉石油学院学报, 2001, 23(2): 53–55.
ZHANG Jinbo, YU Yuancheng, TANG Shanfa, et al. Laboratory study of formation damage factors caused by injected water quality[J]. Journal of Jianghan Petroleum Institute, 2001, 23(2): 53–55. doi: 10.3969/j.issn.1000-9752.2001.02.023 |
| [5] |
刘想平, 侯立朋. 油田注入水中固体颗粒对地层伤害的数学模型[J].
江汉石油学院学报, 1995, 17(2): 69–73.
LIU Xiangping, HOU Lipeng. A mathematical model for simulating formation damage due to solid particles invasion during water injection[J]. Journal of Jianghan Petroleum Institute, 1995, 17(2): 69–73. |
| [6] | SHUTONG P, SHARMA M M. A model for predicting injectivity decline in water-injection wells[J]. SPE Formation Evaluation, 1997, 12(3): 194–201. doi: 10.2118/28489-PA |
| [7] | ALTOE F, BEDRIKOVETSKI P, SANTOS A G, et al. Role of dispersion in injectivity impairment:mathematical and laboratory study[C]. SPE 90083, 2004. doi:10.2118/90083-MS |
| [8] | YUN S K, WHITTLE A J. Filtration in a porous granular medium:1. simulation of pore-scale particle deposition and clogging[J]. Transport in Porous Media, 2006, 65(1): 53–87. doi: 10.1007/s11242-005-6087-2 |
| [9] | SHI Xiaoyan, PRODANOVIC M, HOLDER J, et al. Permeability estimation of damaged formations near wellbore[C]. SPE 146833, 2011. doi:10.2118/146833-MS |
| [10] | WANG H, KRISHNAN G R, ROEGIERS J C, et al. Behavior of natural and remolded antler sandstone:sample preparation and grain crushing aspects[C]. SPE 95-0127, 1995. |
| [11] | CUNDALL P A, STRACK O D. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47–65. doi: 10.1680/geot.1979.29.1.47 |
| [12] | SHIMIZU Y. Fluid coupling in PFC2D and PFC3D[C]//Numerical Modeling in Micromechanics Via Particle Methods Proc of the 2nd International PFC Symposium, Kyoto, Japan, 2004. |
| [13] | MONDOL N H, JAHREN J, BJØRLYKKE K, et al. Elastic properties of clay minerals[J]. The Leading Edge, 2008, 27(6): 758–770. doi: 10.1190/1.2944161 |
| [14] | SHI X, PRODANOVIĆM, HOLDER J, et al. Coupled solid and fluid mechanics modeling of formation damage near wellbore[J]. Journal of Petroleum Science & Engineering, 2013, 112(3): 88–96. doi: 10.1016/j.petrol.2013.10.011 |
| [15] |
罗莉涛, 廖广志, 张玉, 等. 注水中悬浮颗粒堵塞储层的影响因素分析[J].
科技导报, 2014, 32(36): 69–74.
LUO Litao, LIAO Guangzhi, ZHANG Yu, et al. Influencing factors of reservoir plugging caused by suspended particles in injected water[J]. Science & Technology Review, 2014, 32(36): 69–74. doi: 10.3981/j.issn.1000-7857.2014.36.011 |
 2017, Vol. 39
2017, Vol. 39


