2. 中国地质大学“非常规天然气地质评价与开发工程”北京市重点实验室, 北京 海淀 100083;
3. 中国石油西南油气田分公司川西北气矿, 四川 江油 621700;
4. 北京恺标技术发展有限公司, 北京 海淀 100083
2. Beijing Key Laboratory of Unconventional Natural Gas Geology Evaluation and Development Engineering, China University of Geosciences, Haidian, Beijing 100083, China;
3. Northwest of Sichuan Gas Field, Southwest Oil & Gasfield Company, PetroChina, Jiangyou, Sichuan 621700, China;
4. Beijing Kaibiao Technology Development Co. Ltd., Haidian, Beijing 100083, China
20世纪90年代以来,计算机硬件的革命性发展使得大规模统计计算成为可能[1-10],以GSLib的出现为标志[1],基于变差函数的地质统计学储层建模算法趋于成熟并被广泛应用于油气藏储层建模领域[11-15]。然而,克里金算法不能满足所有建模要求,尤其是对高弯曲度的曲流河储层模拟时,克里金算法显露出了其无法描述复杂地质体轮廓的缺陷。基于对象的储层建模通过定义地质体的空间展布特征参数定义一个地质对象,使用硬数据作为模型的约束条件模拟地质体的空间形态,再在地质体中使用克里金算法“填充”地质属性[16]。该方法可以得到清晰的地质体空间展布形态,但在条件化已知地质数据时,地质体越大,已知数据在条件模拟时就越难被真实再现。
从储层建模的实现过程看,除了序贯模拟步骤相同外,多点地质统计学(MPS)是一种新的建模方法。MPS的算法思想形成于20世纪90年代初,由于算法对内存与CPU的要求较高,直到2002年,第一个真正有意义的MPS算法SNESIM才得以实现并被广泛应用[17-24]。由SNESIM衍生的算法可以分为2个大类:(1) 以SNESIM为代表的、基于像素的模拟算法[25];(2) 基于样式的模拟算法,根据其统计、分类样式的不同,又可以分为以SIMPAT为代表的直接使用样式的算法[26]、以FILTERSIM为代表的基于对样式过滤分类的模拟算法[27-28]和基于样式多维空间距离的模拟算法等3类[29]。
1 基于变差函数的地质统计学储层建模 1.1 变差函数与实验变差函数基于变差函数的地质统计学建模将储层属性视为区域化随机变量,通过统计已知空间位置上的随机变量对之间的相关关系,建立线性插值模型,进而模拟出空间未知数据位置上的随机变量值。随机变量对的相关关系通过变差函数定义
| $\gamma (h) = \dfrac{1}{2}\textrm{Var}[Z(x)-Z(x + h)]$ | (1) |
式中:
γ (h)-变差函数;
Var-方差函数;
h-空间距离;
x-空间位置;
Z-区域化变量。
为了获得稳定的变差函数,在数学上可以不考虑随机变量的协方差函数,只要随机变量的矢量增量的协方差函数存在且平稳,就可以计算实验变差函数
| $\gamma ^{*}(h) = \dfrac{1}{2 \times N(h)}\sum\limits_{i = 1}^{N(h)} {{[Z({x_i} + h)-Z({x_i})]}^2}$ | (2) |
式中:
γ*(h)-实验变差函数;
N(h)-在空间距离为h的区域化随机变量对应的数量。
1.2 基于变差函数的模拟算法以当前模拟点为中心,假设在搜索范围内搜索到n个已知数据,估值模型为
| ${Y^*}(u) = \sum\limits_{\beta = 1}^n {{\lambda _\beta } \cdot Y({u_\beta })}$ | (3) |
式中:
Y*(u)-中心点u的估计值;
Y(uβ)-已知数据;
λβ
uβ-空间位置。
使用最小二乘法,建立相应的简单克里金方程组
| $\sum\limits_{\beta =1}^{n}{{{\lambda }_{\beta }}C({{u}_{\alpha }}-{{u}_{\beta }})=C(u-{{u}_{\alpha }}),\quad \quad \alpha =1,2,}\cdots ,n$ | (4) |
式中:
uα-空间位置;
C(uα-uβ)-已知数据点uα与uβ的方差;
C(u-uα)-待估点u与已知数据点uα的方差。
方差可通过计算两点距离,从实验变差函数中读取。模拟算法的步骤为:(1) 将数据转化为标准正态分布,统计数据点对,建立实验变差函数;(2) 对研究区内未知数据点定义随机模拟路径,定义搜索范围;(3) 对每个模拟点,按搜索范围搜索已知数据点,建立克里金方程组,解方程组得到估计参数;(4) 计算克里金估计方差;(5) 重复第(3) 步,直到所有的未知数据点都被模拟完成,最后,将模拟数据分布转换回原来的分布。
1.3 基于变差函数的储层建模Deutsch[24]认为,如果不能明确确定这个均值的趋势,最好不用漂移克里金算法。Patriarche等[30]对几种不同的克里金算法进行了比较,并给出了成功使用漂移算法的模拟实例。Machuca-Mory等[31]通过距离权重建立局部平稳变差函数的方法解决非平稳现象。模拟数据要求统计数据充足才能支持该算法,否则,由于计算距离及插值引入的误差将带来不稳定的模拟结果。地质体的延展方向通常是多变的,基于变差函数的建模算法无法在理论上解决这个问题。有学者将研究区划分为多个区域,在不同的区域使用不同的变差函数来解决这个问题,但区域划分非常困难,且这样的模拟结果会造成边界处的不连续。
2 基于对象的储层建模克里金估值是一种最优无偏估计,但变差函数统计的是空间两点间的差值,因此无法体现复杂地质体的空间形态。为了能够更好地描述地质体空间展布特征,提出了基于对象的地质统计学储层模拟方法。该方法的核心思想是将地质体形态以现有数据为约束条件,进行参数化,从而通过这些参数来模拟地质体的空间展布形态。得到地质体的空间展布轮廓之后,在地质体空间内部,使用基于变差函数的建模方法模拟地质体的属性。
描述地质体形态的参数根据具体模拟对象不同而不同,对于砂质河道充填的模拟参数需要包括河道的总体延伸方位角、河道宽度、河道弯曲度及宽厚比等参数。对于复杂的叠覆河道复合体,先模拟级别较高的大型河道,然后采用层次分析法在大河道体内部模拟小型河道。在算法上,基于对象的建模算法实际上是基于变差函数算法的扩展,将基于变差函数的建模空间限制在地质体空间内部。
基于对象的方法可以模拟出具有光滑边界的地质体,但当条件数据较多时,地质体参数与这些条件数据就会变得难以调和,从而产生与条件数据相矛盾的模拟结果。一般在地质体的大小超过条件数据平均距离时,矛盾较为明显。基于对象的建模注重地质体的形态特征,模拟结果的数据分布与条件数据的分布较难保持一致,因此,在实际应用中较少使用。
3 MPS建模 3.1 基本概念 3.1.1 训练图像训练图像是一个二维或三维的图像。任何MPS算法都使用至少一个训练图像。所有目标实现中的数据均来源于对训练图像的统计。训练图像要足够大,以满足研究对象所有可能样式的分布都能与训练图像一致。
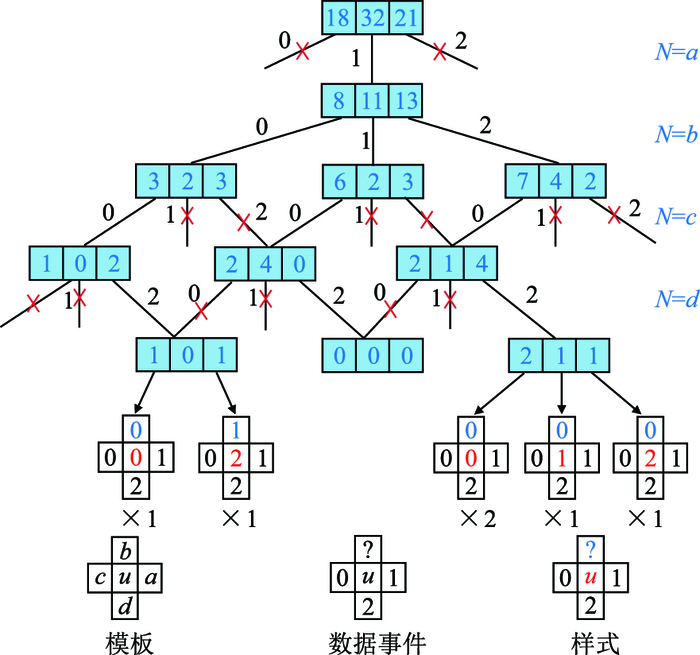
3.1.2 模板、样式与数据事件模板可以是任意形状的二维或三维的、与位置无关的空间区域,一般远小于训练图像(图 1)。MPS算法并没有规定模板的形状或轮廓,完全可以根据实际需要定义任意形状的模板。
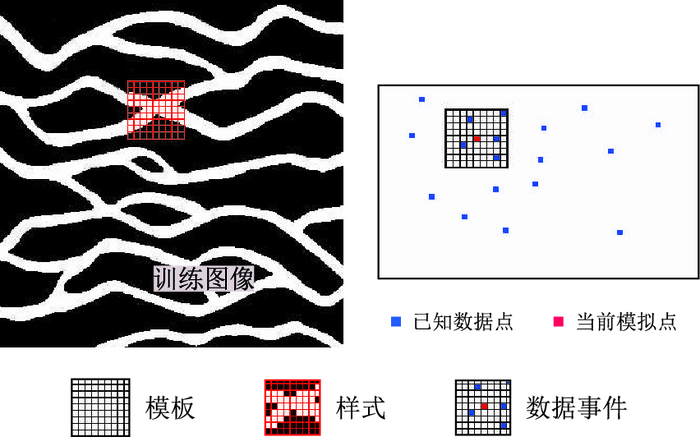 |
| 图1 二维模板、样式与数据事件图解 Fig. 1 Graphic of two-dimensional template, style and data events |
用模板在训练图像中搜索,得到所有与模板大小相同的二维或三维“块”,称为样式。每个样式都表征其中心点处的数据属性。数据事件是在对目的区域中未知数据点进行模拟时,以该点为中心,在模板所定义的范围内可获得的、已知数据所构成的矢量数据集。
3.2 MPS算法 3.2.1 基于像素的算法SNESIM算法是基于像素算法的代表。Strebelle[25]提出了使用中间网格及优化模板大小的方法来提高该算法的模拟速度,但没有就内存问题给出切实可行的解决方案。Straubhaar等[26, 27]将样式以数据事件中某类随机变量值的个数为依据有序排列,或直接以数据事件中某类随机变量的可能取值次序排列,将搜索树替换为链表。这将减少了内存的使用量,同时,使用链表可以灵活进行并行计算,但在搜索过程中对CPU的要求明显高于SNESIM算法。为解决计算速度问题,多线程并行是提高计算效率的一个有效途径[32]。
SNESIM算法首先在训练图像中按定义好的模板提取所有样式并组织在搜索树中,在模拟计算前,为每一级网格结构建立树结构。假设模板有N个网格节点,模拟离散型的属性共有M种可能取值,则树结构最多有N层,每一个节点至少由M个整数构成,分别代表M个属性值的样式数目(图 2),全部节点C实际上存储的就是样式分布。
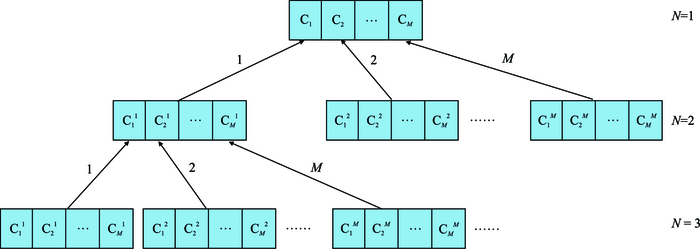 |
| 图2 SNESIM搜索树结构 Fig. 2 The structure of SNESIM search tree |
搜索树的层对应的节点在模板中以距离中心点的远近来组织,M越小,距离中心点越近(图 3),图 3中相同颜色的节点具有与中心点相同的距离。
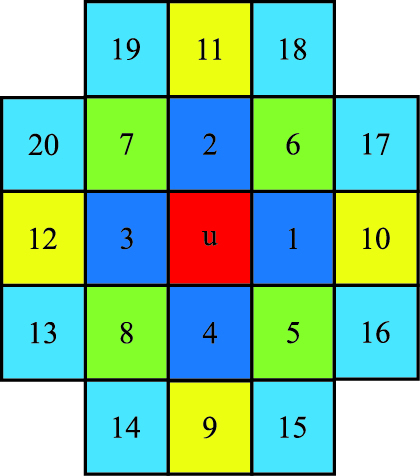 |
| 图3 搜索树节点组织示意图 Fig. 3 The node organization diagram of search tree |
为了模拟不同尺度的储层形态特征,SNESIM使用多重网格模拟,二维与三维网格相邻的、较低级别网格的尺寸是较高级别的22倍或23倍(图 4),网格级别越低,提取的样式所反映的地质体形态越大。
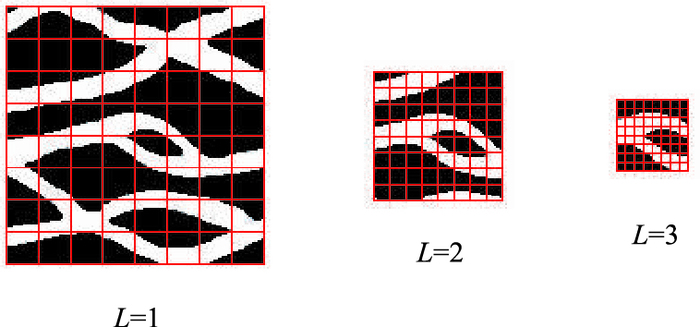 |
| 图4 3个二维网格在同一训练图像中同一点提取的样式差异 Fig. 4 Style differences of three 2D grids extracted at the same point in the same training image |
模拟过程如下:(1) 建立所有待模拟网格的随机路径;(2) 按模板大小沿随机路径构造数据事件;(3) 在树中搜索与数据事件匹配的样式分布;(4) 将抽取的数据作为已知数据再重复步骤(2),直到完成所有未知数据点的模拟。
图 5给出了模拟离散型随机变量的一个数据事件过程,离散型随机变量的属性有3种类型,分别用0、1、2表示,模板由4个临近数据以及中心数据点构成,除中心点外的数据点排列次序,按逆时针方向依次组织为a、b、c、d,数据事件位置a对应属性1,位置b没有与之对应的属性,位置c对应属性0,位置d对应属性2。每个节点由3个分别代表属性0、1、2出现频数的整数构成,是数据事件的分布。红色的叉代表该分支不被搜索。
 |
| 图5 搜索树的搜索过程示意图 Fig. 5 Search process diagram of search tree |
从位置a开始搜索,位置a在数据事件中对应的属性为1,因此,在搜索树上不必搜索$N=a$分支的对应属性为0和2的分支,而只搜索数据属性为1的分支。由于位置b没有已知数据,要搜索该节点下的所有3个分支。位置c对应的属性为0,在$N=c$的分支下,只搜索属性为0的子分支。位置d对应的属性为2,在$N=d$的分支下只搜索属性为2的子分支。最后,得到3个该数据事件的分布,分别为1、0、1;0、0、0和2、1、1。累计得到的数据事件分布为3、1、2,即:对应该数据的事件,有
基于样式的MPS算法与SNESIM算法最大的差别就是不再使用搜索树,具有代表性的算法有直接模拟法SIMPAT[33]、过滤模拟法FILTERSIM[34, 35]和MDS[36]。
样式与样式或样式与数据事件的距离指的是两个样式或样式与数据事件之间的相似程度,最简单的距离定义为
| $\left\{ \begin{array}{*{35}{l}} {{L}_{\text{PP}}}=\frac{1}{{{n}_{\text{P}}}}\sum\limits_{i=0}^{{{n}_{\text{P}}}}{|{{P}^{\text{A}}}({{r}_{i}})-{{P}^{\text{B}}}({{r}_{i}})|} \\ {{L}_{\text{DP}}}=\frac{1}{c}\sum\limits_{i=0}^{c}{|{{D}^{\text{A}}}({{r}_{i}})-{{P}^{\text{B}}}({{r}_{i}})|} \\ \end{array} \right.$ | (5) |
式中:LPP-样式间距离;
r-矢量的空间位置;
nP-样式中的数据总数;
PA-样式A中第i个位置上的值;
PB-样式B中第i个位置上的值;
DA-数据事件A在第i个位置上的值;
LDP-数据事件与样式的距离;
c-数据事件中已知数据个数。
(1) SIMPAT算法
SIMPAT算法既不建立搜索树,也不存储样式分布。对于整个训练图像,除边缘部分外,每一个点位置就代表了一个样式,不对样式进行归类统计。模拟步骤如下:① 确定模板大小,建立模拟随机路径,并定义一个最小距离;② 沿随机路径提取数据事件,遍历训练图像,计算每一个样式与该数据事件的距离,找到最小的距离,如找不到满足条件的样式,就放宽最小距离限制,如果找到多个最小距离相同的样式,随机抽取一个;③ 将样式直接“贴”到数据事件上,如果是条件模拟,则在条件数据点上保持条件数据,将该模拟点作为后续模拟的已知数据;④ 重复步骤②,直到所有节点的模拟完成。
模拟时,所有的CPU均集中在计算数据事件与样式的距离上,使用多重模板可提高运算速度。使用特定的数据事件遍历样式时,首先采用较粗模板对应的样式计算数据事件与该样式的距离,而在提取距离最近的样式时,提取双重模板的数据(图 6)。
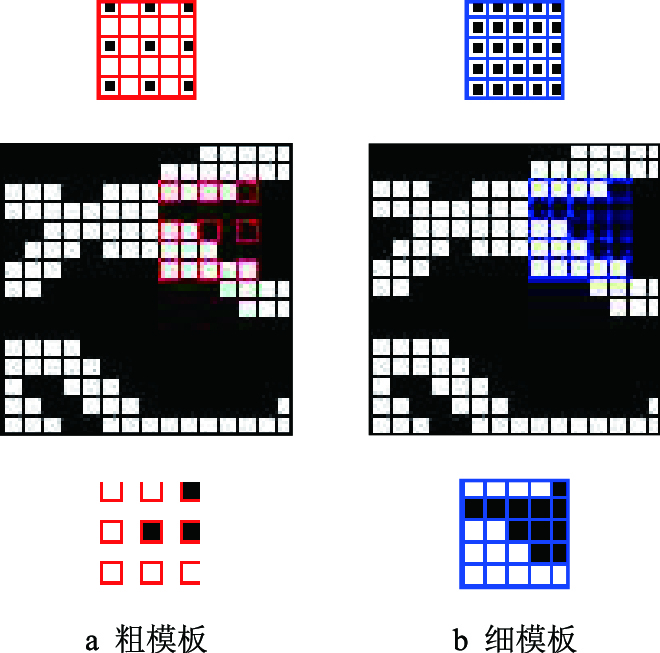 |
| 图6 使用双重模板提取样式示意图 Fig. 6 Style sketch for the extraction using dual template |
(2) FILTERSIM算法
模拟前,FILTERSIM算法先使用过滤器过滤TI,每一个过滤器都会得到一个相应的训练图像。设有L个过滤图像,以模板为窗口过滤TI,所有过滤器分别对每一个维度(二维或三维)训练图像进行过滤,得到过滤后的训练图像(二维为2L个,三维为3L个)。根据每一个过滤图像的值域,设置分类标准。进行模拟时,按网格级别从粗到细进行模拟:① 按照网格级别确定模板,定义模拟随机路径;② 提取样式,对样式进行分类,相似的样式归到一个类别,每一类别最终均由一个类似于标识号的名为样式原型的样式来代表,该样式原型即为每一个类别中所有样式的平均;③ 按照该路径提取相应网格的数据事件,计算数据事件与每一个样式原型的距离,找到最小距离的那个样式类别,从中提取一个样式作为模拟点位置的数据,将提取的样式中心部分(可以由用户定义这个中心范围,这个范围要小于模板)作为模拟结果数据,不再更新,样式中心以外的数据暂时存放到相应位置,在后续的模拟时需要更新;④ 重复步骤③,直到完成所有路径上节点的模拟;⑤ 重复步骤①,直到所有最小网格的模拟完成。
FILTERSIM算法的关键在于过滤训练图像与分类样式。过滤器的作用是区分不同的样式,Zhang等提出了线性过滤器[34],3个线性过滤器分别为
| $\left\{ \begin{array}{*{35}{l}} {{f}_{\text{ave}}}({{m}_{i}})=1-\frac{|{{m}_{i}}|}{m} \\ {{f}_{\text{grad}}}({{m}_{i}})=\frac{{{m}_{i}}}{m} \\ {{f}_{\text{curv}}}({{m}_{i}})=2\frac{|{{m}_{i}}|}{m}-1 \\ \end{array} \right.$ | (6) |
式中:fave-平均过滤器;
fgrad-梯度过滤器;
fcurv-曲度过滤器;
m-模板网格点的个数。
使用每一个过滤器对训练图像过滤后,得到了与过滤器同等数目的新图像,确定每一个图像的极值,将这些图像的极值均分为K段,这样就可以确定分类单元,如果有L个过滤器,那么这样的单元就有KL个,每个单元的对应过滤器所过滤的训练图像值域范围都是唯一的,将训练图像上对应的样式存放到这样的单元中,完成样式分类。
这类线性过滤器在进行训练图像过滤时速度快,但较为粗糙,因此,Wu等[27-28]提出使用K-mean聚类算法来完成无监督的学习分类,该算法分类效果比线性过滤好,但比较耗时。
(3) 基于距离的MDS算法
Honarkhah与Caers提出了一种新的样式分类模拟方法[29]。将两个不同样式之间的相似性距离定义为
| ${d_{\rm{E}}}\left[\right.p_{\rm{T}}^{m}(u), p_{\rm{T}}^{n}(u)\left. \right] = \sum\limits_{i = 1}^{nT} {\left[\right.p_{\rm{T}}^{m}({h_i})-p_{\rm{T}}^{n}({h_i}){{\left. \right]}^2}}$ | (7) |
式中:p-模板函数;
在FILTERSIM算法中,使用过滤训练样本的方法来分类样式,MDS算法则使用样式间的距离对样式进行分类。为了尽可能保留距离的精度,同时减少需要计算距离的节点数,MDS算法采用了两步法:首先,使用主成分分析对样式中对应的模板节点按计算样式距离时的贡献程度进行排序,即根据它们的特征值大小排序
对于任意固定值q(nT>q>0),将特征值分为两个总体:
| ${{l}_{q}}(q)=-q\lg \left( \frac{1}{\sqrt{2\pi \sigma _{1}^{2}}} \right)\sum\limits_{i=1}^{q}{\frac{({{d}_{i}}-{{\mu }_{1}})}{2\sigma _{1}^{2}}}+(q-nT)\lg \left( \frac{1}{\sqrt{2\pi \sigma _{2}^{2}}} \right)\sum\limits_{i=q+1}^{nT}{\frac{({{d}_{i}}-{{\mu }_{2}})}{2\sigma _{2}^{2}}}$ | (8) |
函数
使用K-mean算法分类样式前,使用了高斯核函数对距离进行了强制转换,进而对转换后的距离进行线性分类。Honarkhah与Caers用实例证明了这样的分类算法优于过滤分类算法。另一种使用基于距离的模拟算法是计算不同实现之间的相似性[37],该算法使用后处理的方式,通过优选构造一个新的实现。
3.3 MPS的适用性对训练图像的基本要求是训练图像所反映的地质特征与所要模拟的储层特征一致。除SIMPAT算法外,其他算法对训练图像的要求更高,就是对应每一个模板,从训练图像上统计出来的不同样式的分布要与目标储层的相应样式一致,训练图像必须能够近似反映待模拟数据的总体分布。
关于训练图像的潜在要求或假设包括:(1) 训练图像中每一种待模拟的元素所占的比例与实际地层中对应的元素所占比例近似相同;(2) 训练图像中地质对象的形态虽然不可能与实际地层相同,但必须一致,如河道弯曲的河道位置可以不同,但弯曲度和尺度等需要保持一致;(3) 训练图像中地质体的延展方向需要与实际地层一致。其中,(2) 与(3) 事实上就是很多学者所讨论的平稳性问题。
在MPS算方法中,对模板大小的假设是模板能够捕获训练图像中的所有属性特征。Strebelle讨论了基于SNESIM算法多级(3级)网格下模板尺寸的优化算法[32],通过逐渐增加数据事件中节点数目在搜索树中获取数据事件的模拟结果的方法来确定模板的最佳大小。这一计算过程是有缺陷的,这是由于对应一个数据事件的每一种可能模拟结果可能是各不相同的,只模拟一个结果是不科学的,如果全部模拟,可能会导致不确定性且非常耗时。使用同一训练图像、同一模板,不同网格级别以得到不同的模板尺寸,这种方法的难点在于如何将条件数据置于较粗网格节点上。
4 地质统计学储层建模发展方向储层建模的目的是使用已知数据和可能的辅助数据,尽可能准确地反映待模拟储层属性特征的空间分布。两点地质统计学目前已经较成熟[38-40],但仍难以在实际应用中有新的突破。MPS由于以其灵活的数据统计与分类方法,可以在更多领域为地质工作提供有效的研究手段。
4.1 薄非渗透性夹层模拟Huysmans等[41]提出了使用MPS模拟砂岩体中的薄泥质夹层。该方法具有较强的现实意义,这是由于在开发过程中,储层内部的非均质性主要是由这类泥质薄夹层造成的。
4.2 集成生产数据生产数据可以反映储层的连续性,如示踪剂追踪数据。使用MPS算法进行条件模拟时,往往缺少对储层井间连续性的考虑。Renard等[13]在使用改进的SNESIM算法,利用注采数据模拟井间储层的连续性。这一算法避免了井间连续的储层在模拟实现中被切断。
4.3 分形特征模拟Mariethoz等[19]在研究图像比例关系时,使用SNESIM算法获得了不同比例尺下的清晰图像。Mariethoz等认为,图像的边界类似于地图中的海岸线,在不同比例尺下具有自相关性。在油气藏中,裂缝的分布与发育特征可能存在自相关性,根据该研究,可以使用MPS算法研究裂缝的分布特征。
5 结论(1) 地质统计学算法在储层建模中起到了重要作用。从两点地质统计学到MPS,准确表征地下储层的属性特征是其发展的内在动力。
(2) 地质统计学储层建模主要分为基于变差函数的建模、基于对象的建模和MPS建模。基于变差函数的建模易于条件化已知数据,模拟实现的随机变量分布也易于与条件数据保持一致,但基于变差函数的建模仅考虑矢量点对之间的统计关系,因此,无法模拟出复杂地质体的形态特征;基于对象的建模可以得到较好的地质体形态,但较难实现条件化已知数据;MPS力求在条件模拟时既易于条件化硬数据,又能较好地反映地质体的形态特征。\par (3) 地质统计学模拟对算法平稳性要求较高,基于变差函数的模拟可以通过漂移算法改进随机变量的平稳性;MPS可以使用与位置相关的辅助训练样本作为额外约束条件,从而实现非平稳模拟的效果。
(4) MPS在薄非渗透性夹层模拟、集成生产数据模拟井间储层连续性及裂缝分形特征的随机模拟中会有更多潜力。
| [1] | DEUTSCH C V, JOURNEL A G. GSLIB:Geostatistical software library and user's guide[M]. y: Oxford University Press, 1998. |
| [2] | TAHMASEBI P, HEZARKHANI A, SAHIMI M. Multiple-point geostatistical modeling based on the cross-correlation functions[J]. Computational Geosciences, 2012, 16(3): 779–797. doi: 10.1007/s10596-012-9287-1 |
| [3] | de IACO S, MAGGIO S. Validation techniques for geological patterns simulations based on variogram and multiple-point statistics[J]. Mathematical Geosciences, 2011, 43(4): 483–500. doi: 10.1007/s11004-011-9326-9 |
| [4] | CHENG C, YU W, BAI X. The research on method of interlayer modeling based on seismic inversion and petrophysical facies[J]. Petroleum, 2016, 2(1): 20–25. doi: 10.-1016/j.petlm.2015.10.001 |
| [5] | JAFARPOUR B, KHODABAKHSHI M. A probability conditioning method (PCM) for nonlinear flow data integration into multipoint statistical Facies simulation[J]. Mathematical Geosciences, 2011, 43(2): 133–164. doi: 10.-1007/s11004-011-9316-y |
| [6] |
石石, 高立祥, 刘莉莉, 等. 苏里格气田苏6加密井区有效储层地质建模[J].
西南石油大学学报(自然科学版), 2015, 37(1): 44–50.
SHI Shi, GAO Lixiang, LIU Lili, et al. Geological modeling of effective sandstone reservoir of the Su-6 infilling drilling pilot in Sulige Gas Field[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 44–50. doi: 10.11885/j.issn.1674-5086.2013.06.08.06 |
| [7] |
李保华, 邓世彪, 陈永权, 等. 塔里木盆地柯坪地区下寒武统台缘相白云岩储层建模[J].
天然气地球科学, 2015, 26(7): 1233–1244.
LI Baohua, DENG Shibiao, CHEN Yongquan, et al. The reservoir modeling of platform margin dolostone of Xiaoerblak Formation, Lower Cambrian, Kalpin Area, Tarim Basin[J]. Natural Gas Geoscience, 2015, 26(7): 1233–1244. doi: 10.11764/j.issn.1672-1926.2015.07.1233 |
| [8] |
计秉玉, 赵国忠, 王曙光, 等. 沉积相控制油藏建模技术[J].
石油学报, 2006, 27(S1): 111–114.
JI Bingyu, ZHAO Guozhong, WANG Shuguang, et al. Geologic modeling technique of oil reservoir based on sedimentary facies control[J]. Acta Petrolei Sinica, 2006, 27(S1): 111–114. doi: 10.7623/syxb2006S1022 |
| [9] |
刘超, 谢传礼, 李宇鹏, 等. 利用虚拟井提高相控随机建模中地质约束的原理和方法[J].
天然气地球科学, 2015, 26(4): 616–624.
LIU Chao, XIE Chuanli, LI Yupeng, et al. The principle and method to enhance geological constraint by inserting virtual wells in facies controlling stochastic reservoir modeling[J]. Natural Gas Geoscience, 2015, 26(4): 616–624. doi: 10.11764/j.issn.1672-1926.2015.04.0616 |
| [10] |
邓西里, 李顺明, 孔垂显, 等. 新疆金龙2油田裂缝性火山岩油藏地质建模方法[J].
西南石油大学学报(自然科学版), 2016, 38(4): 37–47.
DENG Xili, LI Shunming, KONG Chuixian, et al. Geological modeling of fractured volcanic reservoir in Jinlong 2 Oilfield, Xinjiang[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(4): 37–47. doi: 10.11885/j.issn.1674-5086.2014.11.17.01 |
| [11] | THORE P, SHTUKA A, LECOUR M, et al. Structural uncertainties:Determination, management, and applications[J]. Geophysics, 2002, 67(3): 840–852. doi: 10.-1190/1.1484528 |
| [12] | RASTEGARNIA M, SANATI A, JAVANI D. A comparative study of 3D FZI and electrofacies modeling using seismic attribute analysis and neural network technique:A case study of Cheshmeh-Khosh Oil field in Iran[J]. Petroleum, 2016, 2(3): 225–235. doi: 10.1016/j.petlm.2016.-06.005 |
| [13] | RENARD P, STRAUBHAAR J, CAERS J, et al. Conditioning facies simulations with connectivity data[J]. Mathematical Geosciences, 2011, 43(8): 879–903. doi: 10.-1007/s11004-011-9363-4 |
| [14] |
谌卓恒, OSADETZK G. 西加拿大沉积盆地Cardium组致密油资源评价[J].
石油勘探与开发, 2013, 40(3): 320–328.
CHEN Zhuoheng, OSADETZ K G. An assessment of tight oil resource potential in the Upper Cretaceous Cardium Formation, western Canada Sedimentary Basin[J]. Petroleum Exploration and Development, 2013, 40(3): 320–328. doi: 10.11698/PED.2013.03.08 |
| [15] | SCHEIDT C, CAERS J. Representing spatial uncertainty using distances and kernels[J]. Mathematical Geosciences, 2009, 41(4): 397–419. doi: 10.1007/s11004-008-9186-0 |
| [16] | BERTONCELLO A, SUN T, LI Hongmei, et al. Conditioning surface-based geological models to well and thickness data[J]. Mathematical Geosciences, 2013, 45(7): 873–893. doi: 10.1007/s11004-013-9455-4 |
| [17] |
邹拓, 徐芳. 复杂断块油田开发后期精细地质建模技术对策[J].
西南石油大学学报(自然科学版), 2015, 37(4): 35–40.
ZOU Tuo, XU Fang. Technical strategy for fine geological modeling in later development stage of complex faultblock oilfield[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(4): 35–40. doi: 10.11885/j.issn.1674-5086.2013.12.08.03 |
| [18] | CAERS J. History matching under training-image based geological model constraints[J]. SPE Journal, 2003, 8(3): 218–226. doi: 10.2118/74716-PA |
| [19] | MARIETHOZ G, RENARD P, STRAUBHAAR J. Extrapolating the fractal characteristics of an image using scale-invariant multiple-point statistics[J]. Mathematical Geosciences, 2011, 43(7): 783–797. doi: 10.1007/s11004-011-9362-5 |
| [20] | MIRANDA H, DE MIRANDA M S. Combining robustness with efficiency in the estimation of the variogram[J]. Mathematical Geosciences, 2011, 43(3): 363–377. doi: 10.1007/s11004-010-9308-3 |
| [21] | BACHMAIER M, BACKES M. Variogram or semivariogram? Variance or semivariance? Allan variance or introducing a new term?[J]. Mathematical Geosciences, 2011, 43(6): 735–740. doi: 10.1007/s11004-011-9348-3 |
| [22] | FRITZ J, NEUWEILER I, NOWAK W. Application of FFT-based algorithms for large-scale universal kriging problems[J]. Mathematical Geosciences, 2009, 41(5): 509–533. doi: 10.1007/s11004-009-9220-x |
| [23] | YAMAMOTO J K. Correcting the smoothing effect of ordinary kriging estimates[J]. Mathematical Geology, 2005, 37(1): 69–94. doi: 10.1007/s11004-005-8748-7 |
| [24] | DEUTSCH C V. Geostatistical reservoir modeling[M]. New York: Oxford University Press, 2002. |
| [25] | STREBELLE S. Conditional simulation of complex geological structures using multiple-point statistics[J]. Mathematical Geology, 2002, 34(1): 1–21. doi: 10.1023/A:-1014009426274 |
| [26] | STRAUBHAAR J, RENARD P, MARIETHOZ G, et al. An improved parallel multiple-point algorithm using a list approach[J]. Mathematical Geosciences, 2011, 43(3): 305–328. doi: 10.1007/s11004-011-9328-7 |
| [27] | WU Jianbing, BOUCHER A, ZHANG Tuanfeng. A SGeMS code for pattern simulation of continuous and categorical variables:FILTERSIM[J]. Computers & Geosciences, 2008, 34(12): 1863–1876. doi: 10.1016/j.cageo.-2007.08.008 |
| [28] | WU Jianbing, ZHANG Tuanfeng, JOURNEL A. Fast FILTERSIM simulation with score-based distance[J]. Mathematical Geosciences, 2008, 40(7): 773–788. doi: 10.1007/-s11004-008-9157-5 |
| [29] | HONARKHAH M, CAERS J. Stochastic simulation of patterns using distance-based pattern modeling[J]. Mathematical Geosciences, 2010, 42(5): 487–517. doi: 10.1007/-s11004-008-9157-5 |
| [30] | PATRIARCHE D, CASTRO M C, GOOVAERTS P. Estimating regional hydraulic conductivity fields-a comparative study of geostatistical methods[J]. Mathematical Geology, 2005, 37(6): 587–613. doi: 10.1007/s11004-005-7308-5 |
| [31] | MACHUCA-MORY D F, DEUTSCH C V. Non-stationary geostatistical modeling based on distance weighted statistics and distributions[J]. Mathematical Geosciences, 2013, 45(1): 31–48. doi: 10.1007/s11004-012-9428-z |
| [32] | STREBELLE S, CAVELIUS C. Solving speed and memory issues in multiple-point statistics simulation program SNESIM[J]. Mathematical Geosciences, 2014, 46(2): 171–186. doi: 10.1007/s11004-013-9489-7 |
| [33] | ARPAT G B, CAERS J. Conditional simulation with patterns[J]. Mathematical Geology, 2007, 39(2): 177–203. doi: 10.1007/s11004-006-9075-3 |
| [34] | STRAUBHAAR J, WALGENWITZ A, RENARD P. Parallel multiple-point statistics algorithm based on list and tree structures[J]. Mathematical Geosciences, 2013, 45(2): 131–147. doi: 10.1007/s11004-012-9437-y |
| [35] | ZHANG Tuanfeng, SWITZER P, JOURNEL A. Filterbased classification of training image patterns for spatial simulation[J]. Mathematical Geology, 2006, 38(1): 63–80. doi: 10.1007/s11004-008-9154-8 |
| [36] | SUZUKI S, CAERS J. A distance-based prior model parameterization for constraining solutions of spatial inverse problems[J]. Mathematical Geosciences, 2008, 40(4): 445–469. doi: 10.1007/s11004-008-9154-8 |
| [37] | LIU Yuhong. Using the Snesim program for multiple-point statistical simulation[J]. Computers & Geosciences, 2006, 32(10): 1544–1563. doi: 10.1016/j.cageo.2006.02.008 |
| [38] |
崔勇, 栾瑞乐, 赵澄林. 辽河油田欧利坨子地区火山岩储集层特征及有利储集层预测[J].
石油勘探与开发, 2000, 27(5): 47–49.
CUI Yong, LUAN Ruile, ZHAO Chenglin. Volcanic rock reservoir characteristics and prediction in Oulituozi Region, Liaohe Basin[J]. Petroleum Exploration and Development, 2000, 27(5): 47–49. |
| [39] |
程超, 吴东昊, 桑琴, 等. 基于蚂蚁体的"相"控地质建模[J].
西安石油大学学报(自然科学版), 2011, 26(3): 21–25.
CHENG Chao, WU Donghao, SANG Qin, et al. Faciescontrolled geological modeling based on ant body[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2011, 26(3): 21–25. |
| [40] |
刘克奇, 郝雪峰. 成熟探区精细地质评价技术研究进展[J].
西南石油大学学报(自然科学版), 2015, 37(1): 11–18.
LIU Keqi, HAO Xuefeng. Advances in intensive geological evaluation methods of the mature exploration areas[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 11–18. doi: 10.11885/j.-issn.1674-5086.2013.01.05.01 |
| [41] | HUYSMANS M, DASSARGUES A. Direct multiplepoint geostatistical simulation of edge properties for modeling thin irregularly shaped surfaces[J]. Mathematical Geosciences, 2011, 43(5): 521–536. doi: 10.1007/s11004-011-9336-7 |
 2017, Vol. 39
2017, Vol. 39


