2. 西华大学流体及动力机械教育部重点实验室, 四川 成都 600300;
3. “煤矿灾害动力学与控制”国家重点实验室·重庆大学, 重庆 沙坪坝 400044
2. MOE Key Laboratory of Fluid and Power Machinery, Xihua University, Chengdu, Sichuan 600300, China;
3. State Key Laboratory of Disaster Dynamics and Control of Coal Mine, Chongqing University, Shapingba, Chongqing 400044, China
由于水平井能够提高单井油气产量和采收率,现已越来越多地用于常规油气、页岩气的开采。随着技术的发展,1 000 m及其以上长度水平段的水平井数量越来越多,为低效低渗、难开采油田和海油陆采提供了有效的技术手段[1-6],水平段越长,井眼轨迹控制的难度越大且摩阻问题越突出[7-12]。然而在水平井水平段的钻进过程中,由于地层结构特点(不均匀地层、倾斜构造等)、钻具振动、钻头侧向力[13]、近钻头岩屑沉积[14]和钻井操作等因素将导致实钻水平段井眼轨迹发生三维空间上的连续小幅偏斜波动[15],该种偏斜虽不会引起实钻井眼轨迹的严重偏离,但会改变钻柱与井眼的接触形态及其自身的弯曲形态。由于现有测井方法多采用每10 m或30 m间隔测点,表征井眼弯曲至少需4个测点(40~120 m),而反演井眼轨迹时,该长度足以忽略掉井眼轨迹的小幅偏斜波动,这也导致了对该种现象及其对摩阻影响的相关研究很少。此外,现有钻柱力学研究过程中,也多忽略掉该种偏斜现象,将钻柱与井壁作连续接触处理,而实际钻柱具有一定的刚度,其与连续小幅偏斜井眼间的接触规律及其对最钻进摩阻的影响需要深入的研究,以对水平井钻进摩阻的准确预测及控制提供指导。
DB25-1井是中国石油化工股份有限公司东北油气分公司的一口中深层水平井,该井水平段长744 m,水平段井眼直径216 mm,井眼扩大率为15.6%,采用每30 m和每1 m测点反演获得的部分水平段实钻井眼轨迹对比图如图 1(
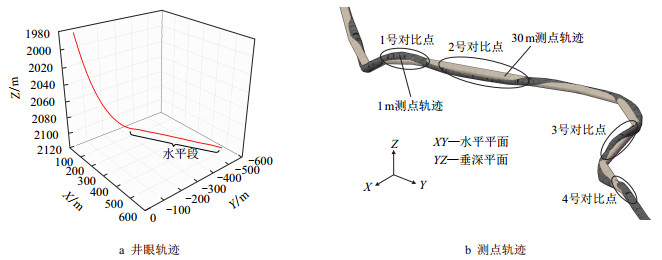 |
| 图1 DB25-1井不同距离测点条件下的井眼轨迹对比图 Fig. 1 The comparison between different logging methods of DB25-1 |
从图 1中可以看出,每1 m测点反映出了井眼轨迹偏斜波动的形态。如1号对比点所示,每30 m测点反演的井眼轨迹近似为直线,而实际轨迹存在上凸,即井眼轨迹在井斜平面内向上发生了偏斜波动。同理,2~4号对比点也反映出在井斜平面内的偏斜波动。鉴于此,本文采用理论分析与仿真相结合的方法,针对水平段井眼轨迹在井斜平面内连续偏斜波动条件下的钻柱与井壁接触形态及其影响因素,以及对摩阻的影响展开了研究。
1 静态条件下钻柱悬跨分析通常认为,水平段钻柱在重力作用下会紧压下井壁并与之形成连续接触,并将其作为现有解析法求解钻柱力学相关问题的前提假设条件,但由于钻柱具有一定的刚度,水平段钻柱与实钻连续偏斜波动井眼的连续接触可能被破坏,形成钻柱仅与波动井眼两峰顶接触的“悬跨”接触现象。钻柱在自身重力、钻井流体介质以及轴向力和扭矩联合作用下发生弯曲,当弯曲位移大于井眼轨迹的偏斜波动幅值时,钻柱便与井壁发生接触。因此,根据井眼尺寸、井径扩大率、管柱结构(钻井管柱、套管柱)和钻井流体介质,便可获得特定井眼尺寸条件下,发生悬跨接触的最大临界跨距以及偏斜幅值。井斜平面内水平段钻柱与偏斜波动井眼发生悬跨接触的相对形位状态如图 2所示。
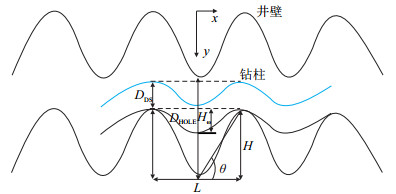 |
| 图2 管柱与峰顶接触时的形位关系 Fig. 2 The position of drillstring and hole well with deflection |
图 2中虚线为未发生弯曲的钻柱初始位置,细实线为发生弯曲后的钻柱。从图 2中可以看出,钻柱与偏斜波动井眼形成悬跨接触的临界条件为:(1) 井眼直径与其轨迹偏斜幅值的差大于钻柱直径与其弯曲位移的差;(2) 井眼轨迹偏斜幅值大于钻柱的弯曲位移,即
| $ \left\{ {\begin{array}{*{20}{l}} {{D_{{\rm{HOLE}}}} - H \geqslant {D_{{\rm{DS}}}} - {H_\omega }}\\ {H - {H_\omega } \geqslant 0} \end{array}} \right. $ | (1) |
式中:
偏斜幅值与最大临界跨距关系为
| $ H = \dfrac{L}{2}\tan \theta $ | (2) |
式中:
钻柱与井壁的悬跨接触简化为简支状态下的等截面圆环直梁,其在重力、轴向力和扭矩作用下的受力示意图如图 3所示。
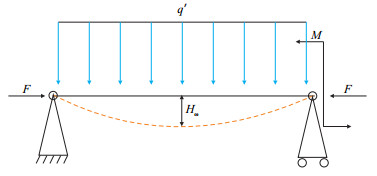 |
| 图3 钻柱静态条件下的弯曲位移分析 Fig. 3 The bend analysis of drillstring in static state |
根据弯曲梁理论,当且仅考虑钻柱自重影响时,其最大弯曲位移发生在二分之一跨距位置处,其值为
| $ {H_\omega } = - \dfrac{{5q'{l^4}}}{{384EI}} $ | (3) |
式中:
| $ q' = \left( {1 - \dfrac{{{\rho _{{\rm{FLUID}}}}}}{{{\rho _{{\rm{DS}}}}}}} \right){\rho _{{\rm{DS}}}}{\rm{g}}l\left( {{A_{{\rm{DS}}}} - {{A'}_{{\rm{DS}}}}} \right) $ | (4) |
式中:
g—重力加速度,g = 9.8 m/s
联合式(1)~式(4) 得偏斜波动井眼轨迹在某跨距上的可偏斜角,进而判断静态钻柱与井壁接触与否,其表达式如式(5) 所示,当可偏斜角为0°时,表明钻柱与井壁接触。
| $ \dfrac{1}{2}L\tan \theta \leqslant - \dfrac{{5{L^5}{\rm{g}}}}{{384EI}}\left( {{\rho _{{\rm{DS}}}} - {\rho _{{\rm{FLUID}}}}} \right)\left( {{A_{{\rm{DS}}}} - {{A'}_{{\rm{DS}}}}} \right) + \\[5pt] {\kern 40pt} {D_{{\rm{HOLE}}}} - {D_{{\rm{DS}}}} $ | (5) |
以DB25-1井为例进行分析,水平井段钻进多采用普通钻杆与加重钻杆组成的钻井管柱串,普通钻柱外径127.0 mm,内径108.0 mm,名义重量240 N/m,加重钻柱外径127.0 mm,内径76.2 mm,名义重量为724 N/m,弹性模量210 GPa。由此计算不同跨距条件下静态钻柱弯曲位移与相应的井眼轨迹可偏斜角度,计算结果如表 1所示。
| 表1 常压与超压型页岩气藏特征对比 Table 1 The characteristics comparison between common pressure and overpressure shale gas reservoirs |
从表 1中可知,当普通钻柱的跨距超过15.3 m时,悬跨钻柱的中间点将与下井壁发生接触,加重钻柱时为17.9 m,说明管柱的抗弯模量越大允许的最大临界跨距越长。案例井中2号、3号对比点处的悬跨长度均超过了15.3 m,因此静态钻柱在一个悬跨范围内存在多点接触(两峰顶加中间点),此时钻柱与井壁的接触方式不同于仅考虑钻柱接头支撑的情况,也不同于现有解析法求解钻柱力学相关问题中普遍采用的钻柱与井眼下壁连续接触的前提假设条件,根据接触面形貌特征及真实接触面积对摩擦力影响的相关理论[16-17],钻柱与井眼的悬跨接触将降低现有钻柱力学研究方法假设条件的合理性,导致计算误差的出现。
2 动态条件下钻柱悬跨分析在实际钻进过程中,水平段钻柱受轴向力、扭矩和重力的共同作用,采用弹性力学叠加原理分析该种情况下水平段钻柱在井斜平面内的弯曲变形,将其分解为扭矩载荷与重力和轴向力共同作用产生的弯曲位移和,扭矩载荷条件下的简支梁弯曲位移公式
| $ {H_\omega } = - \frac{{Mx}}{{6lEI}}\left( {{l^2} - {x^2}} \right), \;\;\;\;(x = l/2, l/\sqrt 3 ) $ | (6) |
式中:
重力和轴向力共同作用下的简支梁弯曲位移公式为[18]
| $ \left\{ \begin{array}{l} {H_\omega } = {C_1}x\sin \lambda - {C_2}x\cos \lambda - \\{\kern40pt}{C_3}\left( {\dfrac{{{x^2}}}{2} - \dfrac{{lx}}{2} - \dfrac{1}{{{\lambda ^2}}}} \right)\\ \lambda = \sqrt {{F}/{EI}} \\[5pt] {C_1} = \dfrac{{mEI}}{{{F^2}l\sin \lambda }}\left( {l\cos\lambda - 1} \right)\\[6pt] {C_2} = {{mEI}}/{{{F^2}}}\\[5pt] {C_3} = {m}/{F} \end{array} \right. $ | (17) |
式中:
以加重钻杆为例进行计算,在80 kN轴向力和8 kN·m扭矩作用下的弯曲位移及总的弯曲位移如图 4所示。从图中可以看出,轴向力和重力对钻柱弯曲位移的影响最大,占总弯曲位移贡献量的90%,钻柱弯曲位移最大位置仍为二分之一跨距位置处。
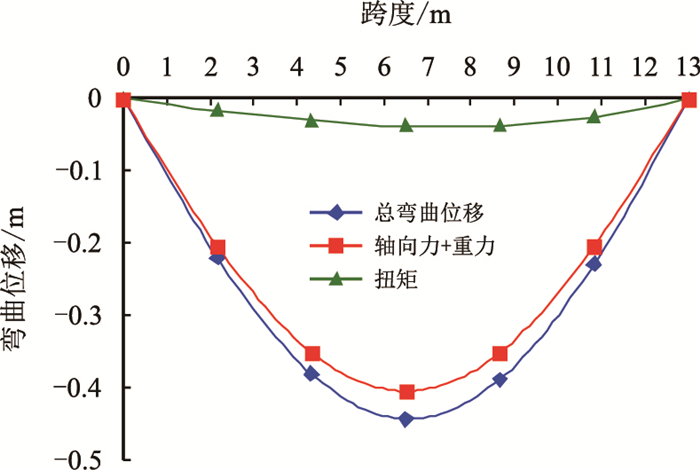 |
| 图4 加重钻柱13 m跨度的弯曲位移 Fig. 4 The bending displacement of HWDP when span is 13 m |
井眼轨迹出现连续偏斜波动反映了实钻过程中环境因素对钻进作业的影响,是一种不可避免的现象,为了保障后期管柱串和套管的顺利下入,必须将井眼轨迹的偏斜控制在合理的范围内,假设连续偏斜井眼轨迹在一个偏斜单元长度上近似为一圆弧,由此可计算出该段井眼轨迹的曲率。对于水平井钻井管柱串,加重钻杆由于壁厚增加,其抗弯模量大于普通钻杆,由此重点考虑加重钻杆的通过曲率要求,此外还需考虑该井段所用套管的通过曲率要求。
DB25-1井选用的加重钻杆材料为S135级钢,屈服强度取931 MPa,所用外径177.8 mm套管材料为N80钢,屈服强度取758 MPa,通过式(8) 计算该井钻井管柱串和套管顺利下入所要求的最大偏斜波动井眼轨迹曲率,计算公式为[19]
| $ {K_{{\rm{Limit - lowing}}}} = \dfrac{{1719}}{{E{D}{k_1}{k_2}}}200{Y_{\rm{\rho }}} $ | (8) |
式中:
计算得DB25-1井钻井管柱串和套管的最大通过曲率为0.755和0.439 °/(30 m),于是,该井眼轨迹偏斜的曲率上限为0.439 °/(30 m),并以此为曲率约束,由式(6) 和式(7) 计算得钻井过程中,不同轴向力和扭矩对钻井管柱串发生悬跨接触的偏斜井眼轨迹最大临界跨距的影响,如图 5和图 6所示。
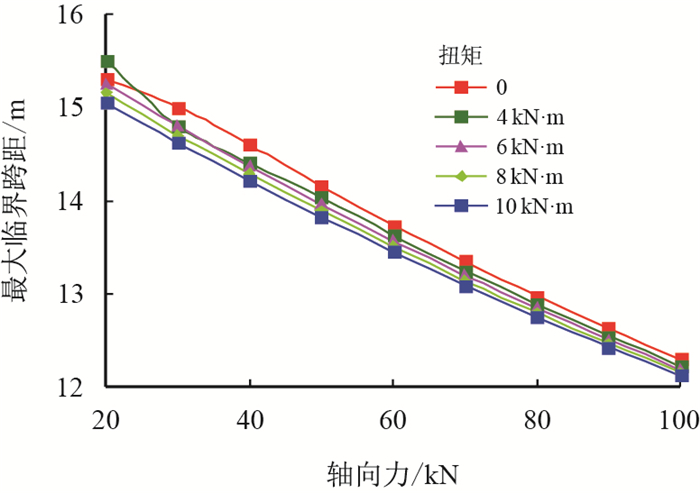 |
| 图5 轴向力对最大临界跨距的影响 Fig. 5 The influence of axil force on the critical span length |
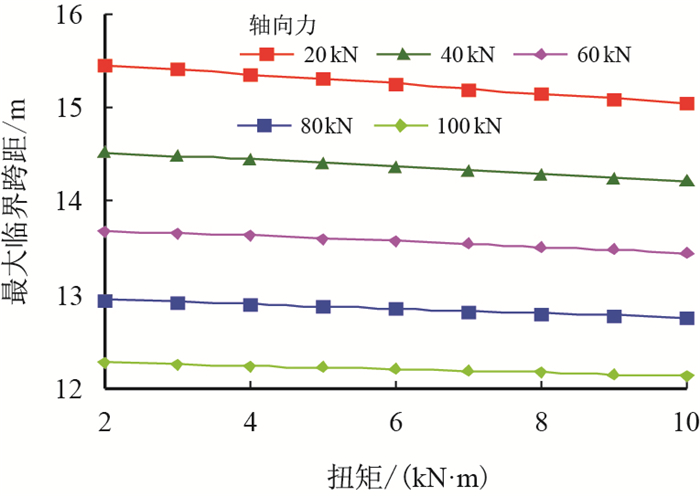 |
| 图6 扭矩对最大临界跨距的影响 Fig. 6 The influence of torque on the critical span length |
从图 5可见,随着轴向力的增加,案例井发生悬跨接触的最大临界跨距近似呈线性减小趋势,扭矩8 kN·m、轴向力20 kN时,最大临界跨距为15.15 m即是1.62根钻杆长度,而当轴向力增至100 kN时则缩短至12.16 m,降幅达22.2%。
图 6反映了扭矩对最大临界跨距的影响,从图 6中可以看出,随着扭矩的增加,最大临界跨距仅出现了小幅下降,从降幅可以看出,扭矩对临界跨距影响较小,降幅最大出现在轴向力20 kN时,当扭矩从2 kN·m增加至10 kN·m时,跨距也仅缩短了0.41 m,降幅为2.7%。而当轴向力为100 kN时,扭矩引起的降幅更小,为0.14 m,降幅仅1.1%。
综上所述,轴向力为最大临界跨距的主要影响因素,由此可以推断,由于摩阻导致的水平段轴向力沿程损耗,使得近钻头钻柱被施加的轴向力减小,同等条件下更易发生钻柱悬跨现象。此外,最大临界跨距从另一个层面反映了对井眼轨迹的控制要求,临界跨距越小则表示对井眼轨迹控制的要求越严格,甚至需调整现有钻井工艺与井下钻具组合,下入专用的井眼轨迹控制工具等,导致钻井成本的增加。
3 井眼轨迹偏斜对钻进摩阻的影响以DB25-1井水平段钻进用钻具组合、作业参数等为背景资料,采用仿真方法,建立部分水平段悬跨接触三维钻进模型,分析井眼轨迹偏斜对摩阻的影响。水平段模型段长80 m,钻井液密度取1 300kg/m
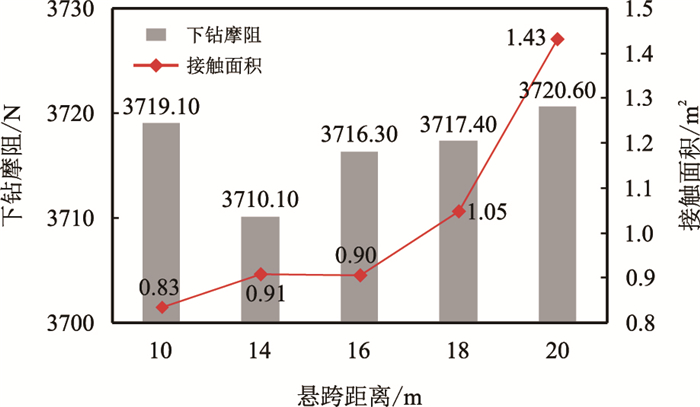 |
| 图7 不同悬跨距离对下钻摩阻的影响 Fig. 7 The effect of span length on drag when lowering |
从图 7中可以看出,除跨距10 m外,摩阻与接触面积均随悬跨距离的增加而增加,当跨距为14和16 m时,由于该跨距条件下,钻柱与井壁仍为悬跨接触,因此接触面积几乎没有增加。当跨距为18 m时,通过前面的计算可知,此时钻柱的理论弯曲位移大于井眼轨迹的偏斜幅值,钻柱在二分之一悬跨位置处与井壁发生了接触,形成了第三处接触。当跨距增大至20 m时,钻柱的理论弯曲位移继续增大,但在钻柱重力与井壁限制共同作用下表现为第三处接触处的面积增大,进而使得整体接触面积增大。摩阻虽表现出增加的趋势,但增幅并不明显,出现该种趋势的原因是由于模拟下钻时未考虑岩屑沉积、钻具台阶面以及不规则井壁的影响,仅仅反映了井眼轨迹偏斜引起的钻柱悬跨对摩阻的影响。
当轴向力为80 kN,转速60 r/min时,跨距对钻进摩阻的影响如图 8所示。从图 8中可以看出,钻进摩阻整体表现为随跨距增加而增加的趋势,从跨距10 m时的7.9 kN增至16 m时的8.4 kN,随后趋于稳定并在20 m时达到最大值8.6 kN,增幅达8.9%。然而钻柱与井壁的接触面积却随跨距的变化表现出先增大再减小后趋于稳定的趋势,根据不同跨距条件下钻柱的弯曲程度大致分为两种情况,当跨距为钻柱弯曲位移较小的10 m时,钻柱与井壁接触面积最小仅3.7 m
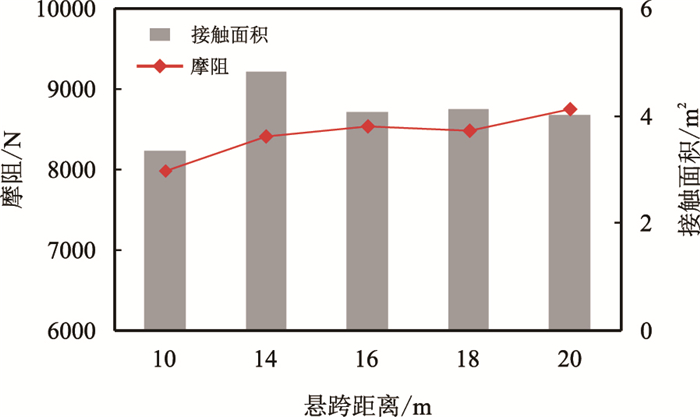 |
| 图8 不同悬跨距离对钻进摩阻的影响 Fig. 8 The effect of span length on drag when drilling |
(1) 水平段钻柱与连续小幅偏斜波动井眼间易形成悬跨接触现象,管柱的抗弯模量越大,相同条件下偏斜井眼轨迹的最大临界跨距越大,对于水平井钻进作业而言,即对井眼轨迹控制的要求相对较小。当实际跨距大于最大临界跨距时,钻柱将与井壁将产生多点接触,其接触方式不同于仅考虑钻柱接头支撑的情形,更不同于现有解析法求解钻柱力学相关问题中普遍采用的钻柱与井眼下壁连续接触的假设条件。
(2) 外加载荷中,轴向力和重力对悬跨钻柱弯曲位移的影响最大,占总弯曲位移贡献量的90%,钻柱最大弯曲位移处仍为1/2跨距位置。随着轴向力的增加,悬跨接触偏斜井眼轨迹的最大临界跨距近似成线性减小趋势,扭矩对临界跨距影响较小。
(3) 实钻井眼轨迹小幅值偏斜导致的钻柱悬跨改变了钻柱与井壁的接触方式,减小了钻柱与井壁的接触面积并对钻进摩阻影响较大。因此,为提高水平井的钻达深度、控制钻进摩阻,有必要采用有限元方法深入研究水平井眼轨迹连续小幅偏斜波动对全井摩阻的影响。
| [1] |
马凤清, 牛洪波, 崔海林. 胜利油田长水平段水平井钻井技术现状与认识[J].
中外能源, 2013, 18(5): 51–55.
MA Fengqing, NIU Hongbo, CUI Hailin. Present situation and recognition on horizontal drilling technology for long horizontal section well in Shengli Oilfield[J]. Sino-Global Energy, 2013, 18(5): 51–55. |
| [2] |
常海军, 李祥群, 张娜, 等. 河南油田页岩油长水平段水平井钻井实践[J].
复杂油气藏, 2013, 6(2): 66–70.
ChANG Haijun, LI Xiangqun, ZhANG Na, et al. Drilling practice of long horizontal section well in shale oil reservoir in Henan Oilfield[J]. Complex Hydrocarbon Reservoirs, 2013, 6(2): 66–70. doi: 10.3969/j.issn.1674-4667.-2013.02.021 |
| [3] |
徐云龙. 川西浅层气藏小井眼长水平段水平井钻井技术[J].
钻采工艺, 2013, 36(4): 111–113.
XU Yunlong. The technology of horizontal drilling with small hole well in west part of Sichuan[J]. Drilling & Production Technology, 2013, 36(4): 111–113. doi: 10.3969/-J.ISSN.1006-768X.2013.04.35l |
| [4] |
王可仁, 宁金生, 杨碧学. 苏里格气田超长水平段水平井钻井技术[J].
内蒙古石油化工, 2014, 40(20): 95–96.
WANG Keren, NING Jinsheng, YANG Bixue. The long horizontal drilling technology in Sulige Gas Field[J]. Inner Mongulia Petrochemical Industry, 2014, 40(20): 95–96. |
| [5] |
钱峰, 杨立军. 三塘湖致密油长水平段水平井钻井技术[J].
石油钻采工艺, 2014, 36(6): 20–23.
QIAN Feng, YANG Lijun. Drilling technology for horizontal well with long horizontal sectioninSantanghu tight oil reservoir[J]. Oil Drilling & Production Technology, 2014, 36(6): 20–23. doi: 10.13639/j.odpt.2014.06.005 |
| [6] |
田树林. 薄油层水平井钻井技术研究与应用[J].
钻采工艺, 2004, 27(3): 9–11.
TIAN Shulin. Research on horizontal drilling technology and application in oil Sheet[J]. Drilling & Production Technology, 2004, 27(3): 9–11. doi: 10.3969/j.issn.1006-768X.2004.03.003 |
| [7] |
闫铁, 张凤民, 刘维凯, 等. 大位移井钻井极限延伸能力的研究[J].
钻采工艺, 2010, 33(1): 4–7.
YAN Tie, ZHANG Fengmin, LIU Weikai, et al. Mechanical analysis on the limit extended capacity for an extended reach well[J]. Drilling and Production Technology, 2010, 33(1): 4–7. doi: 10.3969/j.issn.1006-768X.2010.01.002 |
| [8] |
王俊良, 陈洪亮, 刘永峰. 大位移井钻具组合设计及摩阻扭矩分析[J].
钻采工艺, 2012, 35(1): 24–26.
WANG Junliang, CHEN Hongliang, LIU Yongfeng. ERD BHA and its drag and torque analysis technology[J]. Drilling and Production Technology, 2012, 35(1): 24–26. doi: 10.3969/J.ISSN.1006-768X.2012.01.08 |
| [9] |
魏殿举. 川西地区中浅水平井钻井难点与对策[J].
钻采工艺, 2015, 38(2): 105–107.
WEI Dianju. Drilling difficulties and countermeasures of shallow horizontal wells in Western Sichuan area[J]. Drilling and Production Technology, 2015, 38(2): 105–107. doi: 10.3969/J.ISSN.1006-768X.2015.02.31 |
| [10] |
王伟, 管志川, 张文哲, 等. 水平井钻柱延伸能力影响因素分析[J].
钻采工艺, 2015, 38(2): 9–13.
WANG Wei, GUAN Zhichuan, ZhANG Wenzhe. Analysis of factors of influencing drill string extending ability in horizontal well drilling[J]. Drilling and Production Technology, 2015, 38(2): 9–13. doi: 10.3969/J.ISSN.1006-768X.2015.02.03 |
| [11] |
陈雷, 杨国彬, 张玮, 等. 委内瑞拉奥里诺克胡宁区块丛式三维水平井安全钻井技术[J].
天然气工业, 2016, 36(8): 100–106.
CHEN Lei, YANG Guobin, ZHANG Wei, et al. Drilling safety technologies for 3D cluster horizontal wells of Junin Block in Orinoco, Venezuela[J]. Natural Gas Industry, 2016, 36(8): 100–106. doi: 10.3787/j.issn.1000-0976.2016.08.014 |
| [12] |
杨玉坤, 翟建明. 四川盆地元坝气田超深水平井井身结构优化与应用技术[J].
天然气工业, 2015, 35(5): 79–84.
YANG Yukun, ZHAI Jianming. Casing program optimization technology for ultra-deep horizontal wells in the Yuanba Gasfield, Sichuan Basin[J]. Natural Gas Industry, 2015, 35(5): 79–84. doi: 10.3787/j.issn.1000-0976.2015.05.012 |
| [13] |
田平, 练章华, 郑建翔, 等. 气体钻水平井稳定器安放位置与井斜控制研究[J].
西南石油大学学报(自然科学版), 2012, 34(3): 163–168.
TIAN Ping, LIAN Zhanghua, ZHENG Jianxiang, et al. Study of stabilizer location and well deviation control mechanism in gas drilling horizontal well[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(3): 163–168. doi: 10.3863/j.issn.1674-5086.2012.03.025 |
| [14] |
杨晓光, 柳贡慧, 李军, 等. 气体钻水平井段环空岩屑床分布规律研究[J].
钻采工艺, 2014, 37(2): 5–7.
YANG Xiaoguang, LIU Gonghui, LI Jun, et al. Distribution laws of annulus cuttings beds of horizontal well in gas drilling[J]. Drilling and Production Technology, 2014, 37(2): 5–7. doi: 10.3969/J.ISSN.1006-768X.2014.02.02 |
| [15] | MENAND S, SELLAMI H. Buckling of tubulars in actual field conditions:SPE annual technical conference and exhibition[C]. San Antonio, Texas, USA 2006. doi:10.-2118/102850-MS |
| [16] |
韩文梅. 岩石摩擦滑动特性及其影响因素分析[D]. 太原: 太原理工大学, 2012.
HAN Wenmei. The study of frictional sliding characters of rocks and its influencing factors[D]. Taiyuan:Taiyuan University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10112-1012381533.htm |
| [17] |
黄平, 赖添茂. 基于真实接触面积的摩擦模型[J].
华南理工大学学报(自然科学版), 2012, 40(10): 109–114.
HUANG Ping, LAI Tianmao. Firiction model based on real contact area[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(10): 109–114. doi: 10.3969/j.issn.1000-565X.2012.10.015 |
| [18] | DYKSTRA M W. Nonlinear drill string dynamics[D]. Tulsa:The University of Tulsa, 1996. |
| [19] |
李增乐. 中浅层水平井井眼轨道优化设计与现场施工[J].
探矿工程:岩土钻掘工程, 2013, 40(10): 43–45.
LI Zengle. Optimized design of trajectory for middleshallow horizontal well and the site construction[J]. Exploration Engineering Media, 2013, 40(10): 43–45. doi: 10.3969/j.issn.1672-7428.2013.10.016 |
 2017, Vol. 39
2017, Vol. 39


