缝洞型碳酸盐岩由于其储层的特殊性,建产方式主要是直接钻遇储层漏失建产,或者通过储层改造建产。位于塔里木盆地塔中北坡的塔X01井钻遇了优质溶蚀缝洞型储层,取芯发现该储层溶蚀孔洞缝发育。由于客观原因,在测试时压力计只能下至距离储层段放空段1 333.88 m的位置。前期漏失泥浆滤液排出严重影响了测试资料质量,这给解释工作带来很大的困难,难以分清曲线特征究竟是受地层影响还是井筒的原因造成。如果将井筒的动力异常现象误解释为地层的特征,就会不可避免地对气井的产能和储层信息做出错误的判断[1。油田实际生产数据表明,利用常规产能评价方法评价的碳酸盐岩气井无阻流量和后续实际配产产量的比值在4~33。一些学者[2-5]都开展了相关的研究,并都提出了各自的解决方法。本文根据现场实际施工工艺,对气水同产井压力测试方法进行分析,提出了适合研究区的流压校正方法,在此基础上,提出利用约束优化算法进行碳酸盐岩气井产能的评价方法。
1 压力异常现象测试管柱中带两支电子存储压力计,深度分别为5 037.7和5 347.97 m。由于压力计距离储层太远,受产水影响,流压和压恢资料都出现了异常。
测试取得了上下两支压力数据见表 1。
| 表1 塔X01井测试流压数据表 Table 1 TX01 flowing pressure testing data tables |
根据表 1数据,按照两支压力计实测的压力计算的压力梯度对应为:0.35,0.31,0.31,0.35,0.42,0.28 MPa/(×100 m),按这个压力梯度折算至井底,会出现静压小于流压的情况,无法进行产能评价。
2 流压资料处理塔里木盆地井深大于6 000 m,造成井深结构复杂,生产时从下往上的流动通道基本都是“裸眼→套管→小油管→大油管”,各种不同内径的流动通道,其临界携液产量不同。按已有研究成果[6-8]认识,对于气水同产的气井,如果产气量小于最小携液产量,井底就会有积液。同时现场受各方面因素影响,压力计很难下到储层深度,如果流压测试不能测到气水界面,就会造成折算的储层流压偏小,因此准确评价气水同产井产能的第一步是评价清楚井筒积液情况。
2.1 井底积液判断 2.1.1 临界携液计算方法优选临界携液计算有球模型、椭球模型、近似球模型和综合模型[9-11]等,基于这些假设模型,不同学者得出了不同的临界携液计算方法(式(1)),临界流速都具有相同的形式,只是系数
| $ u_{\rm{cr}} = a\left[\dfrac{\sigma \left( {{\rho }_{\rm{L}}}-{{\rho }_{\rm{g}}} \right)}{\rho _{\rm{g}}^{2}} \right]^{0.25} $ | (1) |
| 表2 不同临界携液流量模型系数表 Table 2 The coefficient table of critical liquid carrying model |
式中:
利用塔河31口监测积液井气井对以上模型计算方法进行验证,如图 1所示。
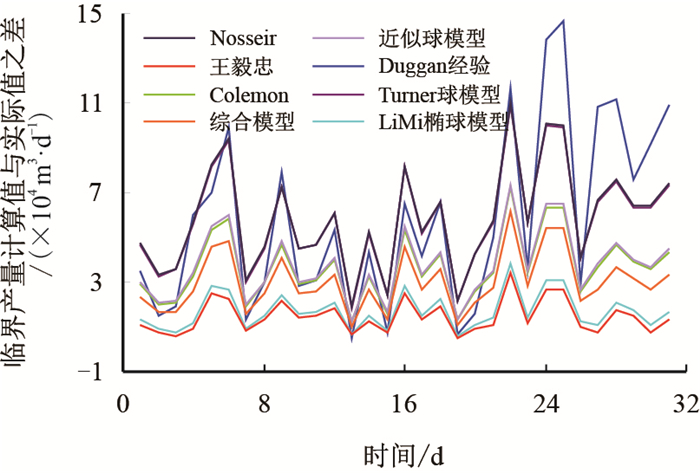 |
| 图1 塔河31口积液井计算图 Fig. 1 The calculation chart of 31 effusion wells in Tahe Oilfield |
计算结果表明,所有模型计算最小临界携液产量都大于实际积液时的生产数据,但是LiMi模型和王毅忠模型最接近实际生产数据,因此优选LiMi模型进行井筒积液判断。
2.1.2 井筒积液判断本次测试的管柱和井筒(油管+套管+裸眼)主要有4种不同内径变化,根据LIMI理论计算不同管柱内径时的临界携液产气量(表 3)。
| 表3 各管柱内径的临界携液计算表 Table 3 The critical liquid carrying calculation sheet of different pipe diameter |
受不同气产量携液能力的影响,随着工作制度的增大,被携带出的泥浆滤液的含量相应增加,表现为流压梯度呈上升趋势(3,5,6,7,9 mm油嘴制度下两支压力计间的流压梯度分别为:0.35,0.31,0.31,0.35,0.42 MPa/(×100 m))。这些不断产出的滤液严重影响了对地层中部流压的折算,造成了随工作制度的增大,折算后的井底流压出现不降反升的反常现象。
2.2.1 流压计算方法优选校正选用目前较为常用的6种井筒两相流压力计算方法:Beggs-Brill(BB)法、Duns-Ros(DR)法、Orkiszewski(OR)法、Mukerjee-Brill(MB)法、无滑脱模型法、SWPI。这里不对这些方法进行详细介绍,可查阅相关文献[9, 12-13]。
利用该井连续井底流压和实际生产数据(日产气、日产水、井口温度、天然气相对密度、水密度、油压)和井底实测流温,对上述6种两相流计算方法进行误差统计(表 4),优选出了适合该井区的4种两相流计算方法。
| 表4 井筒两相流计算方法误差分析统计 Table 4 The error analysis of two phase flow calculation methods |
利用生产气水比对优选出的4种计算方法进行校正,SWPI方法校正计算式为
| $ {{p}_{\rm{wfi}}}=\ln \left( 2.634\times {{10}^{-5}}R+\dfrac{3855.2}{R}-0.090464 \right)+\\{\kern 40pt}{{p}_{\rm{wf}}} $ | (2) |
式中:
MB方法校正计算式
| $ {{p}_{\rm{wfi}}}=\ln \left( 2.761\times {{10}^{-5}}R+\dfrac{1921.6}{R}\rm{+}0.16137 \right)+\\{\kern 40pt}{{p}_{\rm{wf}}} $ | (3) |
无滑脱方法校正计算式
| $ {{p}_{\rm{wfi}}}=\ln \left( 2.222\times {{10}^{-5}}R+\dfrac{982.31}{R}\rm{+0}\rm{.22924} \right)+\\{\kern 40pt}{{p}_{\rm{wf}}} $ | (4) |
DR方法校正计算式
| $ {{p}_{\rm{wfi}}}=\ln \left( 7.089\times {{10}^{-5}}R+\dfrac{10275}{R}\rm{-0}\rm{.94076} \right)+\\{\kern 40pt}{{p}_{\rm{wf}}} $ | (5) |
校正后可以大幅度提高计算精度,见表(5)。
| 表5 4种井筒两相流计算方法校正后误差分析表 Table 5 The error analysis table of the four gas-liquid two phase flow correction calculation |
不同工作制度下井底积液判断见表 6。
| 表6 4个工作制度流压校核数据表 Table 6 The four nozzle checking flow pressure data tables |
在进行流压折算时必须考虑裸眼段的积液。表 6为根据优选的井筒两相流计算方法考虑裸眼段积液计算不同工作制度时井底流压。
3 产能方程推导流体在不同储层中流动可能存在不同的流动阻力,对于常规砂岩气藏一般考虑惯性阻力,用二项式运动方程描述其在地层中流动。但是,碳酸盐岩高温高压气井初始产能极高,流动通道变化多端,利用二项式运动方程描述这样的气藏存在局限。Firoozabadi[14]考虑脉冲阻力,推导出三项式运动方程
| $ \dfrac{{\rm d}p}{{\rm d}r}=\dfrac{\mu }{K}v+\beta \rho {{v}^{2}}+\gamma {{\rho }^{2}}{{v}^{3}} $ | (6) |
式中:
式(6) 中等号右边的第三项代表脉冲阻力项。
气体在流向井筒过程中,在任意流动截面r处的气体流速
| $ v=\dfrac{{{q}_{\rm{g}}}{{B}_{\rm{g}}}}{2\pi rh} $ | (7) |
式中:
将高压下气体密度和体积系数等高压物性计算方程代入到三项式运动方程中,可得
| $ \dfrac{{\rm d}p}{{\rm d}r}=\dfrac{1}{pr}\dfrac{\mu zMT{{p}_{\rm{sc}}}}{2\pi Kh{{T}_{\rm{sc}}}}{{q}_{\rm{g}}}+\dfrac{1}{p{{r}^{2}}}\dfrac{\beta zMTp_{\rm{sc}}^{2}}{4{{\pi }^{2}}{{h}^{2}}{\rm R}T_{\rm{sc}}^{2}}q_{\rm{g}}^{2}+\\{\kern 40pt}\dfrac{1}{p{{r}^{3}}}\dfrac{\gamma z{{M}^{2}}Tp_{\rm{sc}}^{3}}{8{{\pi }^{3}}{{h}^{3}}{{\rm{R}}^{2}}T_{\rm{sc}}^{3}}q_{\rm{g}}^{3} $ | (8) |
式中:
R—摩尔气体常数,R=8.314 J/(mol·K)。
边界条件
| $ \left\{ \begin{matrix}p\left| _{r={{r}_{\rm{w}}}}={{p}_{\rm{wf}}} \right. \\p\left| _{r={{r}_{\rm{e}}}}={{p}_{\rm{e}}} \right. \\\end{matrix} \right. $ | (9) |
式中:
碳酸盐岩高温高压气井的三项式产能方程为
| $ p_{\rm{e}}^{2}-p_{\rm{wf}}^{2}=A{{q}_{\rm{g}}}+Bq_{\rm{g}}^{2}+Cq_{\rm{g}}^{3} $ | (10) |
式中:
式(10) 中,系数
| $ \left\{ \begin{array}{l} A=\dfrac{\mu zT{{p}_{\rm{sc}}}}{\pi Kh{{T}_{\rm{sc}}}}\ln \dfrac{r_{\rm{e}}}{{{r}_{\rm{w}}}} \\[6pt] B=\dfrac{\beta zMTp_{\rm{sc}}^{2}}{2{{\pi }^{2}}{{h}^{2}}{\rm R}T_{\rm{sc}}^{2}}\left( \dfrac{1}{{{r}_{\rm{w}}}}-\dfrac{1}{{{r}_{\rm{e}}}} \right) \\[6pt] C=\dfrac{\gamma z{{M}^{2}}Tp_{\rm{sc}}^{3}}{8{{\pi }^{3}}{{h}^{3}}{{\rm R}^{2}}T_{\rm{sc}}^{3}}\left( \dfrac{1}{r_{\rm{w}}^{2}}-\dfrac{1}{r_{\rm{e}}^{2}} \right) \\[6pt] \end{array} \right. $ | (11) |
从式(10) 可以看出,对于碳酸盐岩高温高压气井产能方程,存在3种流动阻力项。
4 约束优化算法研究区的碳酸盐岩储层属于缝洞型储层,生产压差很小,即使产量相差较大,生产压差差别也较小,产能曲线经常出现负斜率。
因此,采用最优化分析方法中的约束优化算法来解决这一问题,针对多个测试制度[15],根据式(10),有
| $ p_{\rm{e}}^2{\rm{ - }}\mathit{p}_{{\rm{wf}},i}^2 = \mathit{A}{q_{{\rm{g}},i}}{\rm{ - }}\mathit{Bq}_{{\rm{g}}i}^2{\rm{ + }}\mathit{Cq}_{{\rm{g}},i}^3{\rm{ ,}}(i = 1,2, \cdots ,n) $ | (12) |
式中:
为了实现计算井底压力值与实测值的最优拟合,需要构造非线性优化模型
| $ \left\{ \begin{array}{l} E\!=\!\min \sum\limits_{i=1}^{n}{\left( {{p}_{\rm{wf}i}}-\sqrt{p_{\rm{e}}^{2}\!-\!A{{q}_{\rm{g}}}\!-\!Bq_{\rm{g}}^{2}\!-\!Cq_{\rm{g}}^{3}} \right)} \\ p_{\rm{e}}^{2} > \max{{p}_{\text{wf}, i}} \\ A, B, C > 0 \\ \end{array} \right. $ | (13) |
上式如果去掉约束条件,其实就是一般的最小二乘问题,有的试井资料品质很好,用简单回归就能处理。但是对于碳酸盐岩气藏实际复杂情况,可能会使曲线发生弯曲,因此加约束的目的就是削弱复杂情况的影响,同时可保证产能方程的各系数均为正常值。
5 实例计算 5.1 常规方法塔X01井关井静压梯度为0.286 MPa/(×100 m),低于生产期间各工作制度下的流压梯度,表明关井后井筒中出现了气液分离现象,形成井底积液。因此不能按照实测的静压梯度折算至井底求取静压,可采用以下方法对静压、产能进行计算。
设实测静压
| $ p_{\rm{e}}'^{2}-p_{\rm{wf}}^{2}+{\rm{c}}=A{{q}_{\rm{g}}}+Bq_{\rm{g}}^{2} $ | (14) |
式中:
c—常数,MPa
式(14) 中,常数c物理意义就是真实静压平方与实测静压平方之差,因此,c是由地层静压测量不准造成的,求出c之后,就可以求出真实静压,从而进一步进行产能分析。
c可用如下的方法求解:按照二项式方法作出
求得c后作
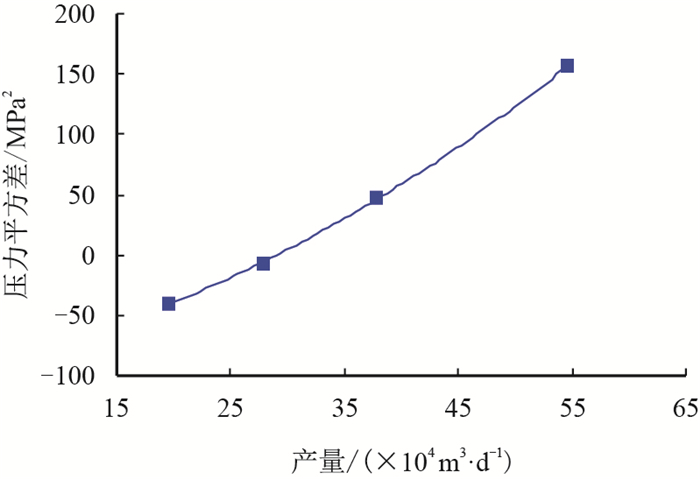
具体到该井,根据表 6的流压和产量,可以作出
 |
|
图2
|
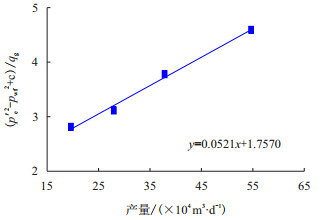
经
 |
|
图3
|
进一步求得无阻流量为330.00×104 m3/d。
5.2 新方法采用约束优化算法进行实例计算,可以快速实现产能方程的求解。考虑产能方程为二项式时,采用约束优化算法对数据进行解释得到的无阻流量为309.12×104 m3/d,与常规方法极为接近,误差均在7%以内。与常规方法相比,该方法不需要多次拟合调整以获取压力平方因子。
但是,以上解释结果都没有考虑到脉冲阻力造成的压力损失。对于碳酸盐岩高温高压气井,测试阶段的产量极高,不可忽略脉冲效应的对产能的影响。因此,利用约束优化算法,获得了塔X01井的三项式产能方程系数:
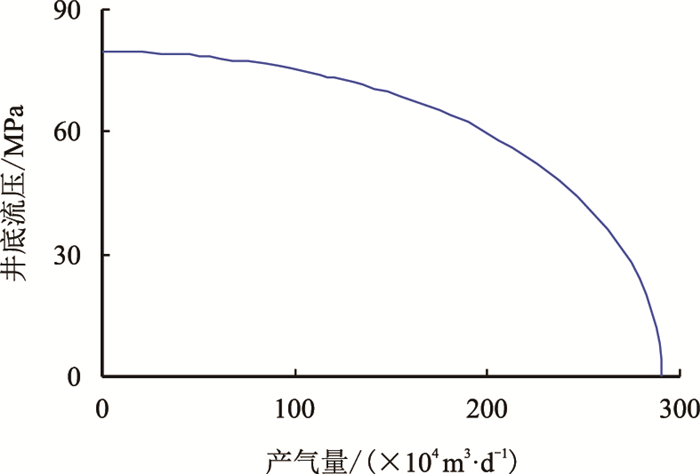 |
| 图4 约束优化方法计算结果 Fig. 4 The calculation results constrained optimization algorithm |
(1) 由于大量泥浆的漏失,测试时泥浆产出影响了资料质量。利用测试点压力对塔X01井进行产能分析,将会错误地判断气井的产能,从而影响气井生产制度的建立。
(2) 利用前人研究气体在垂直管道中的流动机理结果,优选出适合该井区高气液比的井筒两相流计算方法,根据大量实测数据,应用气液比对计算方法进行校正,提高了计算精度,为塔X01井的产能分析和试井解释提供正确的数据来源。
(3) 碳酸盐岩高温高压气井,测试阶段的产量极高,流动通道复杂多变,三项式产能方程更能描述该类气藏的特征。进一步利用约束优化算法,能够快速计算,并保障产能方程的各系数均为正值。
| [1] |
李军诗, 门成全, 王晓冬, 等. 克拉2气田克拉203井产能分析与试井解释[J].
新疆石油学院学报, 2004, 16(3): 20–23.
LI Junshi, MEN Chengquan, WANG Xiaodong, et al. Productivity analysis and well testinterpretation of well kela 203 in gas field[J]. Journal of Xinjiang Petroleum Institute, 2004, 16(3): 20–23. doi: 10.3969/j.issn.1673-2677.2004.03.006 |
| [2] |
黄孝海, 李晓平, 袁淋. 异常高压产水气井三项式方程推导及应用[J].
岩性油气藏, 2014, 26(5): 119–123.
HUANG Xiaohai, LI Xiaoping, YUAN Lin. Deducitong and application of trinpmial equation for water producing gas well with abnormal pressure[J]. Lithologic Reservoirs, 2014, 26(5): 119–123. doi: 10.3969/j.issn.1673-8926.2014.05.022 |
| [3] |
藤赛男, 梁景伟, 李元生, 等. 异常高压气藏常规产能方程评价方法研究[J].
油气井测试, 2011, 20(6): 15–19.
TENG Sainan, LIANG Jingwei, LI Yuansheng, et al. Abnormal high pressure gas reservoir appraisal method for conventional productivity equation[J]. Well Testing, 2011, 20(6): 15–19. doi: 10.3969/j.issn.1004-4388.2011.06.005 |
| [4] |
陈春艳. 异常高压气藏气井产能方程求解的简易方法[J].
天然气工业, 2007, 27(4): 88–89.
CHEN Chunyan. Abnormal high pressure gas well productivity equation of gas reservoir and simple method[J]. Natural Gas Industry, 2007, 27(4): 88–89. doi: 10.3321/j.issn:1000-0976.2007.04.028 |
| [5] |
罗银富, 黄炳光, 王怒涛, 等. 异常高压气藏气井三项式产能方程[J].
天然气工业, 2008, 28(12): 81–82.
LUO Yinfu, HUANG Bingguang, WANG Nutao, et al. Trinomial deliverability equation for a gas well in abnormally high pressure gas reservoirs[J]. Natural Gas Industry, 2008, 28(12): 81–82. doi: 10.3787/j.issn.1000-0976.2008.12.023 |
| [6] | HU Yong, ZHONG Fuxun. Wellbore fluid to study the influence of gas well test data[C]. SPE 22437, 1992. |
| [7] |
刘慰宁, 陈钦雷. 均质油藏考虑井筒相再分布的试井分析[J].
天然气工业, 1992, 12(1): 54–59.
LIU Weining, CHEN Qinlei. Homogeneous reservoir considering wellbore phase distribution of well test analysis[J]. Natural Gas Industry, 1992, 12(1): 54–59. |
| [8] | HEGEMAN P S, HALLFORD D L, JOSEPH J A. Well test analysis with changing wellbore storage[J]. SPE Formation Evaluation, 1993, 8(3): 201–207. doi: 10.2118/-21829-PA |
| [9] |
杨川东.
采气工程[M]. 北京: 石油工业出版社, 1997.
YANG Chuandong. Natural gas production engineering[M]. BeiJing: Petroleum Industry Press, 1997. |
| [10] |
王毅忠, 刘庆文. 计算气井最小携液临界流量的新方法[J].
大庆石油地质与开发, 2007, 26(6): 82–85.
WANG Yizhong, LIU Qingwen. A new method to calculate them inimum critical liquids carrying flow rate for gas wells[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26(6): 82–85. doi: 10.3969/j.issn.1000-3754.2007.06.021 |
| [11] |
彭朝阳. 气井携液临界流量研究[J].
新疆石油地质, 2010, 31(1): 72–74.
PENG Chaoyang. Study on critical liquid-carrying flow rate for gas well[J]. Xinjiang Petroleum Geology, 2010, 31(1): 72–74. |
| [12] |
陈元千. 气井垂直管流计算方法的推导与应用[J].
断块油气藏, 2010, 17(4): 443–447.
CHEN Yuanqian. Derivation and application of calculating methods of vertical pipe fiow in gas wells[J]. Fault Block Oil-Gas Reservoir, 2010, 17(4): 443–447. |
| [13] |
童敏, 齐明明, 马培新, 等. 高气液比气井井底流压计算方法研究[J].
石油钻采工艺, 2006, 28(4): 71–73.
TONG Min, QI Mingming, MA Peixin, et al. Study on computingm ethod of bottom-hole flow pressure of gas well with high gas-liquid ratio[J]. Oil Drilling & Production Technology, 2006, 28(4): 71–73. |
| [14] | FIROOZABADI A, KATZ D L. An analysis of highvelocity gas flow through porous media[J]. JPT, 1979, 31(2): 211–216. doi: 10.2118/6827-PA |
| [15] | TURNER R G, HUBBARD M G, DUKLER A E. Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells[J]. JPT, 1969, 21(11): 75–82. |
 2017, Vol. 39
2017, Vol. 39


