2. 北京华油海川能源技术开发有限公司, 北京 海淀 100081
2. Beijing Huayou Haichuan Energy Technology Development Co. Ltd., Haidian, Beijing 100081, China
准确及时地获得井下信息是实现快速优质钻井的重要保障,随钻测量技术的发展极大地提高了钻井效率。气体钻井以提高钻井速度、发现和保护储层、减少或避免井漏等优势在石油开采过程中应用比较广泛[1-2],但是由于气体钻井没有液相钻井液的循环,常规的泥浆脉冲遥测技术无法使用,电磁波信号在低电阻率地层中衰减严重,传输距离有限[3]。
国外关于声波遥测技术的研究起步较早,早在1948年美国太阳石油公司就开展了利用声波传输井下测量数据的研究[4];1988年美国新墨西哥州Sandia国家实验室的Drumheller开展对钻柱中的声波传播特性和衰减规律的理论研究,为该项技术的发展奠定了理论基础[5];哈里伯顿公司研发了非随钻应用的声波遥测系统(Acoustic Telemetry System)[6-7];2007—2011年,XACT公司先后公布了其开发的声波遥测样机的现场试验数据,声波信号的最大传输距离为2 500 m[8-9]。国内在声波遥测技术上存在不小的差距,目前还处于理论研究阶段。中国石油大学(华东)管志川团队引领了相关领域的研究工作,李志刚等分析了随钻声波遥测中的关键问题[10],赵国山等研究了声波在钻柱中的传播特性[11],马西庚等通过模拟实验对声波传播过程中的影响因素进行了分析[12],管志川等针对钻柱的结构特性对声波的传输的影响作用开展了研究[13-14]。
上述研究成果都是针对声波信号在钻柱本体钢结构中的传播,但由于钻井工况的复杂致使信号传输过程中易受到钻头破岩、井壁摩擦碰撞等干扰因素的影响,声波信号的有效传输距离比较有限。本文参照医用听诊器的工作原理,提出在气体钻井过程中以钻柱内气体为信道进行井下声波信号传输的方法,通过建立钻柱内声波传播的数学模型分析声波传播的衰减规律,并运用声波导理论分析钻柱的声波导特性,同时利用实验验证了理论分析的可靠性,为建立气体钻井钻柱内声波遥测通道提供依据。
1 气体钻井钻柱内声波传播衰减规律 1.1 基本假设建立气体钻井钻柱内声波传播的数学模型,基于几点假设:(1) 考虑钻柱内一维气体流动;(2) 钻柱内声波是微扰动压力波;(3) 声波传播是非可逆绝热过程;(4) 忽略气体的自身重力;(5) 不考虑声波传播过程中的波形畸变和非线性效应。
1.2 基本方程钻柱内气体介质流动的连续性方程
| $ \dfrac{{\partial {\rho _{\text{g}}}}}{{\partial t}} + {\rho _{\text{g}}}\dfrac{{\partial {u_{\text{g}}}}}{{\partial x}} + {u_{\text{g}}}\dfrac{{\partial {\rho _{\text{g}}}}}{{\partial x}} = 0 $ | (1) |
钻柱内气体介质流动的动量方程
| $ {\rho _{\rm{g}}}\dfrac{{\partial {u_{\rm{g}}}}}{{\partial t}} + {\rho _{\rm{g}}}{u_{\rm{g}}}\dfrac{{\partial {u_{\rm{g}}}}}{{\partial x}} = - \dfrac{{\partial {p_{\rm{g}}}}}{{\partial x}} - \\[5pt]{\kern 40pt}\dfrac{{{f_{\rm{g}}}}}{{2d}}u_{\rm{g}}^2 - \dfrac{2}{d}\sqrt {2{\mu _{\rm{g}}}{\rho _{\rm{g}}}{\rm{\omega }}} {u_{\rm{g}}} $ | (2) |
气体介质状态方程
| $ \dfrac{{\partial {p_{\rm{g}}}}}{{\partial t}} + {u_{\rm{g}}}\dfrac{{\partial {p_{\rm{g}}}}}{{\partial x}} = \gamma \dfrac{{{p_{\rm{g}}}}}{{{\rho _{\rm{g}}}}}\left( {\dfrac{{\partial {\rho _{\rm{g}}}}}{{\partial t}} + {u_{\rm{g}}}\dfrac{{\partial {\rho _{\rm{g}}}}}{{\partial x}}} \right) $ | (3) |
利用线性化小扰动理论对气体流动的控制方程式(1)~式(3) 进行处理,得到声波传播的控制方程。声波传播引起的气体流场基本态
| $ {p_{\rm{g}}} = {p_{{\rm{g}}0}} + {p'_{\rm{g}}} $ | (4) |
| $ {\rho _{\rm{g}}} = {\rho _{{\rm{g}}0}} + {\rho '_{\rm{g}}} $ | (5) |
| $ {u_{\rm{g}}} = {u_{{\rm{g}}0}} + {u'_{\rm{g}}} $ | (6) |
| $ \dfrac{p_{\rm{g}}'}{p_{{\rm{g}}0}}\sim \dfrac{\rho_{\rm{g}}'}{\rho_{{\rm{g}}0}} \sim \dfrac{u_{\rm{g}}'}{u_{{\rm{g}}0}} \sim \delta $ | (7) |
将式(4)~式(6) 分别代入气体流动控制方程式(1)~式(3) 得到声波传播的控制方程
| $ \dfrac{{\partial {{\rho}_{\rm{g}}}'}}{{\partial t}} + {\rho _{{\rm{g}}0}}\dfrac{{\partial {{u}_{\rm{g}}'}}}{{\partial x}} + {u_{{\rm{g}}0}}\dfrac{{\partial {{\rho}_{\rm{g}}'}}}{{\partial x}} = 0 $ | (8) |
| $ {\rho _{{\rm{g}}0}}\dfrac{{\partial {{u}_{\rm{g}}'}}}{{\partial t}} + {\rho _{{\rm{g}}0}}{u_{{\rm{g}}0}}\dfrac{{\partial {{u}_{\rm{g}}'}}}{{\partial x}} = - \dfrac{{\partial {{p}_{\rm{g}}'}}}{{\partial x}} - \\[5pt]{\kern40pt}\dfrac{{{f_{\rm{g}}}}}{d}{u_{{\rm{g}}0}}{u'_{\rm{g}}} - \dfrac{2}{d}\sqrt {2{\mu _{\rm{g}}}{\rho _{{\rm{g}}0}}{\rm{\omega }}} u_{\rm g}' $ | (9) |
| $ \dfrac{{\partial {{p}_{\rm{g}}'}}}{{\partial t}} + {u_{{\rm{g}}0}}\dfrac{{\partial {{p}_{\rm{g}}'}}}{{\partial x}} = \gamma \dfrac{{{p_{{\rm{g}}0}}}}{{{\rho _{{\rm{g}}0}}}}\left( {\dfrac{{\partial {{\rho '}_{\rm{g}}}}}{{\partial t}} + {u_{{\rm{g}}0}}\dfrac{{\partial {{\rho '}_{\rm{g}}}}}{{\partial x}}} \right) $ | (10) |
柱内由声波传播引起的扰动的控制变量可表示为
| $ \left[{\begin{array}{*{20}{c}} {{{p}_{\rm{g}}'}}\\ {{{\rho}_{\rm{g}}'}}\\ {{{u}_{\rm{g}}'}} \end{array}} \right] = {\rm{\delta }}\left[{\begin{array}{*{20}{c}} {{p_{{\rm{g0}}}}}\\ {{\rho _{{\rm{g0}}}}}\\ {{u_{{\rm{g0}}}}} \end{array}} \right]{{\rm{e}}^{{\rm{i}}\left( {{\rm{\omega }}t - kx} \right)}} $ | (11) |
将式(11) 代入声波传播控制方程,忽略二阶小量,可得到
| $ \left( {{\rm{\omega }} - {u_{{\rm{g}}0}}k} \right){\rho '_{\rm{g}}} - {\rho _{{\rm{g}}0}}k{u'_{\rm{g}}} = 0 $ | (12) |
| $ \left[{{\rm{i}}\left( {\dfrac{{{f_{\rm{g}}}{u_{{\rm{g}}0}}}}{{{\rho _{{\rm{g}}0}}d}} + \dfrac{2}{{d{\rho _{{\rm{g}}0}}}}\sqrt {2{\mu _{\rm{g}}}{\rho _{{\rm{g}}0}}{\rm{\omega }}} } \right)-{\rm{\omega }}} \right]{u'_{\rm{g}}} +\\{\kern 40pt} \dfrac{k}{{{\rho _{{\rm{g}}0}}}}{p'_{\rm{g}}} = 0 $ | (13) |
| $ {\rho _{{\rm{g}}0}}{p'_{\rm{g}}} - \gamma {p_{{\rm{g}}0}}{\rho '_{\rm{g}}} = 0 $ | (14) |
式(12)~式(14) 是关于扰动控制变量
| $ \left[{\begin{array}{*{20}{c}} {\rm{\omega }}&{-{\rho _{{\rm{g}}0}}k}&0\\ 0&{{\rm{i}}\left( {\dfrac{{{f_{\rm{g}}}{u_{{\rm{g}}0}}}}{{{\rho _{{\rm{g0}}}}d}} \!+\! \dfrac{2}{{d{\rho _{{\rm{g}}0}}}}\sqrt {2{\mu _{\rm{g}}}{\rho _{{\rm{g}}0}}{\rm{\omega }}} } \right) \!-\! {\rm{\omega }}}&{\dfrac{k}{{{\rho _{{\rm{g}}0}}}}}\\ {-\gamma {p_{{\rm{g}}0}}}&0&{{\rho _{{\rm{g}}0}}} \end{array}} \right]{\rm{ = }}0 $ | (15) |
求解色散方程,可以得到关于波数k的隐式表达式
| $ \dfrac{1}{{\gamma {p_{{\rm{g}}0}}}}\left[{-{\rho _{{\rm{g}}0}}{\rm{\omega }} + {\rm{i}}\left( {\dfrac{{{f_{\rm{g}}}{u_{{\rm{g}}0}}{\rm{\omega }}}}{{{\rho _{{\rm{g}}0}}d}} + \dfrac{{2{\rm{\omega }}}}{d}\sqrt {2{\mu _{\rm{g}}}{\rho _{{\rm{g}}0}}{\rm{\omega }}} } \right)} \right] +\\[5pt]{\kern 40pt}{k^2} = 0 $ | (16) |
式(16) 是一个关于波数k的复数系一元二次方程,通过求解可得到两个复数系根。一个根的实部为正数,表示声波沿正方向传播;另一个根的实部为负数,表示声波负方向传播。根据这两个根,可以求得声波的传播速度c和衰减系数η[15]
| $ c = {\left\{ {{{\rm{\omega }}^2} + {{\left[{{{\rm{\omega }}^4} + {{\left( {\dfrac{{{f_{\rm{g}}}{u_0}{\rm{\omega }}}}{{{\rho _{{\rm{g}}0}}d}} + \dfrac{{2{\rm{\omega }}}}{d}\sqrt {\dfrac{{2{\mu _{\rm{g}}}{\rm{\omega }}}}{{{\rho _{{\rm{g}}0}}}}} } \right)}^2}} \right]}^{\frac{1}{2}}}} \right\}^{ - \frac{1}{2}}}\cdot\\[5pt]{\kern 40pt}\dfrac{{\rm{\omega }}}{{\sqrt {\dfrac{{{\rho _{{\rm{g}}0}}}}{{2\gamma {p_{{\rm{g}}0}}}}} }} $ | (17) |
| $ \eta = {\left\{ {{{\left[{{{\left( {\dfrac{{{f_{\rm{g}}}{u_0}{\rm{\omega }}}}{{{\rho _{{\rm{g}}0}}d}} + \dfrac{{2{\rm{\omega }}}}{d}\sqrt {\dfrac{{2{\mu _{\rm{g}}}{\rm{\omega }}}}{{{\rho _{{\rm{g}}0}}}}} } \right)}^2} + {{\rm{\omega }}^4}} \right]}^{\frac{1}{2}}} - {{\rm{\omega }}^2}} \right\}^{\frac{1}{2}}} \cdot \\[5pt]{\kern 40pt}\sqrt {\dfrac{{{\rho _{{\rm{g}}0}}}}{{2\gamma {p_{{\rm{g}}0}}}}} $ | (18) |
模型的计算结果将在后文的实验部分结合具体实例与实测数据进行对比。
2 气体钻井钻柱声波导特性分析气体钻井过程中所使用的钻柱是由多根钻杆连接而成,整体结构类似于一根长直圆管道,在声学领域可视作圆柱型波导管来处理。同时钻杆的接箍处会有内截面积的变化,由于声波的反射作用会造成一定程度的衰减。
2.1 钻柱内声波传输截止频率声波在无界自由空间中传播时波阵面会呈球面状发散,而将声波限制于受管壁束缚的管道中传播时,管子的形状、尺寸以及管壁材料都会对声波的传播产生影响,在一定条件下会以相对简单的平面波形式进行传播。
在柱坐标下求解声波方程(19),假设钻柱内壁是刚性的,内部气体为理想流体。
| $ \dfrac{1}{r}\dfrac{\partial }{{\partial r}}\left( {r\dfrac{{\partial p}}{{\partial r}}} \right) + \dfrac{1}{{{r^2}}}\dfrac{{{\partial ^2}p}}{{\partial {\theta ^2}}} + \dfrac{{{\partial ^2}p}}{{\partial {z^2}}} = \dfrac{1}{{{c^2}}}\dfrac{{{\partial ^2}p}}{{\partial {t^2}}} $ | (19) |
利用分离变量法进行求解,将解
| $ \left\{ \begin{array}{l} \dfrac{{{{\rm{d}}^2}Z}}{{{\rm{d}}{z^2}}} + {k_z}^2Z = 0\\[5pt] \dfrac{{{{\rm{d}}^2}\varTheta }}{{{\rm{d}}{\theta ^2}}} + {m^2}\varTheta = 0\\[5pt] \dfrac{{{{\rm{d}}^2}R}}{{{\rm{d}}{r^2}}} + \dfrac{1}{r}\dfrac{{{\rm{d}}R}}{{{\rm{d}}r}} + \left( {{k_r}^2 - \dfrac{{{m^2}}}{{{r^2}}}} \right)R = 0 \end{array} \right. $ | (20) |
式(20) 中
| $ {k^2} = \dfrac{\omega }{c} = {k_z}^2 + {k_r}^2 $ | (21) |
因为
| $ Z\left( z \right) = {A_z}{{\rm e}^{ - {\rm i}{k_z}z}} $ | (22) |
关于
| $ \varTheta \left( \theta \right) = {A_\theta }\cos \left( {m\theta + {\varphi _m}} \right) $ | (23) |
关于
| $ \dfrac{{{{\rm{d}}^2}R}}{{{\rm{d}}{x^2}}} + \dfrac{1}{x}\dfrac{{{\rm{d}}R}}{{{\rm{d}}x}} + \left( {1 - \dfrac{{{m^2}}}{{{x^2}}}} \right)R = 0 $ | (24) |
其一般解可表示为
| $ R\left( {{k_r}r} \right) = {A_r}{J_m}\left( {{k_r}r} \right) + {B_r}{N_m}\left( {{k_r}r} \right) $ | (25) |
| $ {p_m} = {A_m}{J_m}\left( {{k_r}r} \right)\cos \left( {m\theta - {\varphi _m}} \right){{\rm{e}}^{{\rm{i}}\left( {\omega t - {k_z}z} \right)}} $ | (26) |
对应的径向速度为
| $ {v_{rm}} = \dfrac{{\rm{i}}}{{{\rho _{\rm g}}\omega }}\dfrac{{\partial {p_m}}}{{\partial r}} = {A_m}\dfrac{{{\rm{i}}{k_r}}}{{{\rho _{\rm g}}\omega }}\left[{\dfrac{{{\rm d}{J_m}\left( {{k_r}r} \right)}}{{{\rm d}\left( {{k_r}r} \right)}}} \right]\cdot\\[5pt]{\kern 40pt}\cos \left( {m\theta - {\varphi _m}} \right){{\rm{e}}^{{\rm{i}}\left( {\omega t - {k_z}z} \right)}} $ | (27) |
由于假设内壁面是刚性的,在壁面
| $ {J_{m - 1}}\left( {{k_r}a} \right) = {J_{m + 1}}\left( {{k_r}a} \right), {\kern 10pt} (m>0) $ | (28) |
| $ {J_1}\left( {{k_r}a} \right) = 0, {\kern 10pt} (m=0) $ | (29) |
求解方程可以得到一系列根值,用阶数区分表示这些根值,有
| $ {p_{mn}} = {A_{mn}}\cos \left( {m\theta - {\varphi _m}} \right){J_m}\left( {{k_{mn}}r} \right){{\rm{e}}^{{\rm{i}}\left( {\omega t - {k_z}z} \right)}} $ | (30) |
式(30) 代表钻柱内的第(
式(30) 中任一组(
| $ p = \sum\limits_{mn} {p_{mn}} = \sum\limits_m^\infty \sum\limits_n^\infty {A_{mn}}\cos (m\theta - {\phi _m}){J_m}({K_{mn}}r)\cdot\\[5pt]{\kern 40pt}{{\rm e}^{{\rm{j}}(\omega t - {k_z}z)}} $ | (31) |
高次波实质上就是与钻柱轴线成一定夹角经壁面不断反射而行进的平面波,当夹角为90°时,这束波就不能向轴线方向前进,会在钻柱横截面上形成驻波。
如图 1所示,高次波由波阵面
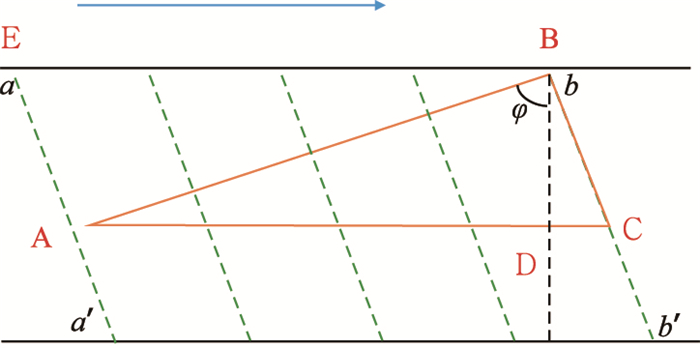 |
| 图1 高次波传播速度分析 Fig. 1 Velocity analyses of high order wave propagation |
当声波传至钻杆接箍处由于内截面积的变化会发生反射现象,致使只有一部分声波可以透过钻柱变径处继续向前传播,如图 2所示,这也是声波在钻柱内传播过程中引起衰减的另一方面原因。
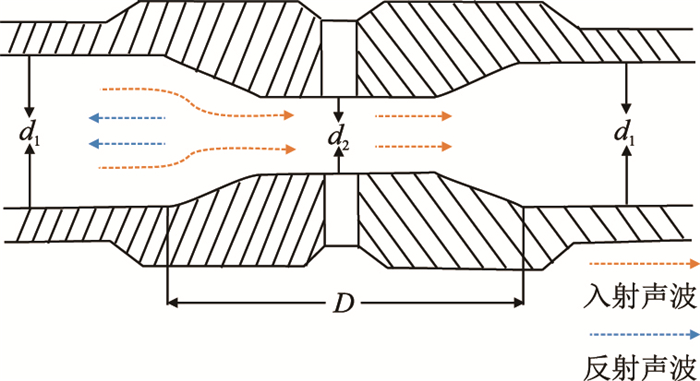 |
| 图2 钻柱接箍处声波反射 Fig. 2 Acoustic wave reflection of drill pipe collar |
钻杆本体的内截面积为
| $ {t_{\rm{p}}} = \frac{2}{{{{\left[{4{{\cos }^2}kD + {{\left( {{S_{12}} + {S_{21}}} \right)}^2}{{\sin }^2}kD} \right]}^{1/2}}}} $ | (32) |
式(32) 中,
在钻柱内声波传播衰减规律和钻柱声波导特性理论分析的基础上,通过管道声波信号传输实验验证理论分析的准确性,采用对相同声源激励下不同传播距离所接收到的声波信号同步分析的方法,实验系统设计如图 3所示。
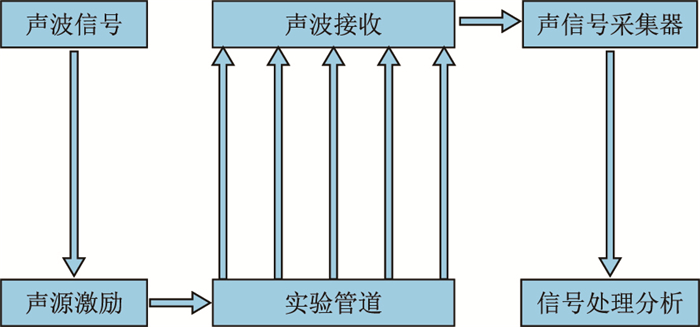 |
| 图3 实验系统设计 Fig. 3 Design of experiment system |
(1) 实验管道:选用与气体钻井常用钻具尺寸相近的实验管道,内径分别为106,86,73 mm,总长42 m。声波信号采集位置至声源距离分别为1,11,21,31,41 m。
(2) 声源:采用声波信号生成软件提供所需信号,能够输出设定频率和幅值的声波信号,又能以线性或对数扫频的方式在设定的频率及时间范围内产生指定波形的信号。采用15寸同轴扬声器作为声源激励,频率响应37~18 000 Hz,最大功率500 W。
(3) 声波信号采集:在实验管道不同位置处装入微型驻极体电容式传声器来接收声波信号,频率响应20~20 000 Hz,使用多通道外置声卡实现声波信号的同步采集。
(4) 声波信号处理:运用声信号分析软件在信号幅值和频谱两方面对多通道声卡所采集到的声波信号进行处理分析。图 4是实验系统所用设备,其中a、b、c、d分别为实验管道、扬声器、声信号传感器和多通道声信号采集卡与驱动扬声器的功放机。
 |
| 图4 实验设备 Fig. 4 Equipments of experiment system |
声学领域普遍使用对数标度来度量声压,称为声压级,其单位常用dB,以符号
| $ S_{\rm PL} = 20\lg \dfrac{{{p_{\rm{e}}}}}{{{p_{{\rm{ref}}}}}} $ | (33) |
在空气中,参考声压一般取为2×10-5 Pa,这个数值是正常人耳对1 kHz声音刚能察觉其存在的声压值[17]。实验采用100,500,1 000 Hz三档固定频率的正弦声波信号作为输出,在实验管道上每个采集点采集声波信号的幅值,图 5、图 6、图 7分别为3种内径尺寸实验管道中实测声波信号幅值与理论模型计算结果的对比。
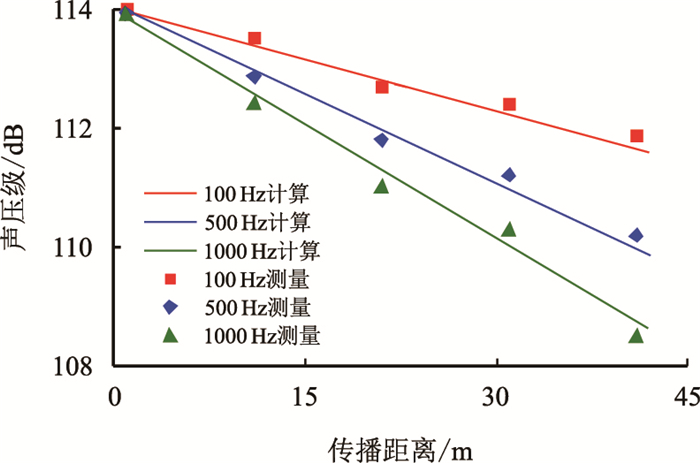 |
| 图5 实测声波信号幅值与计算结果对比(106 mm管道) Fig. 5 Comparison between measured acoustic signal amplitudes and the calculations (106 mm pipe) |
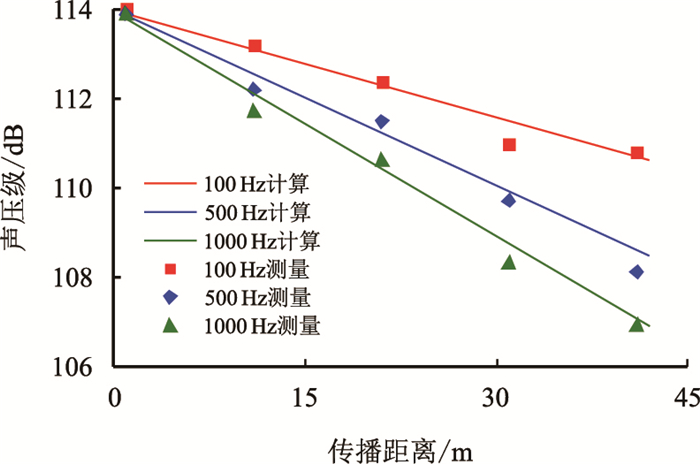 |
| 图6 实测声波信号幅值与计算结果对比(86 mm管道) Fig. 6 Comparison between measured acoustic signal amplitudes and the calculations(86 mm pipe) |
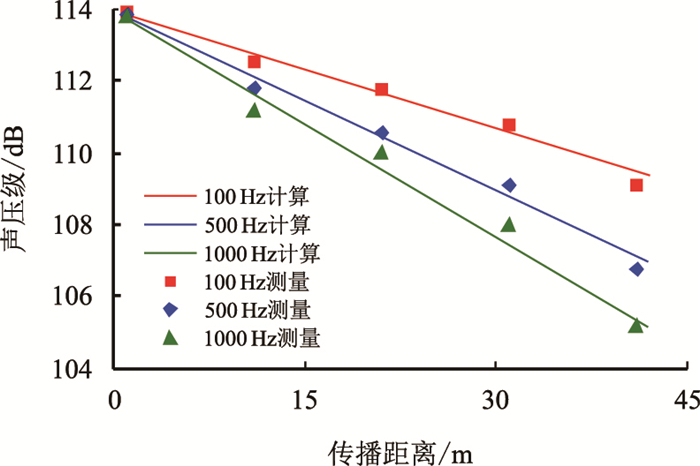 |
| 图7 实测声波信号幅值与计算结果对比(73 mm管道) Fig. 7 Comparison between measured acoustic signal amplitudes and the calculations(73 mm pipe) |
图 5中横坐标代表声波信号在实验管道内的传输距离,纵坐标代表声波信号的幅值。可以看出在内径106 mm实验管道中随着声波信号传播距离的增加,声波信号的幅值呈递减趋势,同时声波信号的频率越高在传播过程中衰减程度越大。在采集点所测得的信号幅值与理论计算差值基本都在0.5 dB内,且具有相同的变化规律,说明模型的计算具备足够的精度。
由图 6和图 7可以观察出与图 5相同的规律,随着声波频率的提升,声波信号在实验管道传输过程中衰减程度会逐渐加剧,实测结果与理论计算的吻合度较高。同时可以发现实验管道的内径尺寸越小,相同位置所接收到的声波信号幅值越低。因此可以得出这样的结论,钻柱内声波信号传输过程中的衰减随声波频率的提高而加剧,钻柱内径尺寸越小,声波信号衰减越严重。
3.2.2 管内声波截止频率根据钻柱声波导特性的理论分析进行计算,得出不同尺寸实验管道内各阶声波的简正频率,如表 1所示。
| 表1 实验管道内各阶声波计算简正频率 Table 1 Calculated normal frequencies of each order acoustic wave in experimental pipes |
实验测试使用50~20 000 Hz时长10 s的扫频正弦声波信号作为输出,分别在实验管道上每个采集点记录声波信号的频谱曲线,图 8、图 9、图 10分别为内径106,86,73 mm实验管道所采集到的声波信号频谱曲线。频谱分析是信号分析领域常用的方法,是将时域声波信号通过傅里叶变换转换成与频率有关的函数,从频谱曲线上可以直观地看出每个频段声波信号在不同传输距离的幅值。
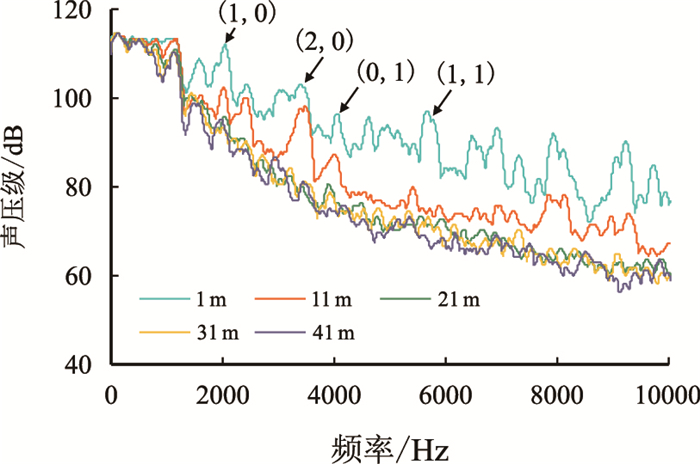 |
| 图8 内径106 mm管道声波频谱 Fig. 8 Acoustic wave spectrum in the pipe with 106 mm internal diameter |
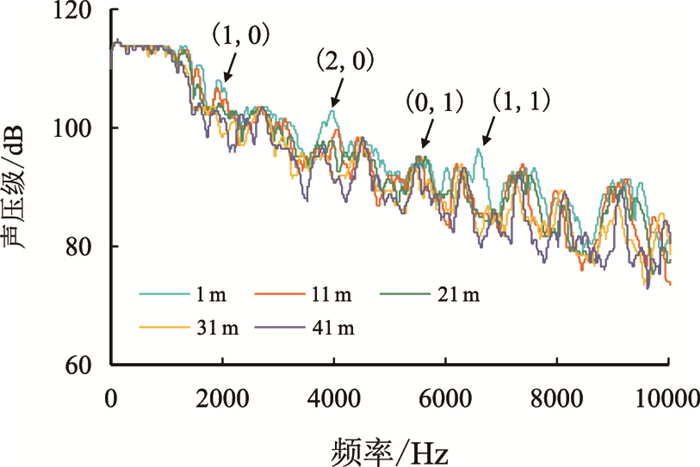 |
| 图9 内径86 mm管道声波频谱 Fig. 9 Acoustic wave spectrum in the pipe with 86 mm internal diameter |
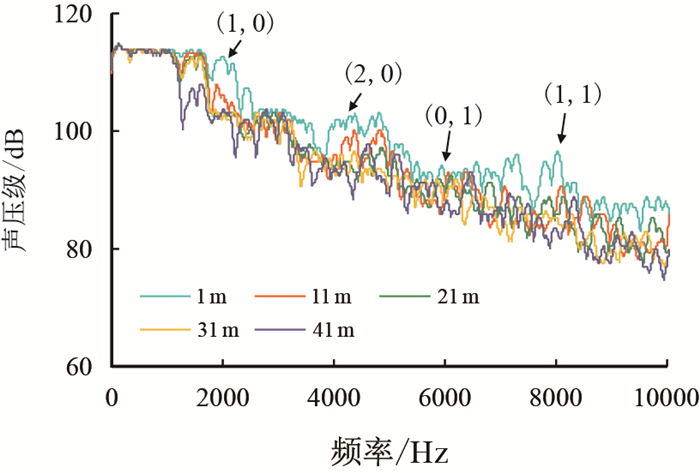 |
| 图10 内径73 mm管道声波频谱 Fig. 10 Acoustic wave spectrum in the pipe with 73 mm internal diameter |
图 8中每条曲线代表在内径106 mm实验管道的不同位置所接收到的声波信号绘制出的频谱曲线,横轴为声波信号频率,纵轴代表对应频率声信号的幅值,曲线之间的距离反映对应频率声信号的衰减情况。可以看出几条曲线起始端基本重合,随着频率的升高曲线之间的距离逐渐增大,说明随频率升高,声波信号衰减逐渐加重;同时在标注位置处曲线之间距离出现陡增,说明在对应频段声波信号幅值有明显降低,其对应位置与表 1中各次声波计算简正频率基本一致。这是因为在声波频率达到某次波的简正频率时,在管道中产生了相应的高次波,同时由于高次波的衰减要强于主波,致使该频段声波发生了明显的衰减。
由图 9可以看出,内径86 mm管道中声波信号的频谱曲线呈现了同样的规律,随着声波频率的提高传播过程中的衰减程度越严重,曲线间距陡增处所对应的声信号频率也与表 1中86 mm管道计算简正频率基本对应。所不同的是高频段的声信号幅值要明显高于106 mm管道,且曲线之间的距离也在缩小。
图 10中内径73 mm管道声信号幅值随频率变化的规律与另两根管道一致,标注处曲线间距的陡增也与表 1中计算数据相吻合。由以上三组实验数据还可以看出,管道内径尺寸越小,管道内各阶声波的简正频率越高,也就是说小尺寸的管道能够允许更高频率的声波信号在其中进行传输。
实验结果与计算截止频率的一致性验证了此前对钻柱声波声波导特性的理论分析。为此在设计气体钻井钻柱内声波信号传输的载波频率时,不仅要考虑声波信号衰减随频率的变化规律,还应当充分考虑不同尺寸钻具波导特性对声波信号的影响作用。
4 结论(1) 气体钻井钻柱内声波信号传输过程中的衰减程度与信号频率有关,声波信号频率越高传输过程中的衰减越严重。实验结果显示1 000 Hz声波信号幅值在40 m传输距离内比100 Hz声波信号多衰减60%。
(2) 钻柱的内径尺寸决定了内部各阶声波的截止频率,内径越大,声波的截止频率越低,允许通过的声波频率越低,实验中106 mm管道声波截止频率比73 mm管道低440 Hz。
(3) 在气体钻井钻柱内声波信号传输载波频率的选择上,应同时兼顾频率对声波信号衰减的影响作用和不同尺寸钻具的声波导特性,尽量选择钻柱截止频率内较低的频段,减少因高次波激发造成的衰减,延长声波信号的传输距离。
符号说明
i—虚数的虚部,无因次;
k—声波的波数,物理上定义为2
c—声波的传播速度,m/s;
η—声波传播衰减系数,无因次;
| [1] |
李皋, 孟英峰, 蒋俊, 等. 气体钻井的适应性评价技术[J].
天然气工业, 2009, 29(3): 53–71.
LI Gao, MENG Yingfeng, JIANG Jun, et al. Evaluation techniques on the adaptability of gas drilling[J]. Natural Gas Industry, 2009, 29(3): 53–71. doi: 10.3787/j.issn.-1000-0976.2009.03.016 |
| [2] |
张林伟. 气体钻井井下燃爆分析[J].
西南石油大学学报(自然科学版), 2012, 34(5): 146–152.
ZHANG Linwei. Analysis of Downhole Explosion in Gas Drilling[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(5): 146–152. doi: 10.3863/j.issn.1674-5086.2012.05.022 |
| [3] |
李林. 电磁随钻测量技术现状及关键技术分析[J].
石油机械, 2004, 32(5): 53–55.
LI Lin. Present situation and the key technical analysis of EMWD technology[J]. China Petroleum Machinery, 2004, 32(5): 53–55. doi: 10.3969/j.issn.1001-4578.2004.05.019 |
| [4] | DRUMHELLER D S. Acoustical properties of drill strings[J]. Journal of the Acoustical Society of America, 1989, 85(3): 1048–1064. doi: 10.1121/1.397488 |
| [5] | DRUMHELLER D S. Attenuation of sound waves in drill strings[J]. Journal of the Acoustical Society of America, 1993, 94(4): 2387–2396. doi: 10.1121/1.407458 |
| [6] | VIMAL S, WALLACE G, DON H J, SINAN S. Design considerations for a new high data rate LWD acoustic telemetry system[C]. SPE 88636, 2004. doi:10.2118/-88636-MS |
| [7] | GAO L, GARDNER W R, ROBBINS C, et al. Limits on data communication along the drillstring using acoustic waves[C]. SPE 95490, 2005. doi:10.2118/95490-PA |
| [8] | NEFF J M, CAMWELL P L. Field-test results of an acoustic MWD system[C]. SPE/IADC 105021, 2007. doi:10.-2523/105021-MS |
| [9] | REEVES M E, CAMWELL P L, MCRORY J. High speed acoustic telemetry network enables real-time along string measurements, greatly reducing drilling risk[C]. SPE 145566, 2011. doi:10.2118/145566-MS |
| [10] |
李志刚, 管志川, 王以法. 随钻声波遥测及其关键问题分析[J].
石油矿场机械, 2008, 37(9): 6–9.
LI Zhigang, GUAN Zhichuan, WANG Yifa. Acoustic telemetry while drilling and analysis on its key problems[J]. Oil Field Equipment, 2008, 37(9): 6–9. doi: 10.-3969/j.issn.1001-3482.2008.09.002 |
| [11] |
赵国山, 管志川, 刘永旺. 声波在钻柱中的传播特性[J].
中国石油大学学报(自然科学版), 2010, 34(1): 55–59.
ZHAO Guoshan, GUAN Zhichuan, LIU Yongwang. Acoustic transmission properties in drill string[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(1): 55–59. |
| [12] |
马西庚, 李超, 柳颖. 钻杆中声波传输特性测试[J].
中国石油大学学报(自然科学版), 2010, 34(4): 70–74.
MA Xigeng, LI Chao, LIU Ying. Transmission characteristics test of acoustic wave in drill string[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(4): 70–74. doi: 10.3969/j.issn.1673-5005.2010.-04.013 |
| [13] |
管志川, 刘永旺, 赵国山, 等. 钻柱结构对声波传输特性的影响[J].
石油学报, 2012, 33(4): 687–691.
GUAN Zhichuan, LIU Yongwang, ZHAO Guoshan, et al. An influence of the drill-string structure diversity on acoustic transmission characteristic[J]. Acta Petrolei Sinica, 2012, 33(4): 687–691. doi: 10.7623/syxb201204022 |
| [14] |
赵国山, 管志川, 都振川, 等. 井下钻柱信道的声传播特性[J].
石油学报, 2013, 34(1): 151–156.
ZHAO Guoshan, GUAN Zhichuan, DU Zhenchuan, et al. Acoustic propagation characteristics of the communication channel of downhole drill-string[J]. Acta Petrolei Sinica, 2013, 34(1): 151–156. doi: 10.7623/-syxb201301019 |
| [15] |
李红涛, 李皋, 孟英峰, 等. 充气钻井随钻测量脉冲信号衰减规律[J].
石油勘探与开发, 2012, 39(2): 233–237.
LI Hongtao, LI Gao, MENG Yingfeng, et al. Attenuation law of MWD pulses in aerated drilling[J]. Petroleum Exploration and Development, 2012, 39(2): 233–237. |
| [16] | 杜功焕, 宋哲民, 龚秀芳, 等. 声学基础[M]. 南京: 南京大学出版社, 2001: 238-302. |
| [17] | 吴胜举, 张明铎. 声学测量原理与方法[M]. 北京: 科学出版社, 2014: 101-119. |
 2017, Vol. 39
2017, Vol. 39


