钻井工程是一个工种、工序较多、多专业交叉、作业过程具有较强连续性的系统化工程,也是具有较强隐蔽性的地下工程之一[1-2]。在作业过程中,因为容易受到自然环境、管理水平、工艺技术水平和作业设备等因素的影响,不可避免地隐藏着多种潜在的隐患因素,如果施工人员对这些隐患因素不重视,极易导致作业过程中事故的发生[3]。一旦事故发生,就会对作业设备、周围环境造成一定程度的破坏,甚至威胁作业人员的人身安全,进而影响钻井作业的进度,影响国家的经济、社会效益。如何根据作业过程中的真实情况提前对隐患因素所造成的危害进行预测,给施工人员提供决策支持,将钻井过程中的风险降到最低,这是当前各大钻井公司关注的重点问题[4]。
目前,在钻井作业过程中,比较常用的安全评价方法有:层次分析法、模糊综合评价法以及灰色综合评价法等[5]。但是,层次分析法在获取评价因素阶段带有较强的主观性,很难保证计算结果的准确性[6];模糊综合评价法需要设定隶属度函数,操作难度较大;灰色综合评价法计算比较简单,但是当评语等级数量较多时,运算量较大[7]。粗糙集理论是一种刻画数据不充分性与模糊性的数学工具,它不需要除了问题描述所需要的数据集外的任何先验知识,就能确保在原问题决策能力不变的前提下,剔除数据集中的冗余数据和噪声数据[8]。BP神经网络是以误差反向传播算法为基础进行训练的多层前馈网络,具有自组织性、自学习能力、良好的容错能力以及很强的非线性映射能力等特点。本文把粗糙集和BP网络融合起来建立了一个钻井安全评价模型,首先通过粗糙集约简掉数据集中的冗余数据,简化BP网络的输入结构,然后根据约简结果构建的训练样本和测试样本对建立的网络模型进行训练和测试,保证安全评估模型的可靠性。
1 相关理论基础 1.1 粗糙集理论粗糙集(Rough Sets)理论是由波兰数学家Pawlak于1982年最先提出的,它对不完备和不确定信息有良好的分析能力,粗糙集不仅可以对知识约简,也可以发掘其中的规律[9-10]。
(1) 决策表:决策表是一个数据集合,它是粗糙集的研究对象,用
(2) 不可区分关系:设属性集
| $ I_{\rm{P}} = \{ x_i, x_j \in {\mathit{\boldsymbol{U}}}|\forall p \in {\mathit{\boldsymbol{P}}}, p(x_i ) = p(x_j )\} $ | (1) |
不可区分关系的含义是
(3) 上近似、下近似:上近似是指决策表中所有可能包含属性集合
| $ \overline P ({\mathit{\boldsymbol{X}}}) = \cup ({\mathit{\boldsymbol{Y}}} \in U/I_{\rm{P}}:{\mathit{\boldsymbol{Y}}} \cap {\mathit{\boldsymbol{X}}}\ne \emptyset ) $ | (2) |
| $ \underline P ({\mathit{\boldsymbol{X}}}) = \cup ({\mathit{\boldsymbol{Y}}} \in U/I_{\rm{P}}:{\mathit{\boldsymbol{Y}}} \subseteq {\mathit{\boldsymbol{X}}}) $ | (3) |
(4) 属性约简:在知识系统
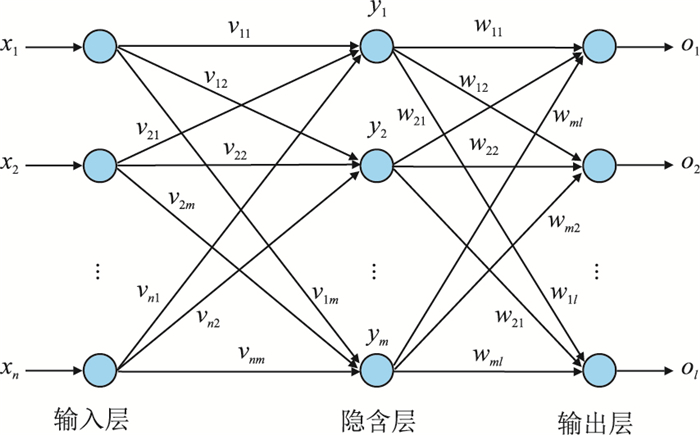
BP神经网络模型是由一个输入层、一个输出层以及一个或多个隐层共同构成的前馈神经网络[11],其中输入层的每个神经元与隐含层中的所有神经元相连接,隐含层中的每个神经元与输出层的神经元相连接,且同一层神经元之间不能连接[12]。网络的输入信号由输入层神经元节点传递给相邻的隐含层,经隐含层的神经元节点处理后传递到输出层,再经过输出层神经元节点处理后,最终输出结果[13]。BP神经网络的训练过程是通过误差反向传播算法来实现的,因此,也称BP网络为误差反向传播神经网络。图 1所示为具有单隐层的三层BP神经网络的结构图。
 |
| 图1 三层BP神经网络结构图 Fig. 1 The structure of three-layer BP neural network |
在图 1的网络结构中,输入层的神经元节点个数为
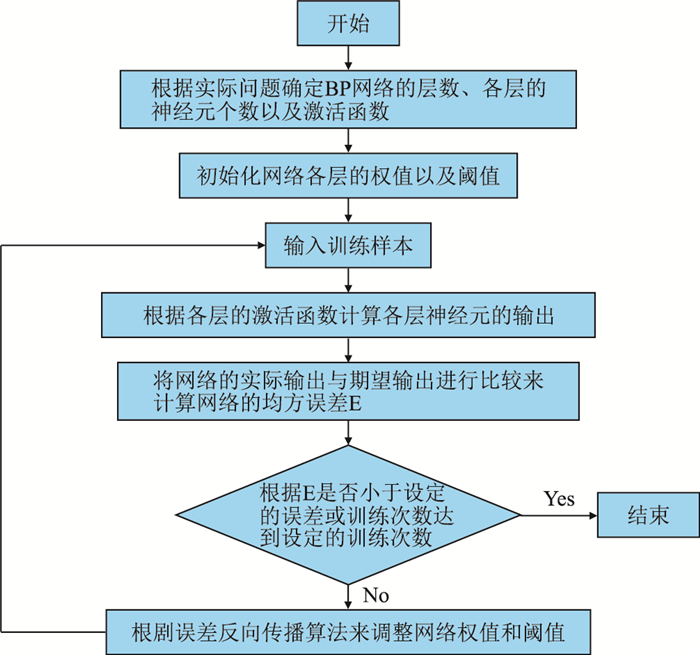
BP神经网络的学习过程包含信号的正向传递和误差的反向传播两个阶段[14]。在正向传递阶段,网络输入样本由输入层经过隐含层处理传送到输出层,经过输出层计算后得到网络的输出结果,然后将计算得到的输出结果与期望输出进行对比,如果网络输出结果与期望输出的差别太大,那么学习过程就进入误差的反向传播阶段。在误差的反向传播阶段,主要是把网络的总体误差经隐含层向输入层传递,将网络总体误差分摊给各层神经元节点,调整各层神经元节点之间的连接权值,当权值调整完成后,再次转到正向传递阶段。BP网络的整个学习或训练过程就是信号正向传递和误差反向传播的迭代过程,直到整个网络均方误差值在设定的误差范围内或训练迭代次数达到指定次数时,整个网络的学习或训练过程结束。如图 2所示为BP神经网络训练过程的示意图。
 |
| 图2 BP神经网络的训练过程 Fig. 2 The training process of BP neural network |
本文的研究是基于实验室和某钻井公司合作开发的“安全监管预警系统”项目,并通过对作业现场的实地考察,在辨识并统计了钻井过程中影响作业安全因素的基础上,根据相关研究成果,从人的不安全行为和物的不安全状态两个方面考虑构建了影响钻井作业现场安全的指标体系[15-16]。该指标体系体现了影响作业现场安全的相关因素,并将评价指标划分为3层。表 1为构建的3层评价指标体系。
| 表1 某钻井公司的钻井作业安全评价指标体系 Table 1 Drilling safety assessment system of a drilling company |
因为表 1中隐患或违章因素可能会对作业现场各个施工阶段带来各种各样风险,甚至引发事故,最终可能会对施工作业人员造成不同程度的伤害。因此根据对作业人员造成的伤害程度来定义钻井作业安全状态等级,并将安全状态等级划分为四类:无伤亡、轻伤、重伤、死亡。
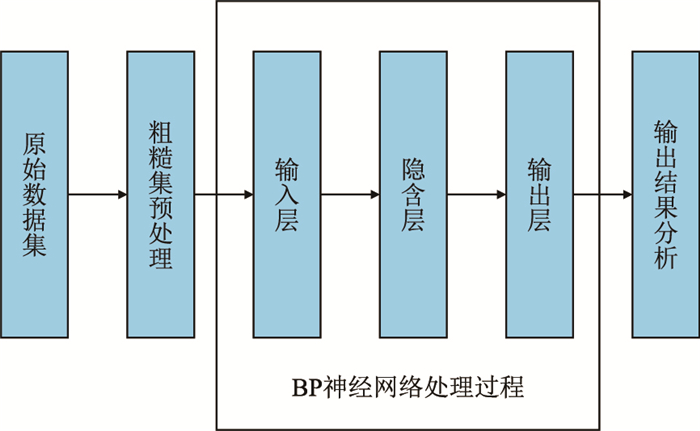
2.2 钻井作业安全评价模型本文将粗糙集和BP神经网络结合起来构建安全评价模型对钻井作业现场的安全进行监管,粗糙集主要用来构建评价模型的前置系统,对通过构建的安全评价指标体系统计得到的数据做属性约简,去除数据中的冗余或噪声因素,根据约简结果来构建BP神经网络的输入层和输出层,并根据输入层和输出层神经元的个数采用试凑法来构建网络的隐含层,然后采用根据约简结果构建的训练数据和测试数据对建立的BP神经网络进行训练和测试,保证安全评价模型的可靠性。图 3所示为构建的安全评价模型结构示意图。
 |
| 图3 钻井作业安全评价模型 Fig. 3 The safety assessment model of drilling operation |
粗糙集和BP神经网络相融合的钻井作业安全评价模型的构建任务主要分为两个阶段:使用粗糙集对数据集的预处理阶段和根据约简结果构建BP神经网络。
(1) 基于粗糙集的数据预处理
通过粗糙集理论能够完成决策表的完备化、离散化、属性约简、规则提取以及数据统计等操作[17]。本文主要通过实验室实际项目中的粗糙集模块对根据指标体系构建的数据集进行离散化以及对离散化后的数据进行属性约简。
(2) BP神经网络的构建
在BP神经网络中,隐含层的个数与网络的性能不是正相关关系,隐含层越多会导致网络的训练时间直线上升,因为1个隐含层的BP神经网络已经具有相当强大的非线性映射能力,所以本文构建的安全评价模型使用的是只有1个隐含层的网络结构。1个隐含层的BP神经网络构建主要包括了确定输入层神经元的个数、隐含层神经元的个数、输出层神经元的个数以及激活函数的选取。
① 输入层神经元的个数
确定输入层神经元个数主要是通过粗糙集对原数据集的预处理阶段完成的,约简后得到的集合中元素的数量就可以作为输入层的神经元数量。
② 输出层神经元的个数
输出层神经元的输出结果最终需要和具体案例中的实际结果进行对比,因此,在设计输出层神经元的时候需要以具体案例中的实际结果为基础。BP网络常用的激活函数是Sigmoid函数[18],因为该函数的值域是(0,1),所以常用0或1来表示输出层神经元的输出结果。本文2.1节中将安全状态等级分为四类,因此将输出层神经元的个数设置为4个,其中1000表示无伤亡,0100表示轻伤,0010表示重伤,0001表示死亡。
③ 隐含层神经元的个数
关于隐含层神经元节点个数的获取还不存在比较成熟的方法,常用的设置隐含层神经元节点个数方法是试凑法,即先设定较少的神经元数量,逐渐增多神经元的数量,最后,采用同一个学习样本对不同的网络模型进行训练,选取网络总体误差最小的模型中隐含层神经元的数量作为所建立模型的隐层结点的数量。在采用试凑法时,可以使用经验公式
本文的样本数据来源于2014-01-01至2015-09-19项目风险数据库中对三级指标在当天的发生次数进行统计,以及当天的事故复杂情况。表 2所示为构建的样本数据集,其中最后一列D表示当天的安全情况,1,2,3,4分别与安全评价模型中的输出1000,0100,0010,0001相对应,依次表示无伤亡,轻伤,重伤,死亡。
| 表2 原始样本数据 Table 2 The original sample data |
因为粗糙集不能分析连续性数据[19],得到原始样本数据后,首先用实验室实际项目中的粗糙集模块对数据进行离散化操作,表 3为离散化后的结果。
| 表3 2014年原始样本数据离散化后的结果 Table 3 The discrete result of original sample data in 2014 |
然后对2014年离散化后的数据进行属性约简寻找最小约简集,常用的约简方法有基于遗传算法的约简与Johnson算法[20],本文分别使用这两种约简算法对2014年离散化后的数据进行约简,表 4和表 5为所得到的约简结果,根据表 4和表 5能够得到影响钻井作业现场安全指标因素所组成的最小属性集是{C3,C4,C10,C12,C20,C22,C23,C25,C26},属性集中元素的个数为9。通过现场反馈,约简得到的9个指标因素比较符合实际情况。
| 表4 基于遗传算法的约简结果 Table 4 Reduction results based on GA |
| 表5 基于Johnson算法的约简结果 Table 5 Reduction results based on Johnson |
根据得到的最小约简集中指标因素数量,本文将BP网络中输入层节点数量设置为9,2.2节中已经讨论了将输出层节点的数量设置为4,根据经验公式得到隐层节点的数量范围为6~24。
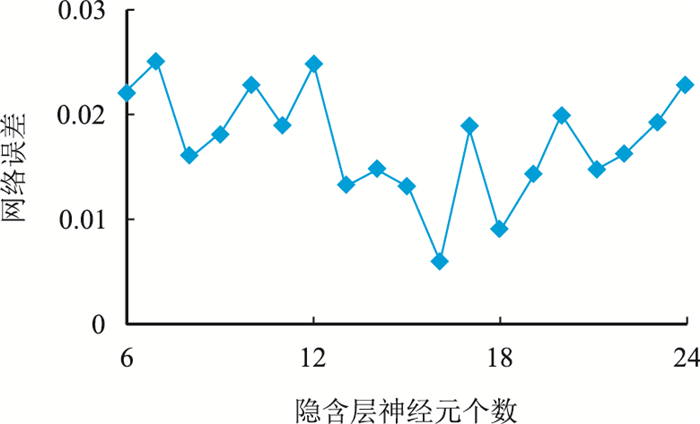
根据隐含层神经元节点数量范围建立不同的模型,然后采用从表 2中选取2014年数据中的200 d训练数据对网络进行训练,在网络收敛后,比较不同网络模型的总体误差,选取误差值最小的网络模型中隐含层节点个数作为最终建立的安全评价模型中隐层节点的个数。图 4为隐含层神经元个数与网络误差的关系。从图中可以得到当隐含层神经元的数量为16时,对应网络的整体误差值最小为0.006。因此本文将安全评价模型的隐层节点数量设为16。
 |
| 图4 网络误差与隐含层神经元个数的对应关系图 Fig. 4 The relationship between network error and the number of hidden layer neuron |
在隐层节点数量设置为16后,使用训练数据对构建的BP神经网络进行学习,当网络总体误差小于或等于既定的误差值或网络的训练迭代次数大于所设置的迭代次数时,保存此时网络各层的神经元节点间的连接权重值,并结束训练过程。如图 5所示为网络的训练性能曲线,从图中可以看出迭代次数为30时,网络的均方误差最小,此时网络的性能最好。
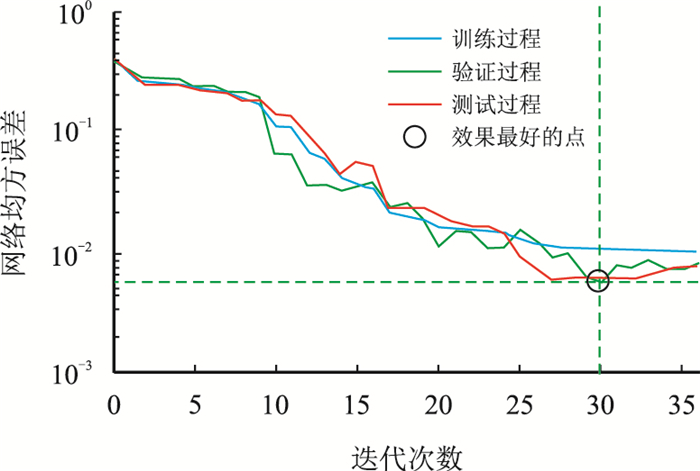 |
| 图5 BP神经网络训练过程的性能曲线 Fig. 5 The performance curve of neural network training process |
图 6所示为网络训练过程中对学习样本识别能力的混淆矩阵。4个混淆矩阵(confusion matrix)分别表示训练过程对样本的识别能力,验证过程对样本的识别能力,测试过程的识别能力以及网络总体识别能力,以训练混淆矩阵为例,来简述图 6中部分单元格的含义,其中前4列中前4行表示目标类和输出类的匹配个数以及匹配数在样本中的覆盖率,第5行则代表模型对每个目标类的识别率,第5行第5列的数据表示模型对4类目标的整体识别率。从图中可以看出,在训练阶段,网络对学习样本的识别正确率为86.5%;在验证阶段,对验证样本的识别正确率为91.3%;在测试阶段,对测试样本的识别正确率为87.0%;网络的整体识别率达到了87.3%。
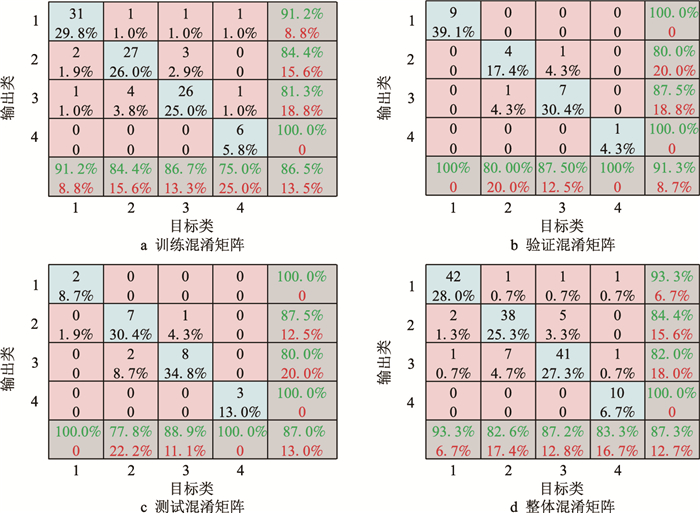 |
| 图6 BP神经网络训练的混淆矩阵 Fig. 6 The confusion matrix of BP neural network's training |
为验证模型的可行性,从2015-01-01到2015-09-19的数据中,选取16 d的数据记录作为测试样本对模型进行验证,其中,选取的记录中无伤亡、轻伤、重伤以及死亡4种状态各占1/4,表 6所示为根据约简结果选取的16 d测试样本数据。
| 表6 测试样本 Table 6 Testing samples |
将测试样本数据输入到建立的BP神经网络模型中,根据网络模型计算出16 d数据的输出值,并与当天安全情况所对应输出值进行对比,其中当天安全情况所对应的输出值为1000(无伤亡)、0100(轻伤)、0010(重伤)以及0001(死亡),表 7为网络输出值与实际情况的对比结果,从表 7可以看出16 d的测试数据中有14 d的网络输出值与实际情况是一致的,另外2 d的网络输出与实际结果不匹配,其中2015-08-20当天的安全情况为0001(死亡),网络的输出结果为轻伤,2015-09-18的实际值为0100(轻伤),网络的输出结果为重伤,使用测试样本对模型进行测试的正确率达到87.5%,根据与现场工作人员进行沟通得到的反馈信息表明运用该模型对钻井作业现场进行安全评估是可行的。
| 表7 神经网络的预测值 Table 7 The forecast result of neural network |
(1) 通过对钻井作业现场出现的违章和隐患进行分析,从人和物两个方面考虑构建了影响作业现场安全的三层指标体系。
(2) 以项目风险数据库中第三级指标的当天发生次数以及当天的事故情况为基础构建了原始数据集,并采用粗糙集软件对数据集进行约简,减少了BP神经网络的输入。
(3) 根据约简结果以及作业现场当天的安全情况完成了BP神经网络输入层和输出层的设计,并结合经验公式得到隐含层节点的数量范围在6~24。对比不同隐含层所对应网络的整体误差,将网络模型中隐含层节点个数设置为16。
(4) 从2014年的数据中选取了200 d的记录对建立的网络模型进行训练,待模型训练完成后,又从2015-01到2015-09的数据中选取了16 d的数据对模型进行验证,结果表明,模型的准确性可以满足钻井作业现场的安全评价要求。
| [1] | 中国石油天然气集团公司质量安全环保部. HSE风险管理理论与实践[M]. 北京: 石油工业出版社, 2009. |
| [2] |
刘菊梅, 王宏图, 李文华, 等. 陆上油气钻井作业评价指标体系的构建[J].
油气田地面工程, 2009, 28(8): 28–29.
LIU Jumei, WANG Hongtu, LI Wenhua, et al. Building of Onshore oil and gas drilling evaluation system[J]. OilGasfield Surface Engineering, 2009, 28(8): 28–29. doi: 10.3969/j.issn.1006-6896.2009.08.015 |
| [3] |
刘菊梅, 龙政军, 王宏图, 等. 陆上油气钻井作业安全评价模型探索[J].
石油天然气学报, 2010, 32(2): 112–116.
LIU Jumei, LONG Zhengjun, WANG Hongtu, et al. Study on safety evaluation model of oil and gas drilling operation[J]. Journal of Oil and Gas Technology, 2010, 32(2): 112–116. doi: 10.3969/j.issn.1000-9752.2010.02.026 |
| [4] |
苏义脑, 陈烨, 闫铁, 等. 气体钻井钻头泥包风险预测及影响因素研究[J].
天然气工业, 2016, 36(6): 60–65.
SU Yinao, CHEN Ye, YAN Tie, et al. Risk prediction of bit balling in gas grilling and its ijfluential factors[J]. Natural Gas Industry, 2016, 36(6): 60–65. doi: 10.3787/j.issn.1000-0976.2016.06.009 |
| [5] | VINNEM J, SELJELID J, HAUGEN S, et al. Generalized methodology for operational risk analysis of offshore installations[J]. Proceedings of the Institution of Mechanical Engineers, Part O:Journal of Risk and Reliability, 2008, 223(1): 87–97. doi: 10.1243/1748006XJRR109 |
| [6] | SAATY T L. Decision making with the analytic hierarchy process[J]. International Journal of Services Sciences, 2008, 1(1): 83–98. doi: 10.1504/IJSSCI.2008.017590 |
| [7] | HUANG K, CHEN S F. Study and implementation on the grey comprehensive evaluation support system of ecocity[J]. Journal of Southeast University (English Edition), 2002, 18(4): 356–360. |
| [8] |
张文修, 吴伟志. 粗糙集理论介绍和研究综述[J].
模糊系统与数学, 2000, 14(4): 1–12.
ZHANG Wenxiu, WU Weizhi. An introduction and research review of rough set theory[J]. Fuzzy Systems and Mathematics, 2000, 14(4): 1–12. doi: 10.3969/j.issn.1001-7402.2000.04.001 |
| [9] | PAWLAK Z. Rough sets[J]. Communications of ACM, 1995, 38(11): 89–95. doi: 10.1145/219717.219791 |
| [10] | PAWLAK Z. Rough set-theoretical aspects of reasoning about data[M]. Dordrecht: Kluwer Academic Publishers, 1991. |
| [11] |
马海纬, 杜慧. 基于粗糙集和BP神经网络的钻井作业安全事故预测[J].
内江科技, 2015, 36(4): 51–52, 74.
MA Haiwei, DU Hui. The prediction of drilling accidents based on rough set and bp neural network[J]. Neijiang Science and Technology, 2015, 36(4): 51–52, 74. |
| [12] |
苏伟, 刘景双, 李方. BP神经网络在水资源承载能力预测中的应用[J].
水利水电技术, 2007, 38(11): 1–4.
SU Wei, LIU Jingshuang, LI Fang. Application of BP neural network in prediction of carrying capacity of water resources[J]. Water Resources and Hydropower Engineering, 2007, 38(11): 1–4. doi: 10.3969/j.issn.1000-0860.-2007.11.001 |
| [13] |
陈小前, 罗世彬, 王振国, 等. BP神经网络应用中的前后处理过程研究[J].
系统工程理论与实践, 2002, 22(1): 65–70, 88.
CHEN Xiaoqian, LUO Shibin, WANG Zhenguo, et al. Research on preprocessing and postprocessing of the application of BP neural network[J]. Systems Engineering Theory and Practice, 2002, 22(1): 65–70, 88. doi: 10.3321/j.issn:1000-6788.2002.01.010 |
| [14] | DING S, JIA W, SU C, et al. An improved BP neural network algorithm based on factor analysis[J]. Journal of Convergence Information Technology, 2010, 5(4): 103–108. doi: 10.4156/jcit.vol5.issue4.11 |
| [15] |
郭杰. 钻井施工现场风险源分析与风险控制措施[J].
内蒙古石油化工, 2010(20): 31–33.
GUO Jie. Drilling construction site risk source analysis and risk control measures[J]. Inner Mongolia Petrochemical Industry, 2010(20): 31–33. doi: 10.3969/j.issn.1006-7981.2010.20.014 |
| [16] |
王兵, 杨小莹, 赵春兰, 等. 基于贝叶斯网络的钻井作业现场风险评估[J].
西南石油大学学报(自然科学版), 2015, 37(2): 131–137.
WANG Bing, YANG Xiaoying, ZHAO Chunlan, et al. Drilling site risk assessment based on bayesian network[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(2): 131–137. doi: 10.11885/-j.issn.1674-5086.2014.09.01.02 |
| [17] | ØHRN A, KOMOROWSKI J. Rosetta-a rough set toolkit for analysis of data[C]//Third International Joint Conference on Information Sciences, 1997. |
| [18] | 从爽. MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术出版社, 2003: 55-70. |
| [19] |
沈永红, 王发兴. 基于信息熵的粗糙集属性离散化方法及应用[J].
计算机工程与应用, 2008, 44(5): 221–224.
SHEN Yonghong, WANG Faxing. Method of attributes discretization in rough sets using information entropy and its application[J]. Computer Engineering and Applications, 2008, 44(5): 221–224. doi: 10.3778/j.issn.1002-8331.-2008.05.070 |
| [20] |
任永功, 王杨, 闫德勤. 基于遗传算法的粗糙集属性约简算法[J].
小型微型计算机系统, 2006, 27(5): 862–865.
REN Yonggong, WANG Yang, YAN Deqin. Rough set attribute reduction algorithm based on GA[J]. Mini-Micro Systems, 2006, 27(5): 862–865. doi: 10.3969/j.issn.1000-1220.2006.05.022 |
 2017, Vol. 39
2017, Vol. 39


