2. 中海石油(中国)有限公司湛江分公司, 广东 湛江 524057
2. Zhanjiang Branch Co. Ltd., CNOOC, Zhanjiang, Guangdong 524057, China
在油气勘探和开发过程中,带封隔器的完井管柱在注水、生产、酸化压裂等施工过程中都起着重要的作用[1-2]。由于在井的生命周期中,井下工况时有变更,井筒温度场和压力场也随之改变,从而导致封隔器管柱所受载荷发生变化或管柱发生形变[3-7]。如果井筒密封腔内的封隔器可以自由移动,就有可能导致密封段移出密封腔,造成封隔器上下窜通;若封隔器不能移动或仅能有限移动时,就可能使其中心管发生塑性变形导致断裂,更严重时可能造成封隔器在井筒内无法起出。因此,针对高温高压井,研究和分析封隔器管柱上压力和温度变化所引起的各种效应是十分必要的[8-13]。
对于带封隔器的完井管柱受力分析,目前对单封隔器结构的考虑较多,而对带多封隔器的完井管柱结构研究较少,但参考Norsok D010规范,在现场生产过程中为了提高井筒完整性,还可能需要在油管柱上配备多个封隔器。针对多封隔器复合管柱结构特点,研究了各种效应的影响,实例计算了井下作业工况的管柱的受力及变形情况。
1 力学分析模型管柱结构示意图见图 1,模型建立时,假设:
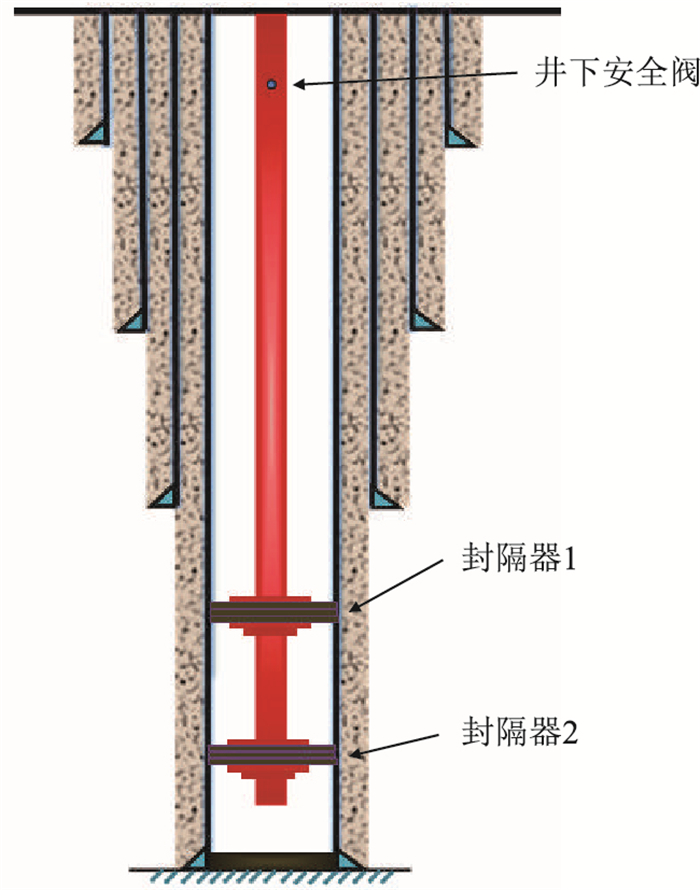 |
| 图1 多封隔器复合管柱结构示意图 Fig. 1 Structural diagram of combined pipe with multi-packer |
(1)封隔器管柱为多封隔器复合管柱;
(2)忽略管柱与井壁摩擦;
(3)井筒内存在液体;
(4)不考虑井内液体流动。
2 受力分析 2.1 端面效应在管柱直径变化处和管柱端面上,由于内外压力的作用,会产生端面效应。封隔器处的端面力为
| $ {F_{{\rm{a}}, m}}'={p_{{\rm{i}}, m}}\left({{A_{{\rm{sb}}, m}}-{A_{{\rm{i}}, m}}} \right)-{p_{{\rm{o}}, m}}\left({{A_{{\rm{sb}}, m}}-{A_{{\rm{o}}, m}}} \right) $ | (1) |
式中:Fa, m′-封隔器m处的端面力,N;
pi, m -封隔器m处的油管内压力,Pa;
po, m -封隔器m处的环空压力,Pa;
Asb, m-封隔器m密封腔截面积,m2;
Ai, m -封隔器m处的油管柱内截面积,m2;
Ao, m -封隔器m处的油管柱外截面积,m2;
下标m-封隔器编号,m=1, 2。
在管径变化处,还会存在集中的液压作用力,其大小为
| $ {F_{{\rm{a}}, n}}{\rm{'}}={p_{{\rm{i}}, n}}\left({{A_{{\rm{i}}, n+1}}-{A_{{\rm{i}}, n}}} \right)-{p_{{\rm{o}}, n}}\left({{A_{{\rm{o}}, n+1}}-{A_{{\rm{o}}, n}}} \right) $ | (2) |
式中:Fa, n′-油管柱变径n处的液柱压力,N;
pi, n-油管柱变径处n的油管内压,Pa;
po, n-油管柱变径处n的环空压力,Pa;
Ai, n-各级油管段的内截面积,m2;
Ao, n-各级油管段的外截面积,m2;
下标n-变径油管段编号。
对于单/多封隔器管柱的完井结构,其某一处的实际轴向载荷,是完井封隔器的端面力减去该位置下部油管柱在空气中的单位长度的重量。采用多封隔器复合管柱的完井结构时,也要考虑管柱之间液柱压力的影响。封隔器位置的轴向载荷为
| $ {F_{{\rm{a}}, m}}={F_{{\rm{a}}, m}}' $ | (3) |
式中:Fa, m-封隔器m处的实际载荷,N。
油管柱每个变径处的接触面所受的实际载荷为
| $ {F_{{\rm{a}}, n}}=\sum {F_{{\rm{a}}, n}}{\rm{'}}+{F_{{\rm{a}}, m}}{\rm{'}}+\sum {{W_{{\rm{s}}, n+1}}} {L_{n+1}} $ | (4) |
式中:Fa, n-油管柱n变径位置所受到的实际轴向力,N;
∑ Ws, n+1-油管段n+1在空气中的管体单位重量,N/m;
Ln+1-油管段n+1的长度,m;
如果油管柱内外的液体密度和井口压力发生变化,则会引起油套环空和油管内压力分布的改变,进而管柱的轴向力发生改变。
端面力变化会造成管体长度的变化,管体伸长为正值,管体缩短为负值,由虎克定律,有
| $ \Delta L_{1, {n}}=-\dfrac{L_n{\Delta F_{{\rm{a}}, n}}}{EA_n} $ | (5) |
式中:∆L1, n-管柱n伸长量,m;
∆Fa, n-管柱n实际力变化值,N;
Ln-油管段n的长度,m;
E-弹性模量,Pa;
An-管柱n的截面积,m2。
管柱总的伸长量为各级管柱伸长量之和
| $ \Delta L_1=\sum \Delta L_{1, n} $ | (6) |
式中:∆L1-管柱总的伸长量,m。
2.2 热胀冷缩效应开采过程中井筒温度分布会发生改变,引起管体的长度和轴向载荷发生变化,这种现象称为热胀冷缩效应。
当下入封隔器管柱时,按原始地层温度考虑长度变化;坐封油管柱时,油管柱的温度也认为等于原始地层温度。管柱坐封后,开采时温度场发生改变,从而导致油管柱发生热胀冷缩现象。
温度变化梯度是由井口和井底的初始、最终的温度决定,并且取每级管柱的平均温度
| $ \overline T_n=T_{\rm t}+0.5 \left(V_{{\rm D1}, n}+V_{{\rm D1}, n} \right)G_{\rm r} $ | (7) |
式中:Tn-管柱n的平均温度,℃;
Tt-井口温度,℃;
VD1, n-管柱n的上端面到井口的垂直距离,m;
VD2, n-管柱n的下端面到井口的垂直距离,m;
Gr-完井油管柱单位长度的温度变化量,℃/m。
油管柱的各级长度热胀冷缩效引起的变化量和总变化分别为
| $ \Delta {L_{2, n}}=\alpha {L_n}\Delta {T_n} $ | (8) |
| $ \Delta {L_2}=\sum \Delta {L_{2, n}} $ | (9) |
式中:∆L2, n-管柱n热胀冷缩效引起的变化量,m;
α-油管线膨胀系数,1/℃;
∆Tn-管柱n温度变化量,℃。
2.3 形变效应井筒内压力的改变将会导致油管径向力的变化,增加管柱内压,从而造成管柱直径增大,长度缩短(自由移动管柱);相反地,如果增加环空外压,油管柱直径会减小,同时长度增长(自由移动管柱),这种现象就是形变效应。
油管柱内外流体密度变化将导致油管柱长度的变化
| $ \Delta {L_{3, n}}'=-\frac{{\upsilon L_n^2}}{E} \cdot \frac{{\Delta {\rho _{{\rm{i}}, n}}-{{\left({\frac{{{d_{{\rm{o}}, n}}}}{{{d_{{\rm{i}}, n}}}}} \right)}^2}\Delta {\rho _{{\rm{o}}, n}}}}{{{{\left({\frac{{{d_{{\rm{o}}, n}}}}{{{d_{{\rm{i}}, n}}}}} \right)}^2}-1}} $ | (10) |
式中:∆L3, n′ -油管柱段n受密度变化影响的长度变化量,m;
ν-材料活塞比,一般取0.3;
∆ρi, n-油管柱段n内流体密度的变化量,kg/m3;
∆ρo, n-油管柱段n外环空流体密度的变化量,kg/m3;
do, n-油管柱段n外径,m;
di, n-油管柱段n内径,m。
油管柱内外流体压力变化也将导致油管柱长度的变化
| $ \Delta {{L}_{3, n}}''=-\frac{\upsilon L_{n}^{2}}{E}\cdot \frac{\Delta {{p}_{\text{i}, n}}-{{\left(\frac{{{d}_{\text{o}, n}}}{{{d}_{\text{i}, n}}} \right)}^{2}}\Delta {{p}_{\text{o}, n}}}{{{\left(\frac{{{d}_{\text{o}, n}}}{{{d}_{\text{i}, n}}} \right)}^{2}}-1} $ | (11) |
式中:∆L3, n" -油管柱受内外流体压力变化影响的长度变化量,m;
∆pi, n-油管柱段n内压力变化值,Pa;
∆po, n-油管柱段n外环空压力变化值,Pa。
总形变效应引起的油管柱的变化量∆L3为
| $ \Delta {{L}_{3}}=\sum{\Delta }{{L}_{3, n}}'+\sum{\Delta }{{L}_{3, n}}'' $ | (12) |
完井管柱采用多封隔器时,任一位置的虚载荷是当前封隔器处的虚载荷减去该断面以下各级管体液体中的重量。所以,当前封隔器处的虚载荷为
| $ F_{{\rm f}, m}=A_{{\rm sb}, m}\left(p_{{\rm i}, m} - p_{{\rm o}, m} \right) $ | (13) |
式中:Ff, m封隔器m处的虚载荷,N。
不同级管柱连接处虚载荷为
| $ \Delta F_{{\rm f}, n}=F_{{\rm f}, m} - \sum W_{\rm et} $ | (14) |
式中:∆Ff, n-管径变化处的虚载荷,N;
Wet-变径位置到封隔器的管体在液体中的重量,N。
相比于采用单一封隔器的情况,采用多封隔器时,完井管柱的中性点的位置更难以确定。如果完井管柱采用两个封隔器,假设中性点在上封隔器到井口之间,中性点位置计算公式为
| $ N=\frac{F_{\text{f},m}^{*}}{{{\left( {{w}_{\text{s}}}+{{w}_{\text{i}}}-{{w}_{\text{o}}} \right)}_{[2]}}} $ | (15) |
式中:N-中性点与井口的距离,m;
Ff, m*-封隔器阻隔而产生的虚载荷,N;
ws-管柱在空气中的单位长度的重量,N/m;
wi-管单位长度油管柱内液体(气体)的重量,N/m;
wo单位长度油管柱下入后排开液体的重量,N/m。
下标[2]-第二级油管柱。
若N值小于该管段的长度,则该级管柱存在中性点;若N值大于该管段的长度,则上部管段存在中性点
| $ N=\frac{F_{\text{f}, m}^{*}-{{L}_{2}}{{\left({{w}_{\text{s}}}+{{w}_{\text{i}}}-{{w}_{\text{o}}} \right)}_{[2]}}}{{{\left({{w}_{\text{s}}}+{{w}_{\text{i}}}-{{w}_{\text{o}}} \right)}_{[1]}}}+{{L}_{2}} $ | (16) |
式中:L2-第二级油管柱的长度,m;
下标[1]-第一级油管柱。
如果求出的N值小于这两段油管段长度之和,则中性点位于假设的油管段内,否则继续求中性点位置,如果N仍大于三级管段之和,则这三级管段均是完全屈曲。
油管段部分屈曲取决于中性点是否在该段上,若中性点位于该段,则其下油管段会出现完全屈曲,其上油管段不会发生屈曲,部分屈曲油管段的长度伸长量为
| $ \Delta {{L}_{4, n}}\text{ }\!\!'\!\!\text{ }=-\frac{r_{n}^{2}F_{\text{f}, n}^{2}}{8E{{I}_{n}}{{W}_{n}}} $ | (17) |
式中:∆L4, n′-部分屈曲油管段的长度伸长量,m;
rn-油管段n在径向上的间隙,m;
In-油管段n所受的惯性力矩,m4;
Wn-单位长度的油管段n在液体中的重量,N/m。
完全螺旋和正弦屈曲管段伸长量为
| $ \Delta {{L}_{4, n}}''=-\frac{r_{n}^{2}F_{\text{f}, n}^{2}}{8E{{I}_{n}}{{W}_{n}}}\frac{{{L}_{n}}{{W}_{n}}}{{{F}_{\text{f}, n}}}\left(2-\frac{{{L}_{n}}{{W}_{n}}}{{{F}_{\text{f}, n}}} \right) $ | (18) |
式中:
∆L4, n"完全屈曲油管段的长度伸长量,m;
螺旋和正弦屈曲效应引起的油管段伸长量∆L4的计算公式为
| $ \Delta {{L}_{4}}=\sum{\Delta }{{L}_{4, n}}\text{ }\!\!'\!\!\text{ }+\sum{\Delta }{{L}_{4, n}}'' $ | (19) |
如果在完井作业时下入机械式封隔器坐封,则需要在下入油管柱时利用地面施加的正向或负向下放力(压缩为正,拉伸为负)产生一定的坐封载荷来达到密封效果,然而该工况也会引起油管柱长度的变化。
下放力引起管柱长度的变化包括两个方面,一方面是根据虎克定律计算管柱的纯弹性增长,另一方面是屈曲的影响,计算公式分别为
| $ \Delta {{L}_{5, n}}'=\frac{{{F}_{\text{so}, n}}{{L}_{n}}}{{{A}_{n}}E} $ | (20) |
| $ \Delta {{L}_{5, n}}''=\frac{F_{\text{so}, n}^{2}r_{i}^{2}}{8E{{I}_{n}}{{\left({{w}_{\text{s}}}+{{w}_{\text{n}}}-{{w}_{\text{o}}} \right)}_{[n]}}} $ | (21) |
式中:∆L5, n′-受虎克定律影响的下放效应引起的长度变化量,m;
Fso, n-对应的下放力,N。
∆L5, n"-受屈曲影响的下放效应引起的长度变化量,m;
下标[n]-第n级油管柱。
对于复合管柱,虎克定律项叠加,屈曲项使用平均值
| $ \Delta {{L}_{5}}=\sum{\Delta }{{L}_{5, n}}'+\text{ }\frac{\sum{\Delta {{L}_{5, n}}''{{L}_{n}}}}{\sum{{{L}_{n}}}} $ | (22) |
多封隔器复合油管柱的总长度变化量∆L即为各种效应影响的综合
| $ \Delta L=\Delta L_1+\Delta L_2+\Delta L_3+\Delta L_4+\Delta L_5 $ | (23) |
式中:∆L-各种效应的总变形量,m。
2.7 总效应力假设管柱与封隔器不会出现相对位移,封隔器上力的变化量是根据油管柱内外压力和热胀冷缩效应来进行计算。假设油管柱的变形不会达到塑性变形,即可将利用长度变化值得到载荷的变化值。
由于多封隔器复合管柱各级油管段长度和截面积均不同,则需要对结果进行标准化
| $ R_{\rm AL}=\dfrac{\sum L_nA_n}{\sum L_n^2} $ | (24) |
式中:
RAL -标准化后的油管柱截面与长度之比,m。
效应力公式为
| $ \Delta F_{1-4}=\Delta L_{1-4}ER_{\rm AL} $ | (25) |
式中:∆F1-4-油管柱内外压力和热胀冷缩效应引起的载荷变化,N;
∆L1-4-油管柱内外压力和热胀冷缩效应引起的变形量,m。
3 实例计算某井使用双封隔器复合管柱进行生产,结构如图 2所示。其中封隔器1的胶筒直径为ϕ171.6 mm,垂深为5 100 m,封隔器2的胶筒直径为ϕ171.6 mm,垂深为5 718 m,其管柱受力及变形计算结果如表 1所示。
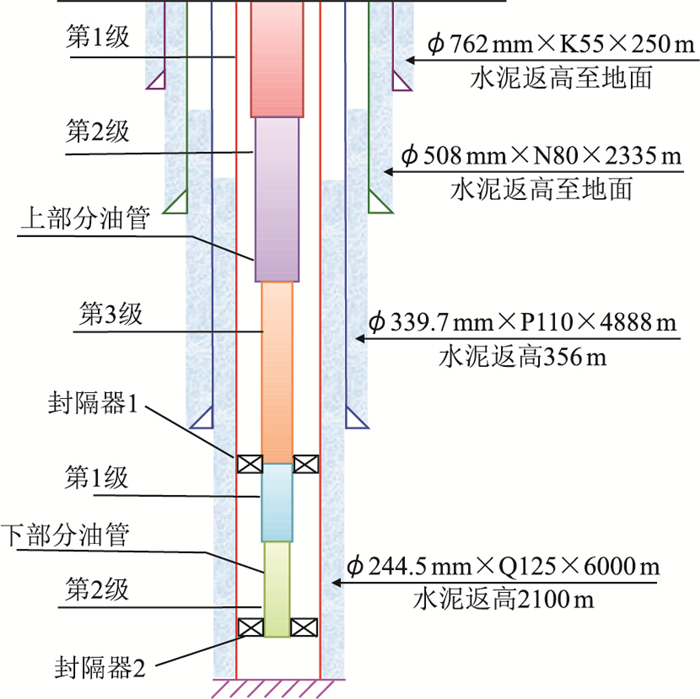 |
| 图2 实际管柱结构示意图 Fig. 2 Structural diagram of actual pipe |
| 表1 封隔器管柱的受力和变形计算结果 Table 1 Computational results of the force and deformation of packer string |
初始时刻,井口温度取16 ℃,产层处井内温度是130 ℃,油管内液体的密度1 078 kg/m3,油管外液体的密度1 078 kg/m3,油管压力和套管压力均为0。坐封后某一时刻井口温度为26.7 ℃,产层温度为130 ℃,油管内液体的密度为778 kg/m3,油管压力为13.8 MPa,套管压力为0,以该时刻为终点计算各效应的影响。
该油管柱分为上部分油管和下部分油管,活塞比为0.3,杨氏模量为207 GPa,热膨胀系数为0.0002332 ℃-1。上部分油管又分为1、2、3级,该部分第1级油管为ϕ139.7 mm (壁厚7.7 mm),单位长度油管的重量248.1 N/m,下入的垂深和测深均为610 m;该部分第2级油管为ϕ114.3 mm (壁厚6.9 mm),单位长度油管的重量183.9 N/m,下入的垂深和测深均为3 524 m;该部分第3级油管为ϕ88.9 mm (壁厚6.35 mm),单位长度油管的重量134.3 N/m,下入的垂深和测深均为5 100 m。下部分油管又分为1、2级,该部分第1级油管为ϕ88.9 mm (壁厚6.35 mm),单位长度油管的重量134.3 N/m,下入的垂深和测深均为5 400 m;该部分第2级油管为ϕ73 mm (壁厚5.5 mm),单位长度油管的重量118.5 N/m,下入的垂深和测深均为5 718 m。
3.1 封隔器中间距离对管柱变形量影响将封隔器2坐封位置固定为5 700 m,分别取封隔器1位置为5 100~5 300 m (间隔50 m)5种不同情况,封隔器之间相距400~600 m,保持其他参数不变。
图 3为上部分油管变形量与两封隔器间距关系曲线,可以看出上部管柱总变形量随封隔器之间距离的增大而减小,拉伸量的变化趋势逐渐减小,即封隔器1与井口的距离越小,轴向变形量越小、拉伸变化率越小。端面效应变形量随封隔器之间距离的增大而减小,拉伸量的变化趋势与总变形量几乎一致,而其余效应变形量为定值,随封隔器1与井口的距离越来越小,其温度的变化值越小,管内外的液柱压力值越小,因此这些效应的影响越不明明显。
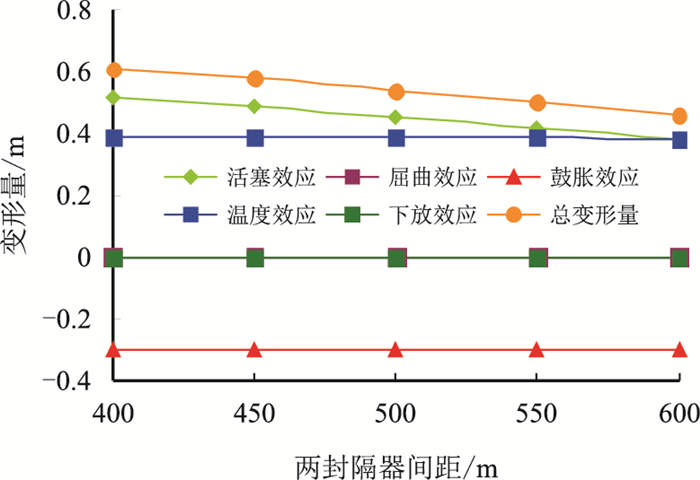 |
| 图3 上部分油管变形量同两封隔器间距关系曲线 Fig. 3 Relation curves between length deformation of upper tubing and distance of packers |
图 4为下部分油管变形量与两封隔器间距关系曲线,可以看出下部管柱总变形量随封隔器之间距离的增大而增大,压缩变化趋势逐渐增大,即封隔器1与井口的距离越大,管内外液柱压力增大,导致实际轴向载荷力和虚载荷均增大。端面效应和螺旋和正弦屈曲效应造成的压缩量均增加,形变效应造成的拉伸量增加。
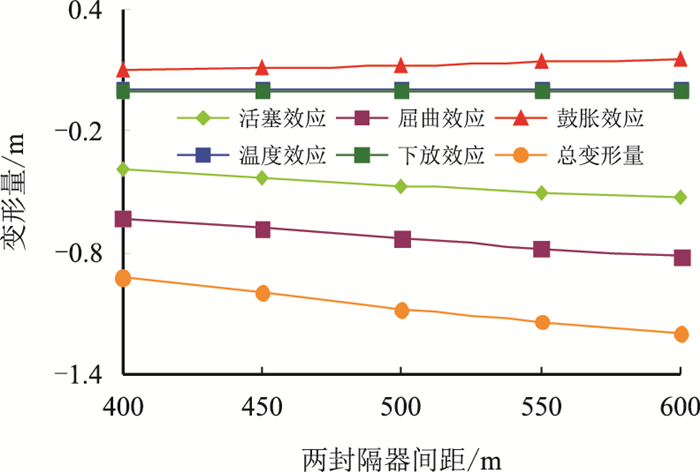 |
| 图4 下部分油管变形量同两封隔器间距关系曲线 Fig. 4 Relation curves between length deformation of lower tubing and distance of packers |
取油压为15~45 MPa (间隔10 MPa)4种不同情况,利用复合管柱计算模型,研究管柱总变形量随井口温度的变化趋势。
图 5为管柱总变形量同井口温度关系曲线。
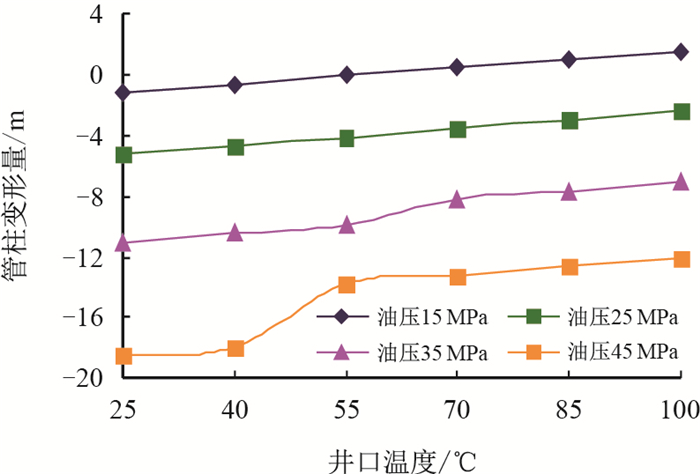 |
| 图5 管柱总变形量同井口温度关系曲线 Fig. 5 Relation curves between length deformation of tubing and wellhead temperature |
在给定油压条件下,管柱总轴向压缩量随井口温度增大而减小,管柱总轴向拉伸量随井口温度增大而增大,管柱拉伸变形趋势逐渐增大,管柱压缩变形趋势减小;在一定的井口温度条件下,管柱总轴向压缩量随油压增大而增大,轴向变形逐渐从拉伸变为压缩。当油压较低时,随着井口温度的增大,整个管柱的温度变化增加导致热胀冷缩效应加剧,而其他效应几乎无影响,所以管柱为拉伸变形;随着油压的增加,热胀冷缩效应产生足够的形变后,封隔器的阻隔作用会产生虚构载荷,导致管柱中性点位置改变,加速管柱变形;随着油压增大,端面效应、螺旋和正弦屈曲效应、形变效应作用更为明显,从而使管柱逐渐从拉伸演变为压缩。
4 结语(1)研究分析了高压气井多封隔器复合管柱的力学分析模型,研究了各种效应对封隔器管柱轴向变形的影响,并讨论了两封隔器间距以及温度、压力与管柱变形量的变化规律,为封隔器的设计的选择提供了参考,为实际工程运用提供了理论支撑。
(2))根据材料力学和弹塑性力学理论,推导出了弹性范围内虚拟长度变化转化为虚拟轴向力的一般公式。
(3)封隔器在井筒中的位置对整个管柱的受力和变形影响较大,井口温度和油压的变化也会直接影响管柱的变形量。准确模拟和预测多封隔器复合管柱的井下力学行为对确保井筒完整性具有重要指导意义。
| [1] |
张智, 周延军, 付建红, 等. 含硫气井的井筒完整性设计方法[J].
天然气工业, 2010, 30(3): 67–69.
ZHANG Zhi, ZHOU Yanjun, FU Jianhong, et al. A method of well integrity design for sour gas wells[J]. Natural Gas Industry, 2010, 30(3): 67–69. DOI:10.3787/j.issn.1000-0976.2010.03.017 |
| [2] | LOGINOV A. Plug and abandonment applications for inflatable packers in the gulf of Mexico, USA[C]. SPE 23923, 2013. doi:10.4043/23923-MS |
| [3] |
张智, 顾南, 杨辉, 等. 高含硫高产气井环空带压安全评价研究[J].
钻采工艺, 2011, 34(1): 42–44.
ZHANG Zhi, GU Nan, YANG Hui, et al. Safety evaluation on sustained casing pressure (SCP) in high-sulfur highproduction gas well[J]. Drilling & Production Technology, 2011, 34(1): 42–44. DOI:10.3969/j.issn.1000-768X.2011.01.014 |
| [4] |
李钦道, 谢光平, 张娟. 初始管柱压缩量计算分析--封隔器管柱受力分析系统讨论之三[J].
钻采工艺, 2001, 24(6): 48–51.
LI Qindao, XIE Guangping, ZHANG Juan. Calculation analysis of initial amount of compression of test string[J]. Drilling & Production Technology, 2001, 24(6): 48–51. DOI:10.3969/j.issn.1006-768X.2001.06.017 |
| [5] |
杨魁.同井注采封隔器设计及管柱力学分析[D].青岛:中国石油大学(华东), 2011.
YANG Kui. Packer design and mechanical analysis of injection-production string in one well[D]. Qingdao:China University of Petroleum, 2011. http://industry.wanfangdata.com.cn/sh/Detail/Thesis?id=Thesis_Y1876035 |
| [6] |
许建国. 带多封隔器水平井作业管柱解封力分析[J].
石油机械, 2011, 39(10): 69–71.
XU Jianguo. An analysis of the releasing force of the multi-packer horizontal-well operation string[J]. Petroleum Machinery, 2011, 39(10): 69–71. DOI:10.16082/j.cnki.issn.1001-4578.2011.10.019 |
| [7] |
赵晓伟, 牛彩云, 朱洪征, 等. 单封隔器抽油管柱受力变形分析[J].
石油矿场机械, 2011, 40(12): 51–54.
ZHAO Xiaowei, NIU Caiyun, ZHU Hongzheng, et al. Analysis of the deformation to the pump strings with the packer[J]. Oil Field Equipment, 2011, 40(12): 51–54. DOI:10.3969/j.issn.1001-3482.2011.12.013 |
| [8] |
郎学军, 李兴应, 刘通义, 等. 双封隔器分层压裂工艺技术研究与应用[J].
钻采工艺, 2004, 27(3): 45–47.
LANG Xuejun, LI Xingying, LIU Tongyi, et al. Research and application of separate zone fracturing with dual packer[J]. Drilling & Production Technology, 2004, 27(3): 45–47. DOI:10.3969/j.issn.1006-768X.2004.03.015 |
| [9] |
柴国兴, 刘松, 王慧莉, 等. 新型水平井不动管柱封隔器分段压裂技术[J].
中国石油大学学报(自然科学版), 2010, 34(4): 141–144.
CHAI Guoxing, LIU Song, WANG Huili, et al. New single-trip staged fracturing technology with packer isolation in horizontal wells[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(4): 141–144. DOI:10.3969/j.issn.1673-5005.2010.04.028 |
| [10] |
崔玉海, 唐高峰, 丁晓芳, 等. 注水管柱中温度效应的分析与计算[J].
石油钻采工艺, 2003, 25(2): 50–53.
CUI Yuhai, TANG Gaofeng, DING Xiaofang, et al. Analysis and calculation of the temperature effect in the water injection string[J]. Oil Drilling & Production Technology, 2003, 25(2): 50–53. DOI:10.3969/j.issn.1000-7393.2003.02.014 |
| [11] |
张智, 张琳琳. 高温高产气井自由套管热应力研究[J].
安全与环境学报, 2015, 15(4): 98–102.
ZHANG Zhi, ZHANg Linlin. Thermal stress model for the free-casing section to be used for high-temperature and high-yield gas wells[J]. Journal of Safety and Environment, 2015, 15(4): 98–102. DOI:10.13637/j.issn.1009-6094.2015.04.021 |
| [12] | ZHANG Z, WANG H. Sealed annulus thermal expansion pressure mechanical calculation method and application among multiple packers in HPHT gas wells[J]. Journal of Natural Gas Science and Engineering, 2016, 31: 692–702. DOI:10.1016/j.jngse.2016.03.091 |
| [13] |
张智, 王汉. 油套管导热系数与温度耦合模型计算井筒温度场[J].
中国科技论文, 2015, 10(21): 2539–2544.
ZHANG Zhi, WANG Han. A coupled model of wellbore temperature calculation between temperature and thermal conductivity of tubing and casing[J]. China Science Paper, 2015, 10(21): 2539–2544. DOI:10.3969/j.issn.2095-2783.2015.21.015 |
 2016, Vol. 38
2016, Vol. 38


