水平井技术以低成本、高产能等特点,广泛应用于油气藏开发,但由于水平井段井身结构的特殊性,井斜角位移较大,常规携岩过程中容易形成岩屑床,造成井眼清洗困难,井眼净化效果不好,可能导致严重的钻井事故。因此,基于分流继能机理[1-3],提出一种新的携岩方法即脉冲携岩。在脉冲携岩条件下,得到各参数对岩屑运移的影响规律。这对于合理设计钻井参数以及保证安全、优质、快速钻进有重要意义。
1 脉冲携岩数值模型 1.1 脉冲携岩简介钻井实践证明,提高井底水力冲击力,可以提高钻井速度,降低成本。在相同条件下,水锤效应使岩石受到脉冲射流的冲击压力要高出连续射流冲击压力很多倍。故脉冲射流是积蓄能量,在极短的时间内把能量传递给流体,并将流体发射出去,并以一定频率持续发射[4-8]。
在脉冲射流破岩机理的启发下,试探性地提出脉冲携岩想法,脉冲携岩即是周期性发射钻井液携带岩屑运移并冲击岩屑床这一过程。
1.2 物理模型及边界条件建立6"(1"=2.54 cm)井眼偏心环空物理模型如图 1所示。该模型采用一部分钻杆管柱串进行模拟研究。其中,钻杆采用API钻杆2根,单根长度9.0 m;环空内径88.9 mm、外径152.4 mm。采用结构化六面体网格进行网格划分,并对壁面附近的网格进行了局部的加密,如图 2所示。
 |
| 图1 6"井眼偏心环空流场模型 Fig. 1 Flow model of eccentric annulus with 6" hole |
 |
| 图2 6"井眼偏心环空网格划分 Fig. 2 Meshing of eccentric annulus with 6" hole |
泥浆钻井可视为不可压缩紊流流动,模拟时入口排量取15 L/s,环境压力29.3 MPa,井壁和钻柱按无滑移固定壁面边界条件设置。
1.3 脉冲参数引入脉冲电压波形6个脉冲波的参数定量描述脉冲携岩波形[9],如图 3所示(Um-脉冲幅度,m/s;tw -脉冲宽度,s;T-脉冲周期,s;q-占空比,无因次);6个参数分别为:(1)脉冲幅度Um:脉冲的最大值与最小值之差称为脉冲幅度;(2)脉冲宽度tw:脉冲峰值的持续期;(3)脉冲周期T:单个脉冲持续时间;(4)占空比q:指脉冲宽度与脉冲周期T的比值,有
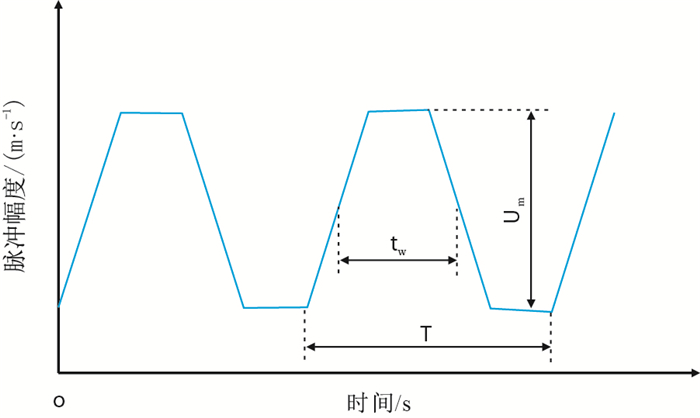 |
| 图3 脉冲携岩波形图 Fig. 3 Oscillogram of carrying rock by pulse wave |
另外,定义脉冲幅度比为脉冲峰值或脉冲谷值与脉冲平均值之差与脉冲平均值的比值百分比,定义占空比比例为脉冲宽度和脉冲周期与脉冲宽度之差的比值。
2 脉冲参数敏感性分析根据分流继能机理,脉冲携岩能量分配比的范围为0~15 %,其脉冲中携岩能量为0即为常规携岩形式;脉冲频率范围为4~50 Hz,即脉冲携岩的周期范围为0.02~0.25 s;根据携岩工具和水利脉冲发生器等工具旋转特性,确定占空比范围0.5~0.8,占空比取1:1,2:1,3:1,4:1。
首先寻找周期,在0.02~0.25 s这个区间内,由0.02 s开始,每隔0.02 s设置一个周期点,脉冲幅度比取为10%,占空比取1:1,2:1,3:1,4:1,采用两层水力模型作为研究对象,观察时间为15 s,评价标准为岩屑床移动距离和移动岩屑床速度。数值模拟中初始岩屑床设置如下:岩屑床长度为400.00 mm,岩屑床高度15.24 mm,岩屑床浓度80%。计算结果如图 4所示,其中黑色虚线为常规携岩两层水力模型岩屑床移动距离,可知在周期区间为0.14~0.18 s岩屑床移动距离最大,采用二分法继续对周期区间细化取值。
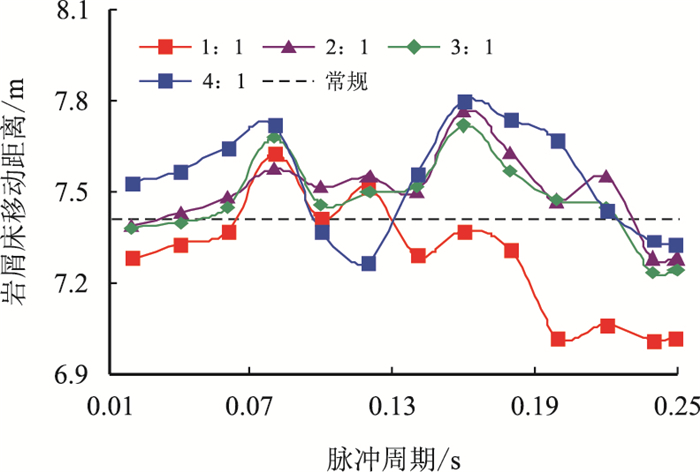 |
| 图4 脉冲周期初选 Fig. 4 Forward selection of the pulse period region |
采用二分法对周期区间细化取值的计算结果如图 5,可知在脉冲周期为0.15 s、占空比比例为3:1时,岩屑床移动距离最大,由此判定T=0.15 s为最佳周期。
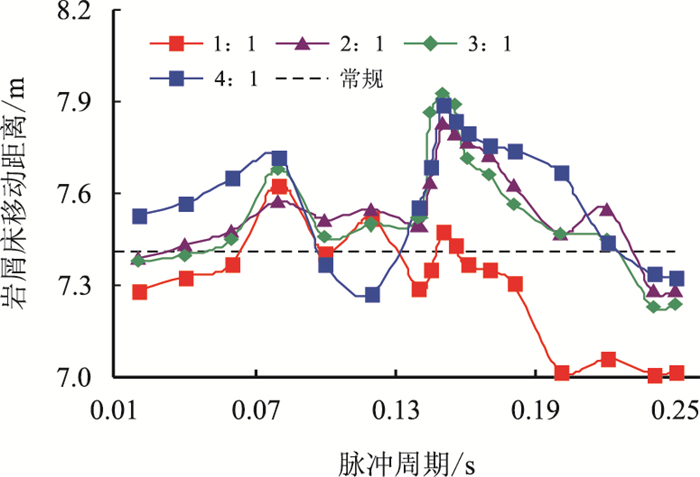 |
| 图5 细化周期区间 Fig. 5 Refinement of the pulse period region |
为验证T=0.15 s为最佳周期这一结论,对不同脉冲幅度比的情况进行计算,如图 6所示。
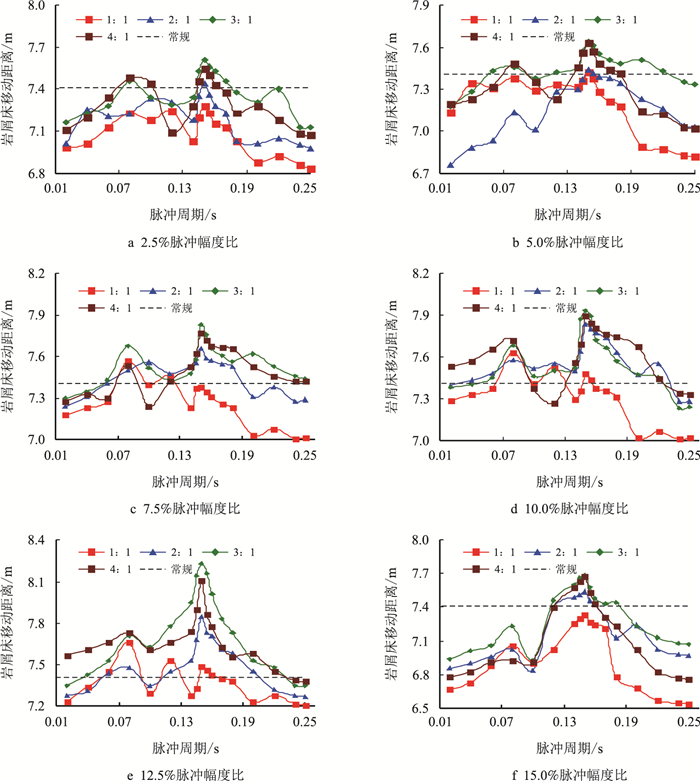 |
| 图6 不同脉冲幅度比时脉冲周期与岩屑床移动距离关系图 Fig. 6 Graph of pulse period and distance of cuttings bed movement with different pulse amplitude ratio |
由图 6可知:不同的脉冲幅度比情况下,每一种占空比在不同脉冲周期的岩屑床运移距离规律是一样的。在占空比比例为1:1时,随着脉冲周期的增大,岩屑床移动距离也逐渐增大,期间在T=0.08,T=0.12,T=0.15 s时处于峰值状态,然后逐渐减小,比较这3个时刻的岩屑床运移距离,在不同脉冲幅度比下都是不同的,大部分都没有超过常规携岩岩屑床移动距离7.41 m,1:1的岩屑床移动效果也不如其他比例。占空比为3:1和4:1时,随着脉冲周期的增大,岩屑床移动距离也逐渐增大,在T=0.08 s时达到第一个峰值,随后迅速下降,T=0.1 s或T=0.12 s达到谷值,持续平缓然后增大,在T=0.15 s时达到最大值,之后持续下降。对比占空比比例1:1,2:1,3:1和4:1的情况,在3:1时,岩屑床运移距离是最大的,故选取占空比比例3:1。
在占空比比例3:1时,脉冲幅度比2.5 %时,岩屑床运移距离未超过常规携岩情况;脉冲幅度比5 %和15 %时,仅在占空比3:1和4:1的情况下岩屑床运移超过了常规携岩;脉冲幅度比7.5 %、10.0 %和12.5 %时,脉冲携岩效果优于常规携岩,尤其在12.5 %时,岩屑床移动距离最大,周期为0.15 s时移动了8.23 m,相比于常规携岩两层水力模型移动距离7.41 m多运移了0.82 m,提升了11.1 %。
通过以上分析,可得出脉冲携岩最佳参数:脉冲周期T=0.15 s,占空比比例b=3:1即占空比为0.75、脉冲幅度比a=12.5 %即脉冲峰值和谷值分为16.875和13.125 L/s。在此参数时,岩屑床移动距离为8.23 m,岩屑床移动速度为0.549 m/s。
3 脉冲携岩与常规携岩对比为对比脉冲携岩与常规携岩的运移规律,以钻杆偏心度为0.16的工况为研究对象,钻井液循环介质为水基泥浆,初始浓度设置为3 %,黏度设置采用幂律模式[10-12]。采用Fluent 15.0软件中Eulerian多项流模型求解钻井液-岩屑两相流[13-17],以此来研究岩屑运移情况。
在研究岩屑运移情况时,应用3个评价指标来评判岩屑的运移情况,该3个评价指标分别为岩屑运移速度、岩屑浓度和岩屑床高度比。在研究对岩屑运移的影响时采用岩屑运移速度和岩屑体积分数来评价。
在距离入口5.000 m处建立了切面plane1,离入口9.000 m处(接头迎风坡面)建立了切面plane2,离入口9.286 m处(接头中心)建立切面plane3,离入口9.526 m处(接头背风坡面)建立了切面plane4,离入口14.526 m出建立了切面plane5。
为详细说明水平井环空岩屑运移的情况,在环空选取5个位置进行了局部放大,图 7和图 8所示为常规携岩和脉冲携岩不同位置处岩屑体积分数。
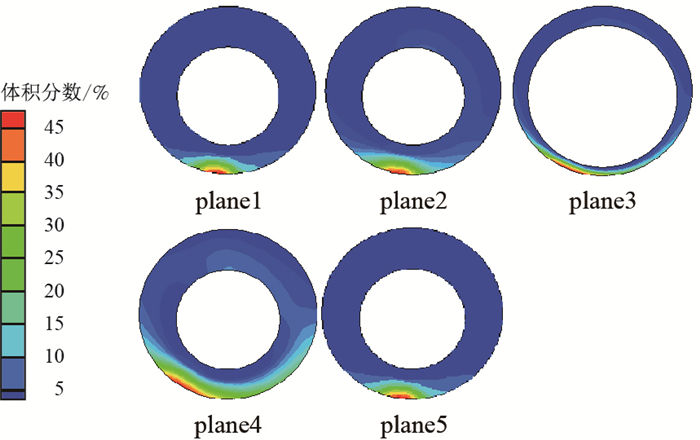 |
| 图7 常规携岩各切片面岩屑体积分数 Fig. 7 Volume fraction of each slice plane in conventional carrying rock cuttings |
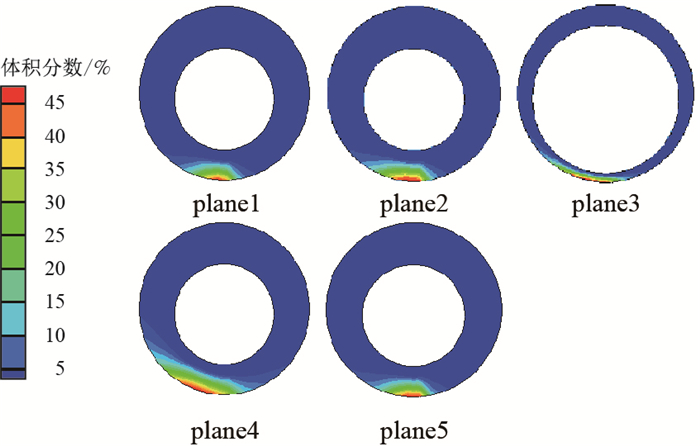 |
| 图8 脉冲携岩各切片面岩屑体积分数 Fig. 8 Volume fraction of each slice plane in pulse carrying rock cuttings |
从图 7和图 8中可观察到,plane1、plane2和plane5处在相同的工况下,采用脉冲携岩方法的环空岩屑体积分数及岩屑床厚度明显小于采用常规携岩方法的环空岩屑体积分数及岩屑床厚度。
图 9和图 10所示为常规携岩和脉冲携岩不同位置处岩屑运移速度。随着到入口距离的增加,常规和脉冲的岩屑运移速度均先增大后减小,在接头中心处最大,环空位置最小,而常规和脉冲的岩屑体积分数都先减小后增大,在背风坡面的岩屑体积分数最小,造成该现象的主要原因是钻柱偏心的存在,环空从而形成了宽流道与窄流道,随着窄流道的横截面积减小,再有岩屑的存在,阻碍了钻井液的流动,所以窄流道的流速较宽流道的流速小,但在接头处,流道横截面积急剧减小,所以岩屑移动速度在接头位置最大,而岩屑体积分数最小。
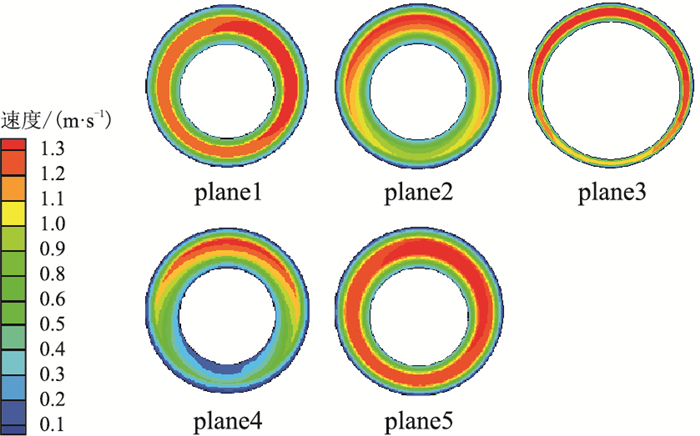 |
| 图9 常规携岩各切片面岩屑运移速度 Fig. 9 Movement speed of each slice plane in conventional carrying rock cuttings |
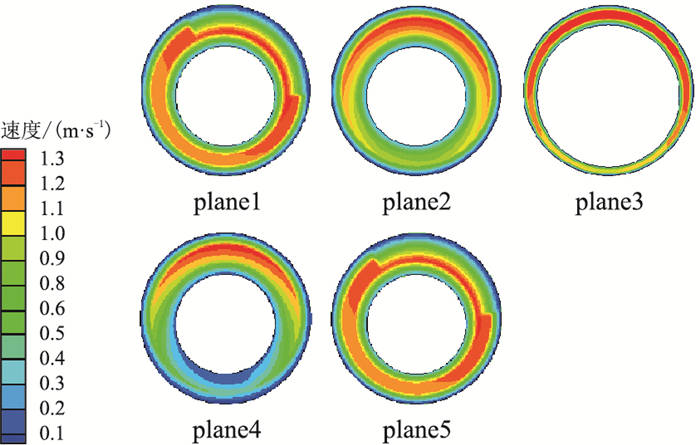 |
| 图10 脉冲携岩各切片面岩屑运移速度 Fig. 10 Movement speed of each slice plane in pulse carrying rock cuttings |
图 11为常规携岩和脉冲携岩仿真结果对比图。
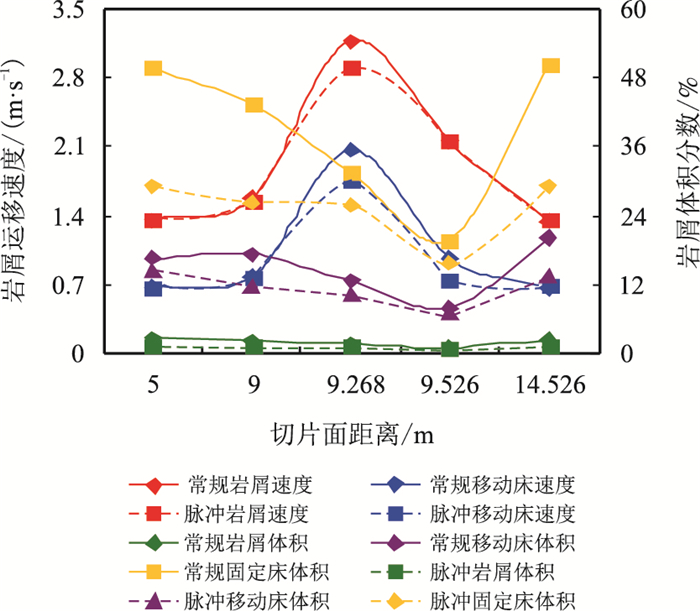 |
| 图11 常规携岩和脉冲携岩仿真结果对比 Fig. 11 Results comparison of conventional carrying rock cuttings and pulse carrying rock cuttings |
从图 11可见,采用脉冲携岩的方法:相对于常规携岩,在plane1和plane5上即环空流场中心处,固定岩屑床体积分数降低了约42 %;接头位置处,固定岩屑床体积分数降低约20 %;另外,移动岩屑床和悬浮岩屑体积分数都有不同程度的减少。
4 脉冲携岩下工况参数对岩屑运移规律的影响分析 4.1 偏心度的影响研究了脉冲携岩下不同偏心度对岩屑运移及岩屑床颗粒分布的影响规律,计算结果如图 12所示。由前面分析可知,钻柱偏心是引起流场大环空和小环空差异的主要原因。随着偏心度的不断增加, 岩屑床的体积分数不断增长,在完全偏心的情况下,固定岩屑床最大体积分数达到了53.2 %,移动岩屑床的体积分数则为30 %。可见,偏心度的增大不利于岩屑清理。
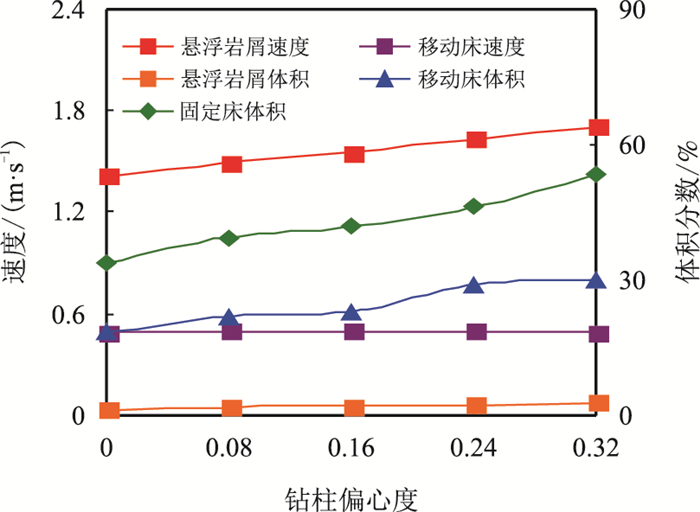 |
| 图12 钻柱偏心对岩屑运移的影响 Fig. 12 Effect of drill pipe eccentricity on cuttings transport |
脉冲携岩下转速0~180 r/min对岩屑运移及岩屑床颗粒分布的影响规律,计算结果如图 13所示。
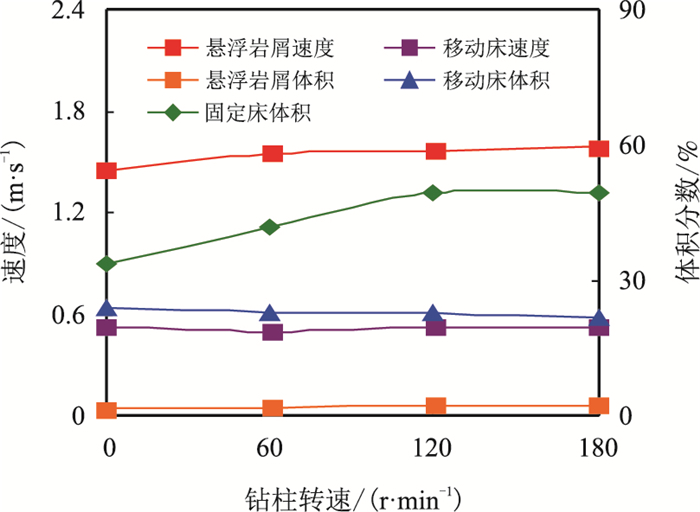 |
| 图13 钻柱转速对岩屑运移的影响 Fig. 13 Effect of drill pipe rotating speed on cuttings transport |
由图 13可见,随着转速的增大,悬浮岩屑运移速度和移动岩屑床速度、悬浮岩屑体积分数、移动岩屑床体积分数变化很小,仅固定岩屑床体积分数逐渐增大,在120 r/min之后趋于平稳。这是由于钻杆旋转对于环空影响区域较小,钻杆旋转产生更多紊流,改变了钻井液径向速度,引起岩屑颗粒径向运移速度的变化,增大了岩屑床里岩屑颗粒的速度,使其达到岩屑临界启动速度,从而减小岩屑床体积分数,达到了破坏岩屑床的目的。在180 r/min时,固定岩屑床和移动岩屑床最大体积分数分别为49.6 %、21.8 %。
4.3 岩屑粒径的影响计算得到脉冲携岩下岩屑粒径为1~5 mm时对岩屑运移及岩屑床颗粒分布的影响规律,如图 14所示。
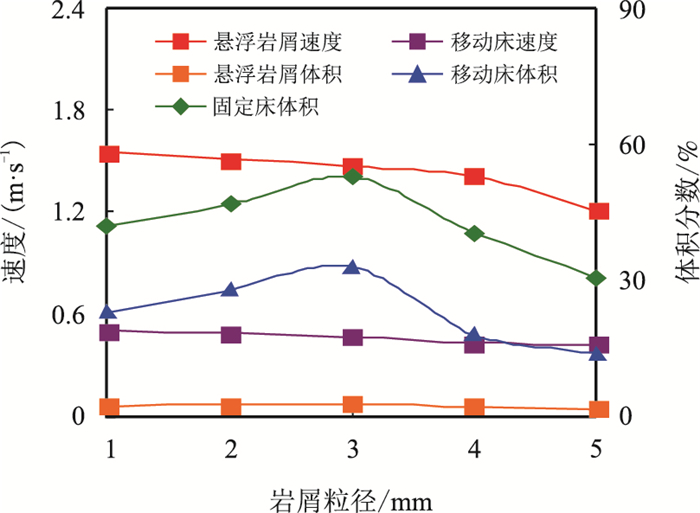 |
| 图14 岩屑粒径对岩屑运移的影响 Fig. 14 Effect of particle size on cuttings transport |
由图 14可见,随着岩屑粒径增大,悬浮岩屑运移速度呈下降趋势,在5 mm岩屑颗粒条件下,悬浮岩屑运移速度及固定岩屑床体积分数分别降低至0.89 m/s和30.6 %。移动岩屑床速度和悬浮岩屑体积分数基本保持不变。随着岩屑颗粒粒径的增大,单颗岩屑体积也在增大,由于密度没有变化,那么单颗岩屑的质量在增加,岩屑由静止状态启动所需能量随之增大,即是临界启动速度在增大,从而导致悬浮岩屑速度和移动床速度降低。
图 15分别为粒径1和5 mm时岩屑体积分数切片图。对比图 15a和图 15b可见,粒径5 mm时,环空下部岩屑床高度增加,堆满了下环空。随着岩屑粒径的增大,单位体积内岩屑所占比重先逐渐饱和然后下降,这就导致了移动岩屑床体积分数先增大后减小。
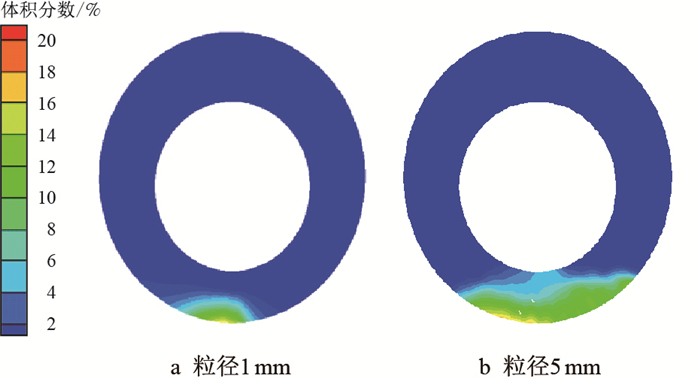 |
| 图15 不同粒径下岩屑体积分数切片图 Fig. 15 Fraction slices of different particle volume with different particle sizes |
研究了脉冲携岩下机械钻速3~15 m/h对岩屑运移及岩屑床颗粒分布的影响规律,计算结果如图 16所示。由图可知,随着入口岩屑浓度的提升,移动岩屑床体积分数和固定岩屑床体积分数不断增加,其中固定床体积分数开始平稳,在机械钻速4.5 m/h时达到31 %之后趋于平缓;而岩屑运移速度并未太大变化。在机械钻速9 m/h时,固定岩屑床和移动岩屑床浓度分别达到了41.8 %、23.0 %。这表明通过调节机械钻速控制岩屑浓度非常有必要,推荐机械钻速范围为4~6 m/h,避免岩屑床浓度过大不易清洗,引起流场不畅通、卡钻等事故。
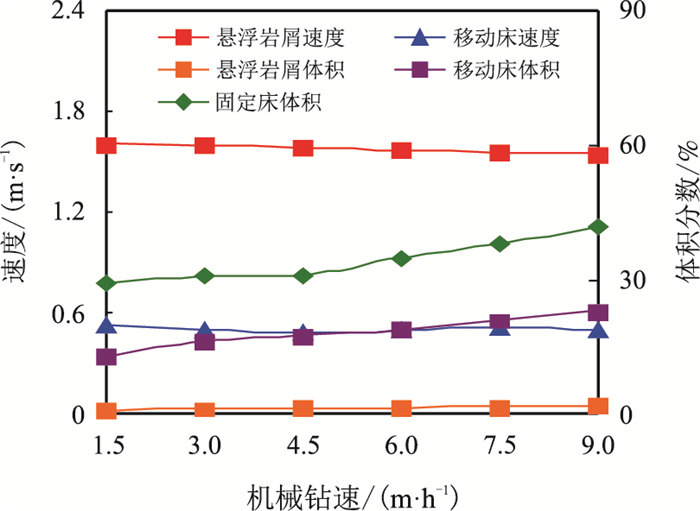 |
| 图16 机械钻速对岩屑运移的影响 Fig. 16 Effect of ROP on cuttings transport |
(1)采用脉冲携岩方法携岩效率要高于常规携岩。脉冲携岩最佳参数:脉冲周期T=0.15 s,占空比为0.75、脉冲峰值和谷值分为16.875 L/s和13.175 L/s。
(2)相对于常规携岩,脉冲携岩在环空流场中心处,固定岩屑床体积分数降低了约42 %;接头位置处,固定岩屑床体积分数降低约20 %;另外,移动岩屑床和悬浮岩屑体积分数都有不同程度的减少。
(3)脉冲携岩下,转速的提升有利于破坏岩屑床,但大于120 r/min后趋于平稳;岩屑粒径大于3 mm时会增加岩屑床高度,不利于清洗井眼,采用低钻速牙轮钻进,即可控制岩屑浓度,也可控制岩屑粒径大小;在危险井段,综合考虑井壁垮塌、岩屑运移不畅和卡钻等因素,推荐机械钻速范围为4~6 m/h。
| [1] |
祝效华, 刘少胡. 气体钻井防沉屑工具分流继能机理与可行性研究[J].
石油钻探技术, 2009, 37(6): 78–80.
ZHU Xiaohua, LIU Shaohu. Working mechanism and application of cutting suspension tool in air drilling wells[J]. Petroleum Drilling Techniques, 2009, 37(6): 78–80. DOI:10.3969/j.issn.1001-0890.2009.06.018 |
| [2] |
祝效华, 贾彦杰, 童华. 气体钻井防沉屑工具结构安全性分析[J].
石油机械, 2009, 37(2): 9–11.
ZHU Xiaohua, JIA Yanjie, TONG Hua. Structure security analysis of cuttings falling-prevention tool for gas drilling[J]. China Petroleum Machinery, 2009, 37(2): 9–11. |
| [3] |
祝效华, 刘少胡, 童华. 结构参数对气体钻井防沉屑工具性能的影响[J].
中国石油大学学报(自然科学版), 2010, 34(6): 56–59.
ZHU Xiaohua, LIU Shaohu, TONG Hua. Influence of structural parameter on performance of cuttings fallingprevent tool in gas drilling[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(6): 56–59. DOI:10.3969/j.issn.1673-5005.2010.06.010 |
| [4] | JOHNSON Jr V E, CHAHINE G L, LINDENMUTH W T, et al. The development of structured cavitating jets for deep-hole bits[C]. SPE 11060, 1982. doi:10.2118/11060-MS |
| [5] |
李根生, 沈忠厚, 周长山, 等. 自振空化射流研究与应用进展[J].
中国工程科学, 2005, 7(1): 27–32.
LI Gensheng, SHEN Zhonghou, ZHOU Changshan, et al. Advances in investigation and application of selfresonating cavitating water jet[J]. Engineering Science, 2005, 7(1): 27–32. DOI:10.3969/j.issn.1009-1742.2005.01.005 |
| [6] |
杨永印, 吴志坚, 沈忠厚, 等. 低压脉冲射流的调制机理及调制器振动模拟[J].
石油大学学报(自然科学版), 2003, 27(3): 40–42.
YANG Yongyin, WU Zhijian, SHEN Zhonghou, et al. Modulation mechanism of low-pressure pulse jet and modulator working simulation[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 2003, 27(3): 40–42. DOI:10.3321/j.issn:1000-5870.2003.03.012 |
| [7] |
李文飞, 杨永印, 夏文安, 等. 自振阀式低压脉冲射流调制器振动特性仿真研究[J].
中国石油大学学报(自然科学版), 2007, 31(3): 59–62.
LI Wenfei, YANG Yongyin, XIA Wen' an, et al. Simulation study on vibration characteristics of Low-pressure pulses jet modulator with Self-vibration valves[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007, 31(3): 59–62. DOI:10.3321/j.issn:1000-5870.2007.03.012 |
| [8] |
雷鹏, 倪红坚, 王瑞和, 等. 自激振荡式旋转冲击钻井工具水力元件性能分析与优化[J].
振动与冲击, 2014, 33(19): 175–180, 198.
LEI Peng, NI Hongjian, WANG Ruihe, et al. Performance analysis and Optimization for hydraulic components of self-oscillating rotary impact drilling tool[J]. Journal of Vibration and Shock, 2014, 33(19): 175–180, 198. DOI:10.13465/j.cnki.jvs.2014.19.030 |
| [9] | 孙余凯, 韦雪洁. 电工电子技术[M]. 北京: 人民邮电出版社, 2010. |
| [10] |
贺成才. 幂律流体在偏心环空中流动的数值模拟[J].
石油学报, 2002, 23(6): 85–89.
HE Chengcai. Numerical simulation of power-law flow in eccentric annulus[J]. Acta Petrolei Sinica, 2002, 23(6): 85–89. DOI:10.3321/j.issn:0253-2697.2002.06.019 |
| [11] | HECKER M T, BARRY M D, MARTIN Jr T B. Reducing well cost by gravel packing in nonaqueous fluid[C]//SPE annual technical conference and exhibition. Houston, Texas:Society of Petroleum Engineers, 2004. doi:10.2118/90758-MS |
| [12] | ZHU X H, SUN C, TONG H. Distribution features, transport mechanism and destruction of cuttings bed in horizontal well[J]. Journal of Hydrodynamics, Ser. B, 2013, 25(4): 628–638. DOI:10.1016/S1001-6058(11)60405-9 |
| [13] | 江帆, 黄鹏. Fluent高级应用与实例分析[M]. 北京: 清华大学出版社, 2008. |
| [14] |
于勇, 张俊明, 姜连田.
Fluent入门与进阶教程[M]. 北京: 北京理工大学出版社, 2008.
YU Yong, ZHANG Junming, et al. Fluent introductory and advanced tutorial[M]. Beijing: Beijing University Of Science And Technology Press, 2008. |
| [15] |
朱红钧, 林元华, 谢龙汉.
FLUENT流体分析及仿真实用教程[M]. 北京: 人民邮电出版社, 2010.
ZHU Hongjun, LIN Yuanhua, et al. FLUENT fluid analysis and the simulation of practical tutorial[M]. Beijing: People'S Posts and Telecommunications Publishing House, 2010. |
| [16] |
吴仲华, 孙浩玉, 聂云飞, 等. 岩屑床破坏工具流场的数值模拟[J].
石油钻探技术, 2007, 9(5): 83–85.
WU Zhonghua, SUN Haoyu, NIE Yunfei, et al. Cuttings bed damage tool flow field numerical simulation[J]. Petroleum Drilling Techniques, 2007, 9(5): 83–85. DOI:10.3969/j.issn.1001-0890.2007.05.024 |
| [17] |
陈锋, 狄勤丰, 袁鹏斌, 等. 高效岩屑床清除钻杆作用机理[J].
石油学报, 2012, 33(2): 298–303.
CHEN Feng, DI Qinfeng, YUAN Pengbin, et al. Mechanism of an effective hydroclean drill pipe for hole cleaning[J]. Acta Petrolei Sinica, 2012, 33(2): 298–303. DOI:10.7623/syxb201202018 |
 2016, Vol. 38
2016, Vol. 38


