2. 西华大学流体及动力机械教育部重点实验室, 四川 成都 600300;
3. 四川省特种设备检验研究院, 四川 成都 610061
2. MOE Key Laboratory of Fluid and Power Machinery, Xihua University, Chengdu, Sichuan 600300, China;
3. Sichuan Special Eqiupment Inspection Institute, Chengdu, Sichuan 610061, China
浮式钻井平台在深水油气开发过程中,由于受到海洋环境中波、浪、流的作用,会产生升沉、纵荡、横荡、平摇、横摇和纵摇6个自由度的复杂空间运动,其中平台升沉运动对钻井作业影响最大,会降低钻井效率和安全性[1]。目前,需要增设升沉补偿装置以解决深水钻井平台的升沉运动补偿问题,保持井底钻压的稳定和提高钻井效率[2-3]。天车升沉补偿装置作为现场使用最为广泛,技术可靠度高的一类升沉补偿装置,主要采用液压驱动方式作为推到浮动天车运动的主要补偿动力源[4-5],见图 1。
 |
| 图1 液压驱动式天车升沉补偿装置 Fig. 1 Hydraulic driven crown-block heave compensation device |
采用液压驱动浮动天车对平台升沉运动进行补偿时,由于液压系统自身存在反应速度较慢,使补偿过程存在较大的滞后性,导致升沉补偿精度不高。采用齿轮齿条机构的机械驱动形式来实现天车升沉补偿装置中浮动天车的补偿运动,该驱动形式具有反应迅速,机构技术可靠性高和能有效提高补偿精度的特点。齿轮齿条驱动机构在海洋装备中已早有成功的应用实例,如自升式钻井平台的升降系统[6-7]等,该机构在煤层气钻机设计和机械传动等具有往复运动过程的领域[8-10]也得到了成熟应用。
利用齿轮齿条这一高可靠性的传动机构,配合驱动电机组成新型机械驱动式的天车升沉补偿装置,对该装置的工作原理和驱动过程进行分析,为该新型天车补偿装置的实用性和可靠性研究奠定基础。
1 补偿装置工作原理新型天车升沉补偿装置的机械驱动结构,如图 2所示。该驱动结构主要由驱动电机、直齿条轨道、主动齿轮和从动齿轮组成,滑块和燕尾滑道用于保持浮动天车运动过程中的受力平衡。选用齿轮齿条机构作为天车升沉补偿装置中浮动天车在既定直线轨道的机械驱动形式,是因该机构具有可靠耐用、维护方便和补偿灵敏度高的特点。
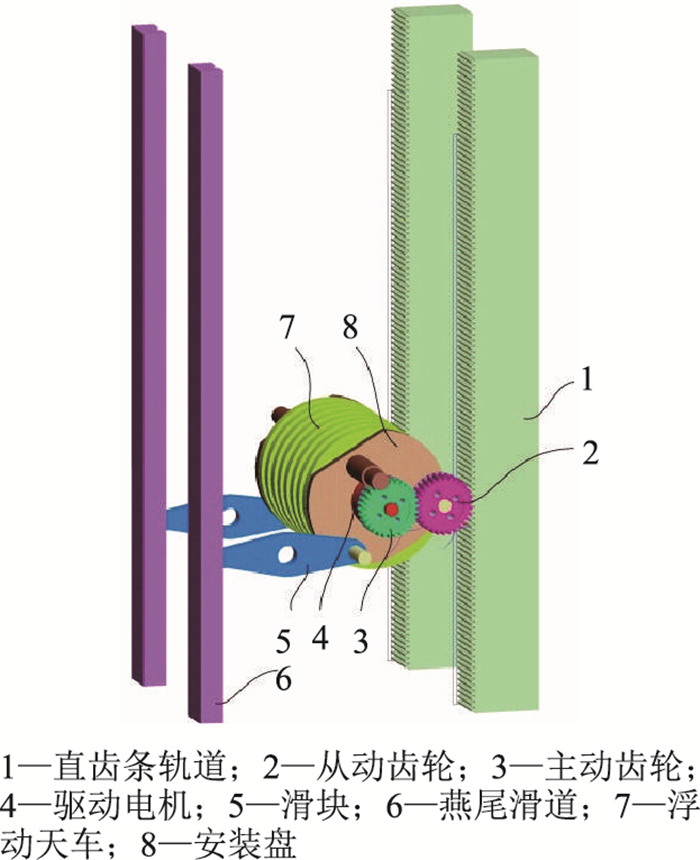 |
| 图2 机械驱动式天车升沉补偿装置三维图 Fig. 2 The three-dimensional figure of mechanical driven crown-block heave compensation device |
齿轮齿条机构[11]作为天车升沉补偿装置机械驱动的关键机构,由外置浮式钻井平台姿态监测系统获得平台升沉运动实时数据,通过控制系统计算出天车升沉补偿量,再启动驱动电机带动主动齿轮运动,从动齿轮由主动齿轮驱动并在直齿条轨道上运动,牵引浮动天车及其所悬挂钻柱在既定直齿条轨道上做补偿运动,用于对浮式钻井平台升沉运动的补偿,保证井底钻压的稳定和提高钻井效率。为保证浮动天车的受力均衡,避免浮动天车在运动过程中的摆动对齿轮和齿条结构轮齿的冲击,使用由两条燕尾滑道和滑块组成滑块滑道机构作为平衡稳定机构。齿轮齿条的选用标准由钻井平台工作海域的海况条件以及钻井工况特点进行组合选配确定。该机械驱动机构被设计成可拆卸式,便于提高天车升沉补偿装置的维护性和运行可靠性。
2 机械驱动装置传动分析 2.1 主动齿轮与从动齿轮传动计算如图 3所示的齿轮齿条机械驱动机构,由于齿条安装在浮动天车所在的钻井井架顶部,采用由主动齿轮从动齿轮组合进行相互啮合的方式对驱动电机驱动补偿能量的传递,避免采用单传动齿轮形式造成的装置运动干扰和难以合理布局的问题。
 |
| 图3 齿轮齿条机械驱动机构 Fig. 3 Mechanical driving mechanism of gear and rack |
直齿条轨道固定在浮动天车平台主框架的支撑板上,主动齿轮和从动齿轮通过安装盘安装在浮动天车两侧,并与直齿条轨道实现啮合传动。由于机械驱动浮动天车对钻柱升沉运动进行补偿的位移较小,一般在10 m振幅范围内进行正弦波动[12]。天车升沉补偿装置进行补偿运动的速度在不大于10 m/s的速度范围内,故齿轮齿条运行速度不高,属于中速重载类型的齿轮传动,根据齿轮传动精度等级的选择和相关应用规范[13],齿轮传动精度选用7级精度。依据常用齿轮材料及其力学性能的相关规范[13],结合齿轮驱动过程中对齿轮接触疲劳极限和弯曲疲劳极限的要求,齿轮材料选用40 Gr(调质),硬度为280 HBS,属于软齿面齿轮。
该机械驱动式齿轮齿条机构属于开式传动,按齿轮传动的轮齿抗弯强度确定主动齿轮模数m,在考虑磨损的条件下,将模数增加20%后进行计算[14],主动齿轮模数m的计算式为
| $ m \geqslant 12.6\sqrt[3]{{\dfrac{{K{T_1}}}{{{\phi _{\rm{m}}}{z_1}}} \cdot \dfrac{{{Y_{{\rm{FS}}}}}}{{[{\sigma _{{\rm{FP}}}}]}}}} $ | (1) |
式中:m——齿轮模数,mm;
K——载荷系数,无因次;文中根据齿轮运转和升沉补偿工况取值1.8;
T1——主动齿轮的转矩,N·m;
z1——从动齿轮齿数;
ϕm——齿宽系数,无因次,文中取1.1;
YFS——复合齿形系数,无因次;
[σFP]——许用弯曲应力,MPa。
对于齿轮接触疲劳强度的计算,由于齿面点蚀破坏发生后会引起齿轮传动噪声和振动增大,不利于保持天车升沉补偿精度和补偿过程的稳定,但不会立即导致齿轮传动停止工作,属于失效概率为1%的一般可靠度齿轮传动,故安全系数可取S=SH=1,SF=1.25,由于天车升沉补偿装置的机械驱动机构属于重载、低速开式齿轮齿条传动,许用接触应力取闭式齿轮齿条传动的1.07倍,则齿轮的许用疲劳强度极限[σH]cl和齿根弯曲疲劳许用应力[σF]cl为
| $ {\left[{{\sigma _{\rm{H}}}} \right]_{\rm cl}} = \dfrac{{1.07{K_{{\rm{HN}}}}{\sigma _{\rm{H}}}_{\lim }}}{S} $ | (2) |
| $ {\left[{{\sigma _{\rm{F}}}} \right]_{\rm cl}} = \dfrac{{{K_{{\rm{FN}}}}{\sigma _{{\rm{FE}}}}}}{S} $ | (3) |
式中:[σH]cl——许用疲劳强度极限,MPa;
[σF]cl——齿根弯曲疲劳许用应力,MPa;
σH lim——接触疲劳极限,MPa,文中依据齿轮的材料和硬度取600 MPa;
S——安全系数,无因次;
KHN——接触疲劳寿命系数,计算取0.97;
KFN——弯曲疲劳寿命系数,计算取0.93;
σFE——弯曲疲劳强度极限,取值500 MPa。
主动齿轮和从动齿轮按照标准中心距a进行安装,啮合点为A,模数为m,齿数分别为z1和z2,如图 4所示,两齿轮间相互接触面的总压力为沿啮合线N1——N2方向的法向力Fn,主动齿轮的转矩为T1,并由天车升沉补偿装置的驱动电机提供,从动齿轮在直齿条轨道上转动的驱动力矩为T2,α为齿轮传动的啮合角。主动齿轮从动齿轮在啮合过程中,法向力Fn可分解为与主动齿轮转动方向相反的圆周力Ft和指向主动齿轮轴心的径向力Fr。
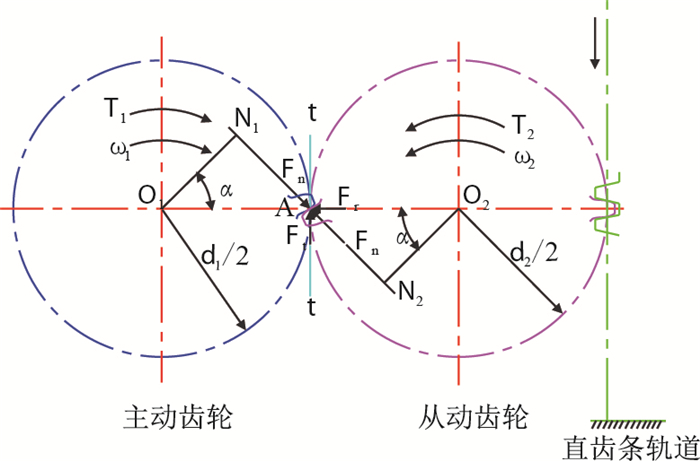 |
| 图4 主动齿轮——从动齿轮驱动机构分析模型 Fig. 4 Driving mechanism analysis model of driving gear-driven gear |
主动齿轮和从动齿轮中心距为
| $ a = \dfrac{m}{2}({z_1} + {z_2}) $ | (4) |
式中:a——中心距,mm;
z2——从动齿轮齿数。
主动齿轮的转矩计算公式为
| $ {T_1} = \dfrac{{{{10}^6}P}}{{{\omega _1}}} = \dfrac{{9.55 \times {{10}^6}P}}{{{n_1}}} $ | (5) |
式中:ω1——主动齿轮角速度,rad/s;
P——主动齿轮传递功率,kW;
n1——主动齿轮转速,r/min。
圆周力计算公式为
| $ {F_{\rm{t}}} = \dfrac{{2{T_1}}}{{{d_1}}} = \frac{{2{T_1}}}{{m{z_1}}} = \frac{{1.91 \times {{10}^7}P}}{{m{z_1}{n_1}}} $ | (6) |
式中:Ft——圆周力,N;
d1——主动齿轮直径,mm。
轴心的径向力计算公式为
| $ \begin{array}{c} {F_{\rm{r}}} = {F_{\rm{t}}}\tan \alpha = \dfrac{{2\tan \alpha {T_1}}}{{m{z_1}}} \\[8pt]{\kern 40pt} = \dfrac{{1.91 \times {{10}^7}\tan \alpha P}}{{m{z_1}{n_1}}} \end{array} $ | (7) |
式中:Fr——径向力,N;
α——啮合角,rad。
法向力计算公式为
| $ \begin{array}{c} {F_{\rm{n}}} = \dfrac{{{F_{\rm{t}}}}}{{\cos \alpha }} = \dfrac{{2{T_1}}}{{m{z_1}\cos \alpha }} = \dfrac{{1.91 \times {{10}^7}P}}{{m{z_1}{n_1}\cos \alpha }} \end{array} $ | (8) |
式中:Fn——法向力,N。
从动齿轮的转矩计算公式为
| $ {T_2} = \dfrac{{{F_{\rm t}}{d_2}}}{2} = \dfrac{{9.55 \times {{10}^6}{z_2}P}}{{{z_1}{n_1}}} $ | (9) |
式中:T2——从动齿轮的转矩,N·m;
d2——从动齿轮直径,mm。
2.2 从动齿轮与直齿条轨道的传动计算由图 4知,从动齿轮将驱动电机的驱动力由主动齿轮传递到直齿条轨道,由于直齿条轨道底端固定在钻井井架上,从动齿轮作为动齿轮带动浮动天车在直齿条轨道上运动。运动啮合过程中,由于直齿条轨道处于静止固定状态,在驱动电机和主动齿轮的带动下,外部力矩的波动使从动齿轮与直齿条轨道在该过程中受到外界振动冲击作用;同时从动齿轮与直齿条轨道也会受到自身刚度、啮合齿廓误差和相互撞击的影响[15-16]。
根据从动齿轮与固定直齿条轨道在啮合过程中的内部激励影响[17-18],建立如图 5所示的啮合振动分析模型(Kv——刚度系数,无因次,刚度数与从动齿轮和直齿条轨道的啮合位置相关,随时间不同而变化;e——齿轮齿条间的齿廓误差系数,无因次;Cv——啮合过程中的阻尼系数,无因次)。对从动齿轮和直齿条轨道进行啮合过程的动力学分析过程如下:
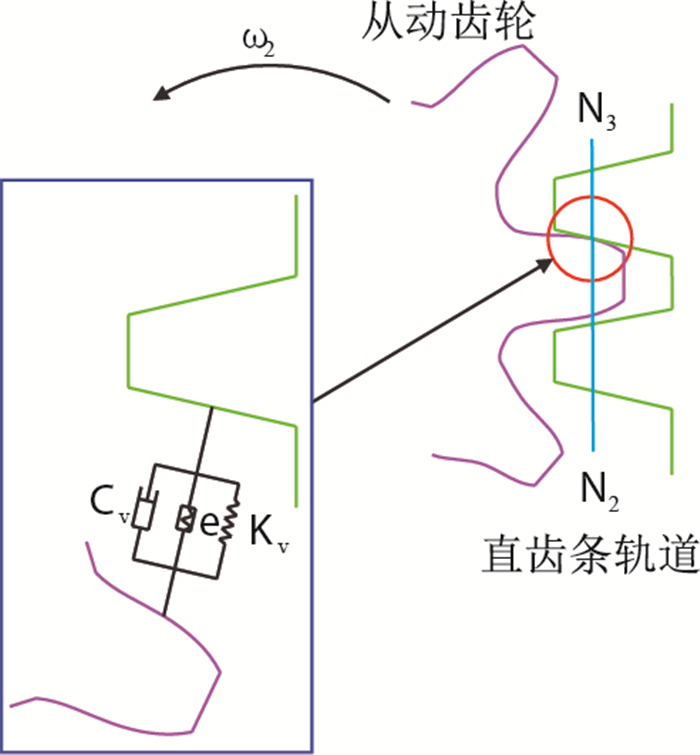 |
| 图5 从动齿轮——直齿条轨道的啮合振动分析模型 Fig. 5 Meshing vibration analysis model of driven gear-straight orbit rack |
设从动齿轮与直齿条轨道的重合度为ε(1 < ε < 2),齿轮齿条在啮合过程中的啮合齿对为n(n=1,2),则啮合齿对在啮合线N2-N3上的变形量为:
| $ {\zeta _n} = \dfrac{{{d_{\rm{b}}}}}{2}\beta-s-({e_n}_1 + {e_n}_2) $ | (10) |
式中:ζn——啮合齿对n在啮合线上的变形量,mm;
db——从动齿轮基圆直径,mm;
β——从动齿轮转动角度,rad;
s——从动齿轮的下降位移,m;
en1,en1——从动齿轮与直齿条轨道啮合齿对n的齿廓误差,mm。
考虑啮合过程中阻尼系数的情况下[19-20],从动齿轮与直齿条轨道的动态法向啮合力Fnlt为
| $ %\begin{array}{c} {F_{\rm{n}}}_{{\rm{lt}}} = \sum\limits_n {\left [{K_{{\rm{v}}n}}({\zeta _n})+ {C_{{\rm{v}}n}}({{\dot \zeta }_n})\right ]} \\{\kern 40pt} = \sum\limits_n {{K_{{\rm{v}}n}}\left (\dfrac{{{d_{\rm{b}}}}}{2}\beta-s-{e_n}_1-{e_n}_2 \right)+ } \\ {\kern 40pt} \sum\limits_n {C_{{{\rm v}}n}}\left (\dfrac{{{d_{\rm{b}}}}}{2}\dot \beta-\dot s-{{\dot e}_{n1}}-{{\dot e}_{n2}}\right) %\end{array} $ | (11) |
式中:Fnlt——啮合力,N;
Kvn——齿对n的刚度系数,无因次;
Cvn——齿对n的阻尼系数,无因次;
对于齿轮齿条啮合过程中的刚度系数,可由式(12)进行计算
| $ \left\{ \begin{array}{l} {K_{{\rm v}n}} = \dfrac{4}{3}E\sqrt R \\[5pt] \dfrac{1}{E} = \dfrac{{1-{\gamma _1}^2}}{{{E_1}}} + \dfrac{{1-{\gamma _2}^2}}{{{E_2}}}\\[5pt] \dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \end{array} \right. $ | (12) |
式中:E1、E2——齿轮齿条的弹性模量,MPa;
R1、R2——齿轮齿条啮合时接触点半径,m;
γ1、γ2——齿轮齿条的泊松比,无因次。
啮合过程中的阻尼系数取刚度系数的0.1%~1.0%[21]。
啮合过程中,设从动齿轮的质量和转动惯量分别为M和J,并在直齿条轨道上受到的阻力为FR,与齿轮运动方向相反,则从动齿轮与直齿条轨道在啮合运动过程中的力矩平衡方程为
| $ \left\{ \begin{array}{l} M\ddot s = {F_{\rm{n}}}_{{\rm{lt}}}\cos \alpha-{F_{\rm{R}}}\\ J\ddot \beta = {T_2}-\dfrac{{{d_{\rm{b}}}}}{2}{F_{\rm{n}}}_{{\rm{lt}}} \end{array} \right. $ | (13) |
式中:M——从动齿轮的质量,kg;
FR——阻力,N;
J——从动齿轮的转动惯量,kg·m2;
对于标准齿轮,啮合角α=20°,将式(10)和式(11)代入式(13)中,得到
| $ \left\{ \begin{array}{l} {F_{\rm{R}}} = \sum\limits_n {{K_{{\rm v}n}}\left(\dfrac{{{d_{\rm{b}}}}}{2}\beta-s-{e_n}_1-{e_n}_2\right)} +\\{\kern 15pt} \sum\limits_n{C_{{\rm v}n}}\left(\dfrac{{{d_b}}}{2}\dot \beta-\dot s-{{\dot e}_{n1}}-{{\dot e}_{n2}}\right)\cos \alpha-m\ddot s\\ {T_2} = \sum\limits_n {{K_{{\rm v}n}}\left(\dfrac{{{d_{\rm{b}}}}}{2}\beta-s-{e_n}_1-{e_n}_2\right)} \\{\kern 15pt} + {C_{{\rm v}n}}\left(\dfrac{{{d_{\rm{b}}}}}{2}\dot \beta-\dot s-{{\dot e}_{n1}}-{{\dot e}_{n2}}\right)+ J\ddot \beta \end{array} \right. $ | (14) |
以从动齿轮转速n2=300 r/min、齿数z2=30、模数m=8和直齿条轨道长度取4 m进行数值计算,求得从动齿轮运动量、啮合力与时间的变化关系如图 6~图 8所示。
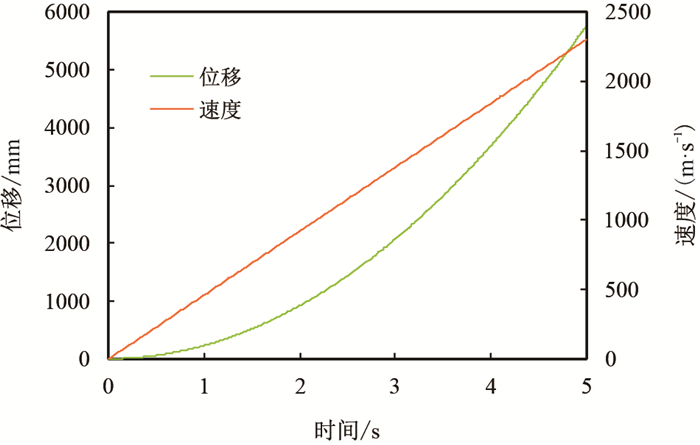 |
| 图6 位移/速度随时间变化曲线 Fig. 6 The curve of displacement and velocity changing with time |
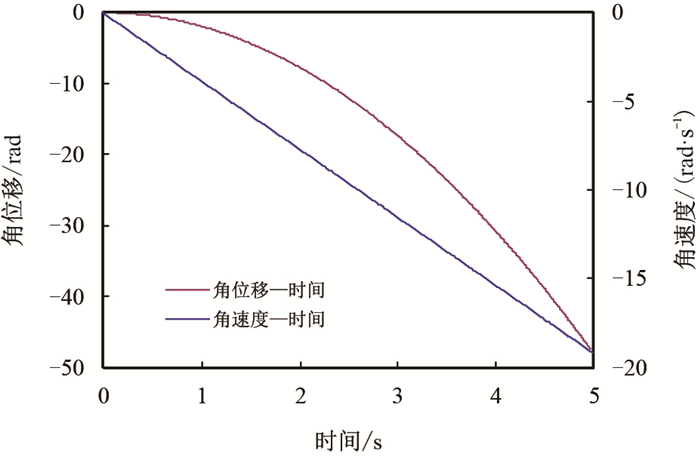 |
| 图7 角位移/角速度随时间变化曲线 Fig. 7 The curve of angular displacement and angular velocity changing with time |
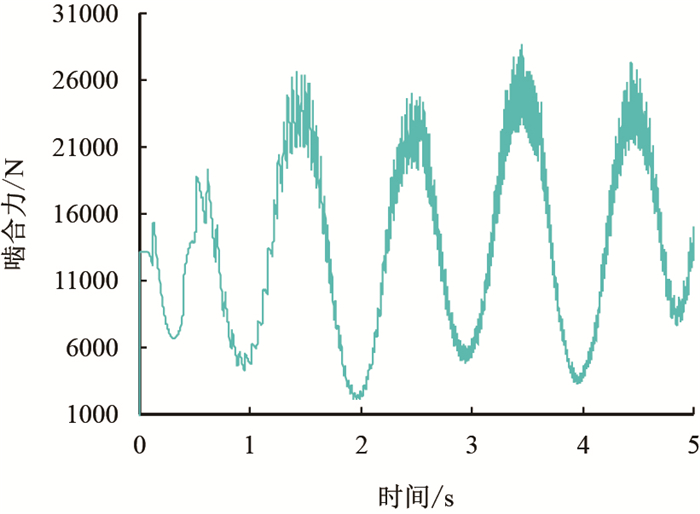 |
| 图8 啮合力随时间变化曲线 Fig. 8 The curve of meshing force changing with time |
由式(14)和图 8可知,即使主动齿轮和从动齿轮转速和传递载荷处于稳定状态,由于从动齿轮和直齿条轨道之间刚度系数随啮合位置不同而产生变化,使从动齿轮在运动过程中产生动态变化的啮合力,会对天车升沉补偿装置的机械驱动机构产生一定的振动激励影响,需要在浮动天车机械驱动装置的一端增设有助于平稳运动的滑块滑道运动机构。
3 结语天车升沉补偿装置作为现有一类技术可靠,应用广泛的海洋石油装备,一般采用液压驱动方式使补偿过程具有反应滞后性较大,补偿精度不高的特点。新提出的机械驱动式天车升沉补偿装置,以主动齿轮—从动齿轮—直齿条轨道作为驱动力传递机构,以滑块滑道作为载荷平衡机构,在驱动电机的配合下可提高天车升沉补偿精度和效率。
在对机械驱动式天车升沉补偿装置工作原理的分析基础上,提出机械驱动式补偿装置的具体结构,并对主动齿轮与从动齿轮的安装、选材和设计验算进行分析,同时还得到两齿轮在传动过程中的载荷分布情况。
对从动齿轮和直齿条轨道的传动分析过程中,采用动力学分析方法建立起齿轮齿条啮合过程动力振动分析模型,得到啮合过程的力矩平衡方程,发现采用该机械驱动结构会对直齿条轨道产生一定的振动激励。
| [1] |
姜浩, 刘衍聪, 张彦廷, 等. 浮式钻井平台主动式钻柱升沉补偿装置设计[J].
石油学报, 2012, 33(3): 483–486.
JIANG Hao, LIU Yancong, ZHANG Yanting, et al. Design for an active drill-string heave compensation system of the floating drilling platform[J]. Acta Petrolei Sinica, 2012, 33(3): 483–486. DOI:10.7623/syxb201203021 |
| [2] |
刘清友, 徐涛. 深海钻井升沉补偿装置国内现状及发展思路[J].
西南石油大学学报(自然科学版), 2014, 36(3): 1–8.
LIU Qingyou, XU Tao. Domestic status and thoughts on the development ideas of deepwater drilling heave compensation system[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(3): 1–8. DOI:10.11885/j.issn.1674-5086.2013.12.07.01 |
| [3] |
张萌, 李相远, 朱显宇. 主动式钻柱升沉补偿系统模拟实验及仿真[J].
机床与液压, 2014, 42(21): 132–135.
ZHANG Meng, LI Xiangyuan, ZHU Xianyu. Experiment and simulation of active type drill string heave compensation system[J]. Machine Tool & Hydraulics, 2014, 42(21): 132–135. DOI:10.3969/j.issn.1001-3881.2014.21.035 |
| [4] |
张彦廷, 渠迎锋, 刘振东, 等. 天车升沉补偿系统摇摆装置的设计[J].
浙江大学学报(工学版), 2012, 46(12): 2268–2273.
ZHANG Yanting, QU Yingfeng, LIU Zhendong, et al. Design of swing device for crown-block heave compensation system[J]. Journal of Zhejiang University (Engineering Science), 2012, 46(12): 2268–2273. DOI:10.3785/j.issn.1008-973X.2012.12.019 |
| [5] | Castor Drilling Solution (CDS). Crown mounted compensator[EB/OL]. http://www.cds.as/products.htm#+Crown Mounted Compensator. |
| [6] |
蒙占彬, 曹宇光, 张士华. 自升式平台齿轮—齿条升降系统结构设计[J].
机械设计与制造, 2013(11): 33–35.
MENG Zhanbin, CAO Yuguang, ZHANG Shihua. Structural design of the rack and pinion jacking system of jack-up platforms[J]. Machinery Design & Manufacture, 2013(11): 33–35. DOI:10.3969/j.issn.1001-3997.2013.11.010 |
| [7] |
王钢, 孟祥伟, 彭曼, 等. 自升式平台支撑升降系统结构设计与分析[J].
机械设计, 2011, 28(7): 42–46.
WANG Gang, MENG Xiangwei, PENG Man, et al. Design and analysis on fixation and jacking system of jackup platform[J]. Journal of Machine Design, 2011, 28(7): 42–46. |
| [8] |
常玉连, 李军, 任福深, 等. 具有主动加压钻进功能钻机的技术发展[J].
石油机械, 2013, 41(1): 1–5.
CHANG Yulian, LI Jun, REN Fushen, et al. Technological development of the active pressure drilling rig[J]. China Petroleum Machinery, 2013, 41(1): 1–5. DOI:10.3969/j.issn.1001-4578.2013.01.001 |
| [9] | MAZEROV K. Multifunctional rack and pinion technology takes shape in oilfield as versatile, mobile rigs[J]. Drilling Rig Equipment, 2008: 32–39. |
| [10] |
苏艳, 李涛涛, 郭燕. 基于Adams的齿轮—齿条变幅驱动动力学研究[J].
武汉理工大学学报(信息与管理工程版), 2013, 35(6): 856–858.
SU Yan, LI Taotao, GUO Yan. Dynamics study on rack and pinion luffing mechanism based on Adams[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2013, 35(6): 856–858. DOI:10.3963/j.issn.2095-3852.2013.06.016 |
| [11] | 刘清友, 黎伟, 鲁柳利, 等.一种浮式钻井平台齿轮—齿条式钻柱升沉补偿装置:中国, 201210095435. X[P]. 2014-04-09. |
| [12] |
姜浩, 刘衍聪, 张彦廷, 等. 浮式钻井平台被动升沉补偿装置设计[J].
液压与气动, 2011(10): 50–52.
JIANG Hao, LIU Yancong, ZHANG Yanting, et al. Research of passive heave compensation system for float drilling platform[J]. Chinese Hydraulics & Pneumatics, 2011(10): 50–52. DOI:10.3969/j.issn.1000-4858.2011.10.017 |
| [13] | 杨可桢, 程光蕴, 李仲生. 机械设计基础[M]. 北京: 高等教育出版社, 2006. |
| [14] | 阎邦椿. 机械设计手册(第二卷)[M]. 5版. 北京: 机械工业出版社, 2010. |
| [15] |
常乐浩, 刘更, 吴立言, 等. 不同形式齿廓偏差对直齿轮副振动的影响规律[J].
振动与冲击, 2014, 33(19): 22–29.
CHANG Lehao, LIU Geng, WU Liyan, et al. Effects of different tooth profile deviations on vibration of a spur gear pair[J]. Journal of Vibration and Shock, 2014, 33(19): 22–29. DOI:10.13465/j.cnki.jvs.2014.19.004 |
| [16] |
韩静波, 刘更, 吴立言, 等. 齿轮系统动力学误差激励合成方法研究[J].
机械传动, 2009, 33(5): 24–26.
HAN Jingbo, LIU Geng, WU Liyan, et al. Study on method of synthesizing error excitation about gear system dynamics[J]. Journal of Mechanical, 2009, 33(5): 24–26. DOI:10.16578/j.jssn.1004.2539.2009.05.010 |
| [17] |
马宝, 唐文献, 章子玲, 等. 超大模数齿轮的参数化建模及接触分析[J].
机械传动, 2012, 36(4): 44–47.
MA Bao, TANG Wenxian, ZHANG Ziling, et al. Parametric modeling and contact analysis of supper large modlule pinion[J]. Journal of Mechanical Transmission, 2012, 36(4): 44–47. DOI:10.3969/j.issn.1004-2539.2012.04.013 |
| [18] |
曹宇光, 张士华, 刘海超, 等. 大型开式齿轮损伤强度数值模拟分析[J].
中国石油大学学报(自然科学版), 2012, 36(5): 129–135.
CAO Yuguang, ZHANG Shihua, LIU Haichao, et al. Numerical simulation analysis of damages on strength of large-scale open gears[J]. Journal of China University of Petroleum, 2012, 36(5): 129–135. DOI:10.3969/j.issn.1673-5005.2012.05.024 |
| [19] |
曾作钦, 赵学智. 啮合刚度及啮合阻尼对齿轮振动影响的研究[J].
机床与液压, 2010, 38(5): 32–34.
ZENG Zuoqin, ZHAO Xuezhi. Study about the effect of meshing stiffness and meshing damping on gear vibration[J]. Machine Tool & Hydraulics, 2010, 38(5): 32–34. DOI:10.3969/j.issn.1001-3881.2010.05.010 |
| [20] |
赵宁, 郭志强, 付晨曦, 等. 啮合刚度及阻尼对人字齿轮振动特性的影响[J].
机械科学与技术, 2013, 7(13): 1757–1763.
ZHAO Ning, GUO Zhiqiang, FU Chenxi, et al. The effect of meshing stiffness and meshing damping on dynamics characteristic of herringbone gears[J]. Science Technology and Engineering, 2013, 7(13): 1757–1763. DOI:10.3969/j.issn.1671-1815.2013.07.010 |
| [21] | 谢最伟, 吴新跃.基于ADAMS的碰撞仿真分析[C]//第三届中国CAE工程分析技术年会暨2007全国计算机辅助工程(CAE)技术与应用高级研讨会论文集.大连:中国机械工程学会, 2007:339-342. |
 2016, Vol. 38
2016, Vol. 38


