2. 西南石油大学地球科学与技术学院, 四川 成都 610500
2. School of Geoscience and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China
南海地区某气田在勘探过程中钻遇一套厚度较大、孔渗性能较好的气层,但部分井的测试结果显示储层中二氧化碳所占气体总体积的比例达70%以上[1-2]。实验发现,将混有不同百分含量二氧化碳气体的天然气分别与地层水混合,测得不同样本的导电性差异微乎其微且无明显规律性,即二氧化碳溶于水所产生的附加导电性并不明显[3]。因此,常规的以电阻率为主要标志的气层识别方法在识别二氧化碳时并不适用。
考虑到储层处在高温高压条件下,二氧化碳处于一种超临界状态[4-6](即温度和压力均超过其临界值),其密度和声波速度与烃类气体存在一定差异,前人据此提出了一些识别烃类与二氧化碳的方法。郭栋通过分析地震亮点、AVO特征和地表化探异常与二氧化碳气藏的关系,运用地震亮点、AVO、叠后滤波处理、约束反演和地球化学识别技术,有效地识别和预测了二氧化碳气的分布[7-8]。刘中奇等根据二氧化碳气层和烃类气层在声波时差和密度测井响应上的差异,提出了利用声波—密度孔隙度差值法、孔隙度比值重叠法、气饱和度法等多种方法定性识别二氧化碳气体[9]。孟祥水等提出利用视孔隙度差异识别二氧化碳的方法,通过计算中子测井视孔隙度与密度测井视孔隙度之间的差值,将该计算差值与理论值进行对比,来区分地层中气体的组份[10]。上述方法都是以二氧化碳和甲烷在密度和声波时差上的差异为基础的定性识别方法,仍然没有很好地解决定量计算二氧化碳含量的问题。
针对二氧化碳对热中子减速和扩散过程的影响有较大差异这一现象,本文采用中子测井曲线和基于体积模型的最优化方法对地层中二氧化碳含量进行定量计算,并将计算结果与实际试气资料进行了对比,较好地解决了地层中二氧化碳含量的问题。
1 中子长短源距计数率法计算二氧化碳含量 1.1 长短源距计数率的物理意义在研究同位素中子源发射出的中子在地层中的迁移扩散时,一般将中子的运动过程分成几个阶段,不同阶段内中子能量不同,可用不同的扩散方程表示。考虑到井下测量可能达到的精度,在大多数条件下双组扩散理论就可以满足需要,即把中子迁移运动过程分为慢中子减速阶段和热中子扩散阶段两个阶段即可。由于补偿中子测井采用了足够大的源距,故针对中子运动的第二个过程——热中子扩散过程建立扩散方程
| ${D_{\rm{t}}}{\nabla ^2}{\phi _{\rm{t}}}(r) - {\Sigma _{\rm{t}}}{\phi _{\rm{t}}}(r) + {\Sigma _{\rm{f}}}{\phi _{\rm{f}}}(r) = 0$ | (1) |
其解为
| ${\phi _{\rm{t}}}(r) = \frac{1}{{4\pi {D_{\rm{t}}}r}}\frac{{L_{\rm{t}}^2}}{{L_{\rm{f}}^2 - L_{\rm{t}}^2}}({{\rm{e}}^{ - r/{L_{\rm{f}}}}} - {{\rm{e}}^{ - r/{L_{\rm{t}}}}})$ | (2) |
式中: ${\phi _{\rm{f}}}(r)$、${\phi _{\rm{t}}}(r)$—无限均匀介质中第一组(慢中子减速)和第二组(热中子扩散)中子距源r处的通量,cm$^{-2}\cdots^{-1}$;
r—源距,m;
$\Sigma _{\rm{t}}$、$\Sigma _{\rm{f}}$—第一组和第二组中子的宏观组转移截面,cm$^{-1}$;
$D_{\rm{t}}$—热中子扩散系数,无因次;
$L_{\rm{f}}$—慢中子减速长度,m;
$L_{\rm{t}}$—热中子扩散长度,m;
下标:f—慢中子减速阶段,t—热中子扩散阶段。
从式(1)可以看出,单一源距的热中子通量受不同介质的吸收性质及井环境的影响较大。由于快中子减速长度近似为热中子扩散长度的两倍,在源距r较大的条件下,式(1)中的第二项可以忽略。在源距足够长的前提之下,取不同源距的两个计数率作比值,可得
| $R = \dfrac{{\phi ({r_1})}}{{\phi ({r_2})}} = \dfrac{{{r_2}}}{{{r_1}}} {\textrm{e}^{ - ({r_1} - {r_2})/{L_{\rm{f}}}}}$ | (3) |
式中: R—长短源距计数率比值,无因次。
运用这种方法,可以在很大程度上补偿地层吸收和井环境对孔隙度的影响。但对于烃气和二氧化碳气体来说,虽然含氢指数有一定差异,但由于补偿中子长短源距计数率比只体现了长源距和短源距之间范围内中子减速与扩散特征,弱化了含氢指数不同的气体在补偿中子测量值上差异的体现,加之孔隙中束缚水饱和度计算精度等原因,使得相同真实孔隙度条件下不同气体类型储层补偿中子测井值往往十分接近,故需要突出不同类型孔隙流体对中子扩散吸收性质的差异[11]。因此,在井环境相同的条件下,直接建立二氧化碳含量与长短源距计数率的关系,可以使二氧化碳定量计算结果更加准确。
1.2 资料预处理及模型建立由于各井的测井环境不尽相同,故在进行定量解释之前需要对测井资料进行预处理,以达到建立符合整个地区测井解释标准的目的。一般只进行归一化校正即可获得较好的解释精度。以长源距计数率为例,归一化的具体方法如下
| $N_{\rm{LS}}^{'} = \dfrac{N_{\rm{LS}} - N_{\rm{LS,min}}}{N_{\rm{LS,max}} - N_{\rm{LS,min}}}$ | (4) |
式中: $N_{\rm{LS}}^{'}$—长源距计数率归一化值,无因次;
$N_{\rm{LS}}$—当前深度点的长源距计数率值,无因次;
$N_{\rm{LS,\min}}$—全井段长源距计数率最小值,无因次;
$N_{\rm{LS,\max}}$—全井段长源距计数率最大值,无因次。
为实现二氧化碳含量的定量计算,需要建立长短源距计数率值与试油资料中二氧化碳含量之间的统计关系模型。在对原始数据处理和分析的过程中发现,二氧化碳含量随长源距计数率的增大先缓慢增加,再加速上升,最后又缓慢增加,并最终接近于1,即二氧化碳含量与长源距计数率的变化关系符合典型的S型曲线形态。以Logistic曲线(S型曲线的一种)为基本模型,通过系数拟合,得到长源距计数率与二氧化碳含量的关系(图 1)。
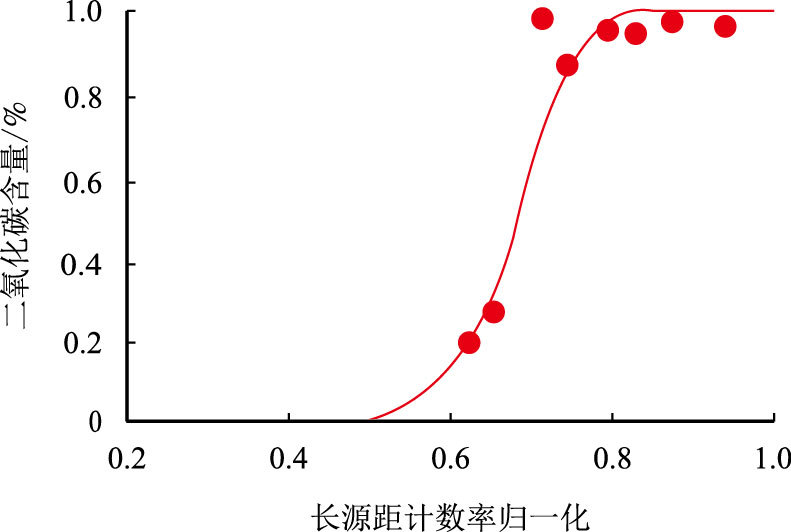 |
| 图1 二氧化碳含量与长源距计数率归一化值的S型曲线形态关系图 Fig. 1 Relationship of S-size curve between CO$_2$ content and the normalized value of long spacing counting rate |
这种关系用方程表示,则为
| ${x_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = \dfrac{1}{{1 + 986.87{\textrm{e}^{ - 25.023({N_{{\rm{LS}}}} - 0.391)}}}}$ | (5) |
式中: ${x_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}$—二氧化碳含量,无因次。
考虑到孔隙度的大小对长短源距计数率存在影响,故也可以用长、短源距计数率和中子测井值与二氧化碳含量建立多项式多元回归关系。当同时选取长源距和短源距计数率作为自变量时,其具体形式如下
| $\begin{array}{l} {x_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = 25.022{N_{{\rm{LS}}}}{\rm{ - }}12.947{N_{{\rm{SS}}}} - 14.478N_{{\rm{LS}}}^2 - \\ 8.351N_{{\rm{SS}}}^2{\rm{ - }}0.029{\rho _{{\rm{CNL}}}} - 4.361 \end{array}$ | (6) |
式中: $\rho _{{\rm{CNL}}}$—中子测井值,%;
$N_{\rm{SS}}$—短源距计数率归一化值,无因次。其相关系数为0.992。
若只选取长源距计数率作为单一源距计数率的自变量,其具体形式可表示为
| ${x_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} = 24.448{N_{{\rm{LS}}}} - 14.376N_{{\rm{LS}}}^2 - 0.0256{\rho _{{\rm{CNL}}}} - 8.999$ | (7) |
其相关系数为0.994。
从式(6)、式(7)可以看出,二氧化碳含量同长短源距计数率值、中子测井值等参数存在良好的函数关系,在实际处理中可以运用上述模型对二氧化碳含量进行计算。
2 最优化方法定量计算二氧化碳含量 2.1 最优化方法原理及可行性通过实验得知,在地下150~℃和50 MPa内压的温压条件下,甲烷气体密度为0.213 g/cm3,纵波时差为395.85 $\mu $s/ft,二氧化碳气体的密度为0.735 g/cm3,纵波时差为545.27 $\mu $s/ft,两者的物理性质不同(如密度、纵波时差等),导致在二氧化碳含量不同的地层,三孔隙度测井响应也会不同[12]。同时,两种气体表现在不同物理性质上的差异程度不同(二氧化碳的纵波速度略小于甲烷,但密度却远大于甲烷),使得将不同的测井响应方程联立求解不同流体成分各自的含量成为可能。在对本地区二氧化碳定量求解中,选用的是基于岩石体积物理模型的最优化算法。
最优化建模的一般模型可表示为
| $\min f(X)(或\max f(X))$ | (8) |
其约束条件为
| $\left\{ \begin{array}{l} {g_i}(X) \geqslant 0\\ {h_j}(X) = 0 \end{array} \right.$ |
式中: $\min$、$\max$—目标函数的最小值和最大值(根据模型具体情况而定);
h、g—约束函数;
$i=$1,2,$\cdots$,m;$j=$1,2,$\cdots$,p。
因此,最优化模型的建立,实际上就是一个从确定决策变量到确定目标函数再到确定约束条件的过程[13-16]。
2.2 最优化模型及约束条件的确定在运用基于岩石体积物理模型的最优化方法时,需要把岩石分为骨架、泥质、地层水、甲烷和二氧化碳共5个部分[17-20]。如果将这5个部分均作为未知数进行定量最优化求解,则可能会出现由于其中几个变量结果误差的累积导致其余几个变量与真实值出现较大偏差。因此在最优化求解中,应尽量避免出现过多的未知变量。考虑到本地区计算孔隙度和饱和度的方法的正确性已经得到验证,故可以将用已知模型计算出来的泥质、骨架以及地层水的相对体积作为已知量,用最优化方法计算出甲烷气体和二氧化碳气体的相对体积[21-23]。在实际处理时发现,运用密度和纵波时差曲线计算孔隙度精度更高且相邻深度点无明显跳变,同时考虑到气体对补偿中子测井的挖掘效应使得气体饱和度的计算不够精确,故运用密度和纵波时差的体积物理模型进行最优化建模(图 2)。
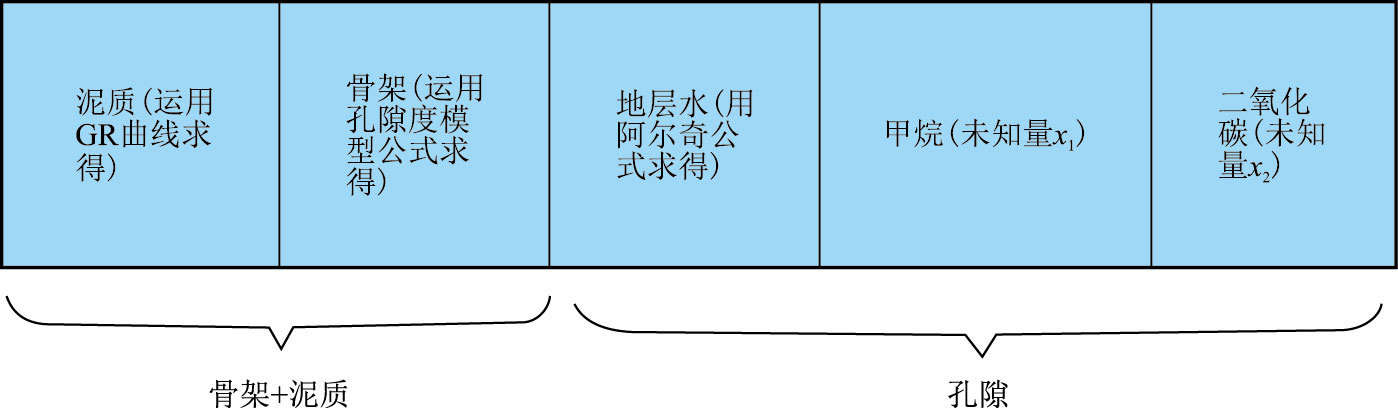 |
| 图2 最优化算法体积物理模型示意图 Fig. 2 Model for physical volume of optimization algorithm |
目标函数与约束条件实际上是为了使体积物理模型计算得到的结果同测井值的差距达到最小,计算得到的值可以通过不同的目标函数和约束条件组合,从不同的方向逼近测井值(两组目标函数分别从最小值和最大值的方向逼近测井值,共4种不同的逼近方向)。按照Matlab多目标最优化程序所要求的目标函数和约束条件格式,以两组目标函数同时从负方向(最大值方向)逼近为例进行说明。
目标函数为
| ${\max}\left ({\rho _{\rm{CO}2}} {V_{\rm{CO}2}} + {\rho _{\rm{CH}4}} {V_{\rm{CH}4}}\right)$ | (9) |
| $\max \left( {\Delta {t_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} + \Delta {t_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{V_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}}} \right)$ | (10) |
约束条件为
| ${\rho _{{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{V_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}} + {\rho _{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} \leqslant \rho - {\rho _{\rm{w}}}{V_{\rm{w}}} - {\rho _{{\rm{sh}}}}{V_{{\rm{sh}}}} - {\rho _{{\rm{ma}}}}{V_{{\rm{ma}}}}$ | (11) |
| $\Delta {t_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}}{V_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}} + \Delta {t_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} \leqslant \Delta t - \Delta {t_{\rm{w}}}{V_{\rm{w}}} -\Delta {t_{{\rm{ma}}}}{V_{{\rm{ma}}}} - \Delta {t_{{\rm{sh}}}}{V_{{\rm{sh}}}}$ | (12) |
| ${V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}} + {V_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}} \leqslant 1 - {V_{{\rm{sh}}}} - {V_{\rm{w}}} - {V_{{\rm{ma}}}}$ | (13) |
| $0 \leqslant {V_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{V_{{\rm{C}}{{\rm{H}}_{\rm{4}}}}} \le 1 - {V_{{\rm{sh}}}} - {V_{\rm{w}}} - {V_{{\rm{ma}}}} $ | (14) |
式中:$V_{\rm{ma}}$、$V_{\rm{sh}}$、$V_{\rm{w}}$、$V_{\rm{CH_4}}$、 $V_{\rm{CO_2}}$—各部分体积分数,无因次,且前3个为已知;
$\rho_{\rm{ma}}$、$\rho_{\rm{sh}}$、$\rho_{\rm{w}}$、$\rho_{\rm{CH_4}}$、 $\rho_{\rm{CO_2}}$—各部分密度,g/cm$^{3}$;
$\Delta t_{\rm{ma}}$、$\Delta t_{\rm{sh}}$、$\Delta t_{\rm{w}}$、$\Delta t_{\rm{CH_4}}$、 $\Delta t_{\rm{CO_2}}$—各部分纵波时差,$\mu $m/ft;
下标:ma—岩石骨架,sh—泥质,w—水,CH$_4$—甲烷,CO$_2$—二氧化碳。
式(9)和式(11)为运用密度体积物理模型建立的最优化表达式,其涵义为岩石各部分密度之和从负方向无限接近于密度测井值,式(10)和式(12)为运用纵波时差体积物理模型建立的最优化表达式,其涵义为岩石各部分纵波时差之和从负方向无限接近于纵波时差测井值。
式(13)和式(14)为未知变量的取值范围。按照上述模型,用最优化程序对测井数据进行处理,取4种不同逼近方向结果的平均值,可以得到二氧化碳气体和甲烷气体的体积分数随深度变化的分布曲线。
3 应用实例图 3为南海地区某气田X-6井测井解释成果图,第3道中子与密度的镜像重叠现象显示出气层特征。第5道为运用中子长短源距计数率法求得的甲烷含量,曲线数值表示甲烷体积占气体总体积的百分数,从图中可以看出,3种模型的计算值差异很小,故可用3种模型所得结果的平均值作为这种方法的结论值;第4道为运用最优化算法得到的各气体成分比例,甲烷和二氧化碳填充区域分别表示其占孔隙总体积的百分数。
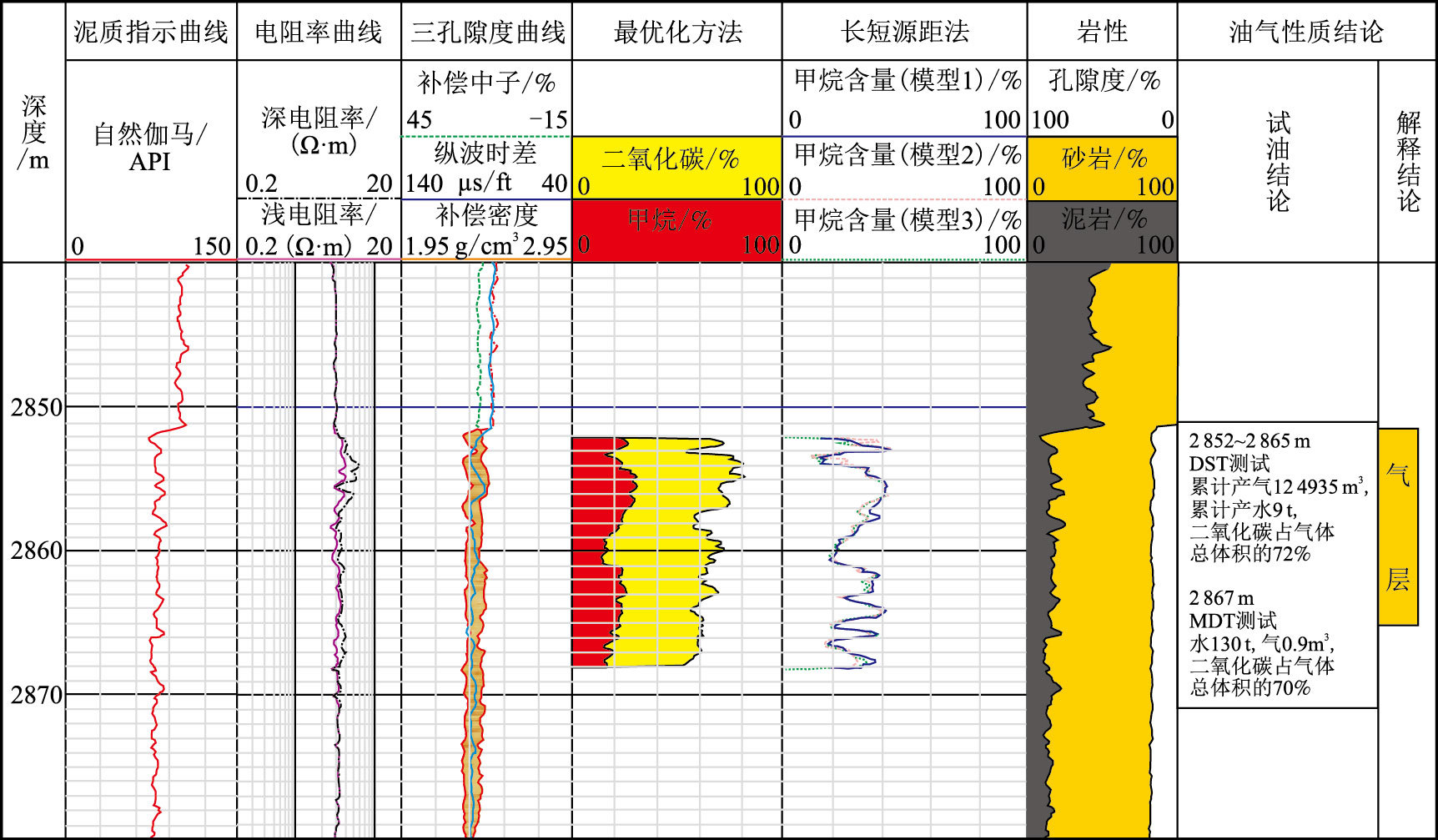 |
| 图3 南海某气田X-6井二氧化碳定量计算测井解释成果图 Fig. 3 Logging interpretation result of CO$_2$ content calculation of Well X-6 in some gas field of South China Sea |
表 1为测井解释二氧化碳含量与试油结论二氧化碳含量对比统计表,从表中可以看出,两种解释方法计算得到的二氧化碳含量均与试油结论接近,最大误差为7.08%,说明运用中子长短源距计数率法和体积物理模型最优化方法在计算二氧化碳含量方面具有较高的精度。
| 表1 试油二氧化碳含量与测井解释二氧化碳含量对比表 Table 1 Comparison of CO$_2$ content from test and logging interpretation results |
(1) 运用中子长短源距计数率建立的3种计算模型均能较为准确地反映出二氧化碳含量的真实情况,说明S型曲线或多项式均能够模拟二氧化碳含量与长短源距计数率的关系,计算结果也说明,除热中子减速作用外,热中子扩散作用对二氧化碳和甲烷的影响也存在一定差异。
(2) 在三孔隙度曲线质量足够好的情况下,运用基于岩石体积物理模型的最优化方法可以避开岩石成分及不同孔隙流体复杂的导电机理,综合提取多条测井曲线的特征,由于含水饱和度已经通过其他测井曲线算出,因此,在束缚水饱和度较高的气层也可以较准确地计算出各气体成分百分含量。
| [1] |
张伙兰, 裴健翔, 张迎朝, 等. 莺歌海盆地东方区中深层黄流组超压储集层特征[J].
石油勘探与开发, 2013, 40 (3) : 284 –293.
ZHANG Huolan, PEI Jianxiang, ZHANG Yingzhao, et al. Overpressure reservoirs in the mid-deep Huangliu Formation of the Dongfang Area, Yinggehai Basin, South China Sea[J]. Petroleum Exploration and Development, 2013, 40 (3) : 284 –293. |
| [2] |
谢玉洪, 范彩伟. 莺歌海盆地东方区黄流组储层成因新认识[J].
中国海上油气, 2010, 22 (6) : 355 –359.
XIE Yuhong, FAN Caiwei. Some new knowledge about the origin of Huangliu Formation reservoirs in Dongfang Area, Yinggehai Basin[J]. China Offshore Oil and Gas, 2010, 22 (6) : 355 –359. |
| [3] |
韩宏伟, 张金功, 张建锋, 等. 济阳拗陷二氧化碳气藏地下相态特征研究[J].
西北大学学报(自然科学版), 2010, 40 (3) : 493 –496.
HAN Hongwei, ZHANG Jingong, ZHANG Jianfeng, et al. A study on phase of CO2 pools underground, Jiyang Depression[J]. Journal of Northwest University (Natural Science Edition), 2010, 40 (3) : 493 –496. |
| [4] |
罗智, 刘如敏, 郝晓良, 等. 利用测录井资料识别气藏中的二氧化碳[J].
内蒙古石油化工, 2012 (9) : 36 –37.
LUO Zhi, LIU Rumin, HAO Xiaoliang, et al. Identification of CO2 in gas reservoir by logging data[J]. Inner Mongolia Petrochemical Industry, 2012 (9) : 36 –37. |
| [5] |
罗智, 张恒山. 利用测井资料识别气藏中的CO2[J].
天然气勘探与开发, 2012, 35 (4) : 34 –35.
LUO Zhi, ZHANG Hengshan. Logging data used to identify CO2 in gas reservoirs[J]. Natural Gas Exploration & Development, 2012, 35 (4) : 34 –35. |
| [6] |
郭宇航, 潘保芝. 松南深层火山岩CO2气层测井特征与含量预测[J].
国外测井技术, 2012 (6) : 24 –27.
GUO Yuhang, PAN Baozhi. Logging identification and content prediction of CO2 bearing reservoirs in deep volcanic in south Songliao Basin[J]. World Well Logging Technology, 2012 (6) : 24 –27. |
| [7] |
郭栋. CO2气综合勘探技术及实例分析[J].
油气地球物理, 2009, 7 (1) : 24 –28.
GUO Dong. Integrated exploration techniques for CO2 and analysis on case history[J]. Petroleum Geophysics, 2009, 7 (1) : 24 –28. |
| [8] |
郭栋. CO2气综合识别技术及应用[J].
物探与化探, 2008, 32 (3) : 283 –287.
GUO Dong. Integranted recognition technique for CO2 gas and its application[J]. Geophysical and Geochemical Exploration, 2008, 32 (3) : 283 –287. |
| [9] |
刘中奇, 杜春玲. 非烃类气层测井识别方法[J].
测井技术, 1998, 22 (2) : 107 –110.
LIU Zhongqi, DU Chunling. Identification of non hydrocarbon Gas Zone[J]. Well Logging Technology, 1998, 22 (2) : 107 –110. |
| [10] |
孟祥水, 张晋言, 孙波. 利用测井视孔隙度差异识别二氧化碳和烃类气[J].
测井技术, 2003, 27 (2) : 132 –135.
MENG Xiangshui, ZHANG Jinyan, SUN Bo. Using different logging apparent porosities to distinguish carbon dioxide from methane[J]. Well Logging Technology, 2003, 27 (2) : 132 –135. |
| [11] | 姜亮,刘大能,邱细斌. 二氧化碳气层的测井解释方法[C]//姜亮. 东海陆架盆地油气资源勘探论文集. 北京:石油工业出版社, 2004:266-271. |
| [12] |
侯大力, 孙雷, 潘毅, 等. 人工神经网络预测高含CO2天然气的含水量[J].
西南石油大学学报(自然科学版), 2013, 35 (4) : 121 –125.
HOU Dali, SUN Lei, PAN Yi, et al. Predicting water content of high CO2 content natural gas by artificial neural network[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35 (4) : 121 –125. |
| [13] |
程超, 桑琴, 杨双定, 等. 最优化测井解释方法在复杂碎屑岩储层中的应用[J].
测井技术, 2011, 30 (5) : 455 –459.
CHENG Chao, SANG Qin, YANG Shuangding, et al. Application of the optimization log interpretation method to complex clastic resservoir[J]. Well Logging Technology, 2011, 30 (5) : 455 –459. |
| [14] |
韩雪, 潘保芝, 张意, 等. 遗传最优化算法在砂砾岩储层测井评价中的应用[J].
测井技术, 2012, 36 (4) : 392 –396.
HAN Xue, PAN Baozhi, ZHANG Yi, et al. GA-optimal log interpretation applied in glutenite reservoir evaluation[J]. Well Logging Technology, 2012, 36 (4) : 392 –396. |
| [15] |
王辉, 周承刚, 孙少平. 测井解释最优化方法中的误差和约束条件[J].
中国煤田地质, 2002, 14 (1) : 73 –76.
WANG Hui, ZHOU Chenggang, SUN Shaoping. Error and constraint condition in the optimization method of logging interpretation[J]. Coal Geology of China, 2002, 14 (1) : 73 –76. |
| [16] |
冯国庆, 陈军, 张烈辉, 等. 最优化测井解释的遗传算法实现[J].
天然气工业, 2002, 22 (6) : 48 –51.
FENG Guoqing, CHEN Jun, ZHANG Liehui, et al. Realizing genetic algorithm of optimal log interpretation[J]. Natural Gas Industry, 2002, 22 (6) : 48 –51. |
| [17] |
段亚男, 潘保芝, 韩雪. 砂砾岩储层的多组分模型及最优化测井解释[J].
国外测井技术, 2012 (6) : 20 –23.
DUAN Ya'nan, PAN Baozhi, HAN Xue. Multicomponent model and optimization logging evaluation of glutinite reservoirs[J]. World Well Logging Technology, 2012 (6) : 20 –23. |
| [18] |
田云英, 夏宏泉. 基于多矿物模型分析的最优化测井解释[J].
西南石油学院学报, 2006, 28 (4) : 8 –11.
TIAN Yunying, XIA Hongquan. The optimal logging explanation based on multi-minerals model analysis[J]. Journal of Southwest Petroleum Institute, 2006, 28 (4) : 8 –11. |
| [19] |
周改英, 赵喜亮. 多矿物模型分析的最优化测井解释[J].
河南石油, 2006, 19 (5) : 21 –22.
ZHOU Gaiying, ZHAO Xiliang. Optimum logging interpretation for multimineral model analysis[J]. Henan Petroleum, 2006, 19 (5) : 21 –22. |
| [20] |
王拥军, 夏宏泉, 陈科贵, 等. 塔里木碳酸盐岩储层最优化测井解释方法[J].
西南石油学院学报, 2000, 22 (4) : 18 –21.
WANG Yongjun, XIA Hongquan, Chen Kegui, et al. Optimized log interpretation for carbonate reservoirs in Tarim Basin[J]. Journal of Southwest Petroleum Institute, 2000, 22 (4) : 18 –21. |
| [21] |
何胜林, 陈嵘, 高楚桥, 等. 乐东气田非烃类气层的测井识别[J].
天然气工业, 2013, 33 (11) : 22 –27.
HE Shenglin, CHEN Rong, GAO Chuqiao, et al. Logging identification of non-hydrocarbon gas zones in the Ledong Gas Field, Yinggehai Basin[J]. Natural Gas Industry, 2013, 33 (11) : 22 –27. |
| [22] |
吴洪深, 高华, 林德明, 等. 南海西部海域非烃类气层测井识别及解释评价方法[J].
中国海上油气, 2012, 24 (1) : 21 –24.
WU Hongshen, GAO Hua, LIN Deming, et al. A methodology on logging identification and interpretation of nonhydrocarbon gas zones in the western South China Sea[J]. China Offshore Oil and Gas, 2012, 24 (1) : 21 –24. |
| [23] |
唐广荣, 赵峰, 李跃林. 东方1-1气田低渗疏松砂岩气藏伤害机理研究[J].
西南石油大学学报(自然科学版), 2015, 37 (3) : 103 –108.
TANG Guangrong, ZHAO Feng, LI Yueli. An experimental study on reservoir damage mechanisms of DF1-1 low permeability loose sandstone gas reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37 (3) : 103 –108. |
 2016, Vol. 38
2016, Vol. 38


