2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500;
3. 中国石油川庆钻探工程有限公司钻采工程技术研究院, 四川 广汉 618300
2. State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. Research Institute of Drilling & Production Engineering Technology, CCDC, Guanghan, Sichuan 618300, China
据统计,在钻井施工中25%以上的溢流/井漏事故直接由钻杆运动产生的波动压力引发。当管柱(钻杆或套管)在充满钻井液的井筒内下行运动时,由于激动压力的作用,造成井内压力大于地层压力,使井筒钻井液进入地层,引发井漏等事故[1]。分析允许钻杆下行速度变化规律,对正确设计井身结构方案,实现微流量(MFC)全过程控压钻井及提高钻井时效均有十分重要的意义[2]。2003年,Santos H等提出了MFC控制钻井的概念,MFC钻井技术除了要求控压设备的精度提高外,还增加了一组MFC地面专用节流管汇,此节流管汇可在起下钻过程中回注钻井液及控制回压[3]。
1934年Cannon G E发现,尽管井筒内液柱产生的压力小于地层压力,钻杆在下行运动过程中,仍然发生了井漏事故[4]。1961年Burkhardt J A[5]对钻杆下行运动引发的激动压力进行了测量。1988年Mitchell R F[6]考虑压力及温度等诸多因素得到了钻杆下行过程中引发激动压力的数值解。中国紧跟国外钻井技术研究步伐[7],从1983年的“六五”国家重大项目,西南石油大学郝俊芳等[8]开始研究起下钻引发的激动压力,并在中原油田全尺寸模拟试验井试验,利用试验装置测量起下钻引发的波动压力及许用钻杆运行速度。起下钻的研究目前仍在继续,并取得了一定的成果[8-15]。
尽管前人对单相钻井液中起下钻引发的波动压力研究较多[16-20],但对气液两相许用钻杆下行速度的研究较少。钻遇高压气层时,井底易发生气侵,现场常采用增大回压或加重钻井液等方法循环出气侵后,进行后续钻井作业。由于循环排出气体耗时较长,从而增大了钻井非工作时间(NPT)。如果借助文中提出的气液两相许用钻杆下行速度半经验模型,采取合理的起下钻速度,在气体全部循环出环空前,进行下钻操作,不仅起到抑制气侵的作用,更可减小钻井的NPT。
1 数学模型为建立许用钻杆下行速度半经验公式,作以下假设[13]: (1) 气液两相间不存在热量及质量交换; (2) 气液两相在井筒中的流动为一维流动; (3) 井筒中气液两相流流型分为泡状流、弹状流及环状流。
1.1 多相流控制方程气相连续方程为
| $\dfrac{\partial }{{\partial t}}\iiint\limits_{{\varOmega _{\text{g}}}} {{\rho _{\text{g}}}{\text{d}}\varOmega } + \iint\limits_{{A_{\text{g}}}} {{\rho _{\text{g}}}{v_{\text{g}}}{n_{\text{g}}}{\text{d}}A} = 0$ | (1) |
式中: t—时间,s;
$\Omega _{\text{g}}$—气相控制体,m3;
$\rho _{\rm g}$—气相密度,kg/m3;
$\Omega$—控制体,m3;
$A _{\rm g}$—气相占控制体的有效横截面积,m2;
$v _{\rm g}$—气相速度,m/s;
$n _{\rm g}$—法线(气相)方向;
A—横截面积,m2。
液相连续方程为
| $\dfrac{\partial }{{\partial t}}\iiint\limits_{{\varOmega _{\text{L}}}} {{\rho _{\text{L}}}{\text{d}}\varOmega } + \iint\limits_{{A_{\text{L}}}} {{\rho _{\text{L}}}{v_{\text{L}}}{n_{\text{L}}}{\text{d}}A} = 0$ | (2) |
式中:
$\Omega _{\text{L}}$—液相控制体,m3;
$\rho _{\rm L}$—液相密度,kg/m3;
$A _{\rm L}$—液相占控制体的有效横截面积,m2;
$v _{\rm L}$—液相速度,m/s;
$n _{\rm L}$—法线(液相)方向。
气相运动方程为
| $\dfrac{\partial }{{\partial t}}\iiint\limits_{{\varOmega _{\text{g}}}} {{\rho _{\text{g}}}{v_{\text{g}}}{\text{d}}\varOmega } + \iint\limits_{{A_{\text{g}}}} {{\rho _{\text{g}}}v_{\text{g}}^{\text{2}}{n_{\text{g}}}{\text{d}}A} = \\{\kern 40pt} \iint\limits_{{A_{\text{g}}}} {p{n_{\text{g}}}dA} - \iiint\limits_{{\Omega _{\text{g}}}} {{\rho _{\text{g}}}{\text{gd}}\varOmega } - {\tau _{{\text{g}}0}}{S_{{\text{g}}0}} - {\tau _{{\text{g}}1}}{S_{{\text{g}}1}}$ | (3) |
式中: p—压力,Pa;
${\tau _{{\text{g}}0}}$—气相与裸眼井壁的摩擦力,Pa;
${S _{{\text{g}}0}}$—气相与裸眼井壁的接触面积,m2;
${\tau _{{\text{g}}1}}$—气相与套管的摩擦应力,Pa;
${A _{{\text{g}}}}$—气相与套管壁的接触面积,m2;
g—重力加速度,g = 9.8 m/s2。
液相运动方程为
| $\dfrac{\partial }{{\partial t}}\iiint\limits_{{\varOmega _{\text{L}}}} {{\rho _{\text{L}}}{\text{d}}\varOmega } + \iint\limits_{{A_{\text{L}}}} {{\rho _{\text{L}}}v_{\text{L}}^{\text{2}}{n_{\text{L}}}{\text{d}}A} = \\{\kern 40pt} \iint\limits_{{A_{\text{L}}}} {p{n_{\text{L}}}{\rm d}A} - \iiint\limits_{{\varOmega _L}} {{\rho _{\text{L}}}{\text{gd}}\varOmega }\! - \!{\tau _{{\text{L0}}}}{S_{{\text{L0}}}}\! -\! {\tau _{{\text{L1}}}}{S_{{\text{L1}}}}$ | (4) |
式中: ${\tau _{{\text{L}}0}}$—液相与裸眼井壁的摩擦力,Pa;
${S _{{\text{L}}0}}$—液相与裸眼井壁的接触面积,m2;
${\tau _{{\text{L}}1}}$—液相与套管的摩擦应力,Pa;
${A _{{\text{L}}}}$—液相与套管壁的接触面积,m2。
1.2 许用钻杆下行速度模型堵口管(关泵)工况下,井筒气-液两相平均流速为[8]
| $\overline v = \left( {\dfrac{{{d^2}}}{{{D^2} - {d^2}}} + {K_{\rm{c}}}} \right){v_{\rm{p}}}$ | (5) |
式中: $\overline v $—平均流速,m/s;
d—钻杆外径,m;
D—井眼直径,m;
$K_{\rm c}$—黏附系数,无因次;
$v_{\rm p}$—钻杆下行速度,m/s。
开口管(关泵)工况下井筒气-液两相平均流速为
| $\overline v = \left( {\dfrac{{{d^2} - d_{\rm{i}}^{\rm{2}}}}{{{D^2} - {d^2}}} + {K_{\rm{c}}}} \right){v_{\rm{p}}} - \dfrac{{40{Q_{\rm{i}}}}}{{{\rm{\pi }}\left( {{D^2} - {d^2}} \right)}}$ | (6) |
式中: $d_{\rm i}$—钻杆内径,m;
$Q_{\rm i}$—钻井液流量,m3/s。
开口管(开泵)工况下,井筒气-液两相平均流速为
| $\overline v = \left( {\dfrac{{{d^2}}}{{{D^2} - {d^2}}} + {K_{\rm{c}}}} \right){v_{\rm{p}}} + \dfrac{{40{Q_{\rm{p}}}}}{{{\rm{\pi }}\left( {{D^2} - {d^2}} \right)}}$ | (7) |
把3种工况管柱与环空气-液两相平均流速的关系表示为函数关系
| $\overline v = F({v_{\rm{p}}})$ | (8) |
根据反函数的定义,有
| ${v_{\rm{p}}} = {F^{ - 1}}(\overline v )$ | (9) |
现场作业中,按照具体工况可以拟合出具体的激动压力公式,利用拟合的激动压力公式可导出许用下钻速度。这里激动压力采用的经验公式为[8]
| ${p_{{\rm{sw}}}} = \dfrac{{0.196{f_{\rm{m}}}{\rho _{\rm{m}}}\overline v^2 {L_{\rm{p}}}}}{{D - d}}$ | (10) |
式中:
$p_{\rm sw}$—激动压力,MPa;
$f_{\rm m}$—摩阻系数,无因次;
$\rho _{\rm m}$—平均流体密度,kg/m3;
$L_{\rm p}$—钻杆长度,m。
安全下钻时,井底的波动压力要小于井底的欠压差,井底欠压差可简化表示为
| $\Delta p = {p_{\rm{p}}} - {p_{\rm{b}}} - {p_{\rm{h}}}$ | (11) |
式中:
$\Delta p$—压差,MPa;
$p_{\rm p}$—地层孔隙压力,MPa;
$p_{\rm b}$—井口回压,MPa;
$p_{\rm h}$—气-液两相静液柱压力,MPa。
联立式(9)~式(11),许用钻杆下行速度为
| ${v_{\rm{p}}} = {F^{ - 1}}\left( {\sqrt {\dfrac{{({p_{\rm{p}}} - {p_{\rm{b}}} - {p_{\rm{h}}})(D - d)}}{{0.196{f_{\rm{m}}}{\rho _{\rm{m}}}{L_{\rm{p}}}}}} } \right)$ | (12) |
以幂律流体为例,层流和紊流中的摩阻系数分别为
| ${f_{\rm{m}}} = \dfrac{{24K{{\left(\dfrac{{2n + 1}}{{3n}}\right)}^{{n}}}}}{{10 \times {{1200}^{1 - {{n}}}}{{(D - d)}^{{n}}}\overline v^2 {\rho _{\rm{m}}}}}$ | (13) |
| ${f_{\rm{m}}} = \dfrac{a}{{{{\left[{\dfrac{{10 \times {{1200}^{1 - {{n}}}}{{(D - d)}^{{n}}}\overline v^2 {\rho _{\rm{m}}}}}{{\dfrac{{0.511{\phi _{300}}}}{{{{511}^{{n}}}}}{{\left( {\dfrac{{2n + 1}}{{3n}}} \right)}^{{n}}}}}} \right]}^{{b}}}}}$ | (14) |
式中: n—流性指数,无因次,$n = 3.322\lg \left( {\dfrac{{{\phi _{600}}}}{{{\phi _{300}}}}} \right)$;
a、b—参数,$a = \dfrac{{\lg n + 3.93}}{{50}}$,$b = \dfrac{{1.75 - \lg n}}{7}$;
$\phi_{300}$、$\phi_{600}$—范式黏度计600 r/min和300 r/min时的读数。
1.3 气液两相参数气体速度计算的经验公式
| ${v_{\rm{g}}} = {{v_{\rm{L}}}\left( {1 - {\phi _{\rm{g}}}} \right) + {v_{\rm{g}}}{\phi _{\rm{g}}}} + {v_{{\rm{sg}}}}$ | (15) |
式中:
$v_{\rm sg}$—气相表观速度,m/s;
$\phi_{\rm g}$—空隙率,%。
钻井液状态方程
| ${\rho _{\rm{L}}} = {\rho _{\rm{L}}}(T,p)$ | (16) |
式中:
T—井筒温度,K。
气体状态方程
| ${\rho _{\rm{g}}} = {\rho _{\rm{g}}}(T,p)$ | (17) |
对于泡状流($\phi_{\rm g} \leqslant 0.25$)液相表观速度为
| ${v_{{\rm{sL}}}} = 1.41{\left[{\dfrac{{\sigma ({\rho _{\rm{L}}} - {\rho _{\rm{g}}})}}{{\rho _{\rm{L}}^{\rm{2}}}}} \right]^{0.25}}$ | (18) |
式中:
$v_{\rm sL}$—液相表观速度,m/s;
$\sigma$—界面张力,N/m。
对于弹状流($\phi_{\rm g}$ > 0.25)液相表观速度为
| ${v_{{\rm{sL}}}} = 0.35{\left[{\dfrac{{\sigma \left( {{\rho _{\rm{L}}} - {\rho _{\rm{g}}}} \right)}}{{\rho _{\rm{L}}^{\rm{2}}}}} \right]^{0.5}}$ | (19) |
气液两相密度、空隙率是本模型求解难点,采用差分方法对式(1)~式(4)求解。允许钻杆下行速度按照式(12)求解。将井筒离散为m个网格,从井底向井口差分计算。
气相连续方程式(1)差分格式为
| $\dfrac{{\left( {A{\rho _{\rm{g}}}{v_{{\rm{sg}}}}} \right)_{i + 1}^{m + 1} - \left( {A{\rho _{\rm{g}}}{v_{{\rm{sg}}}}} \right)_i^{m + 1}}}{{\Delta s}} = \dfrac{{\left( {A{\rho _{\rm{g}}}{\phi _{\rm{g}}}} \right)_i^m}}{{2\Delta t}} + \\{\kern 40pt} \dfrac{{\left( {A{\rho _{\rm{g}}}{\phi _{\rm{g}}}} \right)_{i + 1}^m}}{{2\Delta t}} - \dfrac{{\left( {A{\rho _{\rm{g}}}{\phi _{\rm{g}}}} \right)_i^{m + 1} - \left( {A{\rho _{\rm{g}}}{\phi _{\rm{g}}}} \right)_{i + 1}^{m + 1}}}{{2\Delta t}}$ | (20) |
式中:上标m—网格数;
下标i—时间步。
液相连续方程式(2)差分格式为
| $\dfrac{{\left( {A{v_{{\rm{sL}}}}} \right)_{i + 1}^{m + 1} - \left( {A{v_{{\rm{sL}}}}} \right)_i^{m + 1}}}{{\Delta s}} = \dfrac{{\left( {A{\phi _{\rm{L}}}} \right)_i^m + \left( {A{\phi _{\rm{L}}}} \right)_{i + 1}^m}}{{2\Delta t}} - \\ {\kern 40pt} \dfrac{{\left( {A{\phi _{\rm{L}}}} \right)_i^{m + 1} + \left( {A{\phi _{\rm{L}}}} \right)_{i + 1}^{m + 1}}}{{2\Delta t}}$ | (21) |
两相的动量守恒方程差分格式为
| $\left( {Ap} \right)_{{{i + 1}}}^{{\rm{n + 1}}} - \left( {Ap} \right)_{{i}}^{{{n + 1}}} = {\xi _1} + {\xi _2} + {\xi _3} + {\xi _4}$ | (22) |
| ${\xi _{\rm{2}}} \!=\! \left( {\dfrac{{A{\rho _{\rm{L}}}v_{{\rm{sL}}}^{\rm{2}}}}{{{\phi _{\rm{L}}}}} \!+\! \dfrac{{A{\rho _{\rm{g}}}v_{{\rm{sg}}}^{\rm{2}}}}{{{\phi _{\rm{g}}}}}} \right)_i^{n + 1} - \left( {\dfrac{{A{\rho _{\rm{L}}}v_{{\rm{sL}}}^{\rm{2}}}}{{{\phi _{\rm{L}}}}} \!+\! \dfrac{{A{\rho _{\rm{g}}}v_{{\rm{sg}}}^{\rm{2}}}}{{{\phi _{\rm{g}}}}}} \right)_{i + 1}^{n + 1} $ | (23) |
| ${\xi _{\rm{2}}} \!=\! \left( {\dfrac{{A{\rho _{\rm{L}}}v_{{\rm{sL}}}^{\rm{2}}}}{{{\phi _{\rm{L}}}}} \!+\! \dfrac{{A{\rho _{\rm{g}}}v_{{\rm{sg}}}^{\rm{2}}}}{{{\phi _{\rm{g}}}}}} \right)_i^{n + 1} - \left( {\dfrac{{A{\rho _{\rm{L}}}v_{{\rm{sL}}}^{\rm{2}}}}{{{\phi _{\rm{L}}}}} \!+\! \dfrac{{A{\rho _{\rm{g}}}v_{{\rm{sg}}}^{\rm{2}}}}{{{\phi _{\rm{g}}}}}} \right)_{i + 1}^{n + 1} $ | (24) |
| ${\xi _3} = - \dfrac{{{\rm{g}}\Delta s}}{2}\left[{\left( {A{\rho _{\rm{L}}}} \right)_i^{n + 1} + \left( {A{\rho _{\rm{L}}}} \right)_{i + 1}^{n + 1}} \right]$ | (25) |
| ${\xi _4} = - \dfrac{{\Delta s}}{2}\left[ {A{{\left( {\dfrac{{\partial p}}{{\partial s}}} \right)}_{{\rm{fr}}}}} \right]_i^{n + 1} - \dfrac{{\Delta s}}{2}\left[ {A{{\left( {\dfrac{{\partial p}}{{\partial s}}} \right)}_{{\rm{fr}}}}} \right]_{i + 1}^{n + 1}$ | (26) |
其中:$\phi _{\rm L}$—持液率,%;
$\Delta s$—控制体长度,m;
$\Delta t$—时间步长,s;
${{{\left( {\dfrac{{\partial p}}{{\partial s}}} \right)}_{{\rm{fr}}}}}$—摩阻引起的压降梯度,Pa/m。
由于气液两相许用钻杆下行速度文献较少,故将模型计算的激动压力数值解与参考文献[8]试验测得的试验值对比,如果计算结果与试验值具有一致性,可判断本文的许用钻杆下行速度半经验公式具有可靠性。图 1验证了模型的计算解与文献试验值具有一致性。
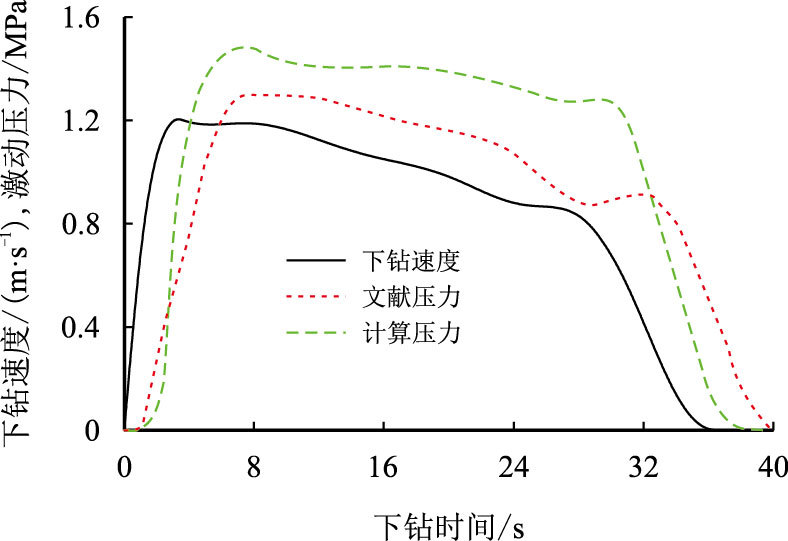 |
| 图1 本文模型计算结果与前人结果对比 Fig. 1 Comparison of calculation results with previous data |
以川内的某口井为例,当该井钻至井深4 000 m时,其井身结构示意图如图 2所示。钻井作业时施工参数为:钻井液密度1 580 kg/m3;管柱弹性模量2.07×105 MPa;管柱泊松比0.3,粗糙度0.001~5 mm;地层温度梯度0.025 ℃/m;钻井液排量28 L/s。
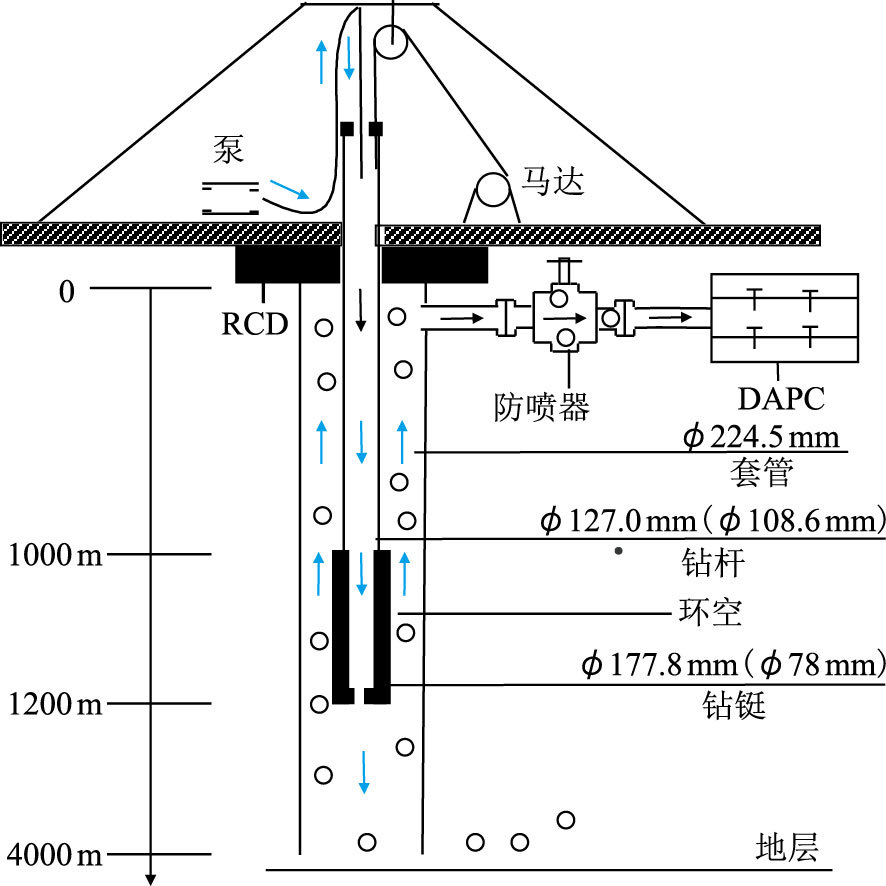 |
| 图2 微流量控制钻井中气液两相钻杆下行作业示意图 Fig. 2 Schematic diagram of gas influx process in tripping during MFC drilling operations |
图 3与图 4给出了不同气侵量(0,1.28,3.09和8.43 m3/h)对井筒的空隙率及许用钻杆下行速度的影响。当井底未发生气侵时,井筒中的空隙率均为0,此时许用下钻速度与气液两相相比,呈减小的趋势。随气侵量的减小,气液两相的空隙率减小,作用于井底有效激动压力增大,因此许用钻杆下行速度减小。在4 000 m井底压力高达50 MPa,气体处于高度压缩状态,其密度、气液两相的黏滞力在井底处变化不大,因此在井底许用钻杆下行速度变化不大。
 |
| 图3 气侵量对空隙率的影响 Fig. 3 Effect of gas influx rate on the void fraction |
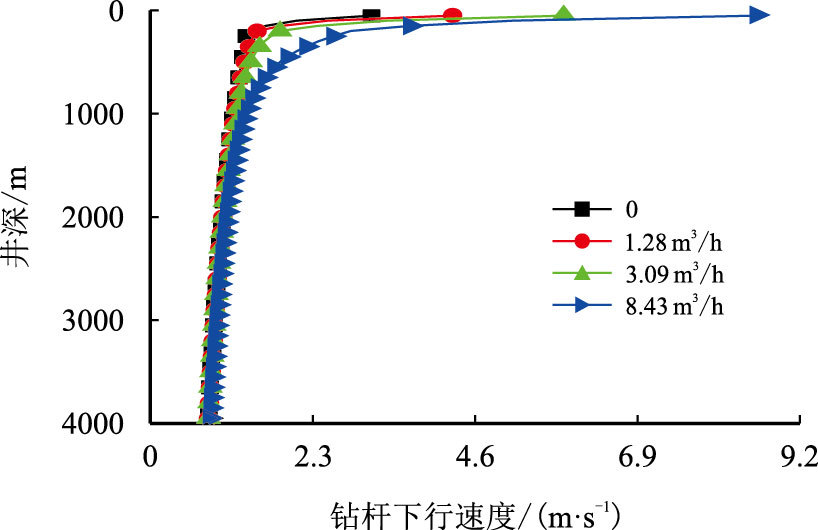 |
| 图4 气侵量对许用钻杆下行速度影响 Fig. 4 Effect of gas influx rate on allowable tripping velocity |
钻井中钻杆下行可能遇到多种工况,如开口管关泵(OC)、堵口管关泵(CC)及开口管开泵(OO),图 5与图 6给出了不同工况对井筒内气液两相平均流速及许用钻杆下行速度的影响($Q_{\rm{g}}$—气相流量,m3/h;$Q_{\rm{L}}$—液相流量,m3/h)。
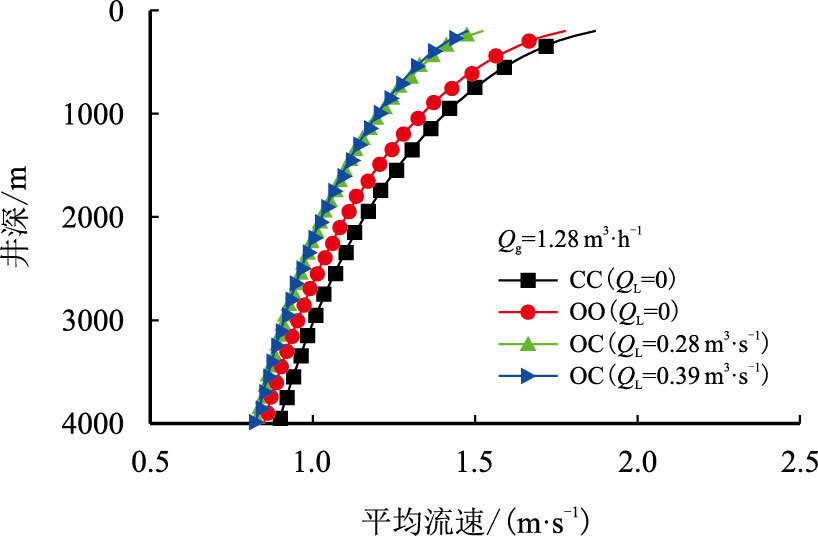 |
| 图5 不同工况对井筒流体平均流速的影响 Fig. 5 Effect of different conditions on average velocity |
图 5及图 6所示的3种工况小排量情况下,堵口管关泵(CC)引起的井筒平均流速比其他两种要大,相应的许用钻杆下行速度减小。根据式(6)及(7)可得开口管关泵(OC)较开口管开泵(OO)所引起的井筒平均流速变化减小,相应的许用钻杆下行速度增大,这是由于开口管关泵(OC)工况下,钻杆下行运动中一部分钻井液进入到钻杆内,使得排开钻井液的有效体积减小,从而引起井筒平均流速减小,使得许用钻杆下行速度增大。
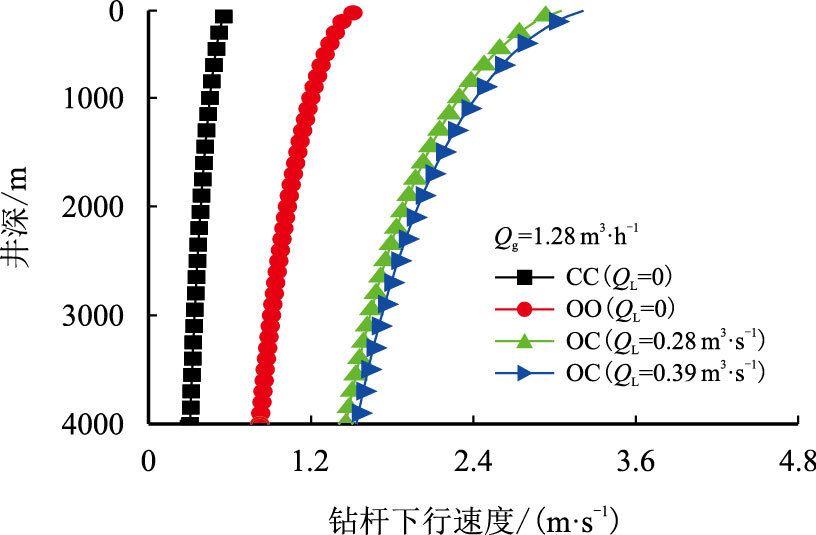 |
| 图6 不同工况对许用钻杆下行速度的影响 Fig. 6 Effect of different conditions on allowable tripping velocity |
图 7与图 8分别给出了不同井底安全压差(1.0,2.0,3.0,4.0 MPa)对井筒气液两相平均流速及许用钻杆下行速度的影响。
井底安全压差是指在钻井时,不使井底出现喷、漏事故的安全压力范围。许用钻杆下行速度取决于钻杆下行允许的激动压力,允许激动压力主要取决于井底安全压差。钻杆作用于钻井液主要由钻杆壁对钻井液的作用,钻井液流动依靠钻井液层间的黏滞力,因此钻井液层间黏滞力与井底安全压差是允许钻杆下行速度的主要影响因素。由图 7与图 8可见,随井底压差的增大,许用激动压力增大,允许钻杆下行排开的钻井液的平均流速增大,许用钻杆下行速度增大。
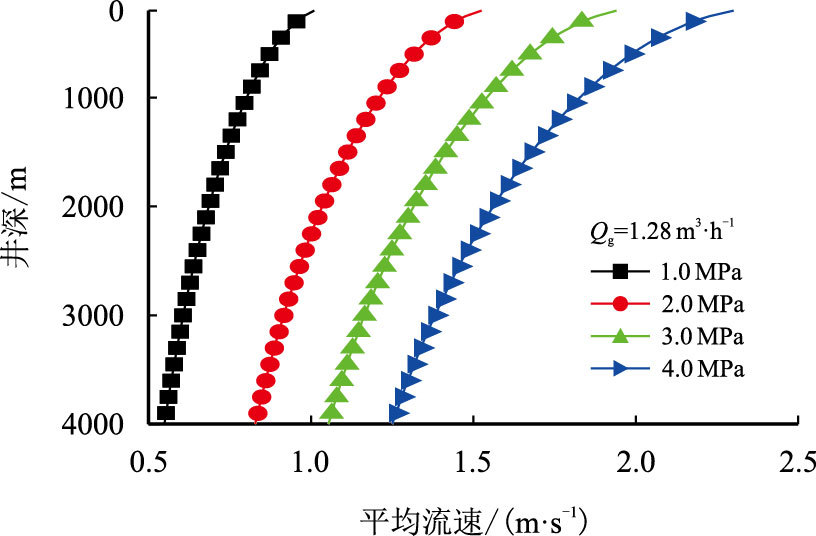 |
| 图7 压差对井筒流体允许平均流速的影响 Fig. 7 Effect of pressure difference on allowable average velocity |
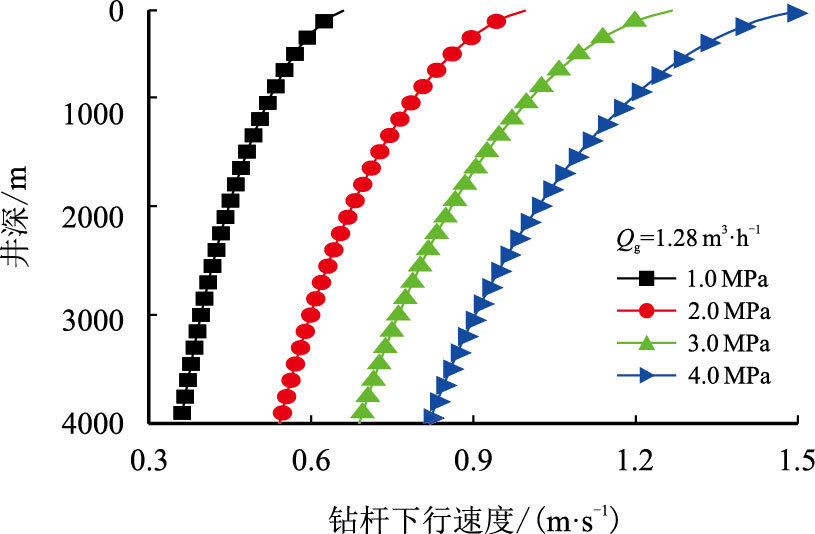 |
| 图8 压差对许用钻杆下行速度的影响 Fig. 8 Effect of pressure difference on allowable tripping velocity |
当井底发生气侵时,通过增大回压或增大钻井液密度的方法控制井底气侵进一步发生,图 9及图 10给出了不同回压(0.1,0.5,2.0,6.0 MPa)对井筒内气体空隙率及许用钻杆下行速度的影响。
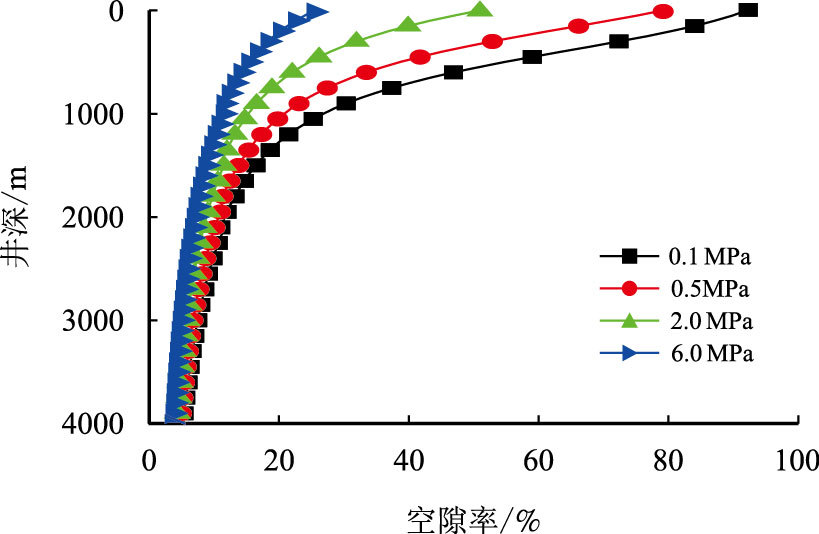 |
| 图9 回压对空隙率的影响 Fig. 9 Effect of BP on the void fraction |
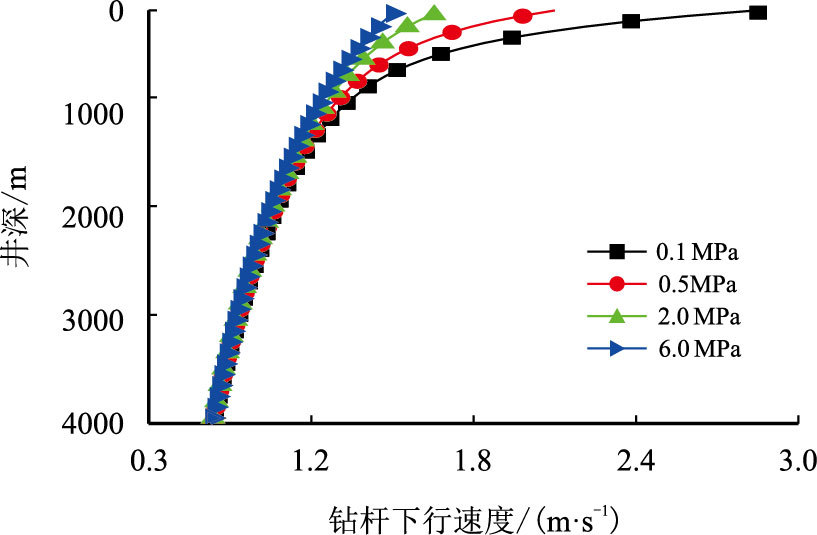 |
| 图10 回压对许用钻杆下行速度的影响 Fig. 10 Effect of BP on allowable tripping velocity |
井口回压增大,增大了井筒内有效压力,使井筒中气体空隙减小,许用钻杆下行速度减小(图 10)。井筒有效压力增大,使井筒中气相的压缩性减小,气体密度增大(图 9),气液两相层间黏滞力增大,因此许用钻杆下行速度增大。相同工况下,随钻杆下行速度减小,引发的激动压力减小,对井底压力的控制有利,然而过小的钻杆下行速度必然引起钻井时效的降低。
4 结论(1) 许用钻杆下行速度取决于钻杆下行过程引起的激动压力、井底压差及液柱静压力等因素,在微流量控制钻井中,要考虑回压对许用钻杆下行速度的影响。
(2) 钻杆下行运动时,排开钻井液的平均速度与许用钻杆速度呈相反趋势。在小排量情况下,开口管关泵、堵口管关泵及开口管开泵3种工况中,堵口管关泵中钻杆排开的钻井液量最大,所引起的井筒平均流速增大,激动压力最大,从而许用钻杆下行速度减小。
(3) 气侵量增大或回压减小均使井筒中空隙率增大,气液两相密度减小,从而作用于井底的有效液柱压力减小,使许用钻杆下行速度增大。
| [1] | RUBIANDINI R S. New formula of surge pressure for determining safe trip velocities[C]//SPE Asia Pacific Oil and Gas Conference and Exhibition,Society of Petroleum Engineers, 2000. |
| [2] | CRESPO F, AHMED R. A simplified surge and swab pressure model for yield power law fluids[J]. Journal of Petroleum Science and Engineering, 2013, 101 : 12 –20. DOI:10.1016/j.petrol.2012.10.001 |
| [3] | SANTOS H, LEUCHTENBERG C, SHAYEGI S. Micro-flux control:the next generation in drilling process[C]//SPE Latin American and Caribbean Petroleum Engineering Conference. Society of Petroleum Engineers, 2003. |
| [4] | CANNON G E. Changes in hydrostatic pressure due to withdrawing drill pipe from the hole[J]. Drilling and Production Practice, 1934 . |
| [5] | BURKHARDT J A. Wellbore pressure surges produced by pipe movement[J]. Journal of Petroleum Technology, 1961, 13 (6) : 595 –605. DOI:10.2118/1546-G-PA |
| [6] | MITCHELL R F. Dynamic surge/swab pressure predictions[J]. SPE Drilling Engineering, 1988, 3 (03) : 325 –333. DOI:10.2118/16156-PA |
| [7] | SUN Yuxue, LI Qiming, ZHAO Jingyuan. New method of predicting surge pressure apply to horizontal well based on casson flow[J]. Natural Science, 2010, 2 (12) : 1394 –1399. DOI:10.4236/ns.2010.212170 |
| [8] |
郝俊芳.
平衡钻井与井控[M]. 北京: 石油工业出版社, 1992 .
HAO Junfang. Balanced drilling and well control[M]. Beijing: Petroleum Industry Press, 1992 . |
| [9] |
樊洪海. 起下钻动态波动压力应用软件开发[J].
石油钻探技术, 1995, 23 (4) : 11 –14.
FAN Honghai. Development of application software for dynamic surge pressure while tripping[J]. Petroleum Drilling Techniques, 1995, 23 (4) : 11 –14. |
| [10] | RASMUSSEN O S, SANGESLAND S. Evaluation of MPD methods for compensation of surge and swab pressures in floating drilling operations[C]. IADC/SPE Managed Pressure Drilling & Underbalanced Operations, 2007. |
| [11] | CRESPO F E, AHMED R M, SAASEN A, et al. Surge-and-swab pressure predictions for yield-power-law drilling fluids[J]. SPE Drilling & Completion, 2012, 27 (4) : 574 –585. |
| [12] | WANG S J, CAO Q, BO K. Fluctuating pressure calculation during the progress of trip in managed pressure drilling[J]. Advanced Materials Research, 2012, 468 : 1736 –1742. |
| [13] |
FAN Jun. Oil and gas wells dynamic model of well control theory, and computer simulation[D]. Nanchong:Southwest Petroleum institute, 1998.
范军,油气井动态井控理论模型及计算机仿真研究[D]. 南充:西南石油学院, 1998. |
| [14] |
陈家琅, 陈涛平.
石油气液两相管流[M]. 北京: 石油工业出版社, 2010 .
CHEN Jialang, CHEN Taoping. Petroleum gas-liquid two-phase pipe flow[M]. Beijing: Petroleum Industry Press, 2010 . |
| [15] | KONG X, LIN Y, QIU Y, et al. A new model for predicting dynamic surge pressure in gas and drilling mud two-phase flow during tripping operations[C]. Mathematical Problems in Engineering, 2014. |
| [16] |
平立秋, 汪志明, 魏建光. 欠平衡钻井多相流模型评价分析[J].
西南石油大学学报(自然科学版), 2007, 29 (1) : 75 –78.
PING Liqiu, WANG Zhiming, WEI Jianguang. The evaluation of multiphase phase flow in under balanced driling[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2007, 29 (1) : 75 –78. |
| [17] |
石磊. 一种新型滑套开关工具及配套技术应用研究[J].
西南石油大学学报(自然科学版), 2014, 36 (1) : 157 –162.
SHI Lei. Application research on a new technology of shifting sleeves[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36 (1) : 157 –162. |
| [18] | PÁLSSON B, HÓLMGEIRSSON S, GUDMUNDSSON Á, et al. Drilling of the well IDDP-1[J]. Geothermics, 2014, 49 : 23 –30. DOI:10.1016/j.geothermics.2013.08.010 |
| [19] | SANTOSO B. Pipeline leak detection in two phase flow based on fluctuation pressure difference and artificial neural network(ANN)[J]. Applied Mechanics and Materials, 2014, 493 : 186 –191. DOI:10.4028/www.scientific.net/AMM.493 |
| [20] | CAYEUX E, DAIREAUX B, DVERGSNES E. Automation of drawworks and topdrive management to minimize swab/surge and poor-downhole-condition effect[J]. SPE Drilling & Completion, 2011, 26 (4) : 557 –568. |
 2016, Vol. 38
2016, Vol. 38


