2. 中国石油长庆油田分公司第六采油厂, 陕西 西安 710018
2. The Sixth Oil Recovery Plant of Changqing Oilfield Company, PetroChina, Xi'an, Shaanxi 710018, China
油田注水是为了保持油层压力和提高采收率,已经是一项成熟的技术。但在注水开发中,尤其是开发中后期,结垢现象普遍存在。作为常见垢之一的硫酸钡垢是由于两种不配伍的水混合引起的。富含硫酸根离子的注入水与含有钡离子的地层水在井底附近以一定流速充分混合,发生沉淀反应,其沉淀物堵塞孔隙导致渗透率下降,降低了注水井的吸水能力和油井产量,极大地影响了油田正常生产。
硫酸钡结垢预测已从定性的饱和指数法发展为考虑化学动力学原理的动态结垢模型。文献[1-2]对硫酸钡结垢动态模型进行了研究。
但是,在模型的求解过程中,对离子浓度比作出了远小于1的假设。而在近年来出现的深海油田注水开发过程中,一方面,其地层水中的钡离子浓度很高,可以达到700 mg/L以上[3];另一方面,由于周期性挤注阻垢剂的成本高且在水下复杂采油系统中实施挤注风险高,实际开发过程采用了预先处理后的低硫酸根离子浓度的海水作为注入水[4-10]。显然,研究这类油田的结垢时,近井地带边界处钡离子与硫酸根离子浓度比远小于1的假设是不适宜的。因此,本文详细推导了地层结垢模型,修正了控制方程中二阶项的系数,改进了求解方法,并研究用低硫酸根离子浓度水作为注入水时的阻力系数以及不同参数对阻力系数的影响。
1 地层结垢模型的推导 1.1 模型假设条件(1) 模型尺度设为近井地带[11-12],通常为距离井底10 m的范围;
(2) 地层为均质等厚;
(3) 地层中的油水渗流为等温稳态平面径向流,距离井眼不同半径处截面上的径向流量相同;
(4) 近井地带边界处的钡离子与硫酸根离子浓度在注水过程中不变;
(5) 注入水与地层水视为不可压缩,离子在各个方向上的扩散系数、反应系数相同。
1.2 质量守恒方程含有硫酸根的注入水与含有钡离子地层水在近井地带混合流动过程中,离子量的变化遵循质量守恒定律,在近井地带距离一口单井的井眼中心R处取某一单元体,在任意瞬态下的质量守恒关系为
| $\Delta n = - \Delta n_1 - \Delta n_2 - \Delta n_3$ | (1) |
式中:
$\Delta n$- 单元体内离子量的变化; $\Delta n_1$- 从各个方向沿边界外法线方向流出的量; $\Delta n_2$- 从各个方向沿边界外法线方向扩散出的量; $\Delta n_3$- 单元体内部沉淀反应减少的量。
1.2.1 近井地带浓度变化的控制方程以地层中某一微元体中的钡离子为对象,其物质的量的变化满足质量守恒方程
| $\begin{array}{l} \int\limits_V {\phi S\frac{{\partial {C_{{\rm{Ba}}}}}}{{\partial t}}{\rm{d}}V} = - \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_A { - {D^{{\rm{eff}}}}S\frac{{\partial {C_{{\rm{Ba}}}}}}{{\partial \vec n}}{\rm{d}}A} - \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_A {{C_{{\rm{Ba}}}}S\vec u{\rm{d}}A} \\ - \int\limits_V {K{a^{{\rm{eff}}}}{C_{{\rm{Ba}}}}{C_{{\rm{S}}{{\rm{O}}_{\rm{4}}}}}{\rm{d}}V} \end{array} $ | (2) |
式中:
$C_{{\rm{Ba}}}$- 钡离子浓度,mol/L;
$C_{{\rm{SO}}_{\rm{4}}}$- 硫酸根离子浓度,mol/L;
φ- 孔隙度,%;
S- 含水饱和度,%;
V- 某一微元体体积,m3;
A- 某一微元体表面积,m2;
t- 时间,s;
u- 注入水、地层水混合后的流体径向渗流速度,m/s;
$Ka^{\rm{eff}}$- 多孔介质中离子等效反应系数,L/(mol·s);
$D^{\rm{eff}}$- 多孔介质中离子等效扩散系数,m2/s。
单元体内钡离子量的变化$\Delta n$为
| $\Delta n = \int\limits_V {\phi S\dfrac{{\partial C_{{\rm{Ba}}} }}{{\partial t}}{\rm{d}}V} {\rm{ = }}2\pi Rh\phi S\dfrac{{\partial C_{{\rm{Ba}}} }}{{\partial t}}{\rm{d}}R$ | (3) |
式中: R- 径向半径,m。
从各个方向沿边界外法线方向扩散出的钡离子量$\Delta n_2$为
| $\begin{array}{l} \Delta {n_2} = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_A { - {D^{{\rm{eff}}}}S\frac{{\partial {C_{{\rm{Ba}}}}}}{{\partial \vec n}}{\rm{d}}A} = {\rm{ = }}\int\limits_V {{D^{{\rm{eff}}}}S{{\vec \nabla }_{\rm{r}}} \cdot \left( {\frac{{\partial {C_{{\rm{Ba}}}}}}{{\partial R}}} \right)} {\rm{d}}V\\ = 2\pi h\frac{\partial }{{\partial R}}\left( {{D^{{\rm{eff}}}}SR\frac{{\partial {C_{{\rm{Ba}}}}}}{{\partial R}}} \right){\rm{d}}R \end{array}$ | (4) |
径向渗流速度$\vec u$满足
| $\vec u{\rm{ = }}\vec Qf/2\pi RSh$ | (5) |
式中:
$\vec n$- 表面积法向量,无因次;
$\vec \nabla _{\rm{r}}$- 梯度算子,无因次;
$\vec Q$- 径向半径R处流量,m3/s;
f- 产水率,%;
h- 地层厚度,m。
由于地层水(含钡离子)压缩系数很小,随着压力和温度变化,密度仅有微小的变化,在此可视为不可压缩流,因此从各个方向沿边界外法线方向流出的钡离子量$\Delta n_1$为
| $\begin{align} & \Delta {{n}_{1}}=\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_A {{C}_{\text{B a}}}S\vec{n}\cdot \vec{u}\text{d}A =\int\limits_{V}{{{{\vec{\nabla }}}_{\text{r}}}\cdot ({{C}_{\text{B a}}}S\vec{u})}\text{d}V= \\ & {{{\vec{\nabla }}}_{\text{r}}}({{C}_{\text{B a}}}S)\cdot \frac{\vec{Q}\text{ }f}{2\pi Rsh}2\pi Rh\text{d}R\text{=}Q\text{ }f\frac{\partial {{C}_{\text{B a}}}}{\partial R}\text{d}R \\ \end{align}$ | (6) |
假设硫酸钡沉淀反应为2级反应,单元体内钡离子由于发生沉淀反应减少的量$\Delta n_3$为
| $\Delta n_3=\int\limits_V{Ka^{\rm{eff}}C_{{\rm{B}}{\rm{a}}}c_{{\rm{S}} {\rm{O}}_{\rm{4}}}S{\rm{d}}V}=Ka^{\rm{eff}}C_{{\rm{B}} {\rm{a}}}C_{{\rm{S}}{\rm{O}}_{\rm{4}}}2\pi RhS{\rm{d}}R $ | (7) |
在稳态流动下,式(3)恒为0。将式(4)、式(6)、式(7)代入质量守恒方程,整理,得钡离子控制方程
| $Q f\dfrac{{\partial C_{{\rm{B}}{\rm{a}}} }}{{\partial R}} = 2 \pi h\dfrac{\partial }{{\partial R}}\bigg(D^{\rm{eff}} S R\dfrac{{\partial C_{{\rm{B}} {\rm{a}}} }}{{\partial R}}\bigg) - 2\pi Rh S Ka^{\rm{eff}} C_{{\rm{B}} {\rm{a}}} C_{{\rm{S}}{\rm{O}}_{{\rm{4}}} }$ | (8) |
引入变换
| $\left\{ \begin{array}{l} \rho {\rm{ = }}\dfrac{R}{{R_{\rm{c}} }} \\ C = \dfrac{{C_{{\rm{B}}{\kern 1pt} {\rm{a}}} }}{{C_{{\rm{B}} {\rm{a}}}^0 }}\\ \alpha = \dfrac{{C_{{\rm{B}} {\rm{a}}}^0 }}{{C_{{\rm{S}} {\rm{O}}_{\rm{4}} }^0 }} \\ Y_\alpha = \dfrac{{C_{{\rm{S}} {\rm{O}}_{\rm{4}} } }}{{C_{{\rm{S}} {\rm{O}}_{\rm{4}} }^0 }}\dfrac{1}{\alpha } = Y\dfrac{1}{\alpha } \\ T = \dfrac{{Q t}}{{\pi R_{ {\rm{c}}}^{ 2} h \phi }} \\ U = \left| {\vec u } \right|{\rm{ = }}\dfrac{{Q f}}{{2 \pi R h s}} \\ D^{\rm{eff}} = \varepsilon _{\rm{c}} R_{ {\rm{c}}} U \\ Ka^{\rm{eff}} = \lambda U \\ \varepsilon _{{\rm{k}} }^{} = R _{\rm{c}} \lambda C_{{\rm{S}} {\rm{O}}_{ {\rm{4}}} }^0 \\ \end{array} \right.$ | (9) |
式中:
$\rho$- 距离井眼中心的无因次半径;
$R_{\rm{c}}$- 近井地带边界半径,m;
C- 无因次钡离子浓度;
Y- 无因次硫酸根离子浓度;
$Y_\alpha$- 无因次硫酸根离子浓度与α的比值,无因次;
U- 无因次渗流速度;
$C_{_{{\rm{Ba}}} }^0 $- 近井地带边界处的钡离子浓度,mol/L;
$C_{_{{\rm{SO}}_{\rm{4}} } }^0 {\kern 1pt} $- 近井地带边界处的硫酸根离子浓度,mol/L;
α- 近井地带边界处钡离子与硫酸根离子的浓度比,%;
T- 无因次时间;
λ- 化学反应强度系数,L/(mol·m);
$\varepsilon_{\rm{c}}$- 无因次扩散系数;
$\varepsilon_{\rm{k}}$- 无因次反应系数。
式(9)代入式(8)可,得
| $\begin{align} & Qf\frac{\partial C}{{{R}_{\text{c}}}\partial \rho }=2\pi h\frac{\partial }{{{R}_{\text{c}}}\partial \rho }\left( {{D}^{\text{eff}}}S\rho \frac{\partial C}{\partial \rho } \right)-(2\pi U\rho hS)({{R}_{\text{c}}}\lambda C_{\text{Ba}}^{0})C{{Y}_{\alpha }}= \\ & 2\pi h\frac{\partial }{{{R}_{\text{c}}}\partial \rho }\left( {{\varepsilon }_{\text{c}}}{{R}_{\text{c}}}SU\rho \frac{\partial C}{\partial \rho } \right)-\left( \frac{Qf}{{{R}_{\text{c}}}} \right)({{R}_{\text{c}}}\lambda C_{\text{Ba}}^{0})C{{Y}_{\alpha }}= \\ & \frac{\partial }{{{R}_{\text{c}}}\partial \rho }\left( {{\varepsilon }_{\text{c}}}{{R}_{\text{c}}}\frac{Qf}{{{R}_{\text{c}}}}\frac{\partial C}{\partial \rho } \right)-\left( \frac{Qf}{{{R}_{\text{c}}}} \right)({{R}_{\text{c}}}\lambda C_{\text{Ba}}^{0})C{{Y}_{\alpha }}= \\ & \frac{Qf}{{{R}_{\text{c}}}}\frac{{{\varepsilon }_{\text{c}}}{{R}_{\text{c}}}\partial }{{{R}_{\text{c}}}\partial \rho }\left( \frac{\partial C}{\partial \rho } \right)-\left( \frac{Qf}{{{R}_{\text{c}}}} \right)({{R}_{\text{c}}}\lambda C_{\text{Ba}}^{0})C{{Y}_{\alpha }}= \\ & \frac{Qf}{{{R}_{\text{c}}}}{{\varepsilon }_{\text{c}}}\frac{\partial }{\partial \rho }\left( \frac{\partial C}{\partial \rho } \right)-\left( \frac{Qf}{{{R}_{\text{c}}}} \right){{\varepsilon }_{\text{k}}}\alpha C{{Y}_{\alpha }}n \\ \end{align}$ | (10) |
整理得,关于无因次钡离子浓度的控制方程
| $\dfrac{{\partial C}}{{\partial \rho }} = \varepsilon _{\rm{c}} \dfrac{{\partial ^2 C}}{{\partial \rho ^2 }} - \varepsilon _{\rm{k}}^{} \alpha CY_\alpha$ | (11) |
由上述推导过程可以看出,式(11)中的二阶项系数应该为$\varepsilon_{\rm{c}}$,而不是无因次扩散系数与饱和度的乘积[2]。
1.3 修正二阶项系数后的地层结垢模型与阻力系数类似地,可以推导出关于无因次硫酸根离子浓度的控制方程
| $\dfrac{{\partial Y_\alpha }}{{\partial \rho }} = \varepsilon _{\rm{c}} \dfrac{{\partial ^2 Y_\alpha }}{{\partial \rho ^2 }} - \varepsilon _{\rm{k}}^{} \alpha CY_\alpha$ | (12) |
关于无因次硫酸钡沉淀浓度的控制方程为
| $\dfrac{{\partial \sigma }}{{\partial T}} = \varepsilon _{\rm{k}}^{} \alpha CY_\alpha$ | (13) |
稳态流动下的边界条件为
| $\left\{ \begin{array}{l} \dfrac{{\partial C}}{{\partial \rho }} = \dfrac{{\partial Y_\alpha }}{{\partial \rho }} = 0 ~~~~~~\mbox{内边界条件} \rho = \dfrac{{r_{\rm{w}} }}{{R_{\rm{c}} }}\\ C = 1, Y_\alpha = 1/\alpha ~~~~~~\mbox{外边界条件} \rho = 1\\ \end{array} \right.$ | (14) |
式(11)~式(14)构成了完整的地层硫酸钡结垢预测模型。
由于硫酸钡结垢会堵塞孔隙,造成渗透率下降,采油指数就会随着结垢量增加而下降。采油指数随着无因次时间下降的快慢程度可以由阻力系数来表示[12-14],即
| $m \buildrel \Delta \over = F(T) = \dfrac{{\beta R_{\rm{c}} \lambda C_{_{{\rm{B}} {\rm{a}}} }^0 f}}{{2 \ln \dfrac{{R_{\rm{c}} }}{{r_{\rm{w}} }} S}}\int_{\frac{{r_{\rm{w}} }}{{R_{\rm{c}} }}}^1 {\dfrac{{C(\rho )Y_\alpha (\rho )}}{{\rho ^2 }}{\rm{d}}\rho }$ | (15) |
式中:
$\beta$- 储层损害系数,无因次;
$r_{\rm{w}}$- 井眼半径,m。
2 模型求解方法的改进硫酸钡岩芯结垢模型模拟的是在岩芯流动实验中同时用注入水和地层水驱替已饱和地层水的岩芯时的硫酸钡结垢过程。关于模型中的无因次反应系数 $\varepsilon_{\rm{k}}$的求取,原有的解法需要分两步[2, 14]
(1) 在岩芯入口端钡离子与硫酸根离子浓度比α远小于1的假设下,将岩芯结垢模型(17)中钡离子浓度控制方程简化为
| $\varepsilon _{\rm{c}} \dfrac{{{\rm{d}}^2 C}}{{{\rm{d}}X^2 }} = \dfrac{{{\rm{d}}C}}{{{\rm{d}}X}} + \varepsilon _{\rm{k}} C$ | (16) |
然后用渐进法求取线性化后的边值问题的解析解,并将其作为问题(17)的近似解
| $\left\{ \begin{array}{l} \varepsilon _{\rm{c}} \dfrac{{{\rm{d}}^2 C}}{{{\rm{d}}X^2 }} = \dfrac{{{\rm{d}}C}}{{{\rm{d}}X}} + \varepsilon _{\rm{k}} C\left[ {1 + \alpha \left( {C - 1} \right)} \right] \\ C = 1~~~~~~~~~\mbox{内边界条件}X = 0\\ \dfrac{{\partial C}}{{\partial X}} = 0~~~~~~\mbox{外边界条件}X = 1 \\ \end{array} \right.$ | (17) |
(2) 用近似解与实测的出口端浓度拟合得到$\varepsilon_{\rm{k}}$
上述方法求得的近似解表达式繁杂,更重要的是离子浓度比α远小于1的假设使这种方法有很大的局限性。在模拟不同硫酸根离子浓度的注入水与地层水混合时,必须取消这一假设直接对非线性问题(17)进行求解。具体的,首先将(17)改写为一阶常微分方程组(18)
| $ \left\{ \begin{array}{l} \dfrac{{{\rm{d}}C(1)}}{{{\rm{d}}X}} = C(2) \\ \dfrac{{{\rm{d}}C(2)}}{{{\rm{d}}X}} = 1/\varepsilon _{\rm{c}} \left\{ {C(2) + \varepsilon _{\rm{k}} C(1)\left[ {1 + \alpha \left( {C(1) - 1} \right)} \right]} \right\} \\ C(1)\left| {_{X = 0} = 1} \right. \\ C(2)\left| {_{X = 1} = 0} \right. \\ \end{array} \right. $ | (18) |
其中$C(1) = \dfrac{{{\rm{d}}C}}{{{\rm{d}}X}}$。 由于式(18)为带参数的边值问题($\varepsilon_{\rm{k}}$为需要拟合的未知参数),所以还需要一个边界条件才能使该问题闭合
| $C(1)\left| {_{X = 1} = C_{{\rm{med}}} } \right.$ | (19) |
式中:
$C_{{\rm{med}}}$- 出口端实测的钡离子浓度与原始钡离子浓度之比,无因次。
式(19)表示模型计算出的出口端钡离子浓度与实测浓度应该相等。联立式(18)式(19),采用4阶3 步罗巴托法和牛顿迭代法[15, 16]进行数值计算,即可得到$\varepsilon_{\rm{k}}$的值与稳态下的离子浓度与硫酸钡沉淀浓度的分布。对于硫酸钡地层结垢模型的求解,也可类似地取消近井地带边界处离子浓度比远小于1的假设进行求解。
3 计算实例与分析在修正后的地层模型基础上,用新的方法对注水过程中一口单井的近井地带硫酸钡结垢过程进行了计算。分析讨论了不同参数下结垢产生的阻力系数。模型需要的基本参数见表 1。
| 表1 近井地带硫酸钡结垢模型计算基本参数[2] Table 1 Essential parameters for near-well barium sulfate scale model calculation[2] |
根据基本参数,分别计算了不同注入水情况下的各个参数对阻力系数的影响。
(1) 高硫酸根离子浓度的注入水与地层水混合时,不同无因次扩散系数下的近井地带的阻力系数m见图 1。
(2) 低硫酸根离子浓度的注入水与地层水混合时,近井地带边界处钡离子和硫酸根离子浓度比很高,α较大。边界处不同的硫酸根离子浓度对应的α见表 2。
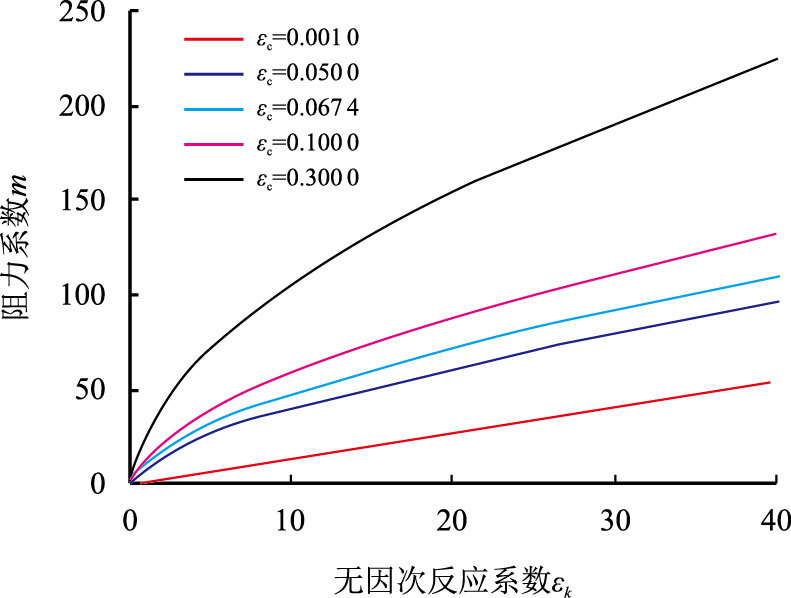 |
| 图1 高硫酸根离子浓度注入水的阻力系数($C_{{\rm{SO}}_4}$=2 800 mg/L) Fig. 1 Impedance coefficient for high sulfate injection water ($C_{{\rm{SO}}_4}$=2 800 mg/L) |
由图 1可以看出,无因次扩散系数$\varepsilon_{\rm{c}}$增大时,多孔介质中的离子扩散更充分,结垢量更大,阻力系数增加;无因次反应系数$\varepsilon_{\rm{k}}$增大时,多孔介质中的沉淀化学反应速率更快,结垢量增大,阻力系数增加。
| 表2 硫酸根离子浓度与对应的边界处的离子浓度比 Table 2 Sulfate concentrations and the corresponding ion ratios on contour radius |
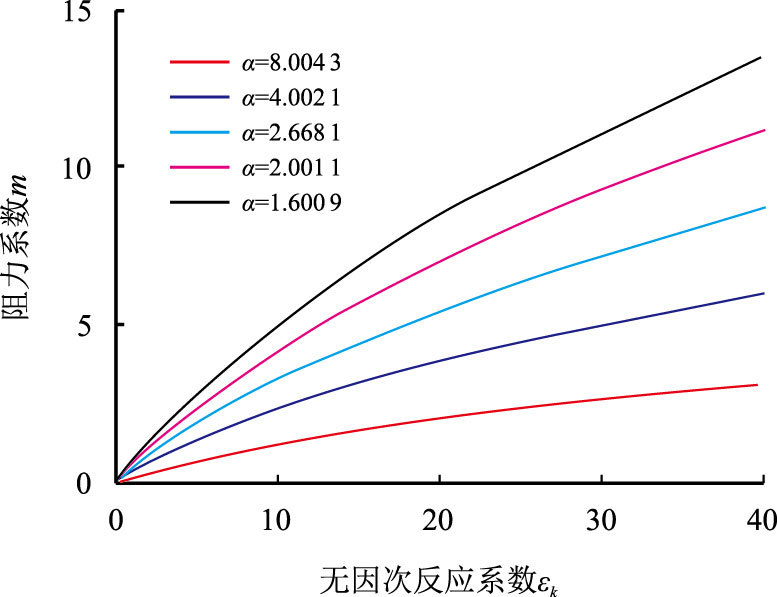 |
| 图2 低硫酸根离子浓度注入水的阻力系数($\varepsilon_{\rm{c}}$=0.1) Fig. 2 Impedance coefficient for low sulfate injection water ($\varepsilon_{\rm{c}}$=0.1) |
由图 2可以看出,反应系数增大,阻力系数上升越慢,反应系数越小,阻力系数增长越快,但是其增长逐渐减缓。进一步分析,当$\varepsilon_{\rm{c}}$=0.1,$\varepsilon_{\rm{k}}$=40,α=2时,阻力系数为13.43。若采用加入阻垢剂来抑制沉淀反应的进行,则当加入阻垢剂使$\varepsilon_{\rm{k}}$减少50%时,阻力系数m减少到8.36;若采用降低注入水中的硫酸根离子浓度来抑制沉淀反应的进行,则当近井地带边界处的硫酸根离子浓度减少50%时,阻力系数m减少到6.01,减幅更大。说明在减少相同百分比的硫酸根离子浓度和$\varepsilon_{\rm{k}}$的情况下,前者对抑制结垢的作用更明显。
图 1图 2对比还可以看出,随着近井地带边界处的硫酸根离子减少(α从0.06增加到1.00以上),阻力系数将大大减少,由原来的102数量级变为101数量级。
4 结论(1) 根据质量守恒方程详细地推导了注水过程中近井地带硫酸钡结垢模型,并修正了控制方程中的二阶项系数。
(2) 岩芯结垢模型与地层结垢模型采用了4阶3步罗巴托法和牛顿迭代法求解,取消了离子浓度比远小于1.00的假设,更适用于油田注水中的地层硫酸钡结垢过程。
(3) 阻力系数随着无因次扩散系数、无因次反应系数的增大而增大,随着离子浓度比的增大而减小;离子浓度比相对于无因次扩散、反应系数来说,对阻力系数的影响更大。
(4) 基于修正后的模型和新的求解方法可以扩展研究各个参数对阻力系数的影响,进而为优选不同阻垢方案提供重要理论依据。
| [1] | BEDRIKOVETSKY P G,LOPES Jr R P,ROSARIO F F, et al. Oilfield scaling-part I:mathematical and laboratory modelling[C]. SPE 81127, 2003. |
| [2] | BEDRIKOVETSKY P G, GLADSTONE P M, LOPES Jr R P, et al. Oilfield scaling-part II:productivity index theory[C]. SPE 81128, 2003. |
| [3] | BYBEE K. Assessing scale risks and uncertainties for subsea marginal-field development[J]. Journal of Petroleum Technology, 2004, 56 (8) : 54 –55. DOI:10.2118/0804-0054-JPT |
| [4] | COLLINS I R, STALKER R, GRAHAM G M. Sulphate removal for barium sulphate scale mitigation a deepwater subsea production system[C]. SPE 87465, 2004. |
| [5] | SIMPSON C, GRAHAM G M, COLLINS I R, et al. Sulphate removal for barium sulphate mitigation-kinetic vs.[C]. SPE 95082, 2005. |
| [6] | GRAHAM G M, MACKAY E J, DYER S J, et al. The challenges for scale control in deepwater production systems-chemical inhibition and placement[C]. SPE 02316, 2002. |
| [7] | JORDAN M M, SJURAETHER K, COLLINS I R, et al. Life cycle management of scale control within subsea fields and its impact on flow assurance gulf of mexico and the north sea basin[C]. SPE 71557, 2001. |
| [8] | MACKAY E J, COLLINS I R, JORDAN M M, et al. PWRI:Scale formation risk assessment and management[C]. SPE 80385, 2003. |
| [9] | GRAHAM G M, COLLINS I R, JOHNSON T J. Technical and economic analysis of the downhole scale risks and uncertainties for subsea and deepwater field developments[C]. SPE 95049, 2005. |
| [10] | JORDAN M M, MACKAY E J. Intergated field development for effective scale control throughout the water cycle in deep water subsea fields[C]. SPE 94052, 2005. |
| [11] | MACKAY E J. Modeling in-situ scale deposition:the impact of reservoir and well geometries and kinetic reaction rates[C]. SPE 81830, 2003. |
| [12] | BEDRIKOVETSKY P G, MACKAY E J, SILVA R M P, et al. Produced water re-injection with seawater treated by sulphate reduction plant:Injectivity decline,analytical model[J]. Journal of Petroleum Science & Engineering, 2009, 68 (1) : 19 –28. |
| [13] | BEDRIKOVETSKY P, SILVA R M, DAHER J S, et al. Well-data-based prediction of productivity decline due to sulphate scaling[J]. Journal of Petroleum Science and Engineering, 2009, 68 (1) : 60 –70. |
| [14] | BEDRIKOVETSKY P, MORAES G, MONTEIRO R, et al. Characterization of sulphate scaling formation damage from laboratory measurements (to predict wellproductivity decline)[C]. SPE 93121, 2005. |
| [15] | GUO J Y, NING J S, ZHANG F P. Chebyshevcollocation method applied to solve ODEs in geophysics singular at the Earth center[J]. Geophysical Research Letters, 2001, 28 (15) : 3027 –3030. DOI:10.1029/2001GL012886 |
| [16] | EDSBERG L, WEDIN P. Numerical tools for parameter estimation in ODE-systems[J]. Optimization Methods and Software, 1995, 6 (3) : 193 –217. DOI:10.1080/10556789508805633 |
 2016, Vol. 38
2016, Vol. 38


