2. 中国石化西南石油工程有限公司井下作业分公司, 四川 德阳 618000;
3. 中国石化石油工程技术研究院, 北京 朝阳 100101;
4. 中国石油塔里木油田分公司库车勘探开发项目经理部, 新疆 库尔勒 841000
2. Downhole Operation Branch, Southwest Petroleum Engineering Company, SINOPEC, Deyang, Sichuan 618000, China;
3. Research Institute of Petroleum Engineering, SINOPEC, Chaoyang, Beijing 100101, China;
4. Kuche Exploration & Development Department, CNPC Tarim Oilfield Company, Korla, Xinjiang 841000, China
岩石可钻性表征一定技术条件下钻头破岩的难易程度,在钻井工程中具有重要应用价值。1951年,Head A L在第三届世界石油大会上,首次提出利用岩石可钻性进行钻头优选[1]。1969年美国德克萨斯州德莱赛工业公司的Morris等利用半径1/8 in.(1 in. = 2.54 cm)牙轮钻头进行岩石可钻性测试:在液压泵作用下,将钻头压入硬质岩石表面,通过压入深度来评价岩石可钻性[2]。此后,国内外学者普遍采用Morris提出的“微钻法”[3-4]进行室内岩石可钻性测试。但是,由于现场取芯数量有限,对于大段地层的岩石可钻性评价则主要依赖于测井解释[5]。测井解释求取岩石可钻性的核心为:利用岩石抗压强度与声波时差之间的回归关系,以及岩石抗压强度与岩石可钻性之间的经验模型,间接求取岩石可钻性[6-7]。由于岩石抗压强度受井底围压影响显著[8],因此获得一个相对准确的井底岩石抗压强度模型,是通过测井资料求取井底岩石可钻性级值的关键。基于空间球对称模型和Drucker-Prager强度准则,在考虑岩石自身力学性质和井底压力环境的基础上,建立了井底岩石可钻性计算模型。利用川西某井须家河组致密砂岩层段室内实验数据和测井资料,评价了钻井液密度对井底岩石可钻性的影响规律,并分析了井底表面径向岩石可钻性的变化规律。
1 井底岩石强度 1.1 井底岩石单元受力分析井底岩石单元受三向地应力和井筒液柱压力共同作用,其中三向地应力包括垂向有效地应力、最大水平主地应力、最小水平主地应力,如图 1所示。
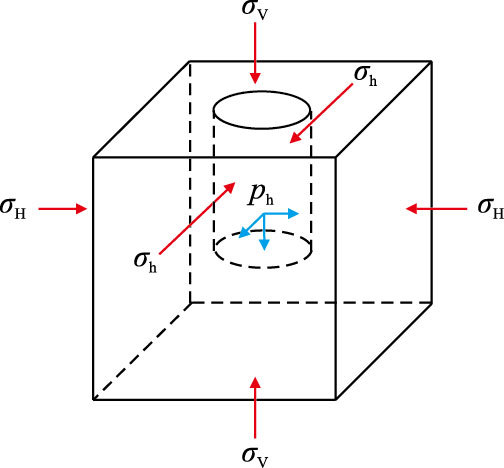 |
| 图1 井底岩石受力示意图 Fig. 1 Stress analysis of bottomhole rock |
钻井过程中,井底岩石应力分布问题属于“端面开挖效应”,目前此类问题尚无解析解[9]。为此,将井底岩石受力模型抽象为内外表面受均布载荷作用的空心圆球[10],在圆球内表面受井筒液柱压力作用,外表面趋于无限大,在无限远处受平均地应力的作用,建立如图 2所示的空间球对称应力模型。
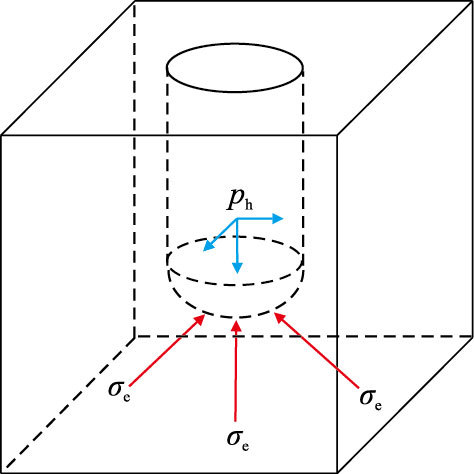 |
| 图2 井底半球应力模型 Fig. 2 Hemisphere stress model of bottom hole |
不考虑地层裂缝、各向非均质性、异常地应力以及地层温度等因素的影响。根据弹性力学理论[11],建立空间球对称问题的基本微分方程:
弹性方程
| $\left\{ \begin{array}{l} {\sigma _{\rm r}}{\rm{ = }}\dfrac{E}{{{\rm{(1 + }}\upsilon {\rm{)(1}} - {\rm{2}}\upsilon {\rm{)}}}}\left[{{\rm{(1}} - \upsilon {\rm{)}}\dfrac{{{\rm{d}}{u_{\rm{r}}}}}{{{\rm{d}}r}}{\rm{ + }}2\upsilon \dfrac{{{u_{\rm r}}}}{r}} \right]\\ {\sigma _\theta }{\rm{ = }}{\sigma _\varphi }{\rm{ = }}\dfrac{E}{{{\rm{(1 + }}\upsilon {\rm{)(1}} - {\rm{2}}\upsilon {\rm{)}}}}\left[{\upsilon \dfrac{{{\rm{d}}{u_{\rm{r}}}}}{{{\rm{d}}r}}{\rm{ + }}\dfrac{{{u_{\rm r}}}}{r}} \right] \end{array} \right.$ | (1) |
平衡方程
| $\dfrac{{E{\rm{(1}} - \upsilon {\rm{)}}}}{{{\rm{(1 + }}\upsilon {\rm{)(1}} - {\rm{2}}\upsilon {\rm{)}}}}\left( {\dfrac{{{{\rm{d}}^{\rm{2}}}{u_{\rm r}}}}{{{\rm{d}}{r^2}}}{\rm{ + }}\dfrac{{{\rm{2d}}{u_{\rm r}}}}{{{\rm{d}}r}} - \dfrac{{{\rm{2}}{u_{\rm r}}}}{{{r^2}}}} \right){\rm{ + }}K{\rm{ = }}0$ | (2) |
井底总应力
| $\left\{ \begin{array}{l} {\sigma _{\rm{r}}} = \dfrac{{{r^3}}}{{{R^3}}}{p_{\rm{h}}}{\rm{ + }}\left( {{\rm{1}} - \dfrac{{{r^3}}}{{{R^3}}}} \right){\sigma _{\rm{e}}}\\ {\sigma _\theta }{\rm{ = }}{\sigma _\varphi } = - \dfrac{{{r^3}}}{{2{R^3}}}{p_{\rm{h}}}{\rm{ + }}\left( {{\rm{1 + }}\dfrac{{{r^3}}}{{2{R^3}}}} \right){\sigma _{\rm{e}}}\\ {\tau _{{\rm{r}}\theta }} = {\tau _{\theta \varphi }} = {\tau _{\varphi {\rm{r}}}} = 0 \end{array} \right.$ | (3) |
无限远处平均地应力${\sigma _{\rm{e}}}$是垂向有效地应力${\sigma _{\rm{v}}}$、最大水平主地应力${\sigma _{\rm{H}}}$、最小水平主地应力${\sigma _{\rm{h}}}$共同作用的结果,${\sigma _{\rm{e}}} = \dfrac{{{\sigma _{\rm{v}}} + {\sigma _{\rm{H}}} + {\sigma _{\rm{h}}}}}{3}$,${\sigma _{\rm{v}}}$可根据修正后的Terzaghi有效应力原理计算[12],${\sigma _{\rm{H}}}$和${\sigma _{\rm{h}}}$可根据组合弹簧构造运动模型推导出的分层地应力公式计算[13]。${{\sigma _{\rm{v}}} {,} {\sigma _{\rm{H}}} {,} {\sigma _{\rm{h}}}}$的计算公式分别为
| ${\sigma _{\rm v}} = {\sigma _ \bot } - \alpha {p_{\rm{p}}}$ | (4) |
| ${\sigma _{\rm{H}}} = \dfrac{{{\xi _1}E + 2\upsilon \left( {{\sigma _{\rm v}} - \alpha {p_{\rm{p}}}} \right)}}{{2(1 - \upsilon )}} + \dfrac{{{\xi _2}E}}{{2(1 + \upsilon )}} + \alpha {p_{\rm{p}}}$ | (5) |
| ${\sigma _{\rm{h}}} = \dfrac{{{\xi _1}E + 2\upsilon \left( {{\sigma _{\rm v}} - \alpha {p_{\rm{p}}}} \right)}}{{2(1 - \upsilon )}} - \dfrac{{{\xi _2}E}}{{2(1 + \upsilon )}} + \alpha {p_{\rm{p}}}$ | (6) |
岩石所处应力状态对岩石强度具有显著影响,只有得出实际应力环境,才能对实际岩石强度作出准确的评估。根据岩石强度理论,岩石强度需要考虑最小主应力和中间主应力的影响。在空间球对称模型中,岩石单元应力状态与方位角和倾角无关,且岩石单元不受切应力作用。根据式(3),若${\sigma _{\rm{r}}} > {\sigma _\theta }$(${p_{\rm{h}}} > {\sigma _{\rm{e}}}$),则
| ${\sigma _2} = {\sigma _3} = - \dfrac{{{r^3}}}{{2{R^3}}}{p_{\rm{h}}}{\rm{ + }}\left( {{\rm{1 + }}\dfrac{{{r^3}}}{{2{R^3}}}} \right){\sigma _{\rm{e}}}$ | (7) |
若${\sigma _{\rm{r}}} < {\sigma _\theta }$(${p_{\rm{h}}} < {\sigma _{\rm{e}}}$),则
| ${\sigma _2} = {\sigma _3} = \dfrac{{{r^3}}}{{{R^3}}}{p_{\rm{h}}}{\rm{ + }}\left( {{\rm{1 - }}\dfrac{{{r^3}}}{{2{R^3}}}} \right){\sigma _{\rm{e}}}$ | (8) |
Drucker-Prager强度准则考虑了中间主应力和平均应力对岩石强度的影响。同时,Drucker-Prager强度准则在主应力空间的屈服面为光滑圆锥面,在 平面上为圆形,不存在顶尖处的数学计算问题[14, 15]。因此,相比油气井工程领域常用的Mohr-Coulomb强度准则而言,采用Drucker-Prager强度准则更适合于求取井底空间球对称模型中的岩石强度。Drucker-Prager强度准则表示为
| $\left\{ \begin{array}{l} {\alpha _1}{I_1} + \sqrt {{J_2}} \!=\! {K_{\rm f}}\\ {{{I}}_1} \!=\! \dfrac{1}{3}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)\\ {J_2} \!=\! \dfrac{1}{6}\left[{{{\left( {{\sigma _1}\! - \!{\sigma _2}} \right)}^2} \!+\! {{\left( {{\sigma _2} \!-\! {\sigma _3}} \right)}^2} \!+\! {{\left( {{\sigma _3} \!-\! {\sigma _1}} \right)}^2}} \right] \end{array} \right.$ | (9) |
其中:${\alpha _1}{\rm{ = }}\dfrac{{\sqrt 3 \sin {\varphi _{\rm{s}}}}}{{3\sqrt {3 + {{\sin }^2}{\varphi _{\rm s}}} }}$;${K_{\rm{f}}}{\rm{ = }}\dfrac{{\sqrt 3 \cos {\varphi _{\rm{s}}}}}{{3\sqrt {3 + {{\sin }^2}{\varphi _{\rm{s}}}} }}C$。
联立式(7)~式(9),即可获得井底半球应力模型下的岩石强度
| ${\sigma _1} = \left\{ \begin{array}{l} \dfrac{{{\rm{2}}\sqrt 3 {K_{\rm{f}}}{R^3}{\rm{ + }}\left( {{\rm{1 - 2}}\sqrt 3 } \right)\left[ {\left( {{r^3}{\rm{ + }}2{R^3}} \right){\sigma _{\rm{e}}} - {r^3}{p_{\rm{h}}}} \right]}}{{\left( {{\rm{2}}\sqrt 3 {\alpha _1}{\rm{ + 2}}} \right){R^3}}}\mbox{,} {\kern 35pt}\left( {{p_{\rm{h}}} > {\sigma _{\rm{e}}}} \right)\\[8pt] \dfrac{{\sqrt 3 {K_{\rm{f}}}{R^3}{\rm{ + }}\left( {{\rm{1 - 2}}\sqrt 3 } \right)\left[ {\left( {{R^3} - {r^3}} \right){\sigma _{\rm{e}}} + {r^3}{p_{\rm{h}}}} \right]}}{{\left[ {\sqrt 3 {\alpha _1}{\rm{ + 1}}} \right]{R^3}}}\mbox{,} {\kern 40pt} \left( {{p_{\rm{h}}} < {\sigma _{\rm{e}}}} \right) \end{array} \right.$ | (10) |
根据岩石可钻性测试标准[16],采用全自动岩石可钻性测试仪进行实验。利用牙轮微型钻头,对川西地区须家河组致密砂岩进行室内岩石可钻性测试,结果如图 3、表 1所示。同时,利用岩石力学试样机测试岩样单轴抗压强度,测试结果见表 2。
 |
| 图3 川西地区须家河组致密砂岩岩石可钻性测试结果 Fig. 3 Result of drillability test of the sandstone reservoir in Xujiahe Group |
| 表1 川西地区须家河组致密砂岩岩石可钻性级值 Table 1 Drillability of the sandstone reservoir in Xujiahe Group |
| 表2 须家河组致密砂岩岩石单轴抗压强度 Table 2 Uniaxial compressive strength of the sandstone reservoir in Xujiahe Group |
根据李士斌等[17]对岩石可钻性的研究结论,采用线性关系对岩石抗压强度和可钻性级值进行拟合,得到相关系数为0.940~9的关系表达式
| ${K_{\rm{d}}} = 0.0137\sigma + 4.7012$ |
假设由岩石单轴抗压强度与可钻性之间确定的关系模型,可以反映井底围压条件下岩石抗压强度与可钻性之间的关系特征。因此,将式(10)代入式(11),即可得到井底岩石可钻性计算模型
当${{p_{\rm{h}}} > {\sigma _{\rm{e}}}}$时
| $K_{\rm{d}}=\dfrac{{0.0137\left( {{\rm{1 - 2}}\sqrt 3 } \right)\left[ {\left( {{r^3}{\rm{ + }}2{R^3}} \right){\sigma _{\rm{e}}} - {r^3}{p_{\rm{h}}}} \right]}}{{\left( {{\rm{2}}\sqrt 3 {\alpha _1}{\rm{ + 2}}} \right){R^3}}} + \\[6pt]{\kern 40pt}\dfrac{{{\rm{0}}{\rm{.0274}}\sqrt 3 {K_{\rm{f}}}}}{{{\rm{2}}\sqrt 3 {\alpha _1}{\rm{ + 2}}}}+4.7012$ | (12) |
当${{p_{\rm{h}}} < {\sigma _{\rm{e}}}}$时
| $K_{\rm{d}}=\dfrac{{0.0137\left( {{\rm{1 - 2}}\sqrt 3 } \right)\left[ {\left( {{R^3} - {r^3}} \right){\sigma _{\rm{e}}} + {r^3}{p_{\rm{h}}}} \right]}}{{\left( {\sqrt 3 {\alpha _1}{\rm{ + 1}}} \right){R^3}}} + \\[6pt]{\kern 40pt}\dfrac{{0.0137\sqrt 3 {K_{\rm{f}}}}}{{\sqrt 3 {\alpha _1}{\rm{ + 1}}}}{\rm{ + }}4.7012$ | (13) |
川西某井须家河组致密砂岩地层,基本参数如下:井深2 077.25~2 280.00 m;井眼直径0.216 m;井斜角为0;地层平均密度2.470 g/cm3;泥质含量参数取2;地层平均孔隙压力换算成的当量密度取1.017 g/cm3。依据文献[18]中川西须家河组致密砂层构造应力系数,对比式(5)和式(6),折算得到最大水平主地应力方向构造应力系数${\xi _1}{\rm{ = 4}}{\rm{.469}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}$,最小水平主地应力方向构造应力系数${\xi _2}{\rm{ = 1}}{\rm{.15}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}$。
计算过程中,利用式(12)、式(13)计算井底岩石可钻性级值,其中计算所涉及的过程参数均利用文献[19]中的测井解释公式进行求取。
3.1 井底表面径向岩石可钻性在油气井工程中,井底表面径向的岩石可钻性(这里以可钻性级值表示),对于钻头优化设计具有重要的工程应用价值。在上述基本参数的基础上,钻井液密度值取1.0 g/cm3,分析井深2 077.25 m处井底表面($R = 0.216$ m)径向岩石可钻性,其中$r/R$取值区间为[0,1.0],步长为0.1,$r/R=0$代表井底中心,$r/R = 1.0$代表井底与井壁交界处,结果如图 4所示。
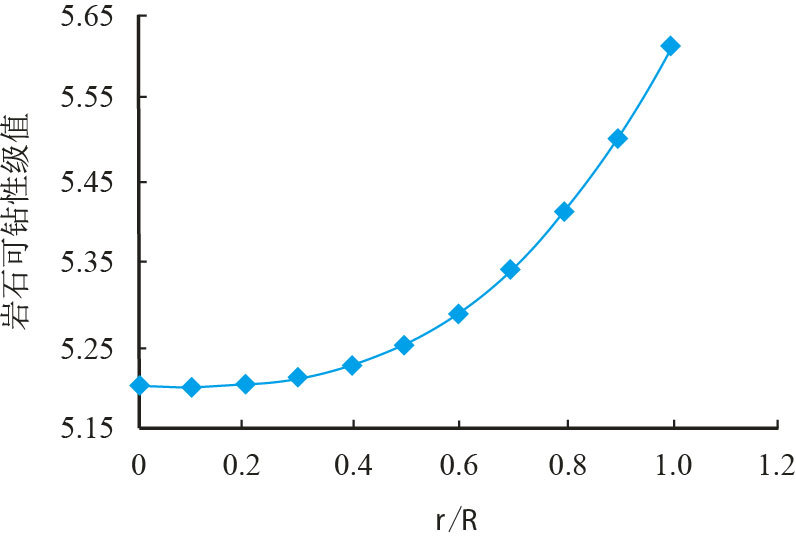 |
| 图4 井底表面径向不同距离处岩石可钻性 Fig. 4 Drillability at different radial distances on the bottom surface |
由图 4可见,随着$r/R$(井底径向距离)的增加,井底表面岩石可钻性增大。井壁与井底交界处的“应力集中”现象,是造成井底应力场分布不均,进而影响井底表面岩石可钻性的主要原因。因此,在钻头设计过程中,应当优化钻头边缘齿的设计,以保证钻头破岩过程均匀推进,提高钻头使用寿命和井身质量。
3.2 钻井液密度对井底岩石可钻性的影响在油气井工程中,井筒延伸方向的岩石可钻性,对于钻头序列优选具有重要的工程应用价值。在上述基本参数的基础上,钻井液密度值分别取0.8,1.0,1.2 g/cm3,分析钻井液密度对井底表面中心($R = 0.216$ m,$r = 0$)处岩石可钻性的影响,结果如图 5所示。
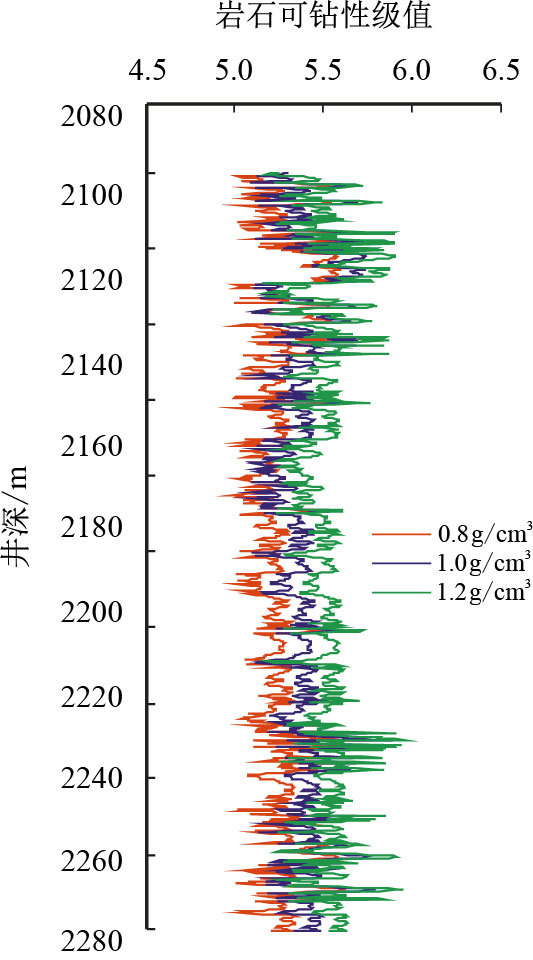 |
| 图5 不同钻井液密度下的岩石可钻性 Fig. 5 Drillability of different drilling fluid densities |
由图 5可见,随着井深增加,井底岩石可钻性级值增大,即井深越深越不利于钻头破岩,理论计算结果与钻井实践相符合;同时,随着钻井液密度升高,井底岩石可钻性级值增大。井筒液柱压力增大,引起井底岩石所处应力状态发生改变,导致岩石强度增加,是造成这一现象的主要原因之一。钻井液密度对井筒延伸方向岩石可钻性的影响规律,可以作为现场钻井过程中实施“降低钻井液密度,提高钻井机械钻速”的依据,并可以对降低钻井液密度所产生的提速效果进行预测和评价。
4 结论(1) 基于空间球对称坐标系建立的井底岩石可钻性模型,能够较好地反映井底岩石可钻性级值的分布规律。
(2) 对于深井钻井而言,井筒液柱压力是影响井底岩石可钻性的主要因素,且井底所受液柱压力越大,钻头破岩越困难。因此,降低钻井液密度仍然是深井提速的有效途径之一。
(3) 井底表面径向岩石可钻性随着径向距离的增加而增大。因此,在钻头设计过程中应该优化钻头边缘齿设计,以保证钻头破岩均匀推进,提高钻头使用寿命和井身质量。
符号说明
${\sigma _{\rm{v}}}$—垂向有效地应力,MPa;
${\sigma _{\rm{H}}}$—最大水平主地应力,MPa;
${\sigma _{\rm{h}}}$—最小水平主地应力,MPa;
${\sigma _{\rm{e}}}$—无限远处平均地应力,MPa;
${\sigma _{\rm{r}}}$—井底岩石单元所受径向应力,MPa;
${\sigma _{\rm{\theta}}}$—井底岩石单元所受切向应力,MPa;
${\sigma _{\rm{\varphi}}}$—井底岩石单元所受周向应力,MPa;
${\tau _{{\rm{r}}\theta }}{,}{\tau _{\theta \varphi }}{,}{\tau _{\varphi {\rm{r}}}}$—井底岩石单元3个方向的剪应力,MPa;
E—地层岩石弹性模量,MPa;
$\upsilon$—地层岩石泊松比;
${u _{\rm{r}}}$—井底岩石单元径向位移分量,m;
K—井底岩石单元所受体积力,MPa;
${p _{\rm{h}}}$—井底岩石单元所受液柱压力,MPa;
${r _{\rm{}}}$—井眼半径,m;
${R _{\rm{}}}$—井眼周围地层半径,m;
${\sigma _ \bot }$—上覆岩层压力,MPa;
${p _{\rm{p}}}$—地层孔隙压力,MPa;
$\xi _1$,$\xi_ 2$—最大、最小水平主地应力系数,无因次;
$\alpha$—有效应力系数,无因次;
${\sigma _{\rm{2}}}$—中间主应力,MPa;
${\sigma _{\rm{3}}}$—最小主应力,MPa;
${\sigma _{\rm{1}}}$—最大主应力,MPa;
I1—应力张量第一不变量,MPa;
J2—第二应力偏量不变量,MPa2;
$\varphi_{\rm s}$—岩石内聚力,MPa;
C—岩石内摩擦角,rad;
$K_{\rm d}$—牙轮微型钻头对应的可钻性级值,无因次;
$\sigma $—岩石单轴抗压强度,MPa。
| [1] | HEAD A L. A drillability classification of geological formation[C]//The 3rd World Petroleum Congress, 1951. |
| [2] | MORRIS, RICHARD I. Rock drillability related to a roller cone bit[R]. Drilling and Rock Mechanics Symposium, Texas, 1969. |
| [3] |
邹德永, 尹宏锦. PDC钻头钻进的岩石可钻性研究[J].
石油大学学报(自然科学版), 1993, 17 (1) : 31 –35.
ZOU Deyong, YIN Hongjin. Study on rock-drillability for PDC bit drilling[J]. Journal of the University of Petroleum, 1993, 17 (1) : 31 –35. |
| [4] | Gstalder S, Raynal J. Measurement of some mechanical properties of rocks and their relationship to rock drillability[J]. Journal of Petroleum Technology, 1966, 18 (8) : 991 –996. DOI:10.2118/1463-PA |
| [5] |
刘向君, 宴建军, 罗平亚, 等. 利用测井资料评价岩石可钻性研究[J].
天然气工业, 2005, 25 (7) : 69 –71.
LIU Xiangjun, YAN Jianjun, LUO Pingya, et al. Evaluation on rock drillability by well logging data[J]. Natural Gas Industry, 2005, 25 (7) : 69 –71. |
| [6] | ANDREWS R J, HARELAND G, NYGAARD R, et al. Methods of using logs to quantify drillability[C]. Rocky Mountain Oil & Gas Technology Symposium. Society of Petroleum Engineers, 2007. |
| [7] |
杨谋, 孟英峰, 李皋, 等. 不同钻井方式下的井底岩石可钻性研究[J].
石油钻探技术, 2010, 38 (2) : 19 –22.
YANG Mou, MENG Yingfeng, LI Gao, et al. Investigation of rock drillability under different penetrating method[J]. Petroleum Drilling Techniques, 2010, 38 (2) : 19 –22. |
| [8] |
邢福东, 朱珍德, 刘汉龙, 等. 高围压高水压作用下脆性岩石强度变形特性试验研究[J].
河海大学学报(自然科学版), 2004, 32 (2) : 184 –187.
XING Fudong, ZHU Zhende, LIU Hanlong, et al. Experimental study on strength and deformation characteristics of brittle rocks under high confining pressure and hydraulic pressure[J]. Journal of Hehai University(Natural Sciences), 2004, 32 (2) : 184 –187. |
| [9] |
常德玉, 李根生, 沈忠厚, 等. 考虑三向地应力差时不同钻井条件下井底应力场研究[J].
岩土力学, 2011, 32 (5) : 1146 –1152.
CHANG Deyu, LI Gensheng, SHEN Zhonghou, et al. Study of bottom-hole stress field with differential pressure of 3D in-situ stress under different drilling conditions[J]. Rock and Soil Mechanics, 2011, 32 (5) : 1146 –1152. |
| [10] |
仉洪云, 高德利, 郭柏云. 热膨胀系数对气体钻井井底岩石应力场的影响[J].
西南石油大学学报(自然科学版), 2012, 34 (4) : 88 –93.
ZHANG Hongyun, GAO Deli, GUO Boyun. Influence of the Coefficient of Thermal Expansion on the Stress of Bottom Hole Rock in Gas Drilling[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2012, 34 (4) : 88 –93. |
| [11] |
徐芝纶.
弹性力学[M]. 北京: 高等教育出版社, 2006 .
XU Zhilun. Elastic Mechanics[M]. Beijing: Higher Education Press, 2006 . |
| [12] |
李忠平, 周文, 谢润成, 等. Biot系数非线性解释初探及其在井壁稳定性分析中的应用[J].
石油钻采工艺, 2012, 34 (1) : 39 –42.
LI Zhongping, ZHOU Wen, XIE Runcheng, et al. Preliminary study on non-liner interpretation of biot coefficient of rock and its application on the analysis of wellbore stability[J]. Oil Drilling & Production Technology, 2012, 34 (1) : 39 –42. |
| [13] |
邓金根, 程远方, 陈勉, 等.
井壁稳定预测技术[M]. 北京: 石油工业出版社, 2008 .
DENG Jin'gen, CHENG Yuanfang, CHEN Mian, et al. The borehole wall stability prediction technology[M]. Beijing: Petroleum Industry Press, 2008 . |
| [14] |
赵尚毅, 郑颖人, 刘明维, 等. 基于Drucker-Prager准则的边坡安全系数定义及其转换[J].
岩石力学与工程学报, 2006, 25 (S1) : 2730 –2734.
ZHAO Shangyi, ZHENG Yingren, LIU Mingwei, et al. Definition and transformation of slope safety factor based on Drucker-Prager Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25 (S1) : 2730 –2734. |
| [15] |
陈勉, 金衍, 张广清.
石油工程岩石力学[M]. 北京: 科学出版社, 2008 .
CHEN Mian, JIN Yan, ZHANG Guangqing. Petroleum Engineering Rock Mechanics[M]. Beijing: Science Press, 2008 . |
| [16] |
YANG Defeng, FAN Ji'an, GAO Xuezhi. SY/T5426-2000 Rock drillability measurement and classification method[S]. Beijing:National Petroleum and Chemical Industry, 2000.
杨德凤,樊冀安,高学之. SY/T5426-2000岩石可钻性测定及分级方法[S]. 北京:国家石油与化学工业局, 2000. |
| [17] |
李士斌, 阎铁, 韩辉, 等. 模拟井底应力条件下的岩石可钻性实验研究[J].
天然气工业, 2003, 23 (2) : 64 –66.
LI Shibin, YAN Tie, HAN Hui, et al. Drillability test study under modeling conditions of bottom hole stress[J]. Natural Gas Industry, 2003, 23 (2) : 64 –66. |
| [18] |
MA Faming. Theory and technology research of Xujiahe deep fractured gas reservoir fracturing in west Sichuan[D]. Chengdu:Southwest Petroleum University, 2009.
马发明. 川西须家河深层裂缝性气藏压裂理论与应用技术研究[D]. 成都:西南石油大学, 2009. |
| [19] |
刘向君, 刘堂晏, 刘诗琼.
测井原理及工程应用[M]. 北京: 石油工业出版社, 2010 .
LIU Xiangjun, LIU Tangyan, LIU Shiqiong. Logging principle and engineering application[M]. Beijing: Petroleum Industry Press, 2010 . |
 2016, Vol. 38
2016, Vol. 38


