2. 低渗透油气田勘探开发国家工程实验室, 陕西 西安 710018
2. State Project Laboratory of Low permeability Oil and Gas Exploration and Development, Xi'an, Shaanxi 710018, China
安塞油田是长庆油田的主力油田之一,自20世纪80年代全面投入开发以来,经过30 a的开发,已经进入了高含水期,严重阻碍了油田的快速开发。长庆油田分公司以加密井钻井开发试验为先导,开展了老油田加密井安全钻井技术试验,以达到有效开采剩余油气资源,提高采收率的目的。加密区的井网形式为300 m×300 m正方形反九点井网,钻井方式采用丛式定向井组,井场井数为3~5口。加密井方案均是在原有井场实施,这就使得井距由原来的300 m缩短至240~260 m,排距缩短至160~190 m。这些变化加上加密区多年的注水开发造成的地层压力系统极其紊乱,导致在加密调整试验区钻井过程中可能会遇到一系列的复杂钻井问题,其中最突出的就是钻井过程中的井控问题。而由于加密地区地层压力系统的紊乱,造成了有时异常高压和异常低压在地层平面及剖面方向上并存,如果在这样的复杂地层和压力系统下钻加密井,就有可能发生漏、喷、塌、卡等井下复杂情况,严重影响加密井钻井施工顺利进行,给油田开发带来巨大损失。
针对这些问题,开展安塞油田加密井试验区地层压力预测研究,以建立准确预测加密井地层压力及其动态变化规律的措施,达到减少或减轻相关钻井事故,提高钻井速度、降低钻井成本的目的。
1 裂缝性地层加密井压力预测 1.1 非均质地层压力预测数学模型地层的非均质性会导致地层在不同区域表现出完全不同的地质特征,进而致使压力、渗流速度和含油饱和度等呈现非连续性分布。但是,如果将地层分割成很多个小的微元体,就可以将非均质地层看成均质地层来进行处理,微元体思想就是建立非均质地层压力预测数学模型的基础[1-3]。从地层中任取一个微元体作为研究对象,如图 1所示。
由质量守恒原理,假设有流体在x方向上流经地层单元,那么,对于任一瞬时,流入质量流量 - 流出质量流量 = 累计质量速率,有
| $({\rho _x}{v_x}\Delta y\Delta z) - ({\rho _{x + \Delta x}}{v_{x + \Delta x}}\Delta y\Delta z) =\\ {\kern42pt}(\Delta x\Delta y\Delta z)\phi \dfrac{{({\rho _{t + \Delta t}} - {\rho _t})}}{{\Delta t}}$ | (1) |
式中:
${\rho _x}$—x处的密度,kg/m3;
${v _x}$—x处的速度,m/s;
$\Delta x{,}\Delta y{,}\Delta z$—微元体的长、宽、高,m;
${\rho _{x+\Delta x}}$—$x+\Delta x$处的密度,kg/m3;
${v _{x+\Delta x}}$—$x+\Delta x$处的速度,m/s;
φ—孔隙度,%;
${\rho _{t}}$—t时刻微元体内流体的密度,kg/m3;
${\rho _{t+\Delta t}}$—$t+\Delta t$时刻微元体内流体的密度,kg/m3;
t—时间,s。
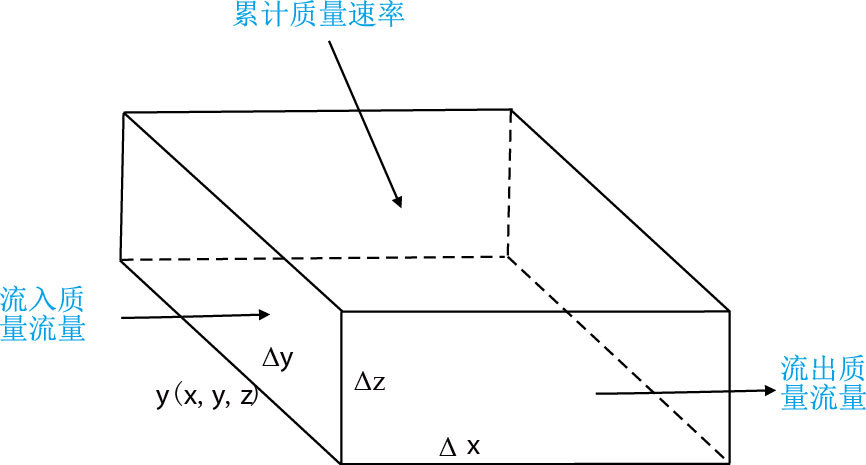 |
| 图1 微元体质量流动示意图 Fig. 1 Schematic diagram of micro body mass flow |
由式(1),忽略重力作用,不考虑岩石的压缩性,假设地层流体渗流符合达西定律且微可压缩,结合渗流方程,可以得到非均质地层二维油水两相流压力预测数学模型
| $ \dfrac{\partial }{{\partial x}}\left( {\dfrac{{{K_x}{K_{{\rm{ro}}}}}}{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}\dfrac{{\partial p}}{{\partial x}}} \right) \!+\! \dfrac{\partial }{{\partial y}}\left( {\dfrac{{{K_y}{K_{{\rm{ro}}}}}}{{{B_{\rm{o}}}{\mu _{\rm{o}}}}}\dfrac{{\partial p}}{{\partial y}}} \right) \!+\! {q_{\rm{v}}} \!=\! \dfrac{{\phi C}}{{{B_{\rm{o}}}}}\dfrac{{\partial p}}{{\partial t}}$ | (2) |
| $ \dfrac{\partial }{{\partial x}}\left( {\dfrac{{{K_x}{K_{{\rm{rw}}}}}}{{{B_{\rm{w}}}{\mu _{\rm{w}}}}}\dfrac{{\partial p}}{{\partial x}}} \right) \!+\! \dfrac{\partial }{{\partial y}}\left( {\dfrac{{{K_y}{K_{{\rm{rw}}}}}}{{{B_{\rm{w}}}{\mu _{\rm{w}}}}}\dfrac{{\partial p}}{{\partial y}}} \right) \!+\! {q_{\rm{v}}} \!=\! \dfrac{{\phi C}}{{{B_{\rm{w}}}}}\dfrac{{\partial p}}{{\partial t}} $ | (3) |
式中:
$K_x$—x方向渗透率,mD;
${K_{{\rm{ro}}}}$—油相对渗透率,%;
${B_{{\rm{o}}}}$—油相体积系数,m3/m3;
${\mu_{{\rm{o}}}}$—油相黏度,mPa·s;
p—压力,MPa;
$K_y$—y方向渗透率,mD;
$q_{\rm v}$—单位长度下的流量,m2/s;
C—压缩系数,MPa-1;
${K_{{\rm{rw}}}}$—水相对渗透率,%;
${B_{{\rm{w}}}}$—水相体积系数,m3/m3;
${\mu_{{\rm{w}}}}$—水相黏度,mPa·s。
对于多井生产的地层系统,需要用到压力和势的叠加原理来进行压力分布的叠加计算,以得到复杂生产系统的压力分布。
1.2 复杂裂缝地层加密井压力预测数学模型(1) 复杂裂缝地层渗透率计算方法
裂缝性地层的地层压力分布规律以及动态变化特征主要受裂缝地层渗透率的各向异性影响,在对裂缝地层特性进行研究之前,需要首先对复杂裂缝地层渗透率的表达方式进行研究与讨论。
实际情况下,裂缝地层中构造应力的分布对裂缝的分布规律起到主要的控制作用。虽然裂缝性地层中裂缝的发育看起来错综复杂,但通过研究构造应力场的规律仍可发现裂缝发育所存在的规律,这种规律可以理解为发育出的裂缝有规律的相互交叉形成了一个网络系统[4-8],可利用裂缝网络的这一特性来研究其渗透特性。
非均质性和各向异性是裂缝地层固有的属性。裂缝地层中不同空间点的渗透率差异就是渗透率非均质性的体现,裂缝地层中同一点但不同方向上的渗透率所存在的差异为渗透率各向异性的体现。因此,地层中裂缝的发育导致了渗透率特征的变化,这一变化主要体现在两个方面:一是导致地层渗透率产生非均质性;二是使地层的渗透率表现出各向异性的特点[9-12]。为了更好地描述裂缝性地层的渗透率,引入渗透率张量的概念。忽略岩石基质渗流,将错综复杂的裂缝网简化,将其视为多组平行的裂缝且组与组交叉呈网络状,并假设这些裂缝组构成了裂缝性地层的主要流动通道,且各组间的流动不受彼此影响。通过这种假设,地层中的裂缝网格被简化为数个仅有唯一方向的裂缝组,这种虚构介质更加便于对裂缝性地层渗透率特性的研究,其各裂缝组的流动叠加就等价于实际地层的流动特性[13-15]。实际裂缝性地层的渗透率张量为
| $\begin{align} & \mathbf{K}=\sum\limits_{m=1}^{M}{\frac{{{\left( {{S}^{\left( m \right)}} \right)}^{3}}}{12{{b}^{\left( m \right)}}}} \\ & \left[ \begin{matrix} {{\left( \mathbf{n}_{2}^{\left( m \right)} \right)}^{2}}+{{\left( \mathbf{n}_{3}^{\left( m \right)} \right)}^{2}} & -\mathbf{n}_{1}^{\left( m \right)}\mathbf{n}_{2}^{\left( m \right)} & -\mathbf{n}_{3}^{\left( m \right)}\mathbf{n}_{1}^{\left( m \right)} \\ -\mathbf{n}_{1}^{\left( m \right)}\mathbf{n}_{2}^{\left( m \right)} & {{\left( \mathbf{n}_{3}^{\left( m \right)} \right)}^{2}}+{{\left( \mathbf{n}_{1}^{\left( m \right)} \right)}^{2}} & -\mathbf{n}_{2}^{\left( m \right)}\mathbf{n}_{3}^{\left( m \right)} \\ -\mathbf{n}_{3}^{\left( m \right)}\mathbf{n}_{1}^{\left( m \right)} & -\mathbf{n}_{2}^{\left( m \right)}\mathbf{n}_{3}^{\left( m \right)} & {{\left( \mathbf{n}_{1}^{\left( m \right)} \right)}^{2}}+{{\left( \mathbf{n}_{2}^{\left( m \right)} \right)}^{2}} \\ \end{matrix} \right] \\ \end{align}$ | (4) |
| ${\kern 42pt} \left| {\bf{K}} \right| = \sum\limits_{m = 1}^M {\dfrac{{{{\left ({S^{\left (m\right )}}\right )}^3}}}{{12{b^{\left (m\right )}}}}} \left[{\begin{array}{*{20}{c}} {1 - {{\left (a_x^{\left (m\right )}\right )}^2}} & { - a_x^{\left (m\right )}a_y^{\left (m\right )}} & { - a_z^{\left (m\right )}a_x^{\left (m\right )}}\\ { - a_x^{\left (m\right )}a_y^{\left (m\right )}} & {1 - {{\left (a_y^{\left (m\right )}\right )}^2}} & { - a_y^{\left (m\right )}a_z^{\left (m\right )}}\\ { - a_z^{\left (m\right )}a_x^{\left (m\right )}} & { - a_y^{\left (m\right )}a_z^{\left (m\right )}} & {1 - {{\left (a_z^{\left (m\right )}\right )}^2}} \end{array}} \right]$ | (5) |
其中:
$a_x^{\left (m\right )}=\sin{\alpha^{(m)}}\cos{\beta^{(m)}}$;
$a_y^{\left (m\right )}=\sin{\alpha^{(m)}}\sin{\beta^{(m)}}$;
$a_z^{\left (m\right )}=\cos{\alpha^{(m)}}$;
M—裂缝组数,由裂缝的发育程度所决定;
${b^{\left (m\right )}}$—第m组裂缝的平均间距,m;
${S^{\left (m\right )}}$—第m组裂缝的平均宽度,m;
${{\bf{n}}} _1^{\left (m\right )}$,${{\bf{n}}} _2^{\left (m\right )}$,${{\bf{n}}} _3^{\left (m\right )}$—第m组裂缝面法向量${{\bf{n}}}^{(m)}$沿三维空间坐标方向的3个分量;
$\alpha^{\left (m\right )}$—m组裂缝的倾角,(°),0° $\leqslant\alpha^{\left (m\right )} \leqslant$ 90° ;
$\beta^{\left (m\right )}$—m组裂缝的倾向(用方位角表示),(°),0° $\leqslant\alpha^{\left (m\right )} \leqslant$ 360° 。
(2) 复杂裂缝地层压力分布计算
假设无限大水平各向异性地层中,有一口以产量Q稳产的生产井,井底压力为$p_{\rm w}$,井底有一长为2l的裂缝,它与各向异性渗透率最大主轴方向(即x轴方向)夹角为$\alpha$,如图 2所示。
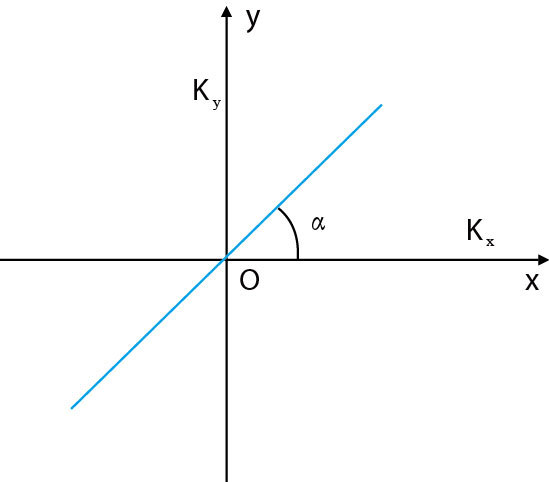 |
| 图2 各向异性地层中裂缝方位 Fig. 2 Fracture azimuth anisotropic formation |
各向异性地层中有限长裂缝影响下地层压力近似计算公式为
| $p = {p_{\rm{w}}} + \dfrac{{\mu Q}}{{2\pi Kh}}\ln \dfrac{{2\sqrt {{x^2} + {c^2}{y^2}} }}{{l\sqrt {{{\cos }^2}\alpha + {c^2}{{\sin }^2}\alpha } }}$ | (6) |
式中:
${p_{\rm{w}}}$—井底压力,MPa;
$\mu$—黏度,mPa·s;
Q—产量,m3/d;
K—渗透率,mD;
h—产层厚度,m;
l—裂缝半长,m;
$\alpha$—方位角,(°);
c—系数,$c=\left( K_x/K_y \right)^{0.5}$。
从式(6)可以看出,地层中某一点压力除了与地层特征有关之外,还与井的产量(注入量)的大小、位置关系、裂缝半长、方位角及裂缝开度和叉分比控制的地层渗透率K有直接关系。适用条件为$r=\sqrt {{x^2} + {y^2}} \gg l$。
式(6)是地层中只存在一条裂缝和一口井生产的情况下的压力分布计算公式。对于复杂裂缝地层,首先,需要根据式(5)计算出地层的渗透系数张量;然后,再用式(6)进行地层压力计算。对于多井生产的裂缝地层系统,还需要根据叠加原理进行计算才能得到加密井的地层压力。
2 安塞地区加密井地层压力预测安塞油田王窑加密试验区位于王窑中西部,开发时间较长,经历了探井试采、井组划分、先导性及工业化开发试验,在1991年安塞油田全面投入注水开发,动用Ⅲ类地质储量2 951×104~t,含油面积为43.5 km2。至2009年12月,试验区共有采油井38口,开井37口,综合含水58.9%,地质储量采出程度11.8%,储层平均深度为1 400 m。共有注水井10口,开井9口日平均注水180 m3,单井日注水量20 m3,月注采比1.1,累计注采比1.1。
在王窑中西部选择开发时间较长、钻井井网较完善的王19-03—王22-07区域,包括8个井组。该井网多数为1996—1998年投产投注;原井网为300 m×300 m的正方形反九点井网,井网密度为11.9口/km2,井排方向近东西向。
选择资料比较全的井组对加密井地层压力进行预测。该井组共有王19-04、王19-05、王20-03、王20-04和王20-042共5口井。其中王19-04是转注油井,王19-05和王19-30是生产井,王20-04是注水井,王20-042则是将要进行地层压力预测的目标井。
2.1 基础数据井组地层基础数据如表 1所示,对目标加密井地层压力有影响的相关井位数据以及目标井(王20-042)的井位数据如表 2所示。
| 表1 井组地层基础数据 Table 1 Formation data of well group |
| 表2 邻井相关数据 Table 2 Adjacent well data |
对受加密井附近4口井(王19-04、王19-05、王20-03和王20-04)影响的地层压力和渗流速度进行计算,确定目标加密井(王20-042)的地层压力为14.574 MPa,而实际王20-042的地层压力为14.130 MPa,地层压力系数为1.14,该系数在正常地层压力0.8~1.2内,预测结果经过对比误差为3.17%。
所选研究井组有3口生产井1口注水井,而3口生产井的产量为44.06 m3/d大于注水井的注入量20 m3/d,模拟预测点的压力为14.353 MPa,随着时间的增加,压力是降低的,但其地层压力系数为1.12,仍在正常地层压力的范围之内。若出现异常高压或者异常低压,则可调整邻近4口井的生产或注入量,以对地层压力进行定量控制,从而实现快速安全钻井。按照相同的思路和步骤,对安塞地区其他几口加密井的地层压力进行了预测,与实测压力对比如下:王26-03井预测和实测结果分别为14.33,13.74 MPa,预测误差4.2%; 王加21-1164井预测和实测结果分别为15.60,15.12 MPa,预测误差3.2%; 王加25-054井预测和实测结果分别为15.36,14.45 MPa,预测误差6.2%; 王加27-043井预测和实测结果分别为16.73,16.04 MPa,预测误差4.3%。
3 加密井地层压力影响因素分析 3.1 裂缝影响根据前面的分析可知王窑区地层的天然裂缝中显裂缝并不多,多数属于隐裂缝,基本处于闭合状态,作为流体运移的通道作用相对较小。虽然试验区以隐性裂缝为主,但是在外应力的诱导下(如钻井、压裂、注水等),部分天然缝破裂成张性缝,增加了储层的渗透率,甚至能起到运移通道作用。根据对试验区王20-0324、王25-053、王25-071的地面微地震报告的分析表明,该区压裂裂缝的趋势主要为北东46.4°~75.1°,裂缝长度160~170 m。
(1) 裂缝长度的影响
分析裂缝半长对地层压力的影响规律,主要研究方式保持其他参数不变,通过改变裂缝半长观察地层压力的变化规律。
从图 3可以看出,在其他裂缝参数保持不变的情况下,加密井最近主裂缝半长与加密井地层压力的变化成正相关,但裂缝半长增至某一值时,地层压力对裂缝半长的敏感度有所减弱。
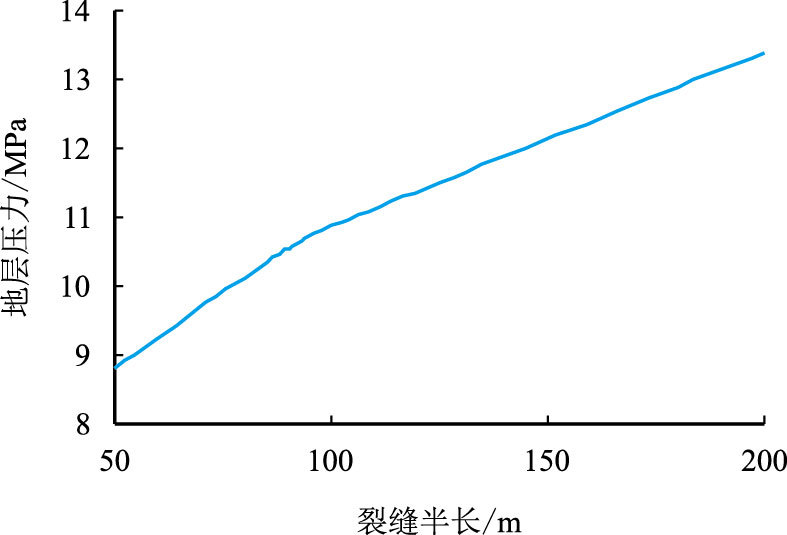 |
| 图3 裂缝半长对加密井王20-042的影响 Fig. 3 The influence to Well Wang 20-042 of infilling in fracture half length |
(2) 裂缝叉分比对地层压力的影响
针对地层裂缝发育程度的研究通常会引用裂缝叉分比,用以衡量地层中裂缝的发育程度,次级微小裂缝的数量受其直接控制。由于无法准确地知道地层所有裂缝的分布情况,特别是微细裂缝的分布,一般情况下,只能知道一些主要裂缝,所以,对裂缝进行研究时,可以利用给出的主裂缝以及裂缝叉分比来模拟裂缝地层中裂缝的分布情况,再通过裂缝的分布规律分析储层流体流动特征及地层压力场特征。
由图 4可见,裂缝叉分比与加密井王20-042的地层压力成正相关,但裂缝叉分比增大到一定程度后,裂缝叉分比对地层压力的影响有所降低。
 |
| 图4 加密井王20-042受裂缝叉分比的影响 Fig. 4 The influence to Well Wang 20-042 of infilling in crack fork points |
选取注水井王20-04和生产井王20-03作为研究对象,分析注水量和产量的改变对王20-042地层压力的影响。模拟不同注水量条件下注水井王20-04对加密井王20-042的地层压力的影响,如图 5所示。
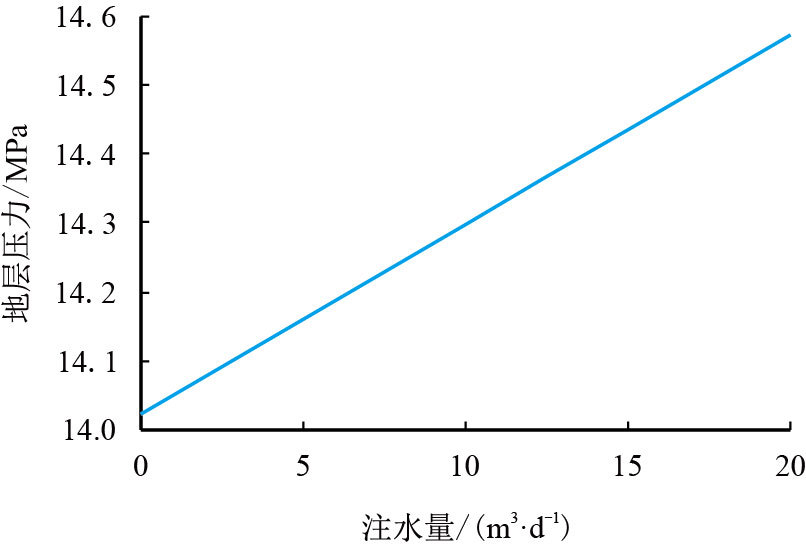 |
| 图5 注水井对加密井地层压力的影响 Fig. 5 The influence of injection wells on infilling well formation pressure |
从图 5可以看出,随着注水井王20-04注水量的增加,加密井王20-042的地层压力几乎成线性增加。如果要使王20-042的地层压力系数控制在1.10左右,则需要将注水井王20-04关井停注。模拟不同产量条件下生产井王20-03对加密井王20-042地层压力的影响,结果如图 6所示。
从图 6可以看出,随着生产井王20-03井采出量的增加,加密井王20-042的地层压力逐渐降低。
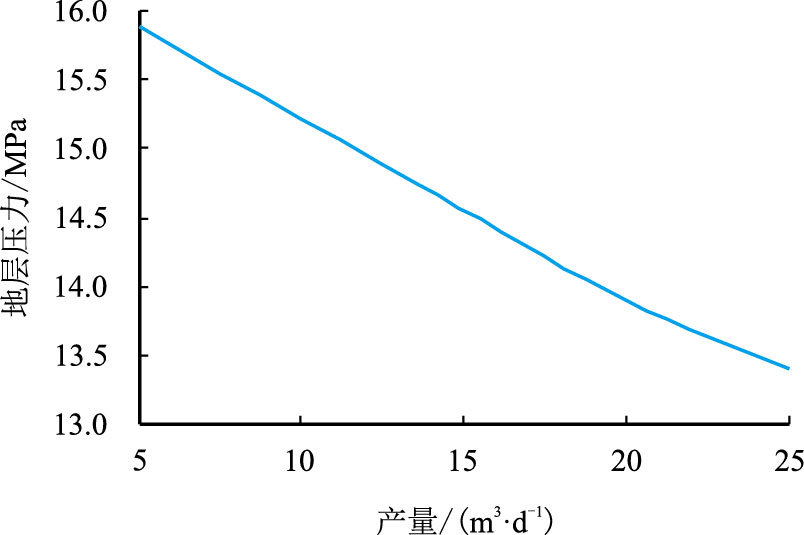 |
| 图6 生产井对加密井地层压力的影响 Fig. 6 Production wells for the Influence of Infill well formation pressure |
(1) 受注水井、生产井的影响,地下流体是时刻流动着的,因此,加密井所在位置的地层压力是动态变化着的;尤其是邻近注采井工作制度发生改变后,加密井地层压力的动态变化规律会变得更加复杂。本项目从压力波在地层中的传播特征出发,描述了加密井地层压力的这一动态变化规律,并建立了相应的定量计算方法。
(2) 引起加密井地层压力异常的原因既有地层自身方面的,也有人为因素造成区域性注采不平衡引起的。加密井地层压力大小受到邻井距离及其工作制度、地层渗流特征以及地层中裂缝分布规律及其发育程度的直接影响,同时与区域注采比有直接关系。
(3) 通过利用复杂地层压力预测软件模拟加密井周围邻井生产制度的改变对目标加密井地层压力的影响规律,可以对油田实际加密井钻井之前应该采取的措施进行指导,以实现对异常地层压力进行快速有效地控制。
| [1] |
黎洪, 彭苏萍, 张德志. 裂缝性油藏主渗透率及主裂缝方向识别方法[J].
石油大学学报(自然科学版), 2002, 26 (2) : 44 –46.
LI Hong, PENG Suping, ZHANG Dezhi. Identificating method for the principal permeability and the direction of fracture in the fractured reservoirs[J]. Journal of the University of Petroleum,China(Edition of Natural Science), 2002, 26 (2) : 44 –46. |
| [2] |
聂立新. 各向异性天然裂缝油藏裂缝方位的确定[J].
石油大学学报(自然科学版), 1997, 21 (6) : 39 –41.
NIE Lixin. Determination of orientation of the fractures in an anisotropic naturally fractured reservoir[J]. Journal of the University of Petroleum, China(Edition of Natural Science), 1997, 21 (6) : 39 –41. |
| [3] |
肖国益, 王秀东, 李连坤, 等. 调整井复杂地层压力预测的新方法[J].
石油钻探技术, 2002, 30 (2) : 7 –9.
XIAO Guoyi, WANG Xiudong, LI Liankun, et al. A new method of predicting formation pressure in adjustment wells[J]. Petroleum Drilling Techniques, 2002, 30 (2) : 7 –9. |
| [4] |
楼一珊, 张学亮, 王语英, 等. 地层坍塌压力预测技术在钟市地区的应用[J].
石油钻探技术, 1999, 27 (3) : 12 –13.
LOU Yishan, ZHANG Xueliang, WANG Yuying, et al. Application of formation caving pressure prediction technology[J]. Petroleum Drilling Techniques, 1999, 27 (3) : 12 –13. |
| [5] |
程远方, 徐同台. 安全泥浆密度窗口的确立及应用[J].
石油钻探技术, 1999, 27 (3) : 16 –18.
CHENG Yuanfang, XU Tongtai. Determination and application of the safe mud density window[J]. Petroleum Drilling Techniques, 1999, 27 (3) : 16 –18. |
| [6] |
程远方, 黄荣樽. 钻井工程中的泥页岩井壁稳定的力学分析[J].
石油大学学报(自然科学版), 1993, 17 (4) : 35 –39.
CHENG Yuanfang, HUANG Rongzun. Shale drilling engineering mechanical wellbore stability analysis[J]. Journal of the University of Petroleum,China(Edition of Natural Science), 1993, 17 (4) : 35 –39. |
| [7] |
张兰江, 夏竹君, 李志勇, 等. 复杂压力系统地层压力预测方法在文东油田的应用[J].
石油钻探技术, 2002, 30 (2) : 16 –18.
ZHANG Lanjiang, XIA Zhujun, LI Zhiyong, et al. Applications of complex formation pressure prediction in Wendong Oilfield[J]. Petroleum Drilling Techniques, 2002, 30 (2) : 16 –18. |
| [8] |
栗广科, 贾振尧. 中原油田深探井钻井技术[J].
断块油气田, 1995, 2 (5) : 40 –44.
LI Guangke, JIA Zhenyao. Drilling teehnology for deep exploration well in Zhongyuan Oilfield[J]. Fault-Block Oil & Gas Field, 1995, 2 (5) : 40 –44. |
| [9] |
栗广科, 赵芳豹. 复杂区块调整井优质快速钻井技术[J].
石油钻探技术, 2003, 31 (1) : 16 –18.
LI Guangke, ZHAO Fangbao. Optimum and fast drilling technique in adjustment wells in complicated block[J]. Petroleum Drilling Techniques, 2003, 31 (1) : 16 –18. |
| [10] |
张兆盈, 张建设, 田绍臣, 等. TP130TT高抗挤套管研究与应用[J].
石油钻探技术, 2002, 30 (2) : 36 –37.
ZHANG Zhaoying, ZHANG Jianshe, TIAN Shaochen, et al. Study and application of TP130TT collapsing casing[J]. Petroleum Drilling Techniques, 2002, 30 (2) : 36 –37. |
| [11] |
刘绍轩, 罗新华, 徐松辽. 储层孔隙压力计算方法研究与应用[J].
大庆石油地质与开发, 2003, 22 (3) : 47 –49.
LIU Shaoxuan, LUO Xinhua, XU Songliao. Applied study on calculating formation pressure[J]. Petroleum Geology & Oilfield Development in Daqing, 2003, 22 (3) : 47 –49. |
| [12] |
梁何生, 闻国峰, 王桂华. 开发井油层孔隙压力动态预测新方法[J].
钻井液与完井液, 2003, 20 (5) : 18 –19.
LIANG Hesheng, WEN Guofeng, WANG Guihua. New method for predieating pore pressure indevelopment wells[J]. Drilling Fluid & Completion Fluid, 2003, 20 (5) : 18 –19. |
| [13] |
郭大立, 赵金洲, 纪禄军. 生产过程中裂缝内压力分布的模拟研究[J].
石油钻采工艺, 2001, 23 (5) : 54 –57.
GUO Dali, ZHAO Jinzhou, JI Lujun. Study on pressure distribution in fracture during producing process[J]. Oil Drilling & Production Technology, 2001, 23 (5) : 54 –57. |
| [14] |
张东海. 调整井地层压力预测方法[J].
石油钻采工艺, 1993 (5) : 13 –15.
ZHANG Donghai. Method of predicting formation pressure in adjustment wells[J]. Oil Drilling & Production Technology, 1993 (5) : 13 –15. |
| [15] |
周东华, 李翠楠, 张庆辉, 等. 裂缝地层调整井压力影响因素研究[J].
钻采工艺, 2011, 34 (1) : 39 –41.
ZHOU Donghua, LI Cuinan, ZHANG Qinghui. Research on prssure influential factors of adjustment well in creviced formation[J]. Drilling & Production Technology, 2011, 34 (1) : 39 –41. |
 2016, Vol. 38
2016, Vol. 38


