2. 中海石油(中国)有限公司湛江分公司, 广东 湛江 524000;
3. 中国石化股份胜利油田分公司, 山东 东营 257015
2. Zhanjiang Branch Co Ltd, CNOOC, Zhanjiang, Guangdong 524000, China;
3. Shengli Oilfield Company, SINOPEC, Dongying, Shandong 257015, China
根据国内外裂缝性碳酸盐岩油藏储层地质特征的调研可知,裂缝性碳酸盐岩油藏所具有的共同特点是储层非均质性极强,储集空间与渗流通道主要以裂缝为主。与常规砂岩油藏相比,裂缝性碳酸盐岩油藏储集空间类型和储层结构更为复杂,因此水驱油过程渗流特征和驱替机理与砂岩油藏相比有很大的差别,开发过程中的生产特征有着自己的特殊性[1-2]。生产过程可能会出现高产能和低产能,甚至无产能的井共存、注水井邻井不见效以及油井生产能力快速下降等现象。
对现有裂缝性碳酸盐岩大尺寸裂缝型渗流物理模型研制成果的文献调研显示[3-7],在实验室进行大尺寸裂缝性碳酸盐岩油藏水驱油渗流特征实验测试研究时,还不能完全模拟真实储层的裂缝发育特征,对裂缝系统中两相流动规律的研究大多采用简化的物理模型来实现,国外很多学者在这方面也做了大量的研究[8-11],但是他们的裂缝系统模型多采用透明的有机合成材料,并且裂缝网络结构简单,与储层真实情况差异较大。
以富台油田储层裂缝发育特征为基础,采用与储层岩石性质相近的天然碳酸盐岩和人造大理石等材料,设计并制作了多组不同裂缝网络系统的大尺寸渗流物理模型;参照非稳定两相流体相对渗透率测试方法行业标准,设计了裂缝系统水驱油实验流程,采用非稳态法对裂缝系统进行油水两相渗流特征和相对渗透率曲线测试研究,并根据实验结果研究了不同裂缝网络结构条件下裂缝宽度与缝网密度对油水相对渗透率的影响。
1 裂缝网络物理模型的提取本次实验物理模型以富台潜山油田车古201区裂缝发育特征为样本,通过对目标区储层地质特征的分析和对地面露头及储层岩芯的观察,获得与富台潜山油田车古201区储层裂缝网络系统相似的裂缝性网络模式。结合富台地区裂缝发育特征,可将裂缝系统按缝宽w划分为4类:w>5.0 mm为大缝;1.0 mm < $w \leqslant$ 5.0 mm为中缝;0.1 mm < $w \leqslant$1.0 mm为细缝;缝宽w ≤ 0.1 mm为微缝。
根据地面露头的观察(图 1),目标区储层裂缝发育具有以下特点:(1) 规则裂缝占主导地位;(2) 裂缝以高角度缝为主。对储层岩芯进行了直接观察、CT扫描以及铸体薄片分析,通过对各个层位的岩芯进行分析,发现车古201区中缝以上级别的裂缝往往被充填,有效缝以细缝、微缝为主,裂缝密度、条数统计结果见表 1,岩芯分析图见图 2。
 |
| 图1 地面露头裂缝走向 Fig. 1 Fracture orientation of the outcrop |
 |
| 图2 目标区域储层岩芯分析 Fig. 2 Core analysis of the target area |
| 表1 目标区域岩芯裂缝参数统计表 Table 1 The fracture parameter of the target area |
目标区储集层的基质的渗透能力极低,裂缝是主要的储集空间和导流空间,为了使物理模型能更好地表征裂缝网络系统对裂缝系统渗流特征的影响,实验物理模型的设计主要参照以下几个准则:(1) 不考虑基质渗透性的影响;(2) 规则裂缝占主导地位;(3) 裂缝以高角度缝为主;(4) 裂缝的宽度以0.1 mm < $w \leqslant$1.0 mm为主。
按照物理模型的尺寸,采用与储层岩石物性相近的碳酸盐岩制作了多个不同裂缝网络结构的模型,其效果见图 3,从裂缝结构上可以分为平行裂缝系统、简单裂缝系统和复杂裂缝系统,模型整体长60.0 cm,宽40.0 cm,厚度1.5 cm,内部裂缝以规则的高角度裂缝为主,并且宽度在0.1~ 1.0 mm(表 2),与矿场实际有一定的相似性。
 |
| 图3 裂缝系统物理模型 Fig. 3 Physical model of fracture system |
| 表2 物理模型分类 Table 2 Physical model classification |
本次研究采用非稳态法进行两相渗流特征和油水相对渗透率实验测试。驱替系统采用升降式水塔提供恒定水压;在模型的上部架设一台摄像机对裂缝网络系统中水驱油的状态以及驱替前缘的推进动态进行实时录像观察;出口端用滴定管精确计量各个时间采出的油、液量。实验装置见图 4。
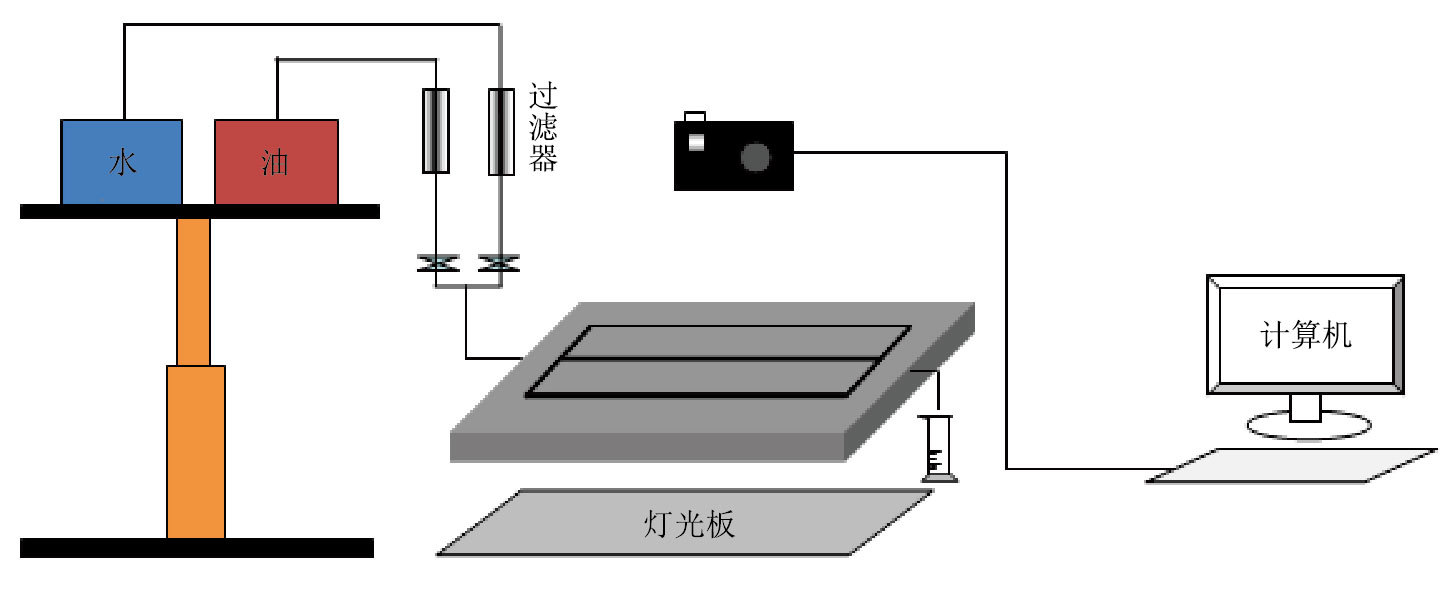 |
| 图4 实验装置和流程示意图 Fig. 4 Schematic diagram of experimental apparatus |
实验过程采用的流体是蒸馏水和模拟油。模拟油的黏度参照目标油田地层油的黏度设计。实验中用到的模拟油为硅油,黏度为4.00 mPa·s,水的黏度为1.08 mPa·s。为了在实验中更好地区分油和水的流动,用苏丹红把油染成红色,水不染色。
3.3 实验步骤实验过程的具体操作步骤如下。
(1) 按图 4连接实验装置,校准仪器。
(2) 对裂缝模型进行抽真空,将模型饱和实验用水,准确记录量筒中水的减少量,计算裂缝系统模型的孔隙体积。
(3) 用实验模拟油驱替模型中的水,准确记录出口端累计采水量,待出口端完全不出水后,认为此时裂缝系统内剩余的水量即为束缚水,然后测量束缚水条件下油相的渗透率,停止油驱水。
(4) 进行水驱油实验,准确记录见水时间、见水时的累积产油量、累积产液量、驱替速度。
(5) 实验过程采用恒压驱替,见水初期,加密记录数据点,随出油量的不断下降,逐渐加长记录的时间间隔。出口含水率大于99%后水驱油过程结束,关闭并清洗实验设备。
4 实验数据处理水驱油实验结束后,根据水驱油过程所测定的注采动态数据计算油水相对渗透率,计算方法采用JBN法[12-14] 和曲线拟合法[15]两种方法进行计算,JBN方法计算步骤请参见两相相渗测试标准。曲线拟合法计算步骤如下。
(1) 作$\Delta p$,$V_{\rm o}$,$V_{\rm w}$ 与t 的关系曲线,把实验数据做一次光滑处理。
(2) 计算$\Psi_{\rm e}$,$\Theta$,$S_{\rm w}$
| $\left\{ \begin{array}{l} \Theta = \dfrac{{\Delta p}}{Q} \times \dfrac{A}{{{\mu _{\rm{o}}}L}}\\ {\Psi _{\rm e}} = 1/{{\overline V }}\\ {S_{\rm w}} = \overline {{V_{\rm{o}}}} + {S_{{\rm{wc}}}} \end{array} \right.$ | (1) |
(3) 用公式逼近$\Theta$—$\Psi_{\rm e}$,$S_{\rm w}$—$\Psi_{\rm e}$
| $\Theta {\rm{ = }}{a_1} + {a_2} \cdot {\Psi _{\rm e}} + {a_3} \cdot \Psi _{\rm e}^2 + {a_4} \cdot \Psi _{\rm e}^3$ | (2) |
| ${S_{\rm{w}}} = {b_1} + {b_2} \cdot {\Psi _3} + {b_3} \cdot \Psi _{\rm e}^2 + {b_4} \cdot \Psi _{\rm e}^3$ | (3) |
| $\alpha {\rm{ = }}{a_1} + 2{a_2} \cdot {\Psi _{\rm e}} + 3{a_3} \cdot \Psi _{\rm e}^2 + 4{a_4} \cdot \Psi _{\rm e}^3$ | (4) |
| $f{\rm{ = 1}} + {b_2} \cdot \Psi _{\rm e}^2 + 2{b_3} \cdot \Psi _{\rm e}^3 + 3{b_4} \cdot \Psi _{\rm e}^4$ | (5) |
| ${S_{\rm e}}{\rm{ = }}{b_1} + 2{b_2} \cdot {\Psi _{\rm e}} + 3{b_3} \cdot \Psi _{\rm e}^2 + 4{b_4} \cdot \Psi _{\rm e}^3$ | (6) |
(4) 求解$K_{\rm ro}$,$K_{\rm rw}$
| ${K_{{\rm{ro}}}} = \dfrac{{1 - f}}{a}$ | (7) |
| ${K_{{\rm{rw}}}} = \dfrac{f}{a} \cdot \dfrac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{o}}}}}$ | (8) |
根据裂缝系统油水相对渗透率计算结果绘制相应的油水相对渗透率曲线,并把相渗曲线按照裂缝网络结构进行分类,分析裂缝系统中不同裂缝宽度与不同缝网密度对油水相对渗透率的影响。
5.1 不同裂缝宽度的影响为了研究裂缝系统中裂缝宽度对相渗曲线的影响,实验中测量了裂缝结构简单与复杂两种情况下,不同裂缝宽度对应的裂缝系统的油水相对渗透率,各裂缝系统的相对渗透率曲线如图 5、图 6所示,图中数据点为JBN方法计算结果,实线为曲线拟合法计算结果。
图 5为3种裂缝组合方式的平行裂缝系统相渗曲线。随着裂缝宽度的增大,油相相渗曲线下凹程度逐渐减小,水相相渗曲线的上凸程度减小,等渗点逐渐向右移动,曲线特征逐渐向斜交直线型过渡。除此之外,两相共渗区的范围受裂缝宽度极差的影响,缝宽极差较大时,宽缝会对窄缝内的水驱油过程形成一定的“屏蔽”作用,缝宽极差越大,屏蔽作用越明显,窄缝内剩余油饱和度越大。
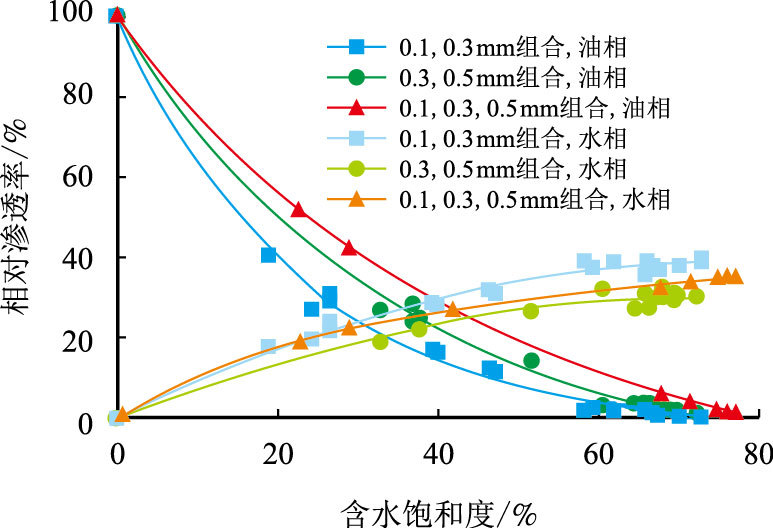 |
| 图5 简单平行裂缝系统相渗曲线 Fig. 5 Relative permeability curves of parallel fracture system |
图 6为两组复杂缝网系统的相渗曲线。可以看出,随着裂缝宽度增大,复杂缝网系统相渗曲线下凹程度减小,两相共渗区范围也逐渐增大。
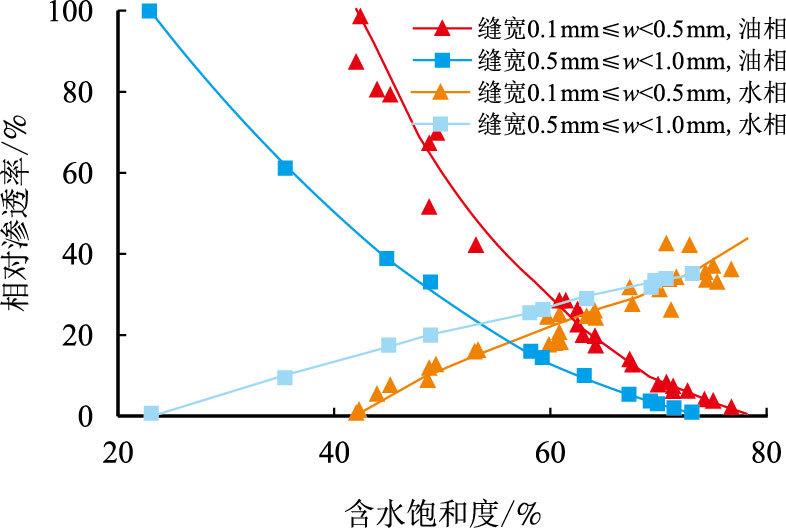 |
| 图6 复杂缝网系统相渗曲线 Fig. 6 Relative permeability curves of complex fracture system |
实验结果表明,平均裂缝宽度较小时,裂缝系统内的水驱前缘稳定性较差,水相沿高渗带突进现象严重,裂缝系统含水采油阶段所占比重较大,相渗曲线表现出下凹程度较大的趋势;平均裂缝宽度较大时,裂缝系统内水驱前缘突进平稳,无水采油阶段比重较大,相渗曲线表现出由凹型向斜交直线型相渗曲线形态接近的趋势。
根据裂缝宽度与渗流阻力的关系,平均裂缝宽度较小时,驱替前缘进入裂缝空间的阻力较大,使得窄缝系统容易保存裂缝内的流体,一方面导致了束缚水饱和度的增大,另一方面容易降低裂缝系统的驱油效率;而对于宽度较大且连通较好的裂缝系统,水驱油程度较高,剩余油含量较少,从而使得两相共渗区范围扩大。
5.2 不同裂缝密度的影响为了研究裂缝系统中裂缝密度(模型单位面积上的裂缝条数和裂缝相交节点数)对相渗曲线的影响,实验中测量了平均裂缝宽度相近的情况下,裂缝系统逐渐由简单平行缝系统模型到两种复杂程度不同的裂缝网络系统模型时的油水相对渗透率,对应的相对渗透率曲线如图 7所示(3组模型裂缝宽度均以0.1~0.5 mm为主)。
从图 7可以看,随着裂缝密度的逐渐增大,相渗曲线出现等渗点右移、两相共渗区变窄的趋势;当裂缝密度增大时,相渗曲线特征会趋向于砂岩相渗曲线的特征(如图中复杂裂缝网络相渗曲线),水相相渗曲线也由凸型逐渐向凹型过渡。
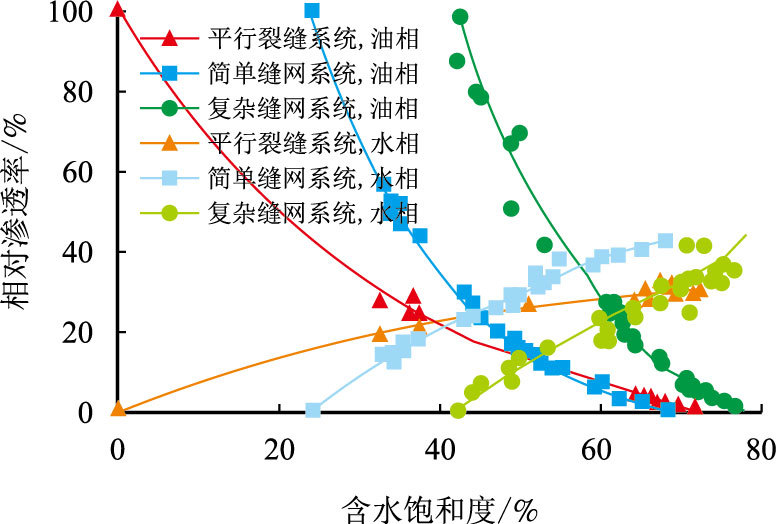 |
| 图7 不同裂缝系统的油水相渗曲线 Fig. 7 Relative permeability curves of different fracture systems |
在复杂裂缝网络系统中,水驱前缘经过每一个裂缝交汇处都相当于经过一组多向度交叉裂缝流动,也就导致了在裂缝宽度极差相近的情况下,裂缝密度越大,束缚水饱和度和残余油饱和度越大,两相共渗区范围越窄;而且从相似的角度来讲,较复杂的裂缝网络系统可以等效为砂岩的多孔介质系统的渗流状态,所以复杂裂缝网络系统相渗曲线会呈现出多孔介质系统相渗曲线的特征。
5.3 实验结果与国外研究成果的对比根据国外学者的研究结论,如图 8中 Romm曲线与裂缝系统曲线,图中Romm曲线是简单平行缝系统理想情况下,宽度较大且驱替方向与裂缝走向平行的相渗曲线;裂缝系统曲线为裂缝较窄且裂缝走向随机时的相渗曲线形态[15]。可以看出,裂缝系统由简单到复杂,并且裂缝宽度变窄时,裂缝系统的相渗曲线两相共渗区变窄,曲线形态由直线型向凹型过渡。
根据本次实验结果的相渗曲线规律(图 8中窄缝网络与宽缝网络曲线),复杂裂缝网络系统中,平均裂缝宽度越大,相渗曲线越向Romm曲线靠近;平均裂缝宽度越窄,相渗曲线也出现下弯的趋势,同时两相共渗区范围越小,结合不同裂缝密度的相渗曲线规律可以发现,研究结果与国外学者所得认识一致。
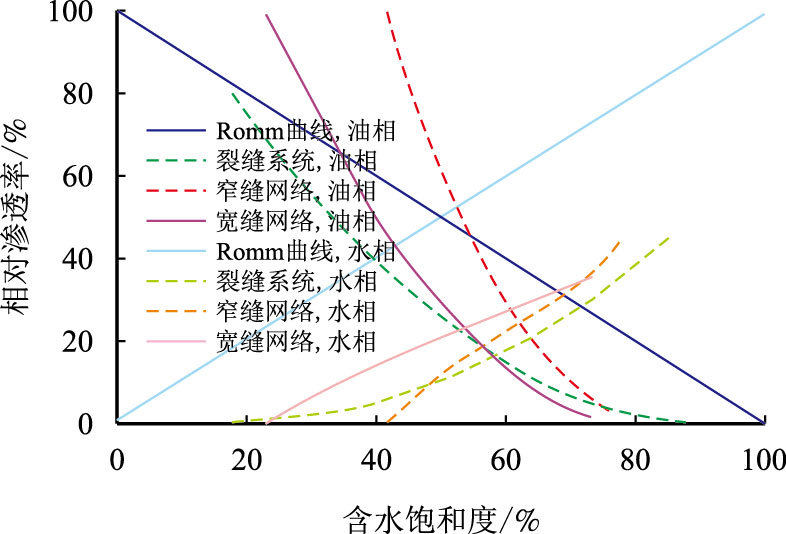 |
| 图8 相渗曲线对比 Fig. 8 The difference of relative permeability curves |
(1) 同一裂缝系统,裂缝平均宽度越大,裂缝越均匀,水驱前缘稳定性越大,油相相对渗透率曲线由下弯型向直线型靠近,水相相对渗透率曲线也逐渐向直线型过渡。
(2) 同一裂缝系统,裂缝平均宽度越窄,驱替前缘进入裂缝空间阻力越大,束缚水饱和度与残余油饱和度也就越大,两相共渗区范围越窄。
(3) 平行裂缝系统中,由于裂缝宽度极差的影响,宽缝会对窄缝内的流动起到“屏蔽”作用,裂缝宽度极差越大,屏蔽作用越明显。
(4) 裂缝网络系统中,水驱前缘经过每一个裂缝交汇处都相当于一组多向度交叉裂缝流动;裂缝密度越大,束缚水饱和度和残余油饱和度越大,等渗点位置越向右移动,两相共渗区范围越窄。
(5) 裂缝网络系统越复杂,渗流就越趋向于砂岩多孔介质系统的渗流,复杂裂缝网络系统相渗曲线趋向于多孔介质系统相渗曲线。
符号说明
$\Delta p$—压差,MPa;
$V_{\rm{o}}$—累计采油量,mL;
$V_{\rm{w}}$—累计产水量,mL;
t—时间,s;
$\Psi_{\rm e}$—含水率导数,无因次;
$\Theta$—两相总阻力与单相阻力的比值,无因次;
$S_{\rm w}$—含水饱和度,%;
Q—流量,cm3/s;
A—岩芯横截面积,cm2;
$\mu_{\rm o}$—油相黏度,mPa·s;
L—长度,m;
${\overline V }$—无因次累积采液量;
${\overline V_{\rm o} }$—无因次累积采油量;
$S_{\rm wc}$—束缚水饱和度,%;
a1,a2,a3,a4,b1,b2,b3,b4—多项式拟合系数,无因次;
f—含水率,%;
$S_{\rm e}$—岩芯出口端面含水饱和度,%;
${K_{{\rm{ro}}}}$—油相相对渗透率,%;
${K_{{\rm{rw}}}}$—水相相对渗透率,%;
$\alpha$—两相阻力系数,无因次;
$\mu_{\rm w}$—水相黏度,mPa·s。
| [1] |
廉培庆, 程林松, 刘丽芳. 裂缝性碳酸盐岩油藏相对渗透率曲线[J].
石油学报, 2011, 32 (6) : 1026 –1030.
LIAN Peiqing, CHENG Linsong, LIU Lifang. The relative permeability curve of fractured carbonate reservoirs[J]. Acta Petrolei Sinica, 2011, 32 (6) : 1026 –1030. |
| [2] |
谢俊, 张金亮.
剩余油描述与预测[M]. 北京: 石油工业出版社, 2003 : 16 -22.
XIE Jun, ZHANG Jinliang. Description and prediction of remaining oil[M]. Beijing: Petroleum Industry Press, 2003 : 16 -22. |
| [3] |
郑小敏, 孙雷, 王雷, 等. 缝洞型碳酸盐岩油藏水驱油机理物理模拟研究[J].
西南石油大学学报(自然科学版), 2010, 32 (2) : 89 –92.
ZHENG Xiaomin, SUN Lei, WANG Lei, et al. Physical simulation of water displacing oil mechanism for vuggy fractured carbonate rock reservoir[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2010, 32 (2) : 89 –92. |
| [4] |
李爱芬, 孙强, 张东, 等. 单一缝洞内油水相对渗透率及其影响因素[J].
中国石油大学学报(自然科学版), 2013, 37 (3) : 98 –102.
LI Aifen, SUN Qiang, ZHANG Dong, et al. Oilwater relative permeability and its influencing factors in single fracture-vuggy[J]. Journal of China University of Petroleum, 2013, 37 (3) : 98 –102. |
| [5] |
王世洁. 基于真实岩芯刻蚀模型的缝洞油藏水驱油机理[J].
西南石油大学学报(自然科学版), 2011, 33 (6) : 75 –79.
WANG Shijie. Study on the water flooding mechanism of carbonate fracture-cavity reservoir based on real core etching model[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2011, 33 (6) : 75 –79. |
| [6] |
李鹴, 李允. 缝洞型碳酸盐岩孤立溶洞注水替油实验研究[J].
西南石油大学学报(自然科学版), 2010, 32 (1) : 117 –120.
LI Shuang, LI Yun. An experimental research on water injection to replace the oil in isolatedcaves in fracturecavity carbonate rock oil field[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32 (1) : 117 –120. |
| [7] |
王雷, 窦之林, 林涛, 等. 缝洞型油藏注水驱油可视化物理模拟研究[J].
西南石油大学学报(自然科学版), 2011, 33 (2) : 121 –124.
WANG Lei, DOU Zhilin, LIN Tao, et al. Study on the visual modeling of water flooding in carbonate fracturedcavity reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33 (2) : 121 –124. |
| [8] | CHEN C, HORNE R N, FOURAR M. Experimental study of two-phase flow structure effects on relative permeabilities in a fracture[C]//Twenty-ninth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, California, 2004. |
| [9] | SHAD S,MAINI B B,GATES I D. Effect of fracture and flow orientation on two-phase flow in an oil-wet fracture:Relative permeability curves and flow structures[C]. SPE 132229, 2010. |
| [10] | ALTURKI A A, MAINI B B, GATES I D. The effect of fracture aperture and flow rate ratios on two-phase flow in smooth-walled single fracture[J]. Journal of Petroleum Exploration and Production Technology, 2013, 3 (2) : 119 –132. DOI:10.1007/s13202-012-0047-5 |
| [11] | PERSOFF P, PRUESS K. Two-phase flow visualization and relative permeability measurement in natural roughwalled rock fractures[J]. Water Resources Research, 1995, 31 (5) : 1175 –1186. DOI:10.1029/95WR00171 |
| [12] |
易敏, 郭平, 孙良田. 非稳态法水驱气相对渗透率曲线实验[J].
天然气工业, 2007, 27 (10) : 92 –94.
YI Min, GUO Ping, SUN Liangtian. An experimental study on relative permeability curve for unsteady-state gas displacement by water[J]. Natural Gas Industry, 2007, 27 (10) : 92 –94. |
| [13] |
沈平平. 驱替实验计算相对渗透率方法综述[J].
石油勘探与开发, 1982, 6 (3) : 73 –80.
SHEN Pingping. A review of the dynamic methods to determine relative permeability of reservoir rocks[J]. Petroleum Exploration and Development, 1982, 6 (3) : 73 –80. |
| [14] |
PANG Qiqiang. The research for relative permeability calculation method[D]. Chengdu:Southwest Petroleum University, 2011.
庞启强. 相对渗透率计算方法研究[D]. 成都:西南石油大学, 2011. |
| [15] |
T D Van Golf-racht. Fracture reservoir engineering foundation[M]. CHENG Zhongxiang,Translate. Beijing:Petroleum Industry Press, 1989.
T D范高尔夫-拉特. 裂缝油藏工程基础[M]. 陈钟祥, 译. 北京:石油工业出版社, 1989. |
 2016, Vol. 38
2016, Vol. 38


