2. 中国石油西南油气田分公司勘探开发研究院, 四川 成都 610041
2. Research Institute of Petroleum Exploration & Development, Southwest Oil and Gas Field Company, PetroChina, Chengdu, Sichuan 610041, China
低渗透油藏孔喉结构复杂,具有强烈的非均质特性。在井周围往往存在岩石和流体物性不同的两个或两个以上的复合油藏区域。对于复合油藏的试井分析,国内外学者进行了大量的研究。1989年,Olarewaiu J S和Lee W J分别对定产量和定压生产的双区复合油藏渗流模型,利用Laplace变换进行了求解,并对双区特性差异的典型曲线进行了分析[1];1995年,Kuchuk F J和Habashy T M建立了岩石和流体物性径向变化的复合油藏渗流模型,利用点源函数和镜像反映法求出了模型的解析解[2];2009年,Feng J等基于等值渗流阻力法建立非均质复合天然裂缝性油藏渗流模型,分析了裂缝参数对压力动态的影响[3];中国学者宁正福、刘启国和李汝勇等对复合油气藏的渗流和试井分析进行了相关研究,并取得了一定成果[4-6]。但上述研究均采用线性渗流模型刻画地层渗流,没有考虑到低渗透储层低速非达西渗流特性。针对低渗透储层渗流特性,2010年,Sun Q Y等引入有效半径方法,建立考虑启动压力梯度的非达西流动下的复合储层渗流模型,绘制非达西渗流样板曲线,并对参数敏感性进行了分析[7];2011年,Lu J等指出Laplace变换对非线性渗流方程不适用,通过格林函数和数值逼近求解了低渗透储层非线性渗流模型[8]。 近年来,随着低渗透储层的大量开发投产,中国学者对低速非线性渗流问题进行了大量研究,程时清、王晓冬等引入“动边界”的概念描述低渗透储层的流动扩散问题[9-10];2011年,方甲中等建立了考虑动边界的复合油藏低速非达西渗流模型,并采用数值方法刻画动边界的传播[11]。但文献[12]指出,动边界的存在,将形成压力传播不连续的奇点。
随着油田开发的深入,储层条件和地下流体渗流特征日趋复杂,通过解析方法获得准确结果变得更困难。国内外学者采用数值方法求解复杂渗流问题。Guo J、程林松等分别采用边界元和有限差分法求解复合油藏渗流问题[13-14];同二者相比,有限元方法采用近似函数求解,精度较高,同非结构化网格剖分相结合,可以方便地处理复杂边界条件下的渗流问题[15]。
在前人研究的基础上,基于低渗透油藏低速非线性渗流模型,考虑井筒储集和表皮效应的影响,建立双区复合油藏直井不稳定渗流数学模型,采用有限元方法对其进行求解,获得井底压力随时间的变化规律,绘制无因次压力及压力导数与时间的双对数曲线并进行参数敏感性分析。
1 物理模型和数学模型 1.1 物理模型图 1所示为一上下边界封闭二区复合油藏完全射开直井示意图。基本假设如下:地层中存在两种不同物性参数渗流区,内外区孔隙度分别为$\phi_1$,$\phi_2$,内外区半径为$r_{\rm 1e}$,$r_{\rm 2e}$;储层厚度为h;不考虑流体重力以及温度变化的影响,该油井以恒定产量$q_{\rm o}$(地面产量)从$t=0$时刻开始生产。
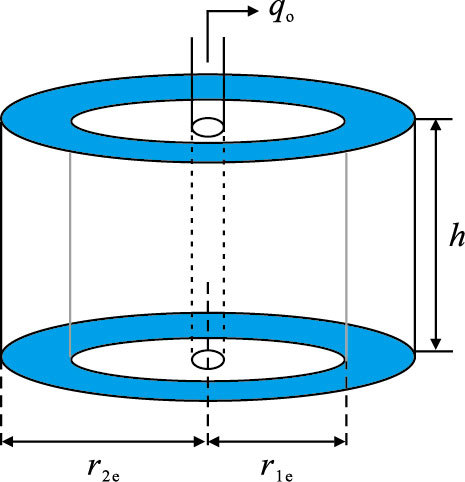 |
| 图1 复合油藏完全射开直井物理模型 Fig. 1 The scheme of vertical well in composite reservoir |
低渗透油藏储层比较致密,渗透性差,井的产能低,渗流特征表现出明显的低速非达西流动现象,既渗流特征曲线并不是过原点的直线,而是按照曲线$AD$变化到直线段,如图 2a所示。
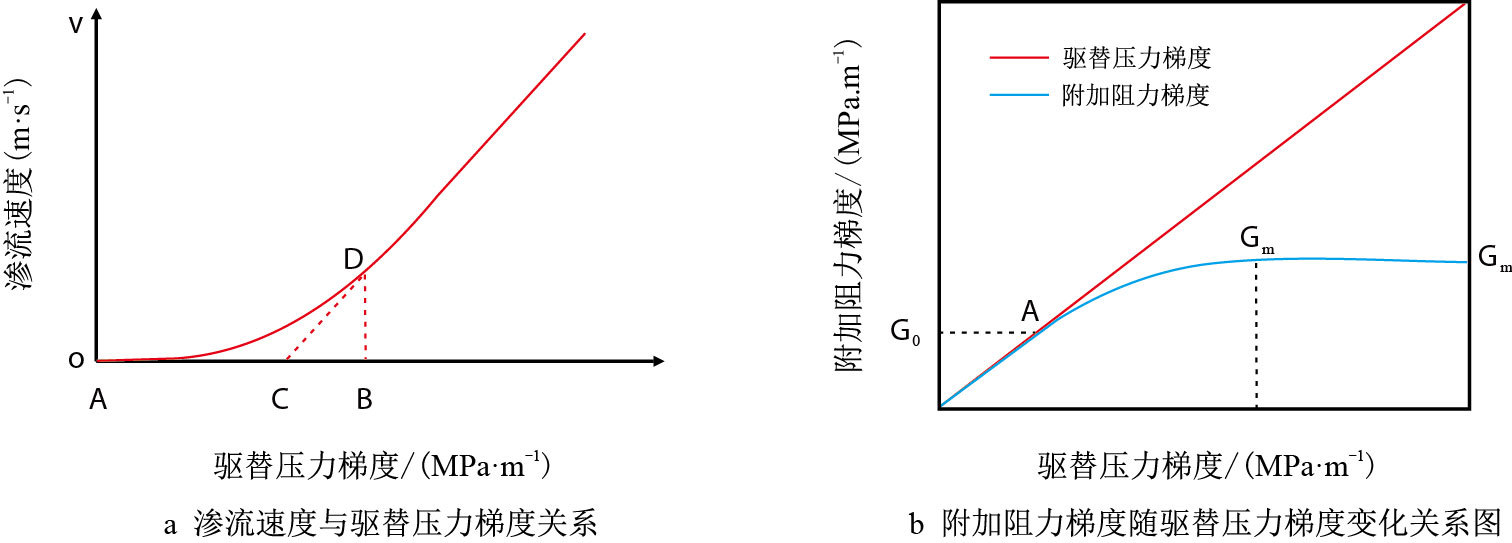 |
| 图2 低渗透油藏渗流特征曲线 Fig. 2 The curves of flow in low permeability reservoir |
驱替压力梯度必须大于A点对应的压力梯度值流体才能开始流动,当驱替压力梯度达到B点对应的压力梯度值时,渗流开始遵循线性渗流。对于考虑启动压力梯度的渗流问题,一些学者认为启动压力梯度为一定值[16],采用流体线性渗流段的反向延长线与压力梯度轴的交点(C点),即拟启动压力梯度值来表示。运动方程可描述为
| $v = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {\beta \lambda \left( {\nabla p - {G_{\rm{m}}}} \right),}&{(\nabla p > {G_{\rm{m}}})} \end{array}}\\ {\begin{array}{*{20}{c}} {0,}&{(\nabla p \le {G_{\rm{m}}})} \end{array}} \end{array}} \right.$ | (1) |
由式(1)可知,存在启动压力梯度的渗流速度与压力梯度的关系仍然是一条直线,只不过直线发生了平移而已。因此,式(1)不能描述图 2a中的曲线段$AD$。本文认为,低速非达西渗流是由于岩石和流体作用引起的额外附加阻力造成的,在渗流过程中,附加阻力梯度不是一个恒定的值,而是随渗流速度和流度的变化而变化[17]。如图 2b所示,附加阻力梯度在整个渗流过程中都是存在的,其数值的大小从0增大到最大附加阻力梯度,压力传播是连续的,避免了奇点的出现。由此得到考虑附加阻力的运动方程为
| $v = \beta \lambda \left( {\nabla p - G} \right)$ | (2) |
在文献[18]的基础上,采用式(3)所示的二次曲线方程描述$AD$段,并由长庆油田低渗透油藏岩芯驱替实验数据,回归出系数a、b和c值。
| $v = a{\left( {\nabla p} \right)^2} + b\nabla p + c$ | (3) |
其中: $a = 0.1223{\lambda ^2} + 2.607 \times {10^{ - 2}}\lambda + 6.659 \times {10^{ - 4}}$,${R^2} = 0.9906$;
$b = 0.0082\lambda - 2.103 \times {10^{ - 5}}$,${R^2} = 0.9691$;
$c = - {10^{ - 5}}{\lambda ^2} - 2 \times {10^{ - 5}}\lambda - 8 \times {10^{ - 7}}$,${R^2} = 0.9627$。
联合式(2)和式(3),推导附加阻力梯度与驱替压力梯度的关系式为
| $G = - \dfrac{{a{{(\nabla p)}^2} + (b - \beta \lambda )\nabla p + c}}{{\beta \lambda }}$ | (4) |
当式(1)中的速度v取0时,可以推得启动压力梯度值为
| ${G_0} = \dfrac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}$ | (5) |
最大附加阻力梯度(拟启动压力梯度)可由式(3)中的抛物线顶点值表示
| ${G_{\rm{m}}} = \dfrac{{ - 4ac + {{(b - \beta \lambda )}^2}}}{{4\beta a\lambda }}$ | (6) |
对应的驱替压力表示为
| $\nabla {p_{\rm{m}}} = \dfrac{{\beta \lambda - b}}{{2a}}$ | (7) |
通过以上分析,考虑附加阻力梯度影响的特低渗透油藏低速非达西渗流规律(式(2))中附加阻力梯度表示为
| ${\kern 21pt}G = \left\{ \begin{array}{l} \nabla p ,{\kern 140pt}\left({\nabla p \leqslant {G_0}}\right)\\[6pt] - \dfrac{{a{{(\nabla p)}^2} + (b - \beta \lambda )\nabla p + c}}{{\beta \lambda }} ,{\kern 40pt} \left({{G_0} \leqslant \nabla p < \nabla {p_{\rm{m}}}}\right)\\[6pt] \dfrac{{ - 4ac + {{(b - \beta \lambda )}^2}}}{{4\beta a\lambda }} ,{\kern 80 pt} \left(\nabla p \geqslant \nabla {p_{\rm{m}}}\right) \end{array} \right.$ | (8) |
在物理模型基础上,基于物质平衡原理,结合流动方程和连续性方程,推导不稳定渗流数学模型。同时,考虑表皮效应的影响,引入有效井半径$r_{\rm we}=r_{\rm w}^{-s}$,以内区参数为基准定义无因次变量
| $\begin{array}{l} {t_{\rm{D}}} = \frac{{3.6{\lambda _1}t}}{{{c_{\rm{t}}}_1{\phi _1}r_{{\rm{we}}}^2}};\\ {r_{{\rm{1D}}}} = \frac{{{r_{{\rm{1e}}}}}}{{{r_{{\rm{we}}}}}};\\ {r_{{\rm{2D}}}} = \frac{{{r_{{\rm{2e}}}}}}{{{r_{{\rm{we}}}}}};\\ {M_{21}} = \frac{{{\lambda _2}}}{{{\lambda _1}}};\\ {\eta _{{\rm{rD}}}} = \frac{{{c_{{\rm{t}}2}}{\phi _2}}}{{{c_{{\rm{t}}1}}{\phi _1}}};\\ {G_{\rm{D}}} = \frac{{{\lambda _1}{r_{{\rm{we}}}}G}}{{1.842 \times {{10}^{ - 3}}{q_{\rm{o}}}B}};\\ {C_{\rm{D}}} = \frac{C}{{2\pi {\phi _1}{c_{{\rm{t1}}}}hr_{{\rm{we}}}^{\rm{2}}}};\\ {p_{\rm{D}}} = \frac{{{\lambda _{\rm{1}}}h}}{{1.842 \times {{10}^{ - 3}}{q_{\rm{o}}}B}}\left[ {{p_{\rm{i}}} - p\left( {r,t} \right)} \right]. \end{array}$ |
描述复合油藏流动的控制方程为:
内区
| $\dfrac{{{tial ^2}{p_{1{\rm{D}}}}}}{{tial r_{\rm{D}}^2}}\! + \!\dfrac{1}{{{r_{\rm{D}}}}}\dfrac{{tial {p_{1{\rm{D}}}}}}{{tial {r_{\rm{D}}}}} \!-\! \dfrac{{{G_{1{\rm{D}}}}}}{{{r_{\rm{D}}}}} \!=\! \dfrac{{tial {p_{1{\rm{D}}}}}}{{tial {t_{\rm{D}}}}},{\kern 5pt}\left( {1 \!\leqslant\! {r_{\rm{D}}} \!<\! {r_{1{\rm{D}}}}} \right)$ | (9) |
外区
| $\begin{array}{l} \frac{{tia{l^2}{p_{{\rm{2D}}}}}}{{tialr_{\rm{D}}^2}} + \frac{1}{{{r_{\rm{D}}}}}\frac{{tial{p_{{\rm{2D}}}}}}{{tial{r_{\rm{D}}}}} - \frac{{{G_{{\rm{2D}}}}}}{{{r_{\rm{D}}}}} = \frac{{{\eta _{{\rm{rD}}}}}}{{{M_{21}}}}\frac{{tial{p_{2{\rm{D}}}}}}{{tial{t_{\rm{D}}}}},\\ ({r_{{\rm{1D}}}} \le {r_{\rm{D}}} < {r_{{\rm{2D}}}}) \end{array}$ | (10) |
初始条件
| ${p_{\rm{D}}}\left( {{r_{\rm{D}}},0} \right) = 0$ | (11) |
考虑井筒储集效应的内边界条件为
| $\dfrac{{tial {p_{\rm{D}}}}}{{tial {r_{\rm{D}}}}}\left| {_{{r_{\rm{D}}} = 1}} \right. = - 1 + {G_{1{\rm{D}}}}\left| {_{{r_{\rm{D}}} = 1}} \right. + {C_{\rm{D}}}\dfrac{{{\rm d}{p_{{\rm{wD}}}}}}{{{\rm d}{t_{\rm{D}}}}}$ | (12) |
外边界条件
| ${\rm{ }}\left\{ \begin{array}{l} {p_{\rm{D}}}\left| {_{{r_{\rm{D}}} \to \infty }} \right. = 0 ,{\kern 28pt} \left( 无限大地层\right)\\ {\rm{ }}{p_{\rm{D}}}\left| {_{{r_{{\rm{eD}}}}}} \right. = 0 ,{\kern 38pt} \left( 定压边界\right)\\ {\rm{ }}\dfrac{{tial {p_{\rm{D}}}}}{{tial n}}\left| {_{{r_{{\rm{eD}}}}}} \right. = 0 ,{\kern 30pt} \left( 封闭边界\right) \end{array} \right.$ | (13) |
由于低渗透油藏的非达西渗流特征,使得由传统的连续“点源”法通过构造函数来求解低渗透双区复合油藏渗流问题变得十分困难。本文采用有限元方法对上述问题进行数值求解,如图 3所示,采用非结构化网格对双区复合油藏进行网格离散,为了保证计算精度,需要对井周围进行加密处理,得到三角形单元数为:1 822,节点个数为:936。
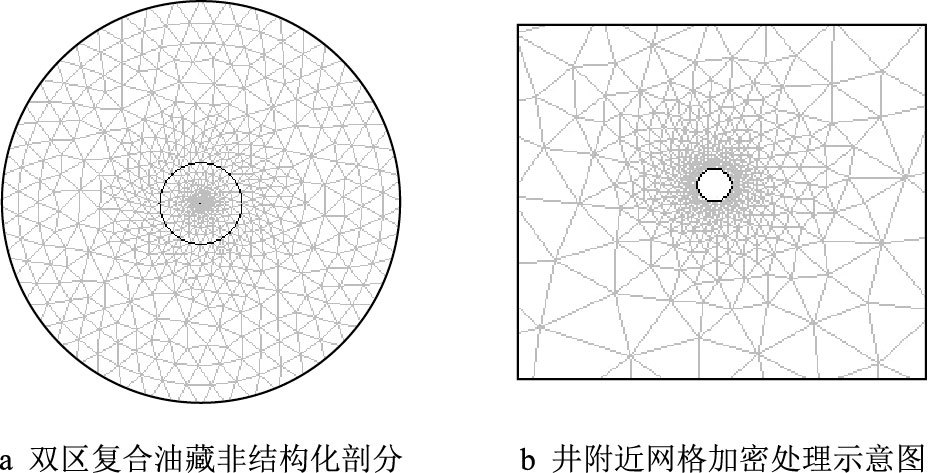 |
| 图3 复合油藏非结构化网格剖分示意图 Fig. 3 The scheme of unstructured mesh of composite reservoir |
应用Galerkin(伽辽金)方法推导有限元积分方程,时间上采用无条件稳定的向后差分方式。为了提高单元插值函数的计算精度,插值多项式应尽量选择完全多项式,但是完整多项式的项数和单元的自由度数有时并不相同,通常采用减少多项式项数的方法,同时保持多项式的对称性。文献[15]指出,采用增加单元节点数的四边形和六面体等高次单元,在网格数目达到一定之后,对解的精度提高作用不大,却大大增加了计算难度。因此,选择二维三角形单元为母单元,3个节点($i,j,k$)权函数取差值函数$N_l=a_l+b_lx+c_ly$($l=i,j,k$),选取任意网格单元进行单元特性分析。
内区
| $\begin{array}{l} {N_l}\left[ {\frac{{tia{l^2}{p_{1{\rm{D}}}}}}{{tialr_{\rm{D}}^2}} + \frac{1}{{{r_{\rm{D}}}}}\left( {\frac{{tial{p_{1{\rm{D}}}}}}{{tial{r_{\rm{D}}}}} - {G_{1{\rm{D}}}}} \right) - \frac{{tial{p_{1{\rm{D}}}}}}{{tial{t_{\rm{D}}}}}} \right]{\rm{d}}\Omega = 0\\ \left( {l = i,j,k} \right) \end{array}$ | (14) |
外区
| $\begin{array}{l} {_\Omega }{N_l}\left[ {\frac{{tia{l^2}{p_{{\rm{2D}}}}}}{{tialr_{\rm{D}}^2}} + \frac{1}{{{r_{\rm{D}}}}}\left( {\frac{{tial{p_{{\rm{2D}}}}}}{{tial{r_{\rm{D}}}}} - {G_{{\rm{2D}}}}} \right) - \frac{{{\eta _{{\rm{rD}}}}}}{{{M_{21}}}}\frac{{tial{p_{2{\rm{D}}}}}}{{tial{t_{\rm{D}}}}}} \right] \cdot \\ \left( {l = i,j,k} \right) \end{array}$ | (15) |
式中:A—三角形网格单元面积
| $%\begin{array}{l} A = \dfrac{1}{2}\left| \begin{array}{l} 1{\kern 8pt}{x_{{i}}}{\kern 8pt}{y_{{i}}}\\ 1{\kern 8pt}{x_{{j}}}{\kern 8pt}{y_{{j}}}\\ 1{\kern 8pt}{x_{{k}}}{\kern 8pt}{y_{{k}}} \end{array} \right|\\[6pt] {\kern 40pt} {\rm{ }} = \dfrac{1}{2}\left( {{x_{{i}}}{y_{{j}}} + {x_{{j}}}{y_{{k}}} + {x_{{k}}}{y_{{i}}} - {x_{{i}}}{y_{{k}}} - {x_{{j}}}{y_{{i}}} - {x_{{k}}}{y_{{i}}}} \right)\\[6pt] {\kern 40pt} {\rm{ }} = \dfrac{1}{2}\left( {{b_{{i}}}{c_{{j}}} - {b_{{j}}}{c_{{i}}}} \right) %\end{array}$ | (16) |
当流体流度一定时,附加阻力梯度随驱替压力梯度的变化而变化,在地层中不同位置处的附加阻力梯度不同,采用解析方法难以求解。而有限元方法可以方便地求解任意网格单元内的压力梯度,结合式(7)求解附加阻力梯度,并带入到下一时步中,求解压力方程。压力梯度的有限元计算格式为
| $\nabla {p_{\rm{D}}} = \nabla N_l \cdot {p_{\rm{D}}}$ | (17) |
考虑边界条件的影响,将边界影响项补充到单元方程组中。若选取的单元为不含边界单元,则单元特征分析后处理为(0,0,0)$^{\rm T}$ 向量;若为第一类边界,则通过置大数法或者置1法强制赋值计算结果;若为第二类边界,则边界影响项化成向量形式为
| ${\smallint _{ij}}{N_l}\frac{{tial{p_{\rm{D}}}}}{{tial{r_{\rm{D}}}}}{\rm{d}}s = \frac{1}{2}{v_{{\rm{tD}}}} \cdot \left( {\begin{array}{*{20}{c}} {{s_{ij}}}\\ {{s_{ij}}}\\ 0 \end{array}} \right)$ |
对于封闭不渗透边界,则边界影响项依旧处理为(0,0,0)$^{\rm T}$向量。同时,采用非结构化网格和有限元方法求解复合油藏问题,不需要给出内外区接触面上的边界条件,便于求解。
通过组装整体矩阵和列阵,建立相应的整体方程组,求解方程组便能得到各个时刻的压力值。同时,考虑到时间步长与渗流阶段和油藏条件相适应,采用自动适应时间步长方法使计算结果更加准确[19]。
2 低渗透复合油藏压力动态分析 2.1 有限元算法正确性验证为了验证本文所采用的有限元算法的正确性,在不考虑附加阻力的情况下,将计算结果与采用连续“点源”法的解析解结果所绘制的无因次压力动态曲线进行了对比验证。如图 4所示,在不考虑附加阻力的情况下,两种方法所得到的双区复合油藏直井井底压力动态曲线吻合较好,表明本文的方法是切实可行的。
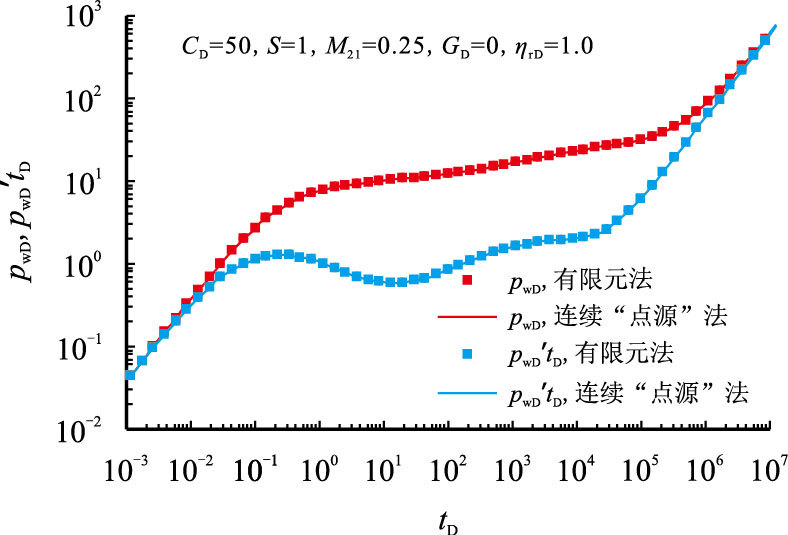 |
| 图4 有限元方法与连续点源法对比验证 Fig. 4 Comparison of type curves between this model and continuous point source method |
针对低渗透油藏渗流特征,分别采用附加阻力法和拟启动压力梯度法处理低渗透油藏低速非线性渗流问题,绘制复合油藏井底压力动态曲线,如图 5所示。
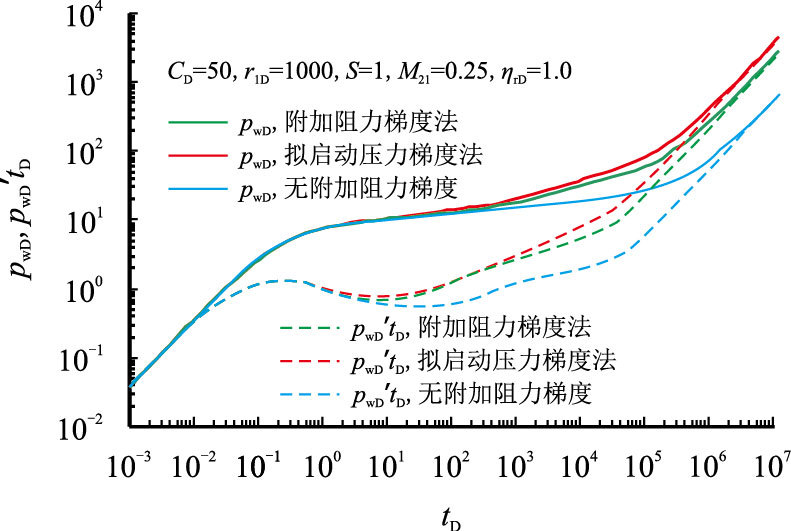 |
| 图5 附加阻力梯度对压力动态的影响 Fig. 5 Type curves of well test affected by AR |
由图 5可知:附加阻力梯度主要影响径向流动阶段,使压力及压力导数曲线上翘;同附加阻力梯度法相比,传统的拟启动压力梯度法忽略了非线性渗流的曲线阶段,始终以最大附加阻力梯度(拟启动压力梯度)代表压力损失,将使得压力及压力导数曲线上翘时间越早,上翘得越厉害。
2.3 内区无因次半径对井底压力动态的影响当内区半径取不同值时,考虑附加阻力影响,建立复合油藏直井井底压力动态如图 6所示。由图可知:内区无因次半径越大,内区径向流持续时间时间越长。在其他参数一定的情况下,内区无因次半径越大,压力波传播到内外区不连续边界的时间越长,内区径向流持续时间时间越长,外区拟径向流动阶段出现时间越晚。同时,受附加阻力影响,无因次压力及压力导数曲线上翘。
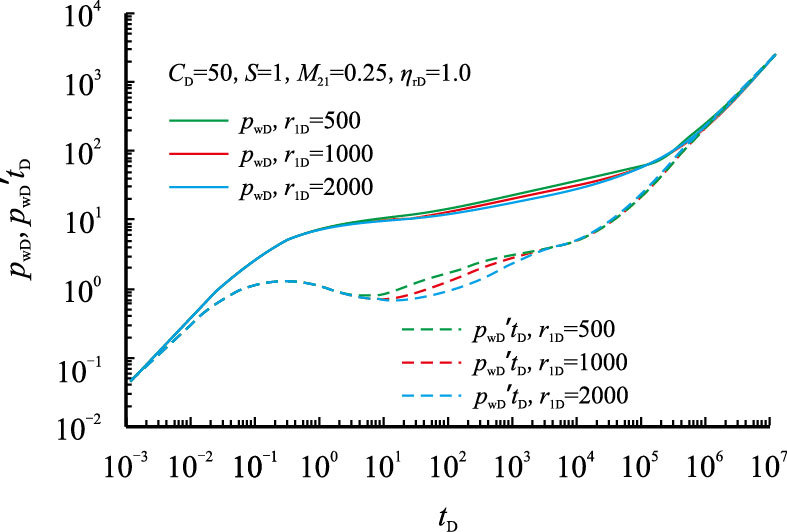 |
| 图6 内区无因次半径对压力动态的影响 Fig. 6 Type curves of well test affected by dimensionless radius of inner region |
当无因次导压系数取不同值时,考虑附加阻力影响,绘制复合油藏井底压力动态曲线如图 7所示。由图可知,导压系数值将影响内外区过渡段和外区径向流出现的时间,导压系数越小,内区储层压缩性越大,过渡段出现时间越早,且上抬幅度越大。
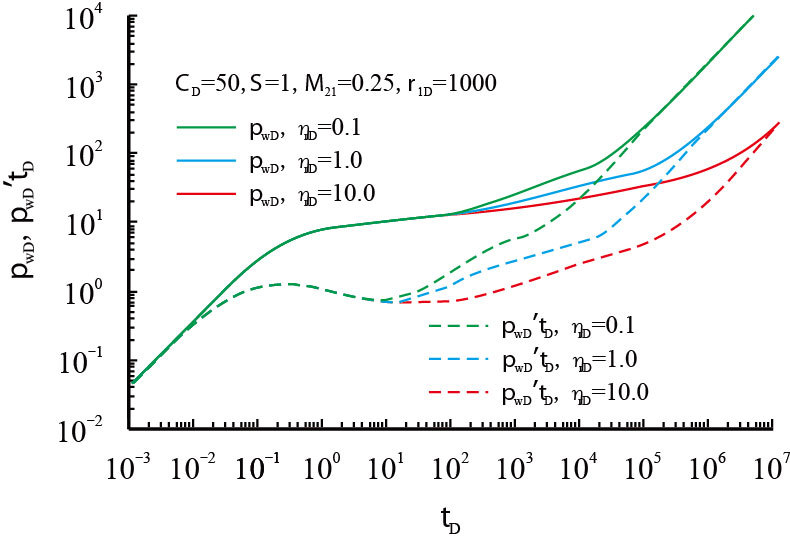 |
| 图7 无因次导压系数对压力动态的影响 Fig. 7 Type curves of well test affected by dimensionless pressure coefficient |
当内外区流度比$M_{21}$分别取1.00,0.25和5.00时,不考虑附加阻力影响,绘制考虑井筒储集和表皮效应的低渗透复合油藏完全压开直井的无因次井底压力动态曲线如图 8所示。
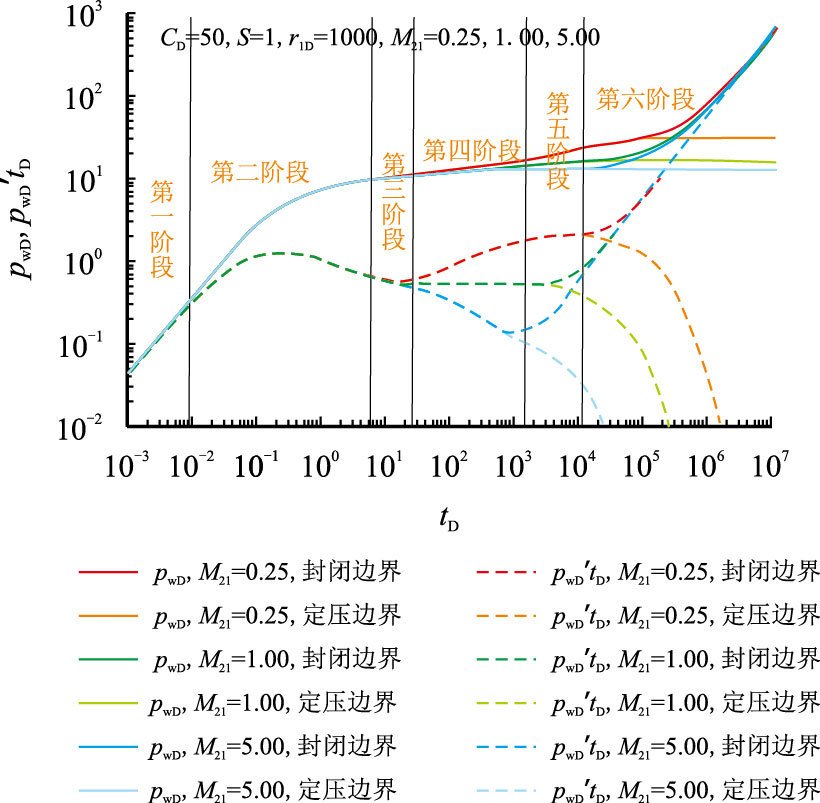 |
| 图8 内外区流度比对压力动态的影响 Fig. 8 Type curves of well test affected by mobility ratio |
由图 8可知,复合油藏直井渗流形态主要包括以下6个阶段:
(1) 早期纯井筒储集效应阶段,此阶段的压力和压力导数曲线重合,且为1条斜率为1.0的直线。
(2) 井筒储集效应与内区径向流动的过渡段,此阶段的压力导数曲线呈现向上凸起的“驼峰”,当储集系数和表皮因子较大时,可能掩盖内区径向流阶段。
(3) 内区径向流动阶段,此阶段的压力导数曲线与常规均质无限大储层中直井的线性相同,呈现一条水平直线。
(4) 内区径向流动阶段向外区径向流动阶段的过渡段,此阶段受$M_{21}$的影响,呈现出“上抬”,“下降”等形态。
(5) 外区径向流动阶段,压力导数呈现为一条水平直线,其值为$0.5M_{21}$。
(6) 外边界反映阶段,该阶段的主要特征是:当外边界为封闭边界时,压力和压力导数曲线上翘,呈斜率为1.0的直线;当为定压外边界时,压力导数在压力传到外边界后,迅速降为0。
3 结论(1) 考虑附加阻力梯度的影响,建立了满足低速非线性渗流规律的低渗透复合油藏数学模型,并采用有限元方法进行了数值求解。
(2) 通过与解析方法的结果对比,验证了有限元数值方法的正确性。并对内外区流度比、内区半径等参数对复合油藏井底压力动态的影响进行了敏感性分析。
(3) 低渗透油藏渗流附加阻力梯度使得无因次压力及压力导数曲线在径向流阶段上翘;通过与传统的拟启动压力梯度方法对比可知,拟启动压力梯度方法认为启动压力梯度为定值(最大附加阻力梯度值),存在动边界现象,将导致压力传播存在奇点,无因次压力及压力导数曲线上翘更厉害。
符号说明
${\phi_{\rm 1}}$—内区孔隙度,%;
${\phi_{\rm 2}}$—外区孔隙度,%;
${r_{\rm 1e}}$—内区半径,m;
${r_{\rm 2e}}$—外区半径,m;
h—储层厚度,m;
${q_{\rm o}}$—地面产量,m3/d;
t—时间,h;
v—渗流速度,cm/s;
$\beta$—单位转换系数,无因次,取$\beta$=0.01;
$\lambda$—流度,mD/mPa$\cdot$s;
p—压力,MPa;
$G_{\rm m}$—拟启动压力梯度,MPa/cm;
G—附加阻力梯度,MPa/cm;
a,b,c—回归系数,无因次;
$R^2$—回归相关系数,无因次;
$G_0$—启动压力梯度值,MPa/cm;
$p_{\rm m}$—最大拟启动压力梯度对应的驱替压力,MPa;
${r_{\rm we}}$—有效井半径,m;
${r_{\rm w}}$—井半径,m;
${s}$—表皮系数,无因次;
${t_{\rm D}}$—无因次时间;
${c_{\rm t1}}$—内区储层原始压缩系数,MPa$^{-1}$;
${c_{\rm t2}}$—外区储层原始压缩系数,MPa$^{-1}$;;
${r_{\rm 1D}}$—无因次内区半径;
${r_{\rm 2D}}$—无因次外区半径;
${M_{\rm 21}}$—内外区流度比,无因次;
${\eta_{\rm rD}}$—内外区导压系数比,无因次;
$\lambda_1$—内区流体流度,mD/mPa$\cdot$s;
$\lambda_2$—外区流体流度,mD/mPa$\cdot$s;
${G_{\rm D}}$—无因次启动压力梯度;
${C_{\rm D}}$—无因次井筒储集系数;
${p_{\rm D}}$—无因次压力;
${G_{\rm 1D}}$,${G_{\rm 2D}}$—无因次内区/外区启动压力梯度;
${p_{\rm 1D}}$,${p_{\rm 2D}}$—无因次内区/外区压力;
B—体积系数,无因次;
C—井筒储集系数,m3/MPa;
${p_{\rm i}}$—原始地层压力,MPa;
r—半径,m;
${r_{\rm D}}$—无因次半径;
${p_{\rm wD}}$—无因次井底压力;
${r_{\rm eD}}$—无因次泄油半径;
n—边界法向;
$N_l$—插值函数,无因次;
$\Omega$—积分区域;
i,j,k—节点编号;
$a_l$,$b_l$,$c_l(l =i,j,k)$—插值函数系数,无因次;
$x_l$,$y_l(l =i,j,k)$—三角形单元顶点坐标,m;
${v_{\rm tD}}$—无因次速度;
$S_{ij}$—单元中$ij$边的无因次长度。
| [1] | OLAREWAJU J S, LEE W J. A comprehensive application of a composite reservoir model to pressure transient analysis[J]. SPE Reservoir Engineering, 1989, 3 (4) : 325 –331. |
| [2] | KUCHUK F J, HABASHY T M. Solution of pressure diffusion in radially composite reservoirs[J]. Transport in Porous Media, 1995, 19 (3) : 199 –232. DOI:10.1007/BF00617530 |
| [3] | FENG J, LUO R, CHENG L, et al. A Composite Seepage Model for Fractured Reservoir[C]//SPE Middle East Oil and Gas Show and Conference, Society of Petroleum Engineers, 2009. |
| [4] |
宁正福, 廖新维, 高旺来, 等. 应力敏感裂缝性双区复合气藏压力动态特征[J].
大庆石油学院学报, 2004, 28 (2) : 34 –36.
NING Zhengfu, LIAO Xinwei, GAO Wanglai, et al. Pressure transient response in deep-seated geothermal stresssensitive fissured composite gas reservoir[J]. Journal of Daqing Petroleum Institute, 2004, 28 (2) : 34 –36. |
| [5] |
刘启国, 冯宇, 董凤玲, 等. 受界面附加阻力影响的双重介质径向复合油藏试井解释模型研究[J].
油气井测试, 2005, 14 (3) : 11 –13.
LIU Qiguo, FENG Yu, DONG Fengling, et al. Study on testing interpretation model of dual medium and radial compound reservoir influenced by interface addition friction[J]. Well Testing, 2005, 14 (3) : 11 –13. |
| [6] |
李汝勇, 孙文涛, 李顺初, 等. 双孔介质复合封闭储层压力分布的求解分析[J].
钻采工艺, 2007, 30 (1) : 54 –56.
LI Ruyong, SUN Wentao, LI Shunchu, et al. Solution analysis of pressure distribution in composite bounded reservoir with two porous-media[J]. Drilling & Production Technology, 2007, 30 (1) : 54 –56. |
| [7] | SUN Q Y, ZHANG R L, ZHANG Y Z, et al. Pressure transient analysis of the low permeability composite reservoir with threshold pressure gradient[C]//Power and Energy Engineering Conference. IEEE, 2010:1-4. |
| [8] | LU J, GHEDAN S. Pressure behavior of vertical wells in low-permeability reservoirs with threshold pressure gradient[J]. Special Topics & Reviews in Porous Media, 2011, 2 (3) : 157 –169. |
| [9] |
程时清, 张盛宗, 黄延章, 等. 低速非达西渗流动边界问题的积分解[J].
力学与实践, 2002, 24 (3) : 15 –17.
CHENG Shiqing, ZHANG Shengzong, HUANG Yanzhang, et al. An integral solution of free-boundary problem of non-Darcy flow behavior[J]. Mechanics in Engineering, 2002, 24 (3) : 15 –17. |
| [10] |
王晓冬, 侯晓春, 郝明强, 等. 低渗透介质有启动压力梯度的不稳态压力分析[J].
石油学报, 2011, 32 (5) : 847 –851.
WANG Xiaodong, HOU Xiaochun, HAO Mingqiang, et al. Pressure transient analysis in low-permeable media with threshold gradients[J]. Acta Petrolei Sinica, 2011, 32 (5) : 847 –851. |
| [11] |
方甲中, 程林松, 任胜利, 等. 动边界复合油藏低速非达西渗流试井分析[J].
西南石油大学学报(自然科学版), 2011, 33 (5) : 104 –108.
FANG Jiazhong, CHENG Linsong, REN Shengli, et al. Well test analysis of low velocity and non-Darcy flow incomposite reservoir with dynamic boundary[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33 (5) : 104 –108. |
| [12] |
李传亮. 动边界其实并不存在[J].
岩性油气藏, 2010, 22 (3) : 121 –123.
LI Chuanliang. Moving bounary does not truly exist[J]. Litholigic Reservoirs, 2010, 22 (3) : 121 –123. |
| [13] | GUO J, LI Y, ZHAO J, et al. The application of boundary element method to pressure behaviour analysis in a composite reservoir with lateral drilling[J]. Journal of Canadian Petroleum Technology, 2004, 43 (7) : 38 –44. |
| [14] |
程林松, 任胜利, 廉培庆. 动边界双重介质油藏低速非达西渗流试井模型[J].
计算力学学报, 2011, 28 (6) : 879 –883.
CHENG Linsong, REN Shengli, LIAN Peiqing. Well test analysis on low velocity and non-Darcy flow in dual-porosity reservoir with dynamic boundary[J]. Chinese Journal of Computational Mechanics, 2011, 28 (6) : 879 –883. |
| [15] |
LIU Zhenyu. The theory and application of finite element method for the flow in reservoir[D]. Daqing:Daqing Petroleum Institute, 2003.
刘振宇. 有限元法在油藏渗流中的理论和应用[D]. 大庆:大庆石油学院, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10220-2004050751.htm |
| [16] |
朱维耀, 刘今子, 宋洪庆, 等. 低/特低渗透油藏非达西渗流有效动用计算方法[J].
石油学报, 2010, 31 (3) : 452 –457.
ZHU Weiyao, LIU Jinzi, SONG Hongqing, et al. Calculation of effective startup degree of non-Darcy flow in low or ultra-low permeability reservoirs[J]. Acta Petrolei Sinica, 2010, 31 (3) : 452 –457. |
| [17] |
闫栋栋, 杨满平, 王刚, 等. 低流度油藏启动压力梯度分析[J].
大庆石油学院学报, 2010, 34 (1) : 39 –42.
YAN Dongdong, YANG Manping, WANG Gang, et al. Threshold pressure gradient analysis for low mobility reservoir[J]. Journal of Daqing Petroleum Institute, 2010, 34 (1) : 39 –42. |
| [18] |
许建红, 程林松, 周颖. 一种求解低渗透油藏启动压力梯度的新方法[J].
石油勘探与开发, 2007, 34 (5) : 594 –597.
XU Jianhong, CHENG Linsong, ZHOU Ying. A new method for calculating kickoff pressure gradient in low permeability reservoirs[J]. Petroleum Exploration and Development, 2007, 34 (5) : 594 –597. |
| [19] |
张烈辉.
油气藏数值模拟基本原理[M]. 北京: 石油工业出版社, 2005 .
ZHANG Liehui. Basic principles of numerical simulation of oil and gas reservoirs[M]. Bejing: Petroleum Industry Press, 2005 . |
 2016, Vol. 38
2016, Vol. 38


