2. 中国石油新疆油田公司勘探开发研究院, 新疆 克拉玛依 834000;
3. 中国石油川庆钻探工程有限公司井下作业公司, 四川 成都 610051
2. Exploration and Development Research Institute of Xinjiang Oilfield Company, PetroChina, Karamay, Xinjiang 834000, China;
3. Chuanqing Drilling Engineering Company Limited Downhole Service Company, PetroChina, Chengdu, Sichuan 610051, China
基质酸化是解除碳酸盐岩近井筒地带污染、降低近井筒地带渗流阻力的一种增产手段。碳酸盐岩基质酸化过程会在近井筒地带形成酸蚀蚓孔[1],酸液体系、施工参数、岩石类型和储层条件从机理上决定了蚓孔特征参数的大小(蚓孔长度、蚓孔半径) [2],进而影响酸化效果。常用的酸化增产倍比法[1, 3] 未考虑这些蚓孔特征参数对产能的影响,本文基于蚓孔生长机理,推导了描述蚓孔特征参数新模型,建立了酸蚀蚓孔区等效渗透率模型和产能模型,依据实验数据优选出蚓孔突破岩芯时酸液注入的最优孔隙体积倍数与最优注酸速度,预测了基质酸化产能,与真实定压产能相近,为优化碳酸盐岩基质酸化产能提供了可靠途径。
1 新模型研究 1.1 蚓孔扩展模型碳酸盐岩基质酸化作业中酸蚀蚓孔扩展过程的数学模型大致可以分为4 大类[4]:(1)无因次模型;(2)毛细管模型;(3)网络模型;(4)连续模型。这些模型可在理想条件下(岩芯线性流、单一主蚓孔、指定浓度的盐酸体系)预测酸蚀蚓孔的增长,但在复杂的基质酸化过程(径向流、多蚓孔、复杂酸液体系)中则表现不足[5]。Buijse M A 和Glasbergen G[5]认为蚓孔生长速度只与突破岩芯时的酸液体积有关,取决于注酸速度和蚓孔尖端处酸液流速,且表现为离井筒越远,增长速度越慢,并推导了径向蚓孔生长速度的半经验关系式,表述为
| ${{\upsilon }_{\text{wh}}}=\frac{{{\upsilon }_{\text{i}}}}{{{V}_{\text{bt},\text{opt}}}}\times {{\left( \frac{{{\upsilon }_{\text{i}}}}{{{\upsilon }_{\text{i},\text{opt}}}} \right)}^{-1/3}}\times {{\left[ 1-{{\text{e}}^{-4{{\left( \frac{{{\upsilon }_{\text{i}}}}{{{\upsilon }_{\text{i},\text{opt}}}} \right)}^{2}}}} \right]}^{2}}$ | (1) |
式中:
$\upsilon _{{\rm{wh}}}$-蚓孔生长速度,m/s;
$\upsilon _{\rm{i}}$-岩石孔隙内酸液流速,m/s;
$\upsilon _{{\rm{i,opt}}}$-岩石孔隙内酸液最优流速,m/s;
$V_{{\rm{bt,opt}}} $-蚓孔突破岩芯时酸液注入的最优孔隙体积倍数,无因次。
取时间的微元段,在Δt 时间内,蚓孔生长速度视为一个常数,蚓孔径向等效长度可表述为
| $\left( {r_{\rm{{wh}} } } \right)_{n + 1} = \left( {r_{\rm{wh} } } \right)_n + \upsilon _{{\rm{wh}}} \Delta t$ | (2) |
岩石孔隙内酸液流速$\upsilon _{\rm{i}}$可由Furui K 等[6] 推导的岩石孔隙内酸液流速计算公式计算,表述为
| $\upsilon _{\rm{i}} = \dfrac{{d_{{\rm{e,wh}}} }}{{d_{{\rm{core}}} }}\upsilon _{{\rm{i,tip}}}$ | (3) |
式中:
$d_{{\rm{e,wh}}}$-等效蚓孔直径,m;
$d_{{\rm{core}}} $-室内实验岩芯直径,m;
$\upsilon _{{\rm{i,tip}}}$-蚓孔尖端处酸液流速,m/s。
酸液径向流蚓孔尖端处流速和等效蚓孔直径的计算公式可分别表述为[6-7]
| $\upsilon _{{\rm{i,tip}}} = \dfrac{q}{{2\pi h\phi \sqrt {d_{{\rm{e,wh}}} r_{{\rm{wh}}} } }}$ | (4) |
| $d_{{\rm{e,wh}}} = d_{{\rm{core}}} N_{{\rm{ac}}} V_{{\rm{bt,opt}}}$ | (5) |
式中:
q-酸液排量,m3/s;
h-储层厚度,m;
$\phi$-孔隙度,无因次;
$r_{{\rm{wh}}}$-蚓孔径向等效长度,m。
酸溶解能力$N_{\rm{ac}}$定义为
| $N_{{\rm{ac}}} = \dfrac{{\phi \beta C_0 \rho _{{\rm{acid}}} }}{{\left( {1 - \phi } \right)\rho _{{\rm{rock}}} }}$ | (6) |
式中:
$\beta$-酸液溶解能力系数,kg/kg;
$C_0$-酸液浓度,%;
$\rho_{\rm{acid}}$-酸液密度,kg/m3;
$\rho_{\rm{rock}}$-岩石密度,kg/m3。
依据式(1)∼ 式(6)可计算碳酸盐岩基质酸化过程中蚓孔径向扩展的等效长度和等效直径。
1.2 蚓孔区等效渗透率模型碳酸盐岩酸化后,会在近井筒地带形成高速渗流通道的蚓孔区(图 1),表现为高孔隙度和高渗透率。射孔完井情况下,酸液通过射孔孔眼进入地层,形成的酸蚀主蚓孔数与射孔孔眼数相同。根据平面径向流的等效渗流阻力原理[8],推导出酸蚀蚓孔区等效渗透率¯K 的计算公式,简化为
| $\bar K = \dfrac{{md_{{\rm{e,wh}}} K_{{\rm{wh}}} + \left( {h - md_{{\rm{e,wh}}} } \right)K_0 }}{h}$ | (7) |
式中:
m-射孔孔眼(酸蚀主蚓孔)总数,个;
$K_0$-基质渗透率,mD;
$K_{{\rm{wh}}}$-蚓孔等效渗透率,mD。
 |
| 图1 近井筒地带基质酸化等效主蚓孔形成示意图 Fig. 1 Schematic of matrix acidizing dominant wormhole innear wellbore |
国外学者[9-13] 把蚓孔生长简化成具有一定等效半径和等效长度的毛细管的扩展过程,并忽略蚓孔迂曲度的影响。李传亮等[14] 推导出管流与渗流条件下渗透率的统一表达式,即酸蚀蚓孔等效渗透率的计算公式为
| $K_{{\rm{wh}}} = \dfrac{{d_{{\rm{e,wh}}}^2 }}{{32}}$ | (8) |
根据等效渗流阻力原理和平面径向稳定渗流达西定律,可得酸蚀蚓孔区和无蚓孔区的压降。
酸蚀蚓孔区的压降
| $\Delta p_1 = \dfrac{{BQ\mu \ln \left( {{{r_{{\rm{wh}}} } /{r_{\rm{w}} }}} \right)}}{{2\pi \bar Kh}}$ | (9) |
无蚓孔区的压降
| $\Delta p_2 = \dfrac{{BQ\mu \ln \left( {{{r_{\rm{e}} } / {r_{{\rm{wh}}} }}} \right)}}{{2\pi K_0 h}}$ | (10) |
由于该渗流过程为串联模式,故$p_{\rm{e}} - p_{{\rm{wf}}} = \Delta p_1 + \Delta p_2 $,代入各段压差,整理得
| $Q = \dfrac{{2\pi h\left( {p_{\rm{e}} - p_{{\rm{wf}}} } \right)}}{{B\mu \left( {\dfrac{1}{{\bar K}}\ln \dfrac{{r_{{\rm{wh}}} }}{{r_{\rm{w}} }} + \dfrac{1}{{K_0 }}\ln \dfrac{{r_{\rm{e}} }}{{r_{{\rm{wh}}} }}} \right)}}$ | (11) |
式中:
Q-产能,m3/d;
$p_{\rm{e}}$-原始地层压力,MPa;
$p_{\rm{wf}}$-井底流压,MPa;
$\mu$-原油黏度,mPa$\cdot$s;
$r_{\rm{e}}$-泄油半径,m;
$r_{\rm{w}}$-井筒半径,m;
B-地层原油体积系数,m3/m3。
2 模型应用某一碳酸盐岩(主要为方解石)油藏完善生产井,定井底流压生产,原始地层压力$p_{\rm{e}}$为24.21~MPa,井底流压$p_{\rm{wf}}$为21.37 MPa,地层平均孔隙度$\phi$为0.08,地层平均原始渗透率$K_0$ 为3.34 mD,地层原油黏度$\mu$为5.2 mPa$\cdot$s,地层温度78.2 ℃,生产井井筒半径$r_{\rm{w}}$为0.1 m,泄油半径$r_{\rm{e}}$为147.5 m,储层厚度h为8.52 m,射孔密度为16 孔/m,地层原油体积系数B 为1.08 m3/m3,改造前该油井产量为1.48 m3/d。
采用15%HCl 进行基质酸化改造措施,施工排量为0.5 m3/min,盐酸注入体积为12 m3,改造后定压差生产,产量为19.89 m3/d。
2.1 蚓孔参数求解取多块岩芯进行室内酸化驱替实验,实验参数见表 1。改变驱替泵的注酸速度,获取对应条件下蚓孔突破时酸液注入的孔隙体积倍数,绘制蚓孔突破时酸液注入的孔隙体积倍数与注入速度关系曲线(图 2),优选出最优孔隙体积倍数$V_{{\rm{bt,opt}}}$为1.89,最优注入速度为0.70 cm/min。
| 表1 基质酸化室内驱替实验参数(实验温度78.2 °C) Table 1 Matrix acidizing laboratory displacement experimental parameters(78.2 °C) |
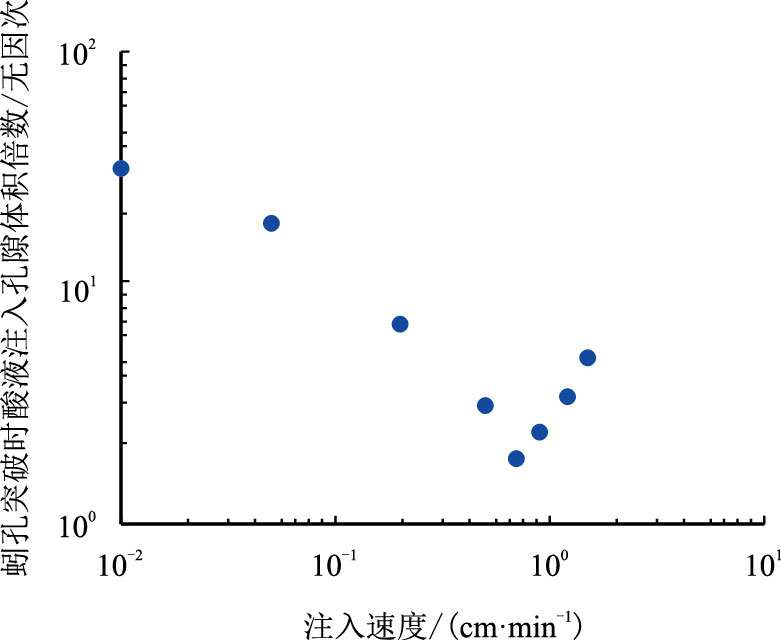 |
| 图2 蚓孔突破时酸液注入的孔隙体积倍数与注入速度关系 Fig. 2 Pore volumes to breakthrough vs. injection rate by core flow test results |
查取资料知:15%盐酸密度$\rho_{\rm{acid}}$为1 072 kg/m3,方解石岩石密度$\rho_{\rm{rock}}$为2 710 kg/m3,分别计算3个基础参数。
纯盐酸对方解石的溶解能力系数
| $\beta = \dfrac{{100.09 \times 1}}{{36.47 \times 2}} = 1.26~{\rm{kg/kg}}$ |
酸溶解能力$N_{\rm{ac}}$
| $N_{{\rm{ac}}} = \dfrac{{\phi \beta C_0 \rho _{{\rm{acid}}} }}{{\left( {1 - \phi } \right)\rho _{{\rm{rock}}} }} = \dfrac{{0.08 \times 1.26 \times 0.15 \times 1072}}{{2710 \times \left( {1 - 0.08} \right)}} = \hspace{3em}1.08 \times 10^{ - 3}$ |
酸蚀蚓孔等效直径
| $d_{{\rm{e,wh}}} = 0.0254 \times 1.08 \times 10^{ - 3} \times 1.89 = 5.19 \times 10^{ - 3}~ {\rm{cm}}$ |
本文假定$t=0$时,$r_{{\rm{wh}}} = r_{\rm{w}} $,取时间间隔$\Delta t$=1 s,由式(1)~式(4)计算出等效蚓孔长度随注入时间的变化关系(图 3),从图 3 中可知,泵入12 m3 盐酸返排后所获得的等效蚓孔长度为1.81 m。
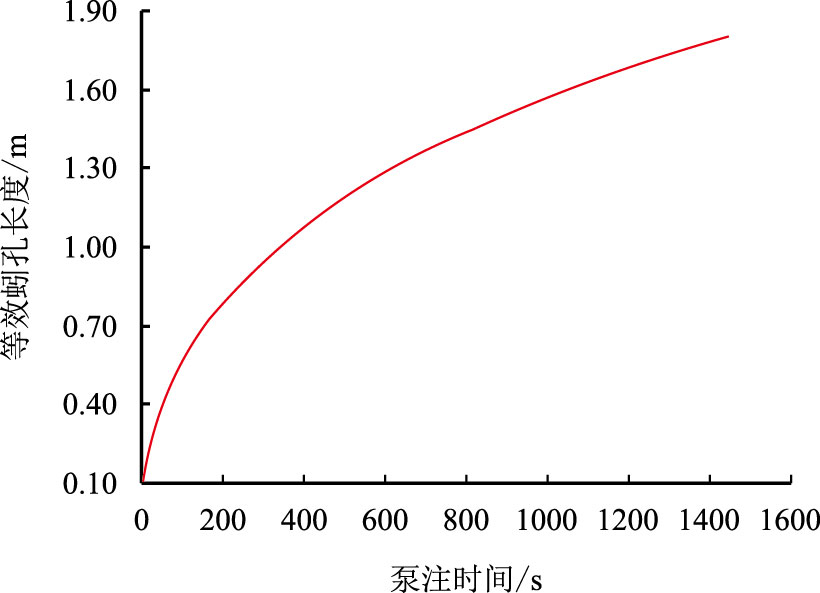 |
| 图3 等效蚓孔长度随注入时间的变化预测趋势 Fig. 3 Equivalent wormhole length vs. injection time |
由射孔密度和储层厚度计算得到射孔孔眼数为136 个,即酸化施工后获得的主蚓孔数m也为136 个。根据蚓孔区等效渗透率模型的计算公式(8)计算得到等效单个主蚓孔渗透率为84 235.56 mD,由公式(7)计算得到蚓孔区等效渗透率为3 493.84 mD。
由产能模型计算公式(11)计算改造后获得的油井产量为20.51 m3/d,与改造后定压差生产的真实产量,增产倍比为13.44。
3 结论(1)基于径向蚓孔扩展模型和等效渗透率模型建立了碳酸盐岩基质酸化产能预测新模型,为产能预测提供了一种理论依据。
(2)依据蚓孔突破时酸液注入的孔隙体积倍数与注入速度实验数据,优选出蚓孔突破岩芯时酸液注入的最优孔隙体积倍数为1.89,最优注酸速度为0.7 cm/min。
(3)结合酸化施工井层实例,预测了改造后的产能为20.51 m3/d,与真实求产产能19.89 m3/d 相当,增产倍比为13.44。
| [1] | 李颖川. 采油工程[M]. 北京: 石油工业出版社, 2009 . |
| [2] | 张保平, 蒋阗, 刘立云, 等. 油藏增产措施[M]. 北京: 石油工业出版社, 2002 . |
| [3] | 万仁溥, 罗英俊. 采油技术手册(修订本),第九分册:压裂酸化工艺技术[M]. 北京: 石油工业出版社, 1997 . |
| [4] | MAHESHWARI P, RATNAKAR R R, KALIA N, et al. 3-D simulation and analysis of reactive dissolution and wormhole formation in carbonate rocks[J]. Chemical Engineering Science, 2013, 90 : 258 –274. DOI:10.1016/j.ces.2012.12.032 |
| [5] | BUIJSE M A, GLASBERGEN G. A semi-empirical model to calculate wormhole growth in carbonate acidizing[C]. SPE 96892, 2005. |
| [6] | FURUI K, BURTON R C, BURKHEAD D W, et al. A comprehensive model of high-rate matrix acid stimulation for long horizontal wells in carbonate reservoirs part i-scaling up core-level acid wormholing to field treatments[C]. SPE 134265, 2012. |
| [7] | ECONOMIDES M J, HILL A D, ECONOMIDES E C, et al. Petroleum production systems[M]. Second Edition, Pearson Education, Inc. U.S.A, 2013 . |
| [8] | 何更生, 唐海. 油层物理[M]. 北京: 石油工业出版社, 2011 . |
| [9] | SCHECHTER R S, GIDLEY J L. The change in pore size distribution from surface reactions in porous media[J]. AIChE Journal, 1969, 15 (3) : 339 –350. DOI:10.1002/(ISSN)1547-5905 |
| [10] | HUNG K M, HILL A D, SEPEHRNOORI K. A mechanistic model of wormhole growth in carbonate matrix acidizing and acid fracturing[J]. Journal of Petroleum Technology, 1989, 41 (1) : 59 –66. DOI:10.2118/16886-PA |
| [11] | GDANSKI R. A fundamentally new model of acid wormholing in carbonates[C]. SPE 54719, 1999. |
| [12] | GONG M, EL-RABAA A M. Quantitative model of wormholing process in carbonate acidizing[C]. SPE 52165, 1999. |
| [13] | BUIJSE M A. Understanding wormholing mechanisms can improve acid treatments in carbonate formations[C]. SPE 65068, 2000. |
| [14] |
李传亮, 张学磊. 管流与渗流的统一[J].
新疆石油地质, 2007, 28 (2) : 252 –253.
LI Chuanliang, ZHANG Xuelei. Unification of flow equations in tubes and in porous media[J]. Xinjiang Petroleum Geology, 2007, 28 (2) : 252 –253. |
 2016, Vol. 38
2016, Vol. 38


