2. 中海油研究总院, 北京 朝阳 100028
2. CNOOC Research Institute, Chaoyang, Beijing 100028, China
随着油气勘探的不断发展和深入,中国很多油田已经进入隐蔽油气藏勘探开发时期,隐蔽油气藏具有隐蔽性强、不易识别、相变快、非均质强、单砂体厚度薄以及成藏条件复杂等特点。地震反演技术在寻找复杂油气藏、搞清砂体分布规律、研究油气水关系以及开展砂体描述等方面具有重要作用,是为井网部署和井位优化提供主要依据的关键技术[1]。由于受到有限带宽度以及方法本身的限制,常规反演方法的结果无法识别薄互层沉积。地质统计学是属于随机地震约束储层建模一类方法,在非均质性储层建模、地质储量计算等方面有着重要的应用[2-7]。地质统计学反演是将地质统计学与常规反演相结合的反演技术[8],但是该技术受到计算机硬件要求和算法本身复杂性的影响,发展较缓慢。近年来,随着计算机技术的快速发展,该方法越来越多地应用于储层预测、参数分析和非均质性研究等方面[9]。
目前较为成熟的地质统计学反演方法是基于序贯高斯模拟的地质统计学反演方法。对于多个波阻抗的实现,尽管实现各不相同,但每次实现都满足两个条件:在井点上与测井数据计算的波阻抗一致;在井间,符合地震数据和已知数据的地质统计学特征。Hass A 等将该方法用于约束三维地震数据的储层预测[10]。不少学者将该技术应用于不同工区的薄砂层划分[11-14],精细地描述了有效储集层物性在反演剖面上的空间展布形态,均取得了较好的应用效果。尚建林等还实现了多种测井参数的反演[15],有效减小了单一参数预测的风险,为陆相砂泥岩薄互层预测提供了新的途径。但该类技术仍然不能很好地解决多解性和不确定性问题。
本文通过引入贝叶斯后验概率公式和马尔科夫链蒙特卡洛算法、结合随机模拟理论与地震反演,形成一套充分考虑地震、测井、地质信息不确定性共同约束的储层空间预测技术,称为概率法反演技术。该技术是地质统计学反演技术的发展,继承了地质统计学反演的所有优点,并将储层的确定性描述转向不确定描述,可以有效提高地震资料识别储层的分辨率。由于综合了地震反演和储层建模的优势,该技术具有地震数据横向密集、测井数据垂向密集、储层描述概率性的特点,可以作为薄砂体储层识别的有效方法。
1 概率法反演技术 1.1 基本原理概率法反演技术本质上是一种充分考虑地震、测井、地质信息不确定性共同约束的储层空间预测技术(图 1)。它的核心思想是利用贝叶斯后验概率[16-17] 公式将地震、测井、地质的不确定性转换为后验概率分布,并利用马尔科夫链从后验概率中抽取随机样本,最后利用蒙特卡洛算法计算随机样本的期望,并把最优的期望值,作为空间中储层的解。
 |
| 图1 概率法反演示意图 Fig. 1 Sketch map of the probability inversion technique |
贝叶斯后验概率与马尔科夫链蒙特卡洛算法是概率法反演的核心技术。假设事件A 只能与两两互不相容事件$H_1$,$H_1$,$\cdots$,$H_n$之一同时发生,且有$\sum\limits_{i = 1}^n {{{H}_i} = \Omega } $($\Omega$为样本空间),则A发生后,$H_i$再发生的概率为
| $P(H_{i}|A) = \dfrac{{P({{H}_i})P({A}|{{H}_i})}}{{\sum\limits_{i = 1}^n {P({{H}_i})P({A}|{{H}_i})} }} $ | (1) |
式中:$P({H}_{i}|{A})$ 贝叶斯后验概率,它反映了试验后待估量发生的可能性。
对于马尔科夫链—蒙特卡洛算法,是利用蒙特卡洛算法估计积分$\int_A {g(t)\textrm{d}t} $。它将积分表示成对某个概率$f(t)$下的期望。从而积分问题转化为利用马尔科夫链从目标概率密度$f(t)$中抽取随机样本。假定样本$x = ({x_1}, \cdots ,{x_n})$和参数$\theta $的联合分布可表示为
| ${f_{x,\theta }}(x,\theta ) = {f_{x|\theta }}({x_1}, \cdots ,{x_n})\pi (\theta ) $ | (2) |
根据贝叶斯后验概率公式,可利用样本 $x = ({x_1}, \cdots ,{x_n})$对$\theta $的分布更新,得到后验概率${f_{\theta |x}}(\theta |x)$。定义积分的蒙特卡洛估计为样本均值
| $\overline g = \sum\limits_{i = 1}^N {{x_i}/N} $ | (3) |
式中:$x_1$,$x_2$,$\cdots$,$x_n$—从马尔科夫链构造的平稳分布${f_{\theta |x}}(\theta |x)$中抽取的随机样本。当$x_1$,$x_2$,$\cdots$,$x_n$独立时,由大数定律知,当样本量n趋于无穷时,$\overline g $收敛到$g(\theta )$的期望$Eg(\theta |x)$。
1.2 技术流程概率法反演的技术流程如图 2 所示。(1)在精细标定和框架模型的约束下,结合岩石物理分析,通过对研究区约束稀疏脉冲反演结果的研究,获得各小层横向变程和地震权重;(2)利用测井曲线求取各小层不同岩性的含量、概率密度函数、纵向变程;(3)将上述获得的参数作为输入数据,开展蒙特卡洛概率法反演,得到多个等概率的岩性体和阻抗体实现;(4)通过对多个等概率的岩性、阻抗、物性实现的统计分析,得到岩性概率体、P10/P50/P90 概率体、阻抗综合分析体和物性综合分析体等。其中,岩性概率体实现了储层描述由确定性向不确定性的转变,将空间中某区域为某种岩性的描述转为某种岩性可能性的大小,这种带有概率思想的描述,更符合地质沉积规律。另外,利用云变换将多个等概率的岩性体和阻抗体转换为多个等概率的物性体实现,对储层属性地质建模具有重要意义。
 |
| 图2 概率法反演技术流程 Fig. 2 Probability inversion technical workflow |
采用 “五步法”进行井震标定,即标志层的标定、精细标定、提取全井子波、精细地层格架约束下修正标定,重新提取全井子波、利用新全井子波修正合成地震记录,进行标定的精细修正。① 标志层是指在油田区域可追踪对比的地震反射层,一般指油组,标准层的标定就是进行油组的井震标定。② 精细标定主要是建立油组内部砂层组的井震关系,通过适当修正合成地震记录,标定油组内各小层、砂层组。③ 提取全井子波时,需剔除形态异常的子波((图 3 标注框内蓝色子波),子波估计时窗一般为3倍以上子波长度,以保证为子波对称。采用全井子波而非平均子波可保证提取的子波具有更高的精度,更符合实际。④ 精细地层格架约束,可保证合成地震记录的产状与格架产状一致,提高标定精度(图 4)。° 利用精细地层格架约束下提取的全井子波合成地震记录,进行标定的精细修正。
 |
| 图3 全井子波提取 Fig. 3 Extracted wavelet |
 |
| 图4 常规标定与地层格架约束标定对比图 Fig. 4 Comparison between Conventional calibration and calibration controlled by framework |
地层格架的精度,直接影响概率法反演的分辨率。常规方法搭建的格架,在地层接触关系复杂(图 5a)时,断层位置处地层产状易发生畸变(图 5b)。为确保反演结果的精度,采用EarthModel FT 搭建格架。其搭建的格架在地层接触关系复杂时,产状清晰(图 5c)。
 |
| 图5 地层格架示意图 Fig. 5 Sketch map of the stratigraphic framework |
概率密度函数用于描述某一属性值在空间中的分布情况。为确保反演结果的精度,利用约束稀疏脉冲反演对储层形态与展布特征的认识,给出理论概率密度函数,可有效避免井曲线样点过少导致概率密度函数不平滑,从而出现跳跃点,在反演中引入人为噪音(图 6)。
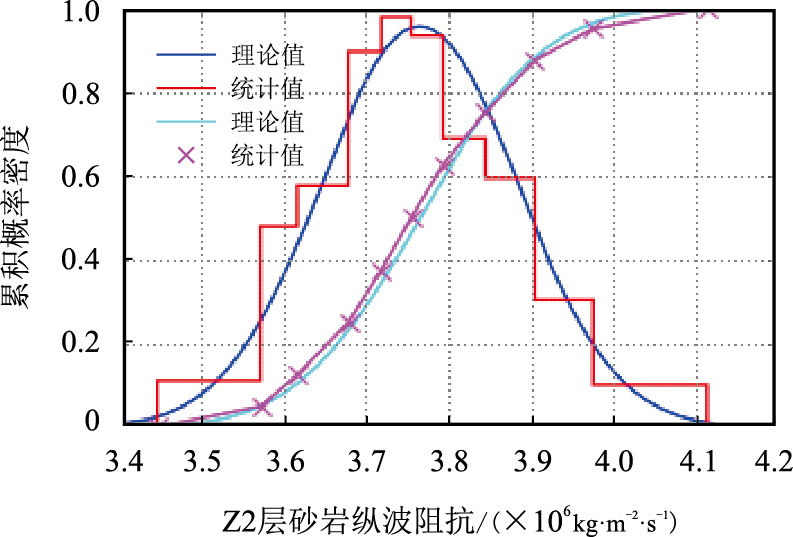 |
| 图6 理论概率密度函数与样点统计概率密度函数 Fig. 6 The probability density function in theory and the probability density function of sample points |
变程主要用于描述空间中两点间的差异情况。垂向变程由各项同性条件下测井曲线统计得到(图 7)。横向变程则由约束稀疏脉冲反演得到的岩性体、物性体及平面属性综合分析得到(图 8)。概率法反演中,垂向变程对反演结果分辨率的影响较大,横向变程影响相对较小,但需确保主次方向大小一致,横向的趋势主要由地震约束。
 |
| 图7 垂向变程统计 Fig. 7 The vertical range |
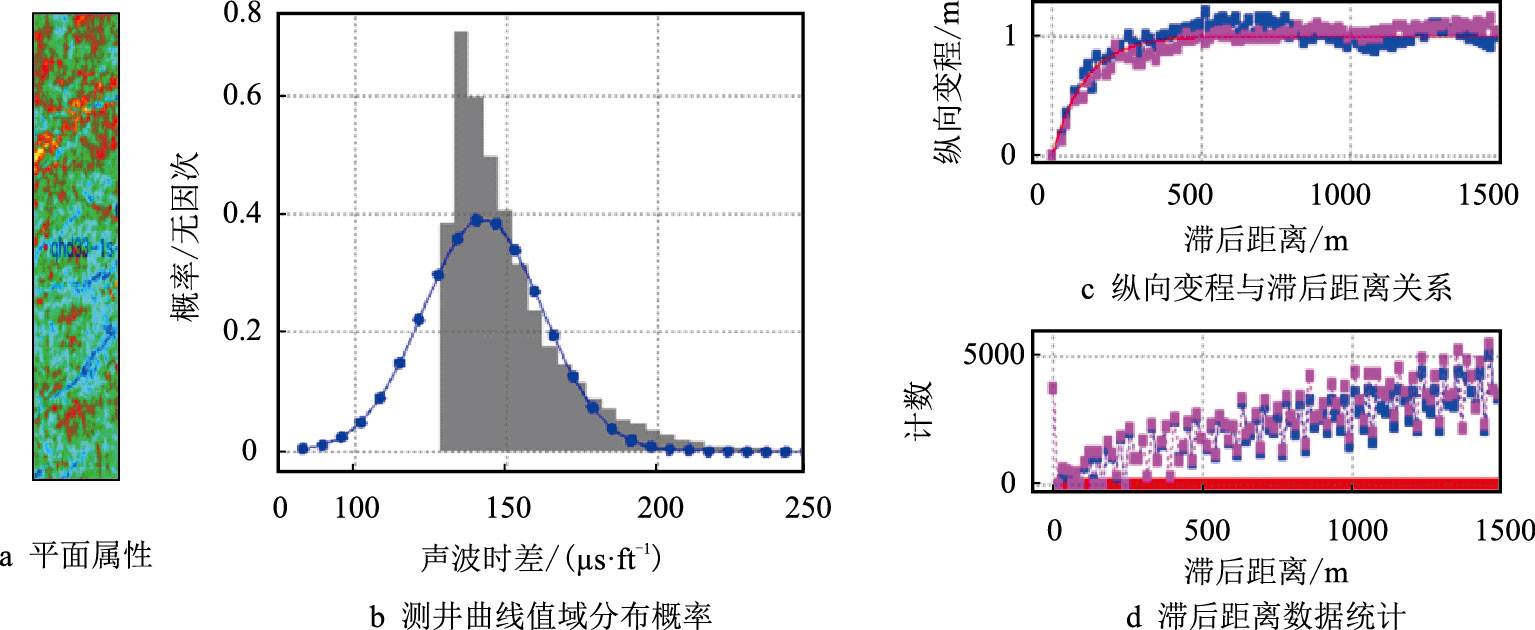 |
| 图8 横向变程统计 Fig. 8 The lateral range |
概率法反演技术主要有3 个方面的优点:(1)垂向分辨率高[18-23],细节信息更丰富;(2)多次等概率实现,可有效降低地震反演的多解性;(3)地震硬约束,确定横向趋势,可有效降低井间插值正演井上分辨率高,井间不可靠的缺陷。
图 9 为约束稀疏脉冲反演与概率法反演波阻抗对比图。对比图中标注区域可知,约束稀疏脉冲反演由于垂向分辨率较低,井上多期砂体间的叠置关系模糊;由于概率法反演结合了井上分辨率高的特点,各期砂体间叠置关系清晰,细节信息更丰富。图 10 为井间插值正演与地震约束正演确定的横向趋势效果对比图。图中黑色波形为地震,红色波形为正演结果。对比图 10a、图 10b,井间插值结果垂向分辨率高,但是井间的地震波形与正演结果差距大;对于地震约束下,井间的地震波形与正演结果匹配好,这说明地震硬约束确定的横向趋势可有效提高反演结果的横向精度。实际资料的测试效果,也较好地展示了概率法反演技术的优点。
 |
| 图9 约束稀疏脉冲反演与概率法反演波阻抗效果对比 Fig. 9 Comparison between CSSI and probability inversion |
 |
| 图10 井间插值与地震约束确定横向趋势效果对比 Fig. 10 Comparison between well interpolation forward and seismic constraint forward |
图 11 为过A 井的约束稀疏脉冲反演剖面(图 11a)和概率法反演剖面(图 11b)。整体上看,概率法反演相对于约束稀疏脉冲反演,反演结果与井曲线匹配好。标注区域1,井上为两期砂体的纵向叠置关系,约束稀疏脉冲反演剖面上似乎有砂体叠置的影子,而从概率法反演结果上,两期砂体的叠置关系清晰,横向展布特征好。标注区域2,井上显示为两期砂体的纵向叠置关系,约束稀疏脉冲反演虽有两期砂体叠置的影子,但响应较弱,横向展布特征不好,而概率法反演结果很好地展现了砂体的叠置关系,砂体横向上有较好的展布特征。标注区域3,井上同样为两期砂体的叠置关系,约束稀疏脉冲反演剖面由于分辨率的缘故,显示为一期砂体,且有较好的横向展布特征,而概率法反演结果与井一致,显示为两套砂体垂向叠置,横向展布特征好。两者的对比说明,概率法反演具有较高的垂向分辨率和横向展布特征,能够满足油藏和地质对分辨率的需求。
 |
| 图11 约束稀疏脉冲反演与概率法反演效果对比 Fig. 11 Comparison between CSSI and probability inversion |
目标油田主要目的层段是明化镇组下段,曲流河沉积。目前钻井12 口。处于开发方案编制阶段。从平面属性及目前已钻遇的井间油水关系看,该地区砂体叠置连片,井间油水关系复杂(图 12),井间砂体的对比模式多解性强。这种砂体边界、叠置关系及油水关系的认识不清,直接影响油田开发井网部署和井位优化。
 |
| 图12 目标油田目的层段均方根振幅图 Fig. 12 RMS amplitude of target oilfield |
由上述探讨可知,概率法反演其独特的优势,可有效解决目标油田面临的上述地质难题,从而为井网部署和井位优化提供技术支持。
如图 13 所示,Well-1、Well-2 两口井相距仅2 km,井间油水关系矛盾,基于约束稀疏脉冲反演的结果,很难确定井间砂体的叠置关系是尖灭还是侧向叠置。解决该类问题的关键就是提高反演结果的垂向分辨能力。
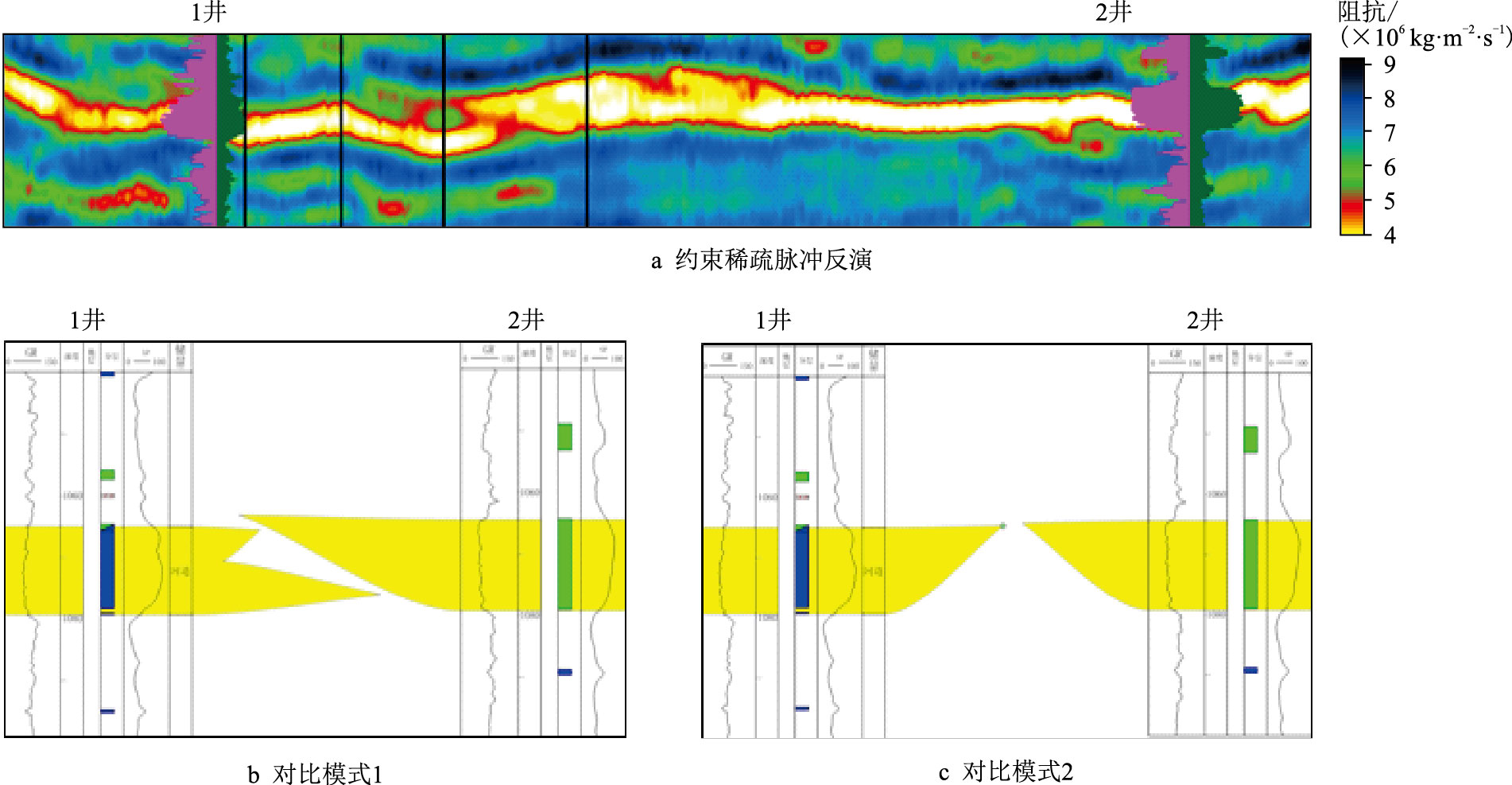 |
| 图13 井间砂体对比模式 Fig. 13 Comparing the mode between well 1 and well 2 |
图 14 为Well-1-1064 砂体与Well-2-1064 砂体原始砂体描述结果和新砂体描述结果对比,图 14a 为过Well-1、Well-2 井的约束稀疏脉冲反演剖面。两井钻遇的1064 砂体油水关系不统一,而反演剖面不能识别砂体横向不连通边界。从过Well-1、Well-2 的砂岩概率体剖面(图 14b)上可以清晰地刻画出Well-1-1064 砂体与Well-2-1064 砂体之间的叠置关系。基于砂岩概率体的新认识对1064 砂体重新解释,把1064 砂体分成两个在空间上相互叠置的砂体。
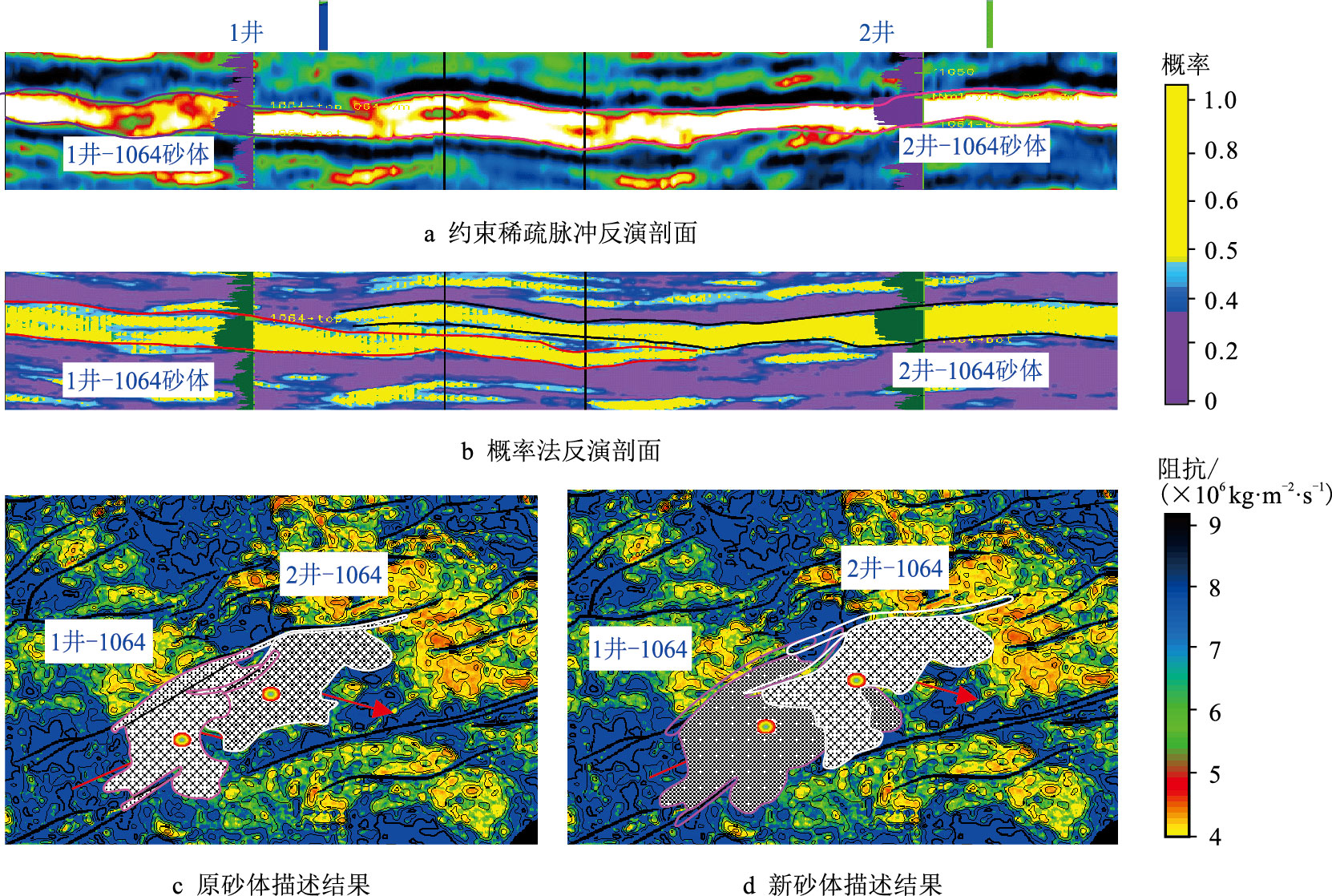 |
| 图14 1064 砂体原砂体描述结果与新砂体描述结果 Fig. 14 Original and new description of sand body well 1 1064 and well 2 1064 |
新砂体描述(图 14d)的砂体更符合对该地区的地质认识,相对于原始砂体描述结果(图 14c),在储量单元上发生了变化。
基于新的砂体描述认识,对Well-1-1064 砂体和Well-2-1064 砂体的井网部署进行了优化(图 15),图 15a 为原1064 砂体砂体描述结果与含油面积图,Well-1-1064 砂体主要为水层,有部分预测储量,Well-2-1064 砂体有探明、预测、控制3 部分储量。图 15c 中,原Well-2-1064 砂体井网部署B5h 井为水平生产井,水平段井轨迹位于图中所示位置。图 14d 中新砂体描述结果认为Well-2-1064砂体位于上部,原轨迹所打砂体为Well-2-1064 砂体。故将B5h 井改为定向井开发,落实新砂描的Well-2-1064 砂体是否为油,Well-1-1064 砂体是否为水。若落实Well-2-1064 砂体为油,再采用水平井开发。同时建议将B5h 井的轨迹微调为图 15b所示的红色虚线轨迹,来兼探Well-1-1064 砂体,落实该砂体井上0.9 m 厚储层的控制储量。
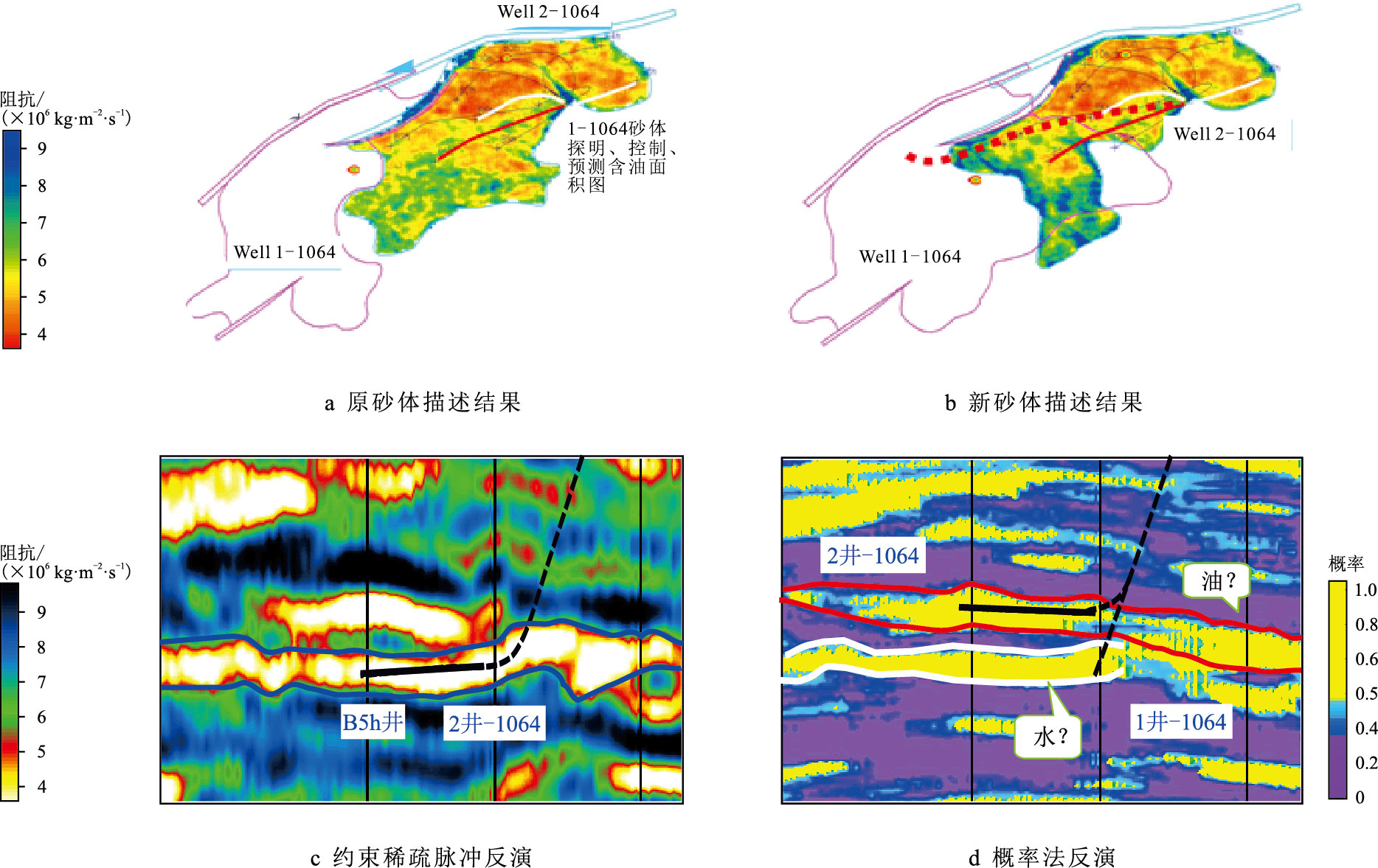 |
| 图15 1064 砂体井位优化图 Fig. 15 Well pattern deployment and well location optimization of sand body 1064 |
概率法反演技术有效地解决了砂体边界识别、砂体叠置关系分析及油水关系再认识问题,为井网部署和井位优化提供了有力依据。虽然概率法反演技术的应用前景乐观、思路也初步形成,不确定性的储层研究也逐步实现,但仍需不断实践、完善和深化。
| [1] |
胡华锋, 印兴耀, 吴国忱, 等. 基于贝叶斯分类的储层物性参数联合反演方法[J].
石油物探, 2012, 51 (3) : 225 –232.
HU Huafeng, YIN Xingyao, WU Guochen, et al. Joint inversion of petrophysical parameters based on Bayesian classification[J]. Geophysical Prospecting for Petroleum, 2012, 51 (3) : 225 –232. |
| [2] |
史祥明, 杨少春, 叶光辉, 等. 储集层平面非均质性的地质统计学研究方法[J].
新疆石油地质, 2010, 31 (5) : 497 –499.
SHI Xiangming, YANG Shaochun, YE Guanghui, et al. Geological statistics for study of reservoir areal heterogeneity[J]. Xinjiang Petroleum Geology, 2010, 31 (5) : 497 –499. |
| [3] |
周金应, 桂碧雯, 林闻. 多点地质统计学在滨海相储层建模中的应用[J].
西南石油大学学报(自然科学版), 2010, 32 (6) : 70 –73.
ZHOU Jinying, GUI Biwen, LIN Wen. Application of multiple-point geostatistics in offshore reservoir modeling[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2010, 32 (6) : 70 –73. |
| [4] |
尹艳树, 吴胜和, 翟瑞, 等. 利用Simpat模拟河流相储层分布[J].
西南石油大学学报(自然科学版), 2008, 30 (2) : 19 –22.
YIN Yanshu, WU Shenghe, ZHAI Rui, et al. The forecasting of fluvial facies reservoir distribution by using simpat[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2008, 30 (2) : 19 –22. |
| [5] |
尹艳树, 王进, 文志刚, 等. 浅水三角洲分流河道三维储层建模方法比较[J].
西南石油大学学报(自然科学版), 2013, 35 (3) : 46 –51.
YIN Yanshu, WANG Jin, WEN Zhigang, et al. Comparison of reservoir stochastic modeling methods for the underwater distributary channels in shallow water delta[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2013, 35 (3) : 46 –51. |
| [6] |
李文洁, 李辉峰, 张超, 等. 苏里格气田致密储集层定量描述技术[J].
新疆石油地质, 2014, 35 (4) : 476 –480.
LI Wenjie, LI Huifeng, ZHANG Chao, et al. Application of quantitative characterization technology for tight reservoirs in Sulige Gas Field[J]. Xinjiang Petroleum Geology, 2014, 35 (4) : 476 –480. |
| [7] |
王亚青, 高博禹, 孙立春. 提高地质储量计算精度需注意的几个问题[J].
西南石油大学学报(自然科学版), 2011, 33 (5) : 63 –67.
WANG Yaqing, GAO Boyu, SUN Lichun. Some problems in improving calculation precision OOIP[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2011, 33 (5) : 63 –67. |
| [8] | DUBRULE O, THIBAUT M, LAMY P, et al. Geostatistical reservoir characterization constrained by 3D seismic data[J]. Petroleum Science, 1998 (4) : 121 –128. |
| [9] |
姜文龙, 杨锴. 岩石物理参数高分辨率地质统计学反演[J].
石油物探, 2012, 51 (6) : 638 –649.
JIANG Wenlong, YANG Kai. High-resolution geostatistical petrophysical-parameter inversion[J]. Geophysical Prospecting for Petroleum, 2012, 51 (6) : 638 –649. |
| [10] | HAAS A, DUBRULE O. Geostatistical inversion-A sequential method for stochastic reservoir modeling constrained by seismic data[J]. First Break, 1994, 13 (12) : 561 . |
| [11] | ROTHMAN D H. Geostatistical inversion of 3-D seismic data for thin-sand delineation[J]. Geophysics, 1998, 51 (2) : 332 –346. |
| [12] |
王香文, 刘红, 滕彬彬, 等. 地质统计学反演技术在薄储层预测中的应用[J].
石油与天然气地质, 2012, 33 (5) : 730 –735.
WANG Xiangwen, LIU Hong, TENG Binbin, et al. Application of geostatistical inversion to thin reservoir prediction[J]. Oil & Gas Geology, 2012, 33 (5) : 730 –735. |
| [13] |
何火华, 李少华, 杜家元, 等. 利用地质统计学反演进行薄砂体储层预测[J].
物探与化探, 2011, 35 (6) : 804 –808.
HE Huohua, LI Shaohua, DU Jiayuan, et al. The application of geostatistic inversion method to predicting the thin sandstone reservoir[J]. Geophysical & Geochemical Exploration, 2011, 35 (6) : 804 –808. |
| [14] |
吕其彪, 吴清杰, 毕有益. 高分辨率地质解释预测礁滩相储集层[J].
新疆石油地质, 2012, 33 (5) : 557 –559.
LV Qibiao, WU Qingjie, BI Youyi. Prediction of reep-flat revervoir using high resolution seismic interpretation[J]. Xinjiang Petroleum Geology, 2012, 33 (5) : 557 –559. |
| [15] |
尚建林, 李太辉, 霍新勇, 等. 地质统计学反演预测百口泉油田百34井区薄砂体[J].
新疆石油地质, 2009, 30 (6) : 758 –760.
SHANG Jianlin, LI Taihui, HUO Xinyong, et al. Applicaton of geostatistical inversion to prediction of thin sand body of Karamay Formation in Bai-34 well area in Baikouquan Oil Field[J]. Xinjiang Petroleum Geology, 2009, 30 (6) : 758 –760. |
| [16] |
宋维琪, 朱海伟, 姜宇东, 等. 地面微地震资料震源定位的贝叶斯反演方法[J].
石油物探, 2013, 52 (1) : 11 –16.
SONG Weiqi, ZHU Haiwei, JIANG Yudong, et al. Bayesian inversion method for surface monitoring microseismic data[J]. Geophysical Prospecting for Petroleum, 2013, 52 (1) : 11 –16. |
| [17] |
宗兆云, 印兴耀, 张繁昌. 基于弹性阻抗贝叶斯反演的拉梅参数提取方法研究[J].
石油地球物理勘探, 2011, 46 (4) : 598 –604.
ZONG Zhaoyun, YIN Xingyao, ZHANG Fanchang. Elastic impedance Bayesian inversion for Lame paramaters extracting[J]. Oil Geophysical Prospecting, 2011, 46 (4) : 598 –604. |
| [18] | PENDREL J, LEGGETT M, MESDAG P. Geostatistical simulation for reservoir characterization[J]. CSEG Annual M fleeting Abstracts, 2004 . |
| [19] | TORRES-VERDN C, GRIJALBA-CUENCA A, DEBEYE H W J. A Comparison between geostatistical inversion and conventional geostatistical-simulation practices for reservoir delineation[C]. AAPG Hedberg Research Conference on Applied Reservoir Characterization Using Geostatistics, 2005, 316. |
| [20] |
张义, 尹艳树, 秦志勇. 地质统计学反演在薄砂体储层预测中的应用[J].
断块油气田, 2015, 22 (5) : 565 –569.
ZHANG Yi, YIN Yanshu, QIN Zhiyong. Application of geostatistical inversion in thin sandstone reservoir prediction[J]. Fault-Block Oil & Gas Field, 2015, 22 (5) : 565 –569. |
| [21] |
肖佃师, 卢双舫, 王海生, 等. 三角洲外前缘薄砂体地震综合预测方法[J].
中国石油大学学报(自然科学版), 2015, 39 (4) : 62 –69.
XIAO Dianshi, LU Shuangfang, WANG Haisheng, et al. Comprehensive prediction method of seismic to thin sandstone reservoir in delta-frontal[J]. Journal of China University of Petroleum(Edition of Natural Science), 2015, 39 (4) : 62 –69. |
| [22] |
张飞飞, 王珩, 郭永贵, 等. 密井网地质统计学反演在河道砂体预测中的应用[J].
断块油气田, 2016, 23 (2) : 156 –160.
ZHANG Feifei, WANG Heng, GUO Yonggui, et al. Application of dense well geological statistics inversion in prediction of channel sand body[J]. Fault Block Oil & Gas Field, 2016, 23 (2) : 156 –160. |
| [23] |
韩东, 胡向阳, 乌兴威, 等. 基于马蒙算法地质统计学反演的缝洞储集体预测[J].
物探与化探, 2015, 39 (6) : 1211 –1216.
HAN Dong, HU Xiangyang, WU Xingwei, et al. The prediction research on fracture-cavity reservoirs by geostatistical inversion based on Markov Chain and Monte-Carlo algorithm in the Tahe Oilfield[J]. Geophysical and Geochemical Exploration, 2015, 39 (6) : 1211 –1216. |
 2016, Vol. 38
2016, Vol. 38


