2. 成都九鼎科技(集团)有限公司, 四川 成都 610100;
3. 中国石油技术开发公司, 北京 西城 100009;
4. 中国石油长庆油田公司油田开发处, 陕西 西安 751500
2. Chengdu Jiuding Technology(group) Co. Ltd., Chengdu, Sichuan 610100, China;
3. China Petroleum Technology and Development Corporation, Xicheng, Beijing 100009, China;
4. Department of Oilfield Development, Changqing Oilfield Company, PetroChina, Xi'an, Shaanxi 751500, China
螺杆机械螺旋面铣削加工原理主要有成形铣和包络铣。前者不仅加工效率低,而且对于不同尺寸、型号的螺杆要配备不同的刀具以及使用过程中磨损导致的误差等因素,仅适用于单件生产及精度要求不高的场合;后者将包络铣削技术与数控技术结合,采用盘铣刀包络铣削螺杆,比成形铣削效率高、柔性好、成本低,是目前加工复杂螺旋曲面采用最多的方法之一[1-5]。包络铣削包括截面包络铣削和空间包络铣削两种刀位轨迹插补原理,截面包络铣削是将刀具与工件的空间啮合关系简化为工件截面内的平面问题,这会导致工件加工过程中出现干涉现象,只适合于刀尖圆弧半径小、加工小螺旋角螺杆的情况;空间包络铣削的刀位轨迹按照工件与刀具的实际空间啮合情况进行计算,可以判断干涉情况,并加以消除,加工精度高,从20 世纪90 年代中期以后已经发展成为国际上主要的包络铣削理论[6-8]。
计算刀位轨迹数控代码的数学模型及算法是空间包络铣削的关键,其主要原理为:以工件螺旋面及刀具圆环面方程为基础,基于切削点法向量重合的原理建立刀具-工件啮合轨迹模型;以啮合点及工件与刀具的相互几何关系为基础,建立包含刀具中心坐标的非线性微分方程组,从而得到刀位轨迹数学模型;最后通过数值方法的求解以及误差控制的插补算法最后得到数控代码[1]。该方法数学理论较为复杂,编程实现有一定难度,对于非连续螺旋面截形方程在求解过程中需要做特殊处理。本文基于计算机仿真的思想,提出了一种数学原理简单、易于编程实现的刀位轨迹计算方法,通过对加工过程进行时间离散化,以及工件和刀具的三维模型进行空间离散化来求解刀位轨迹,而无需进行曲线拟合和复杂的数值求解。基于该方法生成的数控代码加工精度高,同时也能适用于多种复杂螺旋面的空间包络铣刀位轨迹的计算。
1 基本原理假设已知螺旋面截形点坐标及圆盘铣刀基本尺寸参数,采用时间离散化和空间离散化的数值仿真思想,将连续的切削行为离散化成离散的时间点上两个空间曲面的啮合关系,并通过算法直接求解各时刻所对应的刀位点,而不需要推导描述啮合轨迹及刀位轨迹方程。
(1)时间离散化:将刀具对螺旋面进行空间包络的连续切削过程离散化为多个时刻发生的啮合行为的集合,依序求解出在每个时刻上刀具的刀位点集。
(2)空间离散化:在同一坐标系内,用垂直于刀具中心轴的等间距平面将刀具和工件的空间曲面离散化为一一对应的空间曲线对。沿进刀方向,各对应曲线对间均存在一个最小距离,所有对应曲线对间最小距离的最小值即为两曲面间的最小有向距离,其对应的点即为刀具沿进刀方向进给时与目标螺旋面的啮合点。
由此,可以反推得到刀具的刀位轨迹点集,并依据确定的插补原理,可以按照数值迭代算法得到规定误差限范围内的刀位轨迹插补点集,并最终得到数控加工代码。通过求解最小有向距离来得到刀位轨迹是数值算法的核心,并且已经有一些研究成果[9-11],本文提出了一种简单的非迭代寻优算法。
2 刀位轨迹数值仿真方法 2.1 目标螺旋面及刀具三维模型 2.1.1 螺旋面三维模型的建立设螺旋面坐标系为$oxyz$,端面截形为
| ${\textbf{r}} = x_0 (u){\textbf{i}} + y_0 (u){\textbf{j}}$ | (1) |
式中:r 端面截形的矢径;
u 端面截形参变数;
${\textbf{i}},{\textbf{j}} $ 坐标系$oxyz$ 中$x,y$ 方向的单位向量。
在坐标系$oxyz$ 中,端面截形绕z 轴旋转的同时又沿z 轴正方向移动,即为螺旋运动,得到空间螺旋曲面[12-14]。设端面廓形沿z 轴正方向作导程为L的螺旋运动(以左旋为例),得到在$oxyz$ 坐标系下一个导程内的空间螺旋曲面,其表达式为
| $\left\{ \begin{array}{l} x = x_0 (u)\cos \theta + y_0 (u)\sin \theta \\ y = - x_0 (u)\sin \theta + y_0 (u)\cos \theta \\ z = p\theta \\ \end{array} \right.$ | (2) |
式中:x,y,z 空间螺旋曲面在x 轴、y 轴、z 轴上的坐标分量值,mm;
θ 螺旋角度参变量,rad;
p 螺旋参数,mm/rad。
基于上述模型在数值计算软件中生成的螺旋面三维模型如图 1 所示(模型轴向为z 轴,端面为xoy坐标平面)。
 |
| 图1 螺旋面三维模型 Fig. 1 The 3D model of helical surface |
在包络铣中,所用的刀具为圆盘铣刀。这种刀具是在盘铣刀体上,安装刀尖半径为r 的标准机夹刀片,设盘铣刀半径为$R_0$,盘铣刀截面示意图如图 2a 所示。在切削加工过程中,刀盘作主切削运动,以高速度旋转形成回转面,参与切削工件的刀尖圆弧部分绕其自身轴线旋转形成回转面,其截面如图 2b 所示[1, 15]。
 |
| 图2 盘铣刀截面示意图 Fig. 2 Sketch map of disc-type milling cutter and cutting corner arc cross section |
建立刀具坐标系$OXYZ$,圆环截面廓形(圆母线)的极坐标数学模型按式(3)建立,将其旋转360°得到刀具三维模型,如图 3 所示(模型竖直方向为Z轴方向,水平面为$XOY$ 坐标平面),再通过坐标变换转换成直角坐标。
| $(R - R_0 )^2 + Z^2 = r^2$ | (3) |
式中:R 圆环截面廓形上各点的极径,mm;
Z 圆环截面廓形上各点的高度坐标值,mm;
r 刀尖半径,mm。
 |
| 图3 刀具三维模型 Fig. 3 The 3D model of cutting tool |
数值仿真计算时,需要将工件与刀具曲面用离散点坐标表示,其各点的坐标可表示成如下矩阵
工件坐标矩阵
| $[x,y,z] = \left[ {\begin{array}{*{20}c} {x_1 } & {y_1 } & {z_1 } \\ {x_2 } & {y_2 } & {z_2 } \\ {...} & {...} & {...} \\ {x_n } & {y_n } & {z_n } \\ \end{array}} \right]$ | (4) |
刀具坐标矩阵
| $[X,Y,Z] = \left[ {\begin{array}{*{20}c} {X_1 } & {Y_1 } & {Z_1 } \\ {X_2 } & {Y_2 } & {Z_2 } \\ {...} & {...} & {...} \\ {X_n } & {Y_n } & {Z_n } \\ \end{array}} \right]$ | (5) |
对于每一个离散时间间隔,将刀具与工件同时进行的运动分解为两者的先后运动,即工件先绕$oxyz$坐标系z 轴转动后,刀具再沿$OXYZ$坐标系X方向向工件移动,工件绕z轴转动,其坐标转换可由旋转变换矩阵式(6)实现。
| ${\textbf{T}}_1 = \left[ {\begin{array}{*{20}c} {\cos t_3 } & { - \sin t_3 } & 0 & 0 \\ {\sin t_3 } & {\cos t_3 } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}} \right]$ | (6) |
式中:$t_3$-工件相对于起始位置绕z轴旋转的角度,rad。
数值计算时必须统一坐标系,本文为了计算方便,以刀具的坐标系为主坐标系,在工件绕z 轴转动后,运用式(7)和式(8)将工件曲面离散点转换到刀具坐标系中,如图 4 所示。其中,式(7)为沿x 轴的平移矩阵,式(8)为绕x 轴旋转变换矩阵[16-18]。
| ${\textbf{T}}_2 = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ a & 0 & 0 & 1 \\ \end{array}} \right]$ | (7) |
| ${\textbf{T}}_3 = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {\cos B} & {\sin B} & 0 \\ 0 & { - \sin B} & {\cos B} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}} \right]$ | (8) |
式中:a 在x 轴方向的平移量,mm;
B 工件绕x 轴旋转角度,其值为工件中径螺旋角的余角,rad。
 |
| 图4 刀具与工件计算示意图 Fig. 4 The computing graphic of cutter and workpiece |
因此,工件的仿真模型[$x^{'}、y^{'}、z^{'}$]由式(9)可得,刀具的离散点坐标矩阵不变,仍为[X、Y、Z]。
| $[x',y',z',1] = \left[ {\begin{array}{*{20}c} {x_1 '} & {y_1 '} & {z_1 '} & 1 \\ {x_2 '} & {y_2 '} & {z_2 '} & 1 \\ {...} & {...} & {...} & 1 \\ {x_n '} & {y_n '} & {z_n '} & 1 \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {x_1 } & {y_1 } & {z_1 } & 1 \\ {x_2 } & {y_2 } & {z_2 } & 1 \\ {...} & {...} & {...} & 1 \\ {x_n } & {y_n } & {z_n } & 1 \\ \end{array}} \right]{\textbf{T}}_1 {\textbf{T}}_2 {\textbf{T}}_3$ | (9) |
刀具曲面与工件螺旋面间最小有向距离的求解算法是本研究的核心,本文采用一种创新的三维模型空间离散化方法进行数值求解。最小有向距离原理已在文献[9-11] 中阐述,这里就不作介绍。
如图 4 所示,假设刀具模型的轴向高度为$2h$,采用从$-h$到h垂直于Z轴的一系列等间距平面将刀具与工件曲面离散化,各垂直面的Z坐标值记为$Z_{\rm{h}}$,在各平面上刀具与工件的廓形为两条曲线点集。设一共有p个等间距平面,第k(k=1,2,3,…,p)个平面上刀具曲线点集记为$F_k (X,Y)$,工件曲线点集记为$f_k (x',y')$,用工件曲线点集$f_k (x',y')$ 各点间在Y 轴上的步长统一刀具曲线点集$F_k (X,Y)$各点间在Y 轴上的步长,如图 5 所示,则该平面上两曲线的X 方向的最小距离$L_k$ 为
| $L_k = \min \left[ {F_k (X,Y) - f_k (x^{'} ,y^{'} )} \right] = \\\min \left[ {(X_{1{'}} - x_1{'}),(X_{2{'}} - x_2{'}),(X_{3{'}} - x_3{'}),...,(X{}_{j{'}} - x_j{'})} \right]$ | (10) |
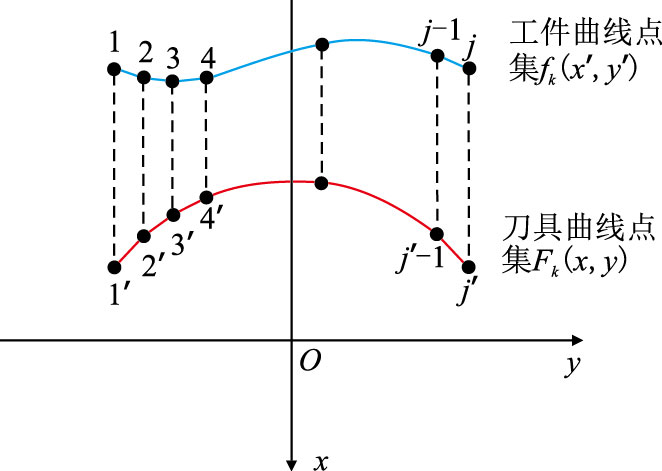 |
| 图5 平面上刀具与工件曲线点集 Fig. 5 Point sets on the curve of cutter and workpiece |
两曲面在X 方向上的最小距离D 为
| $D = \min (L_1 ,L_2 ,L_3 ,...,L_p )$ | (11) |
D 所对应的曲面上的点即为两曲面的啮合点。两曲面在X 方向的最小距离求解过程如图 6 所示。
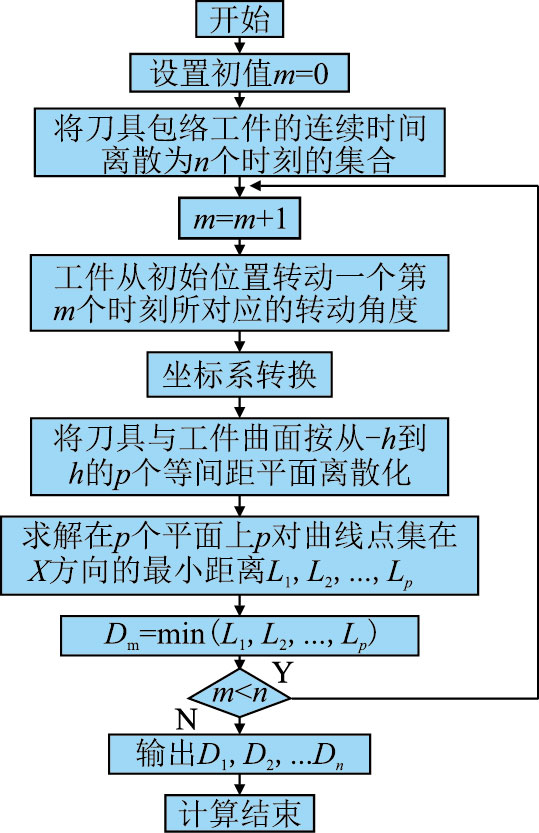 |
| 图6 求解流程图 Fig. 6 Flow chart of solution algorithm |
实际加工中,刀具与工件的相对位置如图 7 所示,刀具的坐标系为$OXYZ$,工件的坐标系为$oxyz$,刀具相对工件安装角为e,此角度为螺旋曲面中径处的螺旋角。加工过程中,工件绕z轴旋转,刀具沿X轴进给,刀具坐标系的X轴与工件坐标系的x轴同向。在刀具包络工件一周的加工过程中,刀具的刀位点只在X轴方向变化,设在任意先后相邻两个时刻上刀位点在X轴上的坐标值为$X_i$、$X_{i+1}$,坐标值变化量为d,则
| $X_{i + 1} = d + X_i$ | (12) |
所以,要求解刀位轨迹可以先通过求解在各个时刻刀位点的X坐标变化值d,再利用递推的方法得到各个时刻上的刀位点。
 |
| 图7 刀具与工件的相对位置图 Fig. 7 Position relationship between the cutter and workpiece |
如2.2所述,将刀具与工件的2轴联动分解为工件绕z轴转动与刀具沿X方向向工件移动两个顺序运动,直到刀具与加工工件目标螺旋曲面接触为止,接触点就为啮合点,刀具在X方向的移动距离就为刀具曲面与工件曲面在X方向的最小有向距离,最小距离为D。在每一个离散时刻,假设刀位点初始位置不变,即刀位点初始坐标值已知,记为($X_1$,$Y_1$,$Z_1$)。设在任意先后相邻两个时刻上刀具曲面与工件曲面在X方向的最小有向距离为$D_i$、$D_{i+1}$,则刀位点坐标值变化量d为
| $d = - (D_{i + 1} - D_i )$ | (13) |
综上所述,第i+1(i=1、2、…、$n-1$)个时刻刀位轨迹点坐标为
| $\left\{ \begin{array}{l} X_{i + 1} = - (D_{i + 1} - D_i ) + X_i \\ Y_{i + 1} = Y_1 \\ Z_{i + 1} = Z_1 \\ \end{array} \right.$ | (14) |
以刀具包络工件的中截面廓形误差来控制各插补点间的插补步长。在工件中截面上,根据上面计算出的刀位轨迹,将刀具在工件中截面上的截面廓形绕工件z 轴逆时针方向按照阿基米德螺旋线生成原理运动,如图 8 所示。通过在每一个时刻刀具截面廓形与工件截面廓形的最小法向距离与误差控制值的比较,插补迭代计算出编制数控程序的插补点集(X、C),最后自动生成数控加工程序[19-20]。
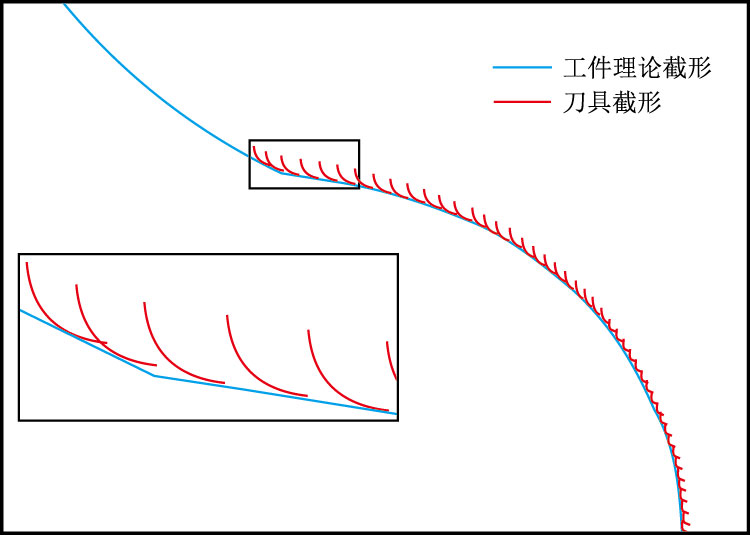 |
| 图8 中截面上包络过程图 Fig. 8 The envelope process in the middle cross section |
基于上述理论,开发了螺杆加工的仿真程序,并对某型螺杆钻具芯轴的数控加工代码进行了计算。该钻具理论截形数据为
极角极径
0 104.253 0
0 0 104.247 0
1.000 0 104.209 4
……
其他参数包括:导程1 000 mm,左旋。刀具参数为:刀盘半径140 mm,刀尖角350,刀尖圆弧半径1.2 mm。程序插补精度(误差控制值)为0.05 mm。采用本文的仿真算法生成的数控代码为
N100 X-0.013 C 0.600 F 1800
N110 X-0.080 C 0.900 F 1776
N120 X-0.131 C 0.800 F 1752
……
仿真得到的截面误差与截形对比见图 9、图 10。图 9 中的误差基本上都控制在0.05 mm 内,只有少部分的误差超出了误差控制值,原因有两个方面:(1)由于刀具是空间包络工件,形成空间啮合轨迹,在截面上存在理论误差;(2)由于理论廓形存在不同曲线廓形的交点,该点处二阶导不连续,即在截面上存在尖点,该点附近与刀具插补曲线存在较大误差,如图 9 中在极角22° 左右处的误差值。
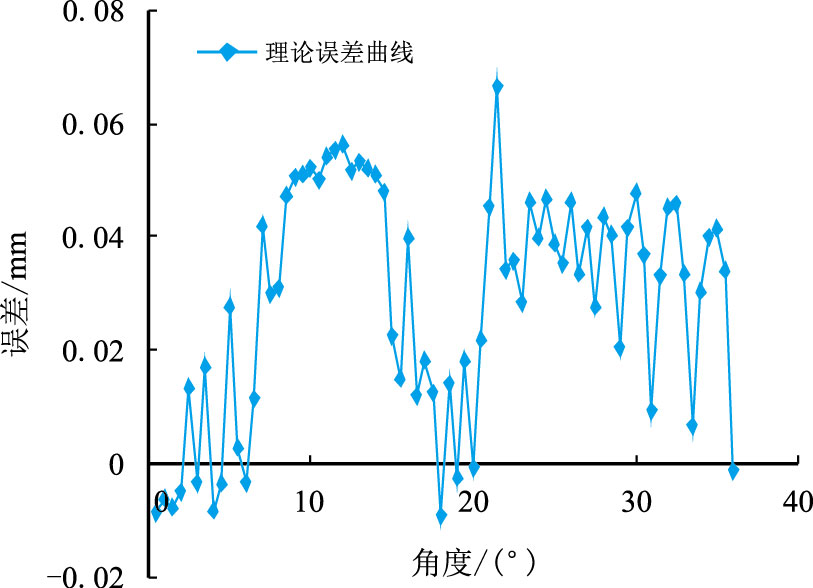 |
| 图9 仿真截形误差分布图 Fig. 9 Error distribution of the simulated curve |
 |
| 图10 仿真截形与理论截形对比图 Fig. 10 Comparison between the simulated and theoretical curve |
用生成的数控程序加工出的螺杆样品如图 11 所示,其截形误差分布如图 12,图 13 所示。为得到准确合理的加工截面分析数据,运用三坐标仪测量图 11 中螺杆的多个截面,以平均值作为误差分析数据。图 12 中的螺杆截面误差是理论误差、加工误差、测量误差3 个方面的综合。经实验测试,其工作性能良好,能很好地满足对螺杆钻具工作效率的要求。
 |
| 图11 螺杆实物 Fig. 11 The actual screw |
 |
| 图12 加工截面误差分布图 Fig. 12 Comparison between the processed and theoretical curve |
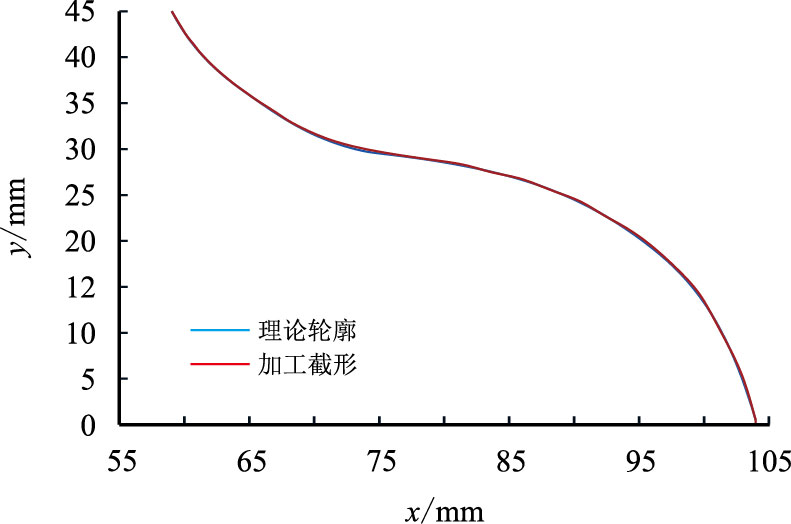 |
| 图13 加工截形与理论截形对比图 Fig. 13 Comparison between the processed and theoretical curve |
(1)提出的数值仿真算法对于复杂螺旋曲面的数控加工刀位轨迹的求解是一种原理简单、高效精确的有效算法。
(2) 运用数值仿真的思想,将时间、空间离散化,以及运动分解,使仿真计算程序简单易实现,容易得到复杂螺旋曲面的数控加工自动编程系统。
(3)该方法对截形方程没有特殊要求,对于一阶导数连续曲线或多段曲线组成的截形均可在廓形点确定的情况下进行数值仿真得到刀位轨迹,并且还可以根据本文的方法和原理,通过编程实现对刀具安装角、刀尖圆角半径、刀尖角等参数的灵活选择。
| [1] |
WANG Ke. Research for milling with non-instantaneouspole envelope theory applying technology of complex and abnormal helical surface[D]. Tianjin:Tianjin University, 2003.
王可. 复杂异形螺旋曲面无瞬心包络铣削理论及应用技术研究[D]. 天津:天津大学, 2003. |
| [2] |
PEI Liqun. Research of programming error analysis algorithm for machining complex surface[D]. Shenyang:Shenyang University of Technology, 2005.
裴立群. 复杂曲面数控加工中编程误差分析方法研究[D]. 沈阳:沈阳工业大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10142-2005083292.htm |
| [3] |
HE Xiaomei. Programming error analysis method for machining spiral rod[D]. Shenyang:Shenyang University of Technology, 2002.
何小妹. 螺杆加工中编程误差分析方法研究[D]. 沈阳:沈阳工业大学, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10142-2003124224.htm |
| [4] |
XU Yinlong. Research on 3D dynamic simulation technology for special helical pole machining process[D]. Shenyang:Shenyang University of Technology, 2006.
许银龙. 异形螺杆加工过程三维动态仿真技术研究[D]. 沈阳:沈阳工业大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10142-2006100212.htm |
| [5] |
LI Hui. Research of on-line measurement technology for spiral curved surface end cross-section shape[D]. Shenyang:Shenyang University of Technology, 2005.
李卉. 螺旋曲面廓形的在线测量技术研究[D]. 沈阳:沈阳工业大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10142-2005083231.htm |
| [6] |
ZHAO Wei. Study on milling helical-surface machining technique with four-axial non-instaneous envelope[D]. Shenyang:Shenyang University of Technology, 2002.
赵巍. 四自由度无瞬心包络铣削螺旋曲面加工方法研究[D]. 沈阳:沈阳工业大学, 2002. |
| [7] |
王可, 赵文珍, 唐宗军, 等. 异形螺杆无瞬心包络铣削技术研究[J].
中国机械工程, 2001, 12 (3) : 294 –296.
WANG Ke, ZHAO Wenzhen, TANG Zongjun, et al. Machining technology research on non-instantaneous-pole envelope of special spiral rod[J]. China Mechanical Engineering, 2001, 12 (3) : 294 –296. |
| [8] |
柏占伟. 多自由度包络铣削异形螺杆接触迹分析[J].
机械, 2009, 36 (4) : 5 –8.
BAI Zhanwei. Analysis of the contact-track of multiaxis envelope milling abnormal spiral-rod[J]. Machinery, 2009, 36 (4) : 5 –8. |
| [9] |
赵文珍, 何小妹, 王维, 等. 最小有向距离算法在螺杆加工中的应用[J].
中国机械工程, 2002, 13 (5) : 371 –373.
ZHAO Wenzhen, HE Xiaomei, WANG Wei, et al. The algorithm of seeking mininmal orientation-distance in screw-rod machining process[J]. China Mechanical Engineering, 2002, 13 (5) : 371 –373. |
| [10] |
赵文珍, 张新建. 基于最小有向距离原理的无干涉刀位轨迹计算[J].
机械工程师, 2007 (10) : 7 –9.
ZHAO Wenzhen, ZHANG Xinjian. Interference free tool path algorithm based on the principle of minimal orientation-distance[J]. Mechanical Engineer, 2007 (10) : 7 –9. |
| [11] |
王中宝. 螺旋面数控加工刀具运动轨迹计算方法研究[J].
机械研究与应用, 2007, 20 (1) : 36 –37.
WANG Zhongbao. NC tool-path generation method for machining of helical surface[J]. Mechanical Research & Application, 2007, 20 (1) : 36 –37. |
| [12] |
汪国平, 华宣积, 孙家广. 复杂螺旋曲面铣削加工的几何特性分析[J].
清华大学学报(自然科学版), 2000, 40 (9) : 49 –52.
WANG Guoping, HUA Xuanji, SUN Jiaguang. Geometric characteristic analysis of the milling of Helicoids[J]. Journal of Tsinghua University(Sci & Tech), 2000, 40 (9) : 49 –52. |
| [13] |
苏义脑.
螺杆钻具研究及应用[M]. 北京: 石油工业出版社, 2001 .
SU Yinao. The study of PDM and application[M]. Beijing: Petroleum Industry Press, 2001 . |
| [14] | Litvin F L, Fuentes A. Gear Geometry and Applied Theory[J]. Mechanism & Machine Theory, 1994, 30 (3) : 493 –493. |
| [15] |
易先中, 何俊松, 华北庄. 复杂螺旋曲面成形铣削刀具的工艺参数研究[J].
石油机械, 1999, 27 (5) : 16 –19.
YI Xianzhong, HE Junsong, HUA Beizhuang. Research on technological parameters of forming milling technique in machining complex spiral curved surfaces[J]. China Petroleum Machinery, 1999, 27 (5) : 16 –19. |
| [16] |
况雨春, 杨高, 伍开松, 等. 基于MATLAB的三牙轮钻头仿真模型研究[J].
钻采工艺, 2006, 29 (6) : 83 –86.
KUANG Yuchun, YANG Gao, WU Kaisong, et al. Research on simulation model of tri-cone bits by using Matlab[J]. Drilling & Production Technology, 2006, 29 (6) : 83 –86. |
| [17] |
吴序堂.
齿轮啮合原理[M]. 北京: 机械工业出版社, 1982 .
WU Xutang. Theory of gearing[M]. Beijing: China Machine Press, 1982 . |
| [18] |
姚俊, 张玉春.
工程矩阵方法[M]. 北京: 国防工业出版社, 2007 .
YAO Jun, ZHANG Yuchun. Engineering matrix method[M]. Beijing: National Defence Industry Press, 2007 . |
| [19] |
杜国臣, 王士军.
机床数控技术[M]. 北京: 北京大学出版社, 2001 .
DU Guochen, Wang Shijun. NC machine tool technology[M]. Beijing: Peking University Press, 2001 . |
| [20] |
肖民, 何云.
数控机床加工工艺与操作技术[M]. 上海: 华东理工大学出版社, 2012 .
XIAO Min, HE Yun. Processing technology and operation technology of NC machine tools[M]. Shanghai: East China University of Science and Technology Press, 2012 . |
 2016, Vol. 38
2016, Vol. 38


