在均质地层中,由于地层本身或者在钻井过程中钻井液的侵入等原因,导致近井地带和远井地带形成两种不同地层或流体参数的渗流区,即为复合油藏。目前,关于复合油藏试井分析模型求解方面的研究成果很多[1-3],多数文章仅给出了模型的半解析解。有些文章运用Stehfest 数值反演法,对模型进行了数值求解,但是由于对虚宗量Bessel 函数的数值计算处理不当,导致计算精度不够,结果有曲线震荡问题的出现,对后续的试井分析中的曲线拟合造成了很大的困扰。对此,采用Stehfest 数值反演法获得实空间解,引入有效的虚宗量Bessel 函数的分段数值算法,提高了数值计算精度,不仅绘制的曲线平滑完整,而且增快了计算速度,对此后试井分析软件的编制和现场的运用具有较大的参考意义。
1 复合油藏数学模型考虑具有井筒储集和表皮效应影响的复合油藏,由两个同心区域(内区+ 外区)组成,复合油藏试井模型考虑以下基本条件:
(1)单相微可压缩流体在储层中的平面径向渗流。
(2)流体流动为等温过程且服从达西定律。
(3)地层等厚,地层中存在两种不同物性参数渗流区,两个渗流区界面不存在附加压力降。
在考虑了井筒储集系数和表皮因子以后,对复合油藏的无因次数学模型方程和定解条件为[4-5]:
渗流方程
| $\left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{\rm{d}}^2} {{p_{1{\rm{D}}}}} }}{{{\rm{d}}{r_{\rm{D}}}^2}} + \dfrac{1}{{{r_{\rm{D}}}}}\dfrac{{{\rm{d}} {{p_{1{\rm{D}}}}} }}{{{\rm{d}}{r_{\rm{D}}}}} = z {{p_{1{\rm{D}}}}} {\kern 20pt}{\rm{ (1}} \leqslant {r_{\rm{D}}} \leqslant {\rm{\alpha )}}}\\[9pt] {\dfrac{{{{\rm{d}}^2} {{p_{2{\rm{D}}}}} }}{{{\rm{d}}{r_{\rm{D}}}^2}} + \dfrac{1}{{{r_{\rm{D}}}}}\dfrac{{{\rm{d}} {{p_{2{\rm{D}}}}} }}{{{\rm{d}}{r_{\rm{D}}}}} = {\rm{\sigma }}z {{p_{2{\rm{D}}}}} {\kern 14pt} {\rm{(\alpha }} \leqslant {r_{\rm{D}}}{\rm{)}}} \end{array}} \right.$ | (1) |
内边界条件
| $\left\{ {\begin{array}{*{20}{l}} { {{p_{{\rm{WD}}}}} (z) = {{\left( { {{p_{1{\rm{D}}}}} - S{r_{\rm{D}}}\dfrac{{tial {{p_{1{\rm{D}}}}} }}{{tial {r_{\rm{D}}}}}} \right)}_{{r_{\rm{D}}} = 1}}}\\[9pt] {{{\left( {{r_{\rm{D}}}\dfrac{{tial {{p_{1{\rm{D}}}}} }}{{tial {r_{\rm{D}}}}}} \right)}_{{r_{\rm{D}}} = 1}} = - {{q_{\rm{D}}}} {\rm{(}}z{\rm{) + }}{C_{\rm{D}}}z {{p_{{\rm{WD}}}}} } \end{array}} \right.$ | (2) |
衔接条件
| $\left\{ {\begin{array}{*{20}{l}} { {{p_{1{\rm{D}}}}} ({\rm{\alpha }},z) = {{p_{2{\rm{D}}}}} ({\rm{\alpha }},z)}\\[9pt] {\dfrac{{tial {{p_{1{\rm{D}}}}} }}{{tial {r_{\rm{D}}}}}{|_{{r_{\rm{D}}} = {\rm{\alpha }}}} = \lambda \dfrac{{tial {{p_{2{\rm{D}}}}} }}{{tial {r_{\rm{D}}}}}{|_{{r_{\rm{D}}} = {\rm{\alpha }}}}} \end{array}} \right.$ | (3) |
外边界条件
| $\left\{ {\begin{array}{*{20}{l}} { {{p_{2{\rm{D}}}}} \left( {{r_{\rm{D}}} \to \infty ,z} \right) = 0 {\kern 30pt}(无限大边界)}\\[6pt] { {{p_{2{\rm{D}}}}} \left( {{R_{\rm{D}}},z} \right) = 0 {\kern 53pt} (定压边界)}\\[6pt] {\dfrac{{tial {{p_{2{\rm{D}}}}} }}{{tial {r_{\rm{D}}}}}{|_{{r_{\rm{D}}} = {R_{\rm{D}}}}} = 0 {\kern 52pt} (封闭边界)} \end{array}} \right.$ | (4) |
其中:${p_{1{\mathop{\rm D}\nolimits} }} = \dfrac{{2\pi {K_1}h}}{{{q_{\rm{e}}}\mu B}}({p_{\rm i}} - {p_1})$;${p_{2{\mathop{\rm D}\nolimits} }} = \dfrac{{2\pi {K_2}h}}{{{q_{\rm{e}}}\mu B}}({p_{\rm i}} - {p_2})$;${r_{\mathop{\rm D}\nolimits} } = \dfrac{r}{{{r_{\mathop{\rm w}\nolimits} }}}$;$\sigma = \dfrac{{{K_1}{\phi _2}{\mu _2}{C_{\rm t2}}}}{{{K_2}{\phi _1}{\mu _1}{C_{\rm t1}}}}$;${p_{{\rm{}}{\mathop{\rm WD}\nolimits} }} = \dfrac{{2\pi {{\mathop{\rm K}\nolimits} _1}h}}{{{q_{\rm{e}}}\mu B}}\left( {{p_{\rm i}} - {p_{\rm{W}}}} \right)$;${q_{\mathop{\rm D}\nolimits} } = \dfrac{q}{{{q_{\mathop{\rm e}\nolimits} }}}$;${C_{\mathop{\rm D}\nolimits} } = \dfrac{C}{{2\pi {\phi _1}{C_{\rm t1}}h\mathop r\nolimits_{\mathop{\rm w}\nolimits} ^2 }}$;${R_{\rm D}} = \dfrac{R}{{{r_{\rm{w}}}}}$。
常微分方程式(1)、式(2)都是虚宗量贝塞尔方程,方程通解如下
| $ {{p_{1{\rm{D}}}}} \left ({r_{\rm{D}}},z \right ) = {X_1}{{\mathop{I}\nolimits} _0}\left({r_{\rm{D}}}\sqrt z \right) + {X_2}{{\mathop{ K}\nolimits} _0}\left ({r_{\rm{D}}}\sqrt z \right )$ | (5) |
| $ {{p_{2{\rm{D}}}}} \left({r_{\rm{D}}},z \right ) = {X_3}{{\mathop{I}\nolimits} _0}\left(\sqrt {{\rm{\sigma }}z} {r_{\rm{D}}}\right ) + {X_4}{{\mathop{K}\nolimits} _0}\left(\sqrt {{\rm{\sigma }}z} {r_{\rm{D}}} \right)$ | (6) |
式(5)、式(6)中的待定系数X1、X2、X3、X4 可由式(1)~ 式(4)确定。
将方程的通解代入定解条件,利用代入消元法求解得到拉氏空间的井底无因次压力[5-6]
| $ {{p_{{\rm{WD}}}}} = \dfrac{1}{z} \cdot \dfrac{1}{{{C_{\rm{D}}}z + \dfrac{1}{{S + \Psi (1,z)}}}}$ | (7) |
其中:
$\Psi ({r_{\rm{D}}},z) = \dfrac{{{\rm{\lambda }}{\Psi _{0,0}}(1,{\rm{\alpha }},\sqrt z ) + {\rm{\alpha }}\sqrt z {\Psi ^*}({\rm{\alpha }},z){\Psi _{0,1}}(1,{\rm{\alpha }},\sqrt z )}}{{\sqrt z [{\rm{\lambda }}{\Psi _{1,0}}(1,{\rm{\alpha }},\sqrt z ) + {\rm{\alpha }}\sqrt z {\Psi ^*}({\rm{\alpha }},z){\Psi _{1,1}}(1,{\rm{\alpha }},\sqrt z )]}}$;$\Psi({r_{\rm{D}}},z) = A/B$;$A{\rm{ = \lambda }}{\Psi_{0,0}}\left( {1,{\rm{\alpha }},\sqrt z } \right) + {\rm{\alpha }}\sqrt z {\Psi^*}\left( {{\rm{\alpha }},z} \right){\Psi_{0,1}}\left( {1,{\rm{\alpha }},\sqrt z } \right)$;$B{\rm{ = }}\sqrt z {\rm{\lambda }}{\Psi_{1,0}}\left( {1,{\rm{\alpha }},\sqrt z } \right) + \sqrt z {\rm{\alpha }}\sqrt z {\Psi^*}\left( {{\rm{\alpha }},z} \right){\Psi_{1,1}}\left( {1,{\rm{\alpha }},\sqrt z } \right)$;${\Psi_{m,n}}(\alpha ,\beta ,\gamma ) = {{\mathop{K}\nolimits} _m}(\alpha \gamma ){{\mathop{ I}\nolimits} _n}(\beta \gamma ) + {( - 1)^{m - n + 1}}{{\mathop{I}\nolimits} _m}(\alpha \gamma ){{\mathop{ K}\nolimits} _n}(\beta \gamma )$ (m = 0,1;n = 0,1)。
2 模型数值求解方法 2.1 Stehfest 数值反演对于拉氏空间的解,进行Laplace 解析反演较困难,由解析反演得到的解析解公式也是十分复杂,因此,文中采用的是Laplace 数值反演法,应用Stehfest 数值反演,得到拉氏空间解对应的实空间井底压力为[7-8]
| ${p_{\rm WD}}({t_{\rm D}}) = \dfrac{{\ln 2}}{{{t_{\mathop{\rm D}\nolimits} }}}\sum\limits_{i = 1}^N {{V_i} {{p_{\rm WD}}} } ({z_i})$ | (8) |
其中:
${z_i} = \dfrac{{\ln 2}}{{{t_{\rm D}}}}i$;${t_{\mathop{\rm D}\nolimits} } = \dfrac{{{{\mathop{K}\nolimits} _1}t}}{{{\phi _1}{\mu _1}{C_{{\mathop{\rm t}\nolimits} 1}}\mathop r\nolimits_{\mathop{\rm w}\nolimits} ^2 }}$;${V_i} = {\left( { - 1} \right)^{i + \frac{N}{2}}}\sum\limits_{k = \frac{{i + 1}}{2}}^{\min (i,\frac{N}{2})} {\dfrac{{{k^{\frac{N}{2} + 1}}(2k)!}}{{(\frac{{\mathop{N}\nolimits} }{2} - k)!{{(k!)}^2}(i - k)!(2k - i)!}}}$。
式(8)中,N 必须是偶数,经实践和对比,并综合考虑计算速度等因素,取N = 8。
2.2 虚宗量Bessel 函数的分段数值算法从式(8)可知,实空间井底压力的计算依赖于拉氏空间的井底无因次压力公式,并且从Laplace空间中的井底无因次压力公式(7)可以看出,虚宗量Bessel 函数的编程处理,关系到整个程序的运行速度和最终结果。若是采用积分算法会导致程序复杂,运行时间相对较长,计算精度不足会出现文献[9]、[10]中提到的曲线震荡情况,轻微震荡示意见图 1、图 2。
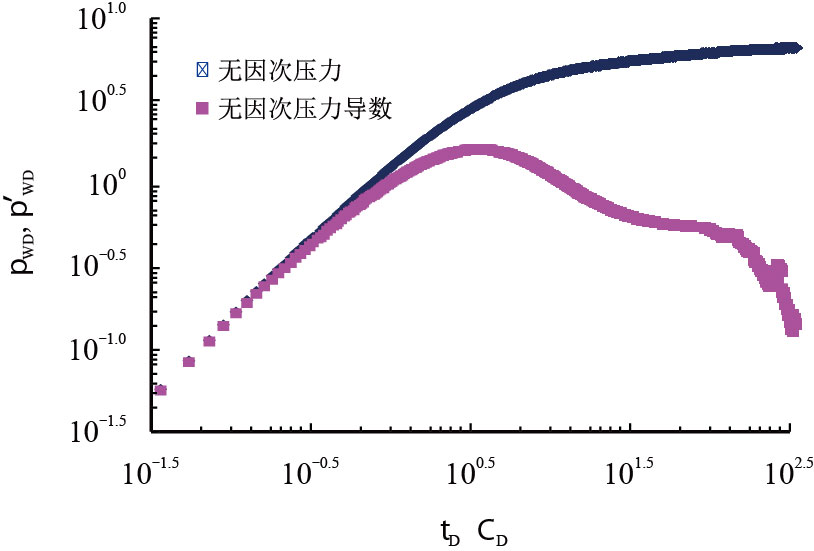 |
| 图1 示意图一 Fig. 1 Schematic diagram 1 |
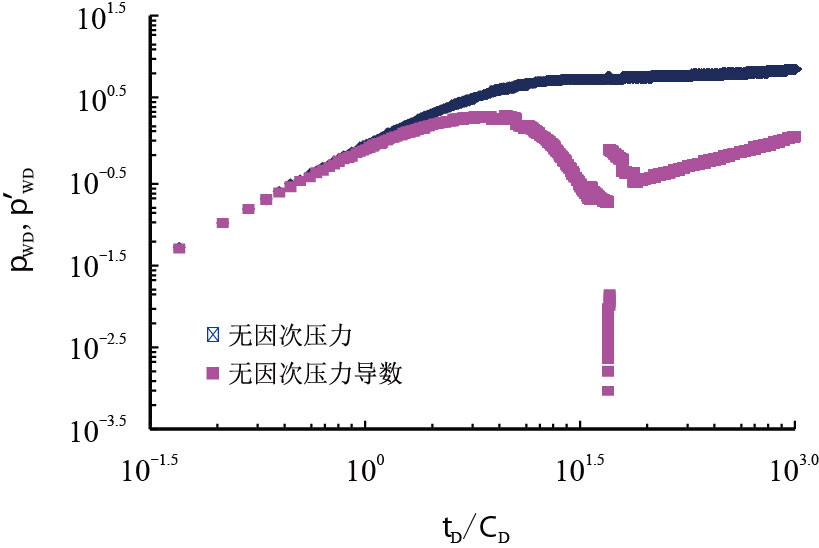 |
| 图2 示意图二 Fig. 2 Schematic diagram 2 |
曲线震荡对试井分析中后续的曲线拟合确定地层参数是非常不利的。因此,采用Bessel 函数分段数值算法(式(9)~ 式(12))进行数值计算[11-12],此种方法在计算将近834 d 计20 000 h 的井底无因次压力、井底无因次压力导数及对应的无因次时间共60 000 个数据时不足1 min 即可完成。
计算${I_0}()$,${I_1}()$,当$\left| r \right| < 3.75$时
| $\left\{ \begin{array}{l} {I_0}(r) = A(x)\\[3pt] {I_1}(r) = rB(x)\\[3pt] x = {\left( {\dfrac{r}{{3.75}}} \right)^2} \end{array} \right.$ | (9) |
当$\left| r \right| \geqslant 3.75$时
| $\left\{ \begin{array}{l} {I_0}(r) = \dfrac{{{{\rm{e}}^{\left| r \right|}}}}{{\sqrt {\left| r \right|} }}C(x)\\[3pt] {I_1}\left( {\left| r \right|} \right) = \dfrac{{{{\rm{e}}^{\left| r \right|}}}}{{\sqrt {\left| r \right|} }}D(x)\\[3pt] {I_1}\left( { - \left| r \right|} \right) = - {I_1}\left( {\left| r \right|} \right)\\[3pt] x = \dfrac{{3.75}}{{\left| r \right|}} \end{array} \right.$ | (10) |
计算${K_0}()$,${K_1}()$,当%$\left| r \right| $r \leqslant 2$时
| $\left\{ \begin{array}{l} {K_0}(r) = A(x) - {I_0}(r)\ln \dfrac{r}{2}\\[3pt] {K_1}(r) = \dfrac{1}{r}B(x) + {I_1}(r)\ln \dfrac{r}{2}\\[3pt] x = \dfrac{{{r^2}}}{4} \end{array} \right.$ | (11) |
当$r > 2$时
| $\left\{ \begin{array}{l} {K_0}(r) = \dfrac{{{{\rm{e}}^{ - r}}}}{{\sqrt r }}C(x)\\[3pt] {K_1}(r) = \dfrac{{{{\rm{e}}^{ - r}}}}{{\sqrt r }}D(x)\\[3pt] x = \dfrac{r}{2} \end{array} \right.$ | (12) |
其中:$A(x) = \sum\limits_{i = 0}^8 {{a_i}{x^i}} $;$B(x) = \sum\limits_{i = 0}^8 {{b_i}{x^i}} $;$C(x) = \sum\limits_{i = 0}^8 {{c_i}{x^i}} $;$D(x) = \sum\limits_{i = 0}^8 {{d_i}{x^i}} $。
虚宗量第j(j=1,2)类的Bessel函数的$a_i$,$b_i$,$c_i$,$d_i$的取值如表 1、表 2 所示。
| 表1 虚宗量第一类Bessel 函数的$a_i$,$b_i$,$c_i$,$d_i$的取值 Table 1 Value of $a_i$,$b_i$,$c_i$,$d_i$ of first Bessel function of imaginary argument |
| 表2 虚宗量第二类Bessel 函数的ai,bi,ci,di 的取值 Table 2 Value of ai,bi,ci,di of second Bessel function ofimaginary argument |
为说明上述虚宗量Bessel函数的分段数值算法的可行性和精确性,利用Matlab的虚宗量Bessel函数命令计算在$r=0.5,1.5,2.5,3.5$时${I _j}()$、${K _j}()$(j=0,1)的值,并与通过上述算法计算出来的值进行对比,结果见表 3。
| 表3 两种算法结果对比 Table 3 Comparison of results of two algorithms |
从表 3 数据可知,本文算法得出的结果与使用Matlab 虚宗量Bessel 函数命令得到的结果几乎完全吻合,证实了此种算法是精确可靠的,可广泛应用于实际工程计算。
3 结果分析在实际的试井分析中,压力导数双对数曲线给出的信息要比压力双对数曲线给出的信息更加清楚明显[13],因此,为了实际应用的需要,引入由Bourdet D 所给出的适用于压降试井的无因次压力导数基本公式,采用的压力导数表达式为pWD′ = dpWD/d ln(tD/CD),运用上述计算方法计算出在不同外边界条件下的压力和对应的压力导数值,得到试井曲线图(图 3~ 图 6),该图中的曲线平滑完整,没有出现曲线震荡情况,这使得试井分析中地层参数的获取更加精确可靠。
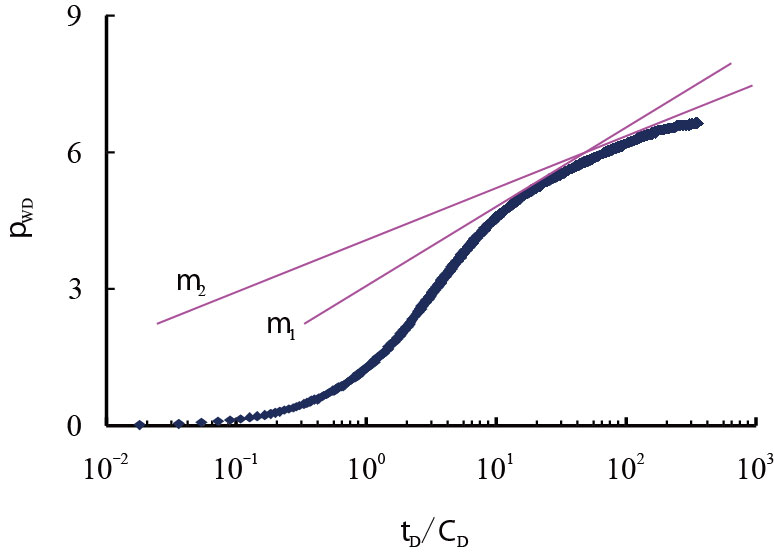 |
| 图3 复合油藏半对数曲线 Fig. 3 The semilog curves of composite reservoir |
图 3 是复合油藏无限大地层的半对数曲线,其中斜率m1 反映的是内区的地层特性参数,斜率m2反映的是外区的地层特性参数,m1/m2 则是窜流系数λ[14-15];这些特征在双对数线上会得到更明显的体现。
图 4 是${C_{\mathop{\rm D}\nolimits} }{{\rm{e}}^{2{\mathop{ S}\nolimits} }} = 1 000$,$\alpha = 1 000$,$\lambda=10$,$\sigma = 0.5$时的无限大地层的双对数曲线,易观察得压力导数曲线早期受井筒储集的影响,表现为斜率是1 的直线,接下来的驼峰表示过渡期,而后则是表示内区达到径向流的0.5 水平线,这些均是复合油藏压力导数曲线的典型特征[16-17]。
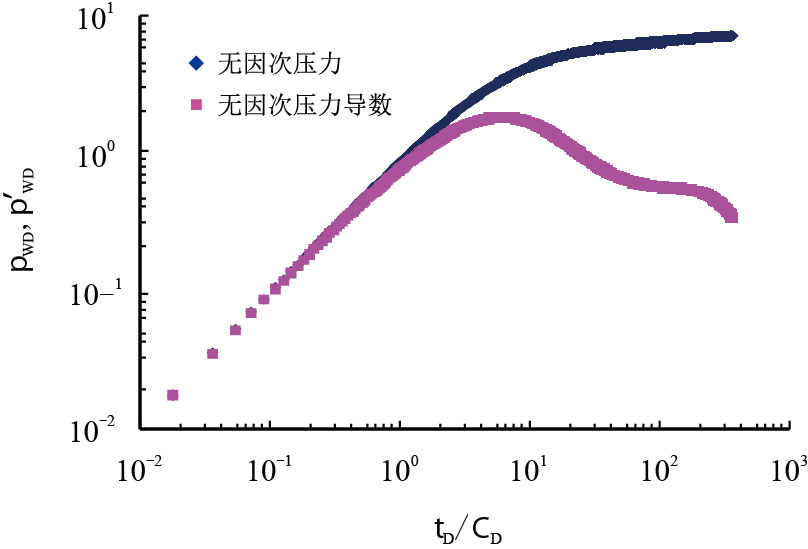 |
| 图4 无限大地层双对数曲线 Fig. 4 The double logarithmic curves of infinite formation |
图 5 的压力导数曲线中有压降稳定段出现,则说明定压稳定段出现,而后有压力导数趋于零且双对数曲线有剧陡性突降,则说明压降趋于稳定的特性已出现。
图 6 的双对数压力曲线和双对数导数曲线都上翘,表明的是全封闭油藏的典型特征[18-20]。
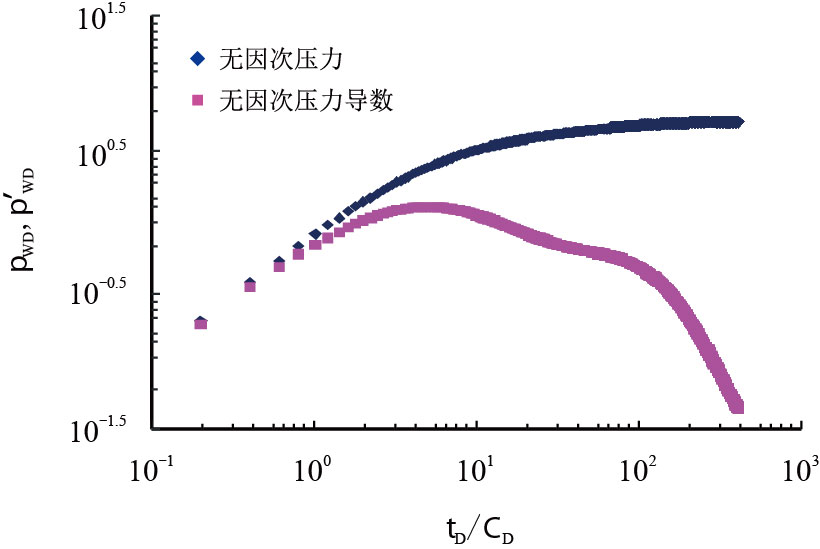 |
| 图5 定压边界的双对数曲线 Fig. 5 The double logarithmic curves of constant pressure boundary |
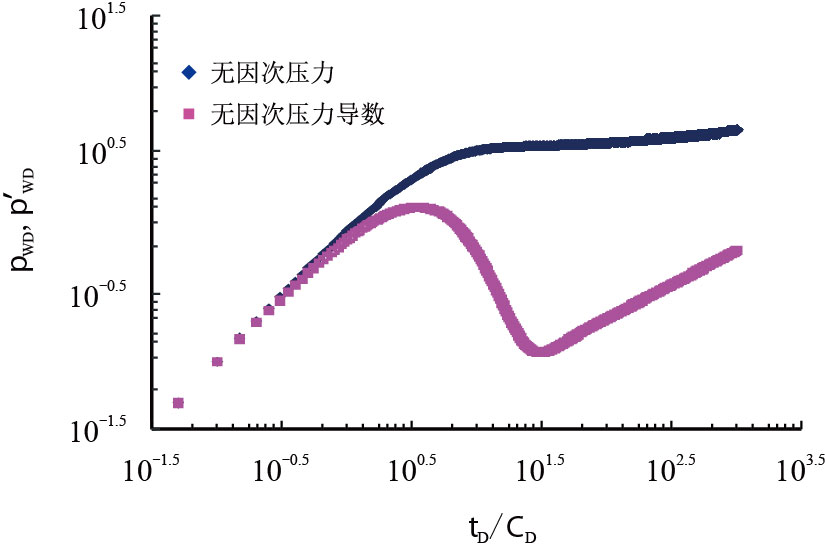 |
| 图6 封闭边界的双对数曲线 Fig. 6 The double logarithmic curves of closed boundary |
(1)采用的虚宗量Bessel 函数分段数值算法易于求解,且模型求解速度快,非常契合试井分析响应速度快的需求。
(2)该算法绘出的曲线平滑完整,没有因精度问题引起的曲线震荡的出现,给后续的试井分析带来了极大的便利。
致谢:本文受到研究生优质课程《数值分析》的资助,在此表示感谢。
符号说明${p_{1{\mathop{\rm D}\nolimits} }}$—内区无因次压力;
$r_{\rm{D}}$—无因次径向距离;
z—拉普拉斯变换变量,无因次;
$\alpha$—内外区交界面无因次半径;
${p_{2{\mathop{\rm D}\nolimits} }}$—外区无因次压力;
$\sigma$—弹性储容比,无因次;
$p_{\rm{WD}}$—无因次井底压力;
S—表皮系数,无因次;
$q_{\rm{D}}$—无因次产量;
$R_{\rm{D}}$—无因次到外边界距离;
$C_{\rm{D}}$—无因次井筒储集系数;
$K_1$—内区渗透率,mD;
h—储层厚度,m;
$q_{\rm{e}}$—参考产量,m3/d;
$\mu$—储层流体黏度,mPa$\cdot$s;
B—原油体积系数,m3/m3;
$p_{\rm{i}}$—原始地层压力,MPa;
$p_{\rm{1}}$—内区储层压力,MPa;
$K_2$—外区渗透率,mD;
$p_{\rm{2}}$—外区储层压力,MPa;
r—径向距离,m;
$r_{\rm{w}}$—井眼半径,m;
$\phi_1$—内区储层孔隙度,%;
$\phi_2$—外区储层孔隙度,%;
$\mu_1$—内区流体黏度,mPa$\cdot$s;
$\mu_2$—外区流体黏度,mPa$\cdot$s;
${C_{\rm t1}}$—内区综合压缩系数,MPa$^{-1}$;
${C_{\rm t2}}$—外区综合压缩系数,MPa$^{-1}$;
$p_{\rm{w}}$—井底压力,MPa;
q—产量,m3/d;
C—井筒储集系数,m3/MPa;
R—外边界距离,m;
${{\mathop{I}\nolimits} _j}()$,${{\mathop{K}\nolimits} _j}()$,(j = 0,1)— j阶的第一类、第二类虚宗量Bessel函数;
$\beta$,$\gamma$—参数,无因次;
${X_1}$、${X_2}$、${X_3}$、${X_4}$—待定系数,无因次;
$t_{\rm{D}}$—无因时间;
i—第i个区间;
N—区间数;
t—时间,h,
$a_i$,$b_i$,$c_i$,$d_i$—Bessel函数的系数;
$\lambda$—窜流系数,无因次;
$p_{\rm{WD}}^{\prime}$—无因次井底压力导数。
| [1] |
李全勇, 李顺初, 李伟, 等. 基于解相似结构的复合油藏渗流模型研究[J].
断块油气田, 2011, 18 (5) : 623 –625.
LI Quanyong, LI Shunchu, LI Wei, et al. Study on percolation model of composite media reservoir based on similar structure of solution[J]. Fault-Block Oil & Gas Field, 2011, 18 (5) : 623 –625. |
| [2] |
梁光跃, 廖新维, 赵晓亮. 特征点拟合法在非牛顿流试井解释中的应用[J].
西南石油大学学报(自然科学版), 2011, 33 (6) : 94 –99.
LIANG Guangyue, LIAO Xinwei, ZHAO Xiaoliang. Characteristic points matching method applied in nonnewtonian reservoir well testing[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33 (6) : 94 –99. |
| [3] |
梁尚斌, 王怒涛, 罗成栋, 等. 统一的油井试井解释模型及井底压力解[J].
西南石油学院学报, 2004, 26 (5) : 27 –29.
LIANG Shangbin, WANG Nutao, LUO Chengdong, et al. Unified oil well test interpretation model and bottom hole pressure solution[J]. Journal of Southwest Petroleum Institute, 2004, 26 (5) : 27 –29. |
| [4] |
李顺初, 郑鹏社, 张宇飞. 均质油气藏试井分析解的相似结构[J].
纯粹数学与应用数学, 2006, 22 (4) : 459 –463.
LI Shunchu, ZHENG Pengshe, ZHANG Yufei. The similar structure of pressure distribution in the homogenous reservoir[J]. Pure and Applied Mathematics, 2006, 22 (4) : 459 –463. |
| [5] |
李顺初, 郑鹏社, 张宇飞. 复合油藏试井分析解的相似结构[J].
数学的实践与认识, 2008, 38 (3) : 23 –28.
LI Shunchu, ZHENG Pengshe, ZHANG Yufei. The similar structure of pressure distribution in the composite reservoir[J]. Mathematics in Practice and Theory, 2008, 38 (3) : 23 –28. |
| [6] |
李顺初, 刘平礼, 赵立强. 复合油藏中的不同边界条件下的井底压力分析[J].
西南石油学院学报, 2002, 24 (5) : 32 –33.
LI Shunchu, LIU Pingli, ZHAO Liqiang. The analysis of bottom pressure in complex reservoir with different boundary conditions[J]. Journal of Southwest Petroleum Institute, 2002, 24 (5) : 32 –33. |
| [7] |
卢德唐.
现代试井理论及应用[M]. 北京: 石油工业出版社, 2009 .
LU Detang. Theory and application of modern well testing[M]. Beijing: Petroleum Industry Press, 2009 . |
| [8] |
万小勇, 杨利萍, 龙武, 等. 塔河碎屑岩注水井试井解释的一种新方法[J].
石油天然气学报, 2013, 35 (9) : 105 –108.
WAN Xiaoyong, YANG Liping, LONG Wu, et al. A method of well test in clastic water injection wells in Tahe Oilfield[J]. Journal of Oil and Gas Technology, 2013, 35 (9) : 105 –108. |
| [9] |
李季, 李素. 提高低速非达西渗流模型求解精度的一种方法[J].
中国石油和化工标准与质量, 2013 (7) : 108 –109.
LI Ji, LI Su. A method of improving solving accuracy of the low-speed non-darcy seepage model[J]. China Petroleum and Chemistry Standard and Quality, 2013 (7) : 108 –109. |
| [10] |
WANG Chao. A study of well test analysis method in waterflood development reservoir performance[D]. Xi'an:Xi'an Shiyou University, 2011.
王超. 注水开发油藏动态分析方法研究[D]. 西安:西安石油大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10705-1012493562.htm |
| [11] |
徐士良.
C常用数值算法集[M]. 北京: 清华大学出版社, 1996 .
XU Shiliang. The common numerical algorithm set of C language[M]. Bejing: Tsinghua University Press, 1996 . |
| [12] |
Press W H, Teukolsky S A, Teokulsky W T, Vetterling W T,et al. Numerical recipes in C[M]. 2nd ed. Translated by FU Zuyun. Bejing:Publishing House of Electronics Industry, 1995.
Press W H, Teokulsky W T, Vetterling B P. C语言数值算法程序大全[M]. 2版. 傅祖芸,译. 北京:电子工业出版社, 1995. |
| [13] | Issaka M B, Ambastha A K. A generalized pressure derivative analysis for composite reservoirs[J]. Journal of Canadian Petroleum Technology, 1999, 38 (13) : 59 . |
| [14] |
方甲中, 程林松, 任胜利, 等. 动边界复合油藏低速非达西渗流试井分析[J].
西南石油大学学报(自然科学版), 2011, 33 (5) : 104 –108.
FANG Jiazhong, CHENG Linsong, REN Shengli, et al. Well test analysis of low velocity and non-Darcy flow in composite reservoir with dynamic boundary[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33 (5) : 104 –108. |
| [15] |
石国新, 聂仁仕, 路建国, 等. 2区复合油藏水平井试井模型与实例解释[J].
西南石油大学学报(自然科学版), 2012, 34 (5) : 99 –106.
SHI Guoxin, NIE Renshi, LU Jianguo, et al. Well test model of horizontal well in 2-zoned composite reservoir and example interpretation[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34 (5) : 99 –106. |
| [16] |
蔡明金, 张福祥, 彭建新, 等. 复合油藏内外区同时压裂试井模型研究[J].
石油化工应用, 2013, 32 (4) : 13 –16.
CAI Mingjin, ZHANG Fuxiang, PENG Jianxin, et al. Well test analysis on single well with a vertical fracture in composite reservoir considering inner and exterior zone fracturing[J]. Petrochemical Industry Application, 2013, 32 (4) : 13 –16. |
| [17] |
刘义坤, 闫宝珍, 翟云芳, 等. 均质复合油藏试井分析方法[J].
石油学报, 1994, 15 (1) : 92 –100.
LIU Yikun, YAN Baozhen, ZHAI Yunfang, et al. Transient pressure behavoir homogeneous composite reservoir[J]. Acta Petrolei Sinica, 1994, 15 (1) : 92 –100. |
| [18] |
刘柏峰, 柳阳明, 陈伟, 等. 基于边界元法的串珠状油藏压力动态分析[J].
西南石油大学学报(自然科学版), 2009, 31 (4) : 127 –130.
LIU Baifeng, LIU Yangming, CHEN Wei, et al. Pressure dynamic analysis of beads shaped reservoir based on boundary element method[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31 (4) : 127 –130. |
| [19] |
王建忠, 姚军. 变渗透率条件下低渗介质非稳态压力变化特征[J].
西安石油大学学报(自然科学版), 2013, 28 (5) : 57 –61.
WANG Jianzhong, YAO Jun. Transient pressure characteristics of low-permeability media under variable permeability[J]. Journal of Xi'an Shiyou University (National Science Edition), 2013, 28 (5) : 57 –61. |
| [20] |
丘永新, 庄惠农. 复合油藏压力曲线在双对数综合图上的特征及实例分析[J].
油气井测试, 1992, 1 (3) : 16 –20.
QIU Yongxin, ZHUANG Huinong. The characteristic on Log-log plots for pressure curves of composite system and its case study[J]. Well Testing, 1992, 1 (3) : 16 –20. |
 2016, Vol. 38
2016, Vol. 38


