2. 中国石油塔里木油田分公司勘探开发研究院测井中心, 新疆 库尔勒 841000;
3. 中国石油西南油气田公司重庆气矿, 重庆 江北 400021
2. Well Logging Center, Exploration and Development Research Institute, Tarim Oilfield, PetroChina, Korla, Xinjiang 841000, China;
3. Chongqing Division of Southwest Oil & Gas Field Company, PetroChina, Jiangbei, Chongqing 400021, China
目前关于压裂井渗流模型的研究已比较成熟,其主要包括:双线性流模型[1]、二维平面模型[2-3]、三线性流模型[4-6] 和椭圆流模型[7-8]。低渗透地层的一个显著特征就是存在启动压力梯度,流体在一定启动压力下才能流动[9-11],一些学者研究了考虑启动压力梯度影响的压裂井渗流模型,但均未考虑各种矩形复合边界的影响[12-15]。而目前对于压裂井各种矩形复合边界影响的研究主要有利用镜像反映原理进行叠加的方法[16-17]和基于压裂井三线性流推导的矩形封闭边界模型[15],前者由于考虑启动压力梯度后的方程十分复杂,应用叠加原理将存在困难;后者是基于完全对称的1/4 象限推导得到的理想情形——只能描述在垂直于裂缝和平行于裂缝两个方向上分别具有完全对称的不渗透边界影响的情形,并且也未考虑启动压力梯度的影响。目前尚未见有关考虑启动压力梯度和各种非对称边界影响的压裂井渗流模型的相关研究。针对这一问题,本文研究了低渗透压裂井非对称区域三线性渗流新模型,与传统的理想对称区域模型相比,新模型考虑了更为复杂的模型条件—— 启动压力梯度的影响和各种非对称边界的组合,因此,基于完全对称的1/4象限的模型分析方法已不能用于非对称区域渗流模型,本文提出了基于非对称的整个区域的模型分析新方法。
1 渗流模型的建立与求解 1.1 物理模型传统的压裂井三线性流模型考虑不渗透边界影响[5] 的流动示意图如图 1所示,流体在垂直裂缝与地层中形成三线性流,形成3个流动区域:裂缝线性流区、垂直于裂缝的线性流区、平行于裂缝的线性流区。因为传统模型是基于完全对称的1/4 象限推导的,所以只能描述在垂直于裂缝和平行于裂缝两个方向上分别具有完全对称的不渗透边界影响的情形。
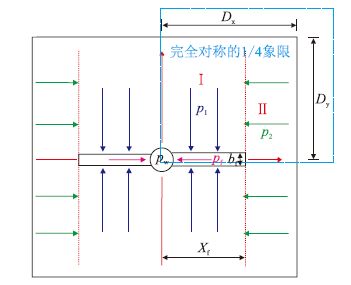 |
| 图1 传统的压裂井三线性流模型考虑不渗透边界影响的流动示意图 Fig. 1 Schematic diagram of the traditional trilinear-flow model of fractured well influenced by impermeable boundary |
本文研究的压裂井非对称区域三线性渗流物理模型示意图如图 2 所示:(1) 在水平面内流动区域为非对称的四象限区域:第一象限,1-1$'$区域;第二象限,2-2$'$区域;第三象限,3-3$'$区域;第四象限,4-4$'$区域;(2) 流体在水平面内做三线性流动:第一线性流,在压裂裂缝右翼f$_1$和左翼f$_2$区内做线性流;第二线性流,在垂直于裂缝的1、2、3、4地层区内做线性流;第三线性流,在平行于裂缝的1$'$、2$'$、3$'$、4$'$地层区内做线性流;(3) 储层在水平面内4 个方向上的外边界到井距离不等,可以是封闭或无穷大边界(针对传统模型,这里只考虑这两种边界的影响)。此外,模型还考虑以下条件:(1) 考虑启动压力梯度的低速非达西渗流模式;(2) 储层顶底为不渗透边界;(3) 岩石和流体均微可压缩,且压缩系数为常数;(4) 裂缝以井轴对称,等距离分布,裂缝高度和油层厚度相等;(5) 沿着裂缝方向存在压力降,裂缝末端无流体通过;(6) 忽略重力,地层流体进入井筒仅经由裂缝。
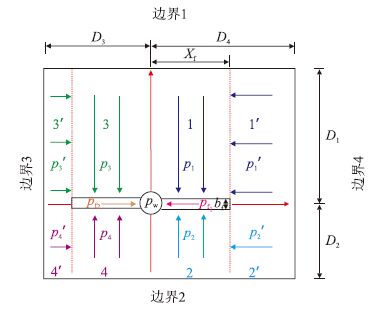 |
| 图2 压裂井非对称区域三线性渗流物理模型流动示意图 Fig. 2 Schematic diagram of a trilinear-flow model of fractured well on asymmetric regions |
严格描述整条裂缝中流体渗流问题的控制方程组可以写为
| $\dfrac{{\partial ^2 p_{{\rm{f}}_{\rm{1}} } }}{{\partial x^2 }} + \dfrac{{\partial ^2 p_{{\rm{f}}_{\rm{1}} } }}{{\partial y^2 }} = \dfrac{{\phi _{\rm{f}} \mu C_{{\rm{ft}}} }}{3.6{K_{\rm{f}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} } }}{{\partial t}}\begin{array}{*{20}c} {} & {(0 \leqslant x \leqslant X_{\rm{f}} ,- b_{\rm{f}} /2 \leqslant y \leqslant b_{\rm{f}} /2)} \\ \end{array}$ | (1) |
| $\dfrac{{\partial ^2 p_{{\rm{f}}_{\rm{2}} } }}{{\partial x^2 }} + \dfrac{{\partial ^2 p_{{\rm{f}}_{\rm{2}} } }}{{\partial y^2 }} = \dfrac{{\phi _{\rm{f}} \mu C_{{\rm{ft}}} }}{3.6{K_{\rm{f}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } }}{{\partial t}}\begin{array}{*{20}c} {} & {( - X_{\rm{f}} \leqslant x \leqslant 0,- b_{\rm{f}} /2 \leqslant y \leqslant b_{\rm{f}} /2)} \\ \end{array}$ | (2) |
初始条件
| $p_{{\rm{f}}_{\rm{1}} } (x,y,t) = p_{{\rm{f}}_{\rm{2}} } (x,y,t) = p_{\rm{i}}$ | (3) |
缝端封闭条件
| $\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} } (X_{\rm{f}} ,y,t)}}{{\partial x}} = \dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } ( - X_{\rm{f}} ,y,t)}}{{\partial x}} = 0$ | (4) |
裂缝面与储层流量相等条件为
| $\dfrac{{K_{\rm{f}} }}{\mu }\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} } (x,b_{\rm{f}} /2,t)}}{{\partial y}} = \dfrac{K}{\mu }\dfrac{{\partial p_1 (x,b_{\rm{f}} /2,t)}}{{\partial y}}$ $\dfrac{{K_{\rm{f}} }}{\mu }\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} } (x,- b_{\rm{f}} /2,t)}}{{\partial y}} = \dfrac{K}{\mu }\dfrac{{\partial p_2 (x,- b_{\rm{f}} /2,t)}}{{\partial y}}$ | (5) |
| $\dfrac{{K_{\rm{f}} }}{\mu }\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } (x,b_{\rm{f}} /2,t)}}{{\partial y}} = \dfrac{K}{\mu }\dfrac{{\partial p_1 (x,b_{\rm{f}} /2,t)}}{{\partial y}}$ $\dfrac{{K_{\rm{f}} }}{\mu }\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } (x,- b_{\rm{f}} /2,t)}}{{\partial y}} = \dfrac{K}{\mu }\dfrac{{\partial p_2 (x,- b_{\rm{f}} /2,t)}}{{\partial y}}$ | (7) |
井底压力条件(左半条裂缝和右半条裂缝在井底压力相等)
| $p_{{\rm{f}}_{\rm{1}} } (0,y,t) = p_{{\rm{f}}_{\rm{2}} } (0,y,t)$ | (9) |
井底流量条件(左半条裂缝和右半条裂缝井底流量相加等于总流量)
| $\dfrac{{K_{\rm{f}} h}}{\mu }\left[{\int_{ - b_{\rm{f}} /2}^{b_{\rm{f}} /2} {\dfrac{{\partial p_{{\rm{f}}_1 } (0,y,t)}}{{\partial x}}{\rm{d}}y} + \int_{ - b_{\rm{f}} /2}^{b_{\rm{f}} /2} {\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } (0,y,t)}}{{\partial x}}{\rm{d}}y} } \right] = \\ \dfrac{1}{{86.4}}qB + \dfrac{{C_{\rm{w}} }}{{3.6}}\dfrac{{\partial p_{\rm{w}} }}{{\partial t}}$ | (10) |
相对于传统的裂缝渗流方程,这里考虑了整个裂缝区域($-X_{\rm{f}}\leqslant x\leqslant X_{\rm{f}}$,$-b_{\rm{f}}/2\leqslant y\leqslant b_{\rm{f}}/2$),并且在井底满足左半条裂缝和右半条裂缝压力相等和流量之和等于总流量。
考虑到与井泄油面积相比裂缝尺寸比较小,利用裂缝面与储集层流量相等的条件,对裂缝方程沿裂缝方向积分平均化[18],可建立定产量生产条件下的整条裂缝线性流模型,即
$0\leqslant x\leqslant X_{\rm{f}}$ 时
| $\dfrac{{{\rm{d}}^2 p_{{\rm{f}}_{\rm{1}} } }}{{{\rm{d}}x^2 }} + \dfrac{K}{{b_{\rm{f}} K_{\rm{f}} }}\left( {\dfrac{{{\rm{d}}p_1 }}{{{\rm{d}}y}}|_{y = b_{\rm{f}} /2} + \dfrac{{{\rm{d}}p_2 }}{{{\rm{d}}y}}|_{y = - b_{\rm{f}} /2} } \right) = \\ \dfrac{{\phi _{\rm{f}} \mu C_{{\rm{ft}}} }}{3.6{K_{\rm{f}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} } }}{{\partial t}}$ | (11) |
$-X_{\rm{f}}\leqslant x\leqslant 0$时
| $\dfrac{{{\rm{d}}^2 p_{{\rm{f}}_2 } }}{{{\rm{d}}x^2 }} + \dfrac{K}{{b_{\rm{f}} K_{\rm{f}} }}\left( {\dfrac{{{\rm{d}}p_3 }}{{{\rm{d}}y}}|_{y = b_{\rm{f}} /2} + \dfrac{{{\rm{d}}p_4 }}{{{\rm{d}}y}}|_{y = - b_{\rm{f}} /2} } \right) = \\ \dfrac{{\phi _{\rm{f}} \mu C_{{\rm{ft}}} }}{3.6{K_{\rm{f}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} } }}{{\partial t}}$ | (12) |
在地层渗流中,考虑在平行于裂缝和垂直于裂缝两个地层渗流阶段都存在启动压力梯度的影响,由流体的运动方程、状态方程及连续性方程,可推导出单相微可压缩流体单向流动的低速非达西渗流微分方程[13]
| $\dfrac{{\partial ^2 p}}{{\partial x^2 }} - \lambda _{\rm{B}} C_\rho \dfrac{{\partial p}}{{\partial x}} = \dfrac{{\phi \mu C_{\rm{t}} }}{3.6K}\dfrac{{\partial p}}{{\partial t}}$ | (13) |
引入以下无因次量
无因次裂缝压力
| $p_{{\rm{f}}_j {\rm{D}}} = \dfrac{{K_{\rm{f}} h}}{{1.842 \times 10^{ - 3} qB\mu }}(p_{\rm{i}} - p_{{\rm{f}}_j } )$,$j=1,2$ |
无因次地层压力(1,2,3,4区)
| $p_{j{\rm{D}}} = \dfrac{{Kh}}{{1.842 \times 10^{ - 3} qB\mu }}(p_{\rm{i}} - p_j )$ |
无因次地层压力(1$'$,2$'$,3$'$,4$'$区)
| $p_{j'{\rm{D}}} = \dfrac{{Kh}}{{1.842 \times 10^{ - 3} qB\mu }}(p_{\rm{i}} - p_{j'} )$,$j=1,2,3,4$ |
无因次井底压力
| $p_{{\rm{wD}}} = \dfrac{{Kh}}{{1.842 \times 10^{ - 3} qB\mu }}(p_{\rm{i}} - p_{\rm{w}} )$ |
无因次时间
| $t_{{\rm{D}}x_{\rm{f}} } = \dfrac{{3.6Kt}}{{\phi \mu C_{\rm{t}} X_{\rm{f}}^2 }}$ |
无因次裂缝扩散系数
| $\eta _{{\rm{fD}}} = \dfrac{{K_{\rm{f}} \phi C_{\rm{t}}^{} }}{{K\phi _{\rm{f}} C_{{\rm{ft}}} }}$ |
无因次井筒储集系数
| $S_{{\rm{wfD}}} = \dfrac{{C_{\rm{w}} }}{{2\pi \phi C_{\rm{t}} hX_{\rm{f}}^2 }}$ |
无因次距离、宽度
| $x_{\rm{D}} = \dfrac{x}{{X_{\rm{f}} }}$ |
| $y_{\rm{D}} = \dfrac{y}{{X_{\rm{f}} }}$ |
| $b_{\rm{D}} = \dfrac{{b_{\rm{f}} }}{{X_{\rm{f}} }}$ |
无因次边界距离
| $D_{j{\rm{D}}} = \dfrac{{D_j }}{{X_{\rm{f}} }}~~~~j=1,2,3,4$ |
| $D_{x{\rm{D}}} = \dfrac{{D_x }}{{X_{\rm{f}} }}$ |
| $D_{y{\rm{D}}} = \dfrac{{D_y }}{{X_{\rm{f}} }}$ |
无因次启动压力梯度
| $M_{\rm{D}} = \lambda _{\rm{B}} C_\rho X_{_{\rm{f}} }^{}$ |
无因次裂缝导流
| $C_{{\rm{fD}}} = \dfrac{{K_{\rm{f}} b_{\rm{f}} }}{{KX_{\rm{f}} }}$ |
基于上述的无因定义,可以得到考虑启动压力梯度影响的低渗透压裂井非对称区域三线性渗流模型无因次数学模型。
(1) 裂缝渗流方程
$0 \leqslant x_{\rm{D}} \leqslant 1,- b_{\rm{D}} /2 \leqslant y_{\rm{D}} \leqslant b_{\rm{D}} /2$
| $\dfrac{{{\rm{d}}^2 p_{{\rm{f}}_{\rm{1}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}}^2 }} + \dfrac{1}{{C_{{\rm{fD}}} }}\left( {\dfrac{{{\rm{d}}p_{{\rm{1D}}} }}{{{\rm{d}}y_{\rm{D}} }}|_{y_{\rm{D}} = b_{\rm{D}} /2} + \dfrac{{{\rm{d}}p_{{\rm{2D}}} }}{{{\rm{d}}y_{\rm{D}} }}|_{y_{\rm{D}} = - b_{\rm{D}} /2} } \right) = \dfrac{1}{{\eta _{{\rm{fD}}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{1}} {\rm{D}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}$ | (14) |
$ - 1 \leqslant x_{\rm{D}} \leqslant 0,- b_{\rm{D}} /2 \leqslant y_{\rm{D}} \leqslant b_{\rm{D}} /2$
| $\dfrac{{{\rm{d}}^2 p_{{\rm{f}}_{\rm{2}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}}^2 }} + \dfrac{1}{{C_{{\rm{fD}}} }}\left( {\dfrac{{{\rm{d}}p_{3{\rm{D}}} }}{{{\rm{d}}y_{\rm{D}} }}|_{y_{\rm{D}} = b_{\rm{D}} /2} + \dfrac{{{\rm{d}}p_{4{\rm{D}}} }}{{{\rm{d}}y_{\rm{D}} }}|_{y_{\rm{D}} = - b_{\rm{D}} /2} } \right) = \dfrac{1}{{\eta _{{\rm{fD}}} }}\dfrac{{\partial p_{{\rm{f}}_{\rm{2}} {\rm{D}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}$ | (15) |
| $\dfrac{{{\rm{d}}p_{{\rm{f}}_{\rm{1}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}} }}|_{x_{\rm{D}} = 1} = \dfrac{{{\rm{d}}p_{{\rm{f}}_{\rm{2}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}} }}|_{x_{\rm{D}} = - 1} = 0$ | (16) |
| $\left. {p_{{\rm{f}}_{\rm{1}} {\rm{D}}} } \right|_{x_{\rm{D}} = 0} = \left. {p_{{\rm{f}}_{\rm{2}} {\rm{D}}} } \right|_{x_{\rm{D}} = 0}$ | (17) |
| $\dfrac{{{\rm{d}}p_{{\rm{f}}_{\rm{1}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}} }}|_{x_{\rm{D}} = 0} + \dfrac{{{\rm{d}}p_{{\rm{f}}_{\rm{2}} {\rm{D}}} }}{{{\rm{d}}x_{\rm{D}} }}|_{x_{\rm{D}} = 0} = - \dfrac{{2\pi }}{{C_{{\rm{fD}}} }}\left( {1 - S_{{\rm{wfD}}} \dfrac{{\partial p_{{\rm{wD}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}} \right) $ | (18) |
(2) 储层渗流方程
①油藏中的流动,平行于裂缝方向指向井筒的流动
右半区域($j=1,2$):$1 \leqslant x_{\rm{D}} \leqslant D_{{\rm{4D}}}$
左半区域($j=3,4$):$D_{{\rm{3D}}} \leqslant x_{\rm{D}} \leqslant - 1$
| $\dfrac{{\partial ^2 p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}}^2 }} - M_{\rm{D}} \dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}} }} = \dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}$ | (19) |
边界条件
右半区域($j=1,2$)
| $p_{j'{\rm{D}}(1,t_{{\rm{D}}x_{\rm{f}} } )} = p_{j{\rm{D}}(1,t_{{\rm{D}}x_{\rm{f}} } )}$ | (20) |
| $\mathop {\lim }\limits_{x_{\rm{D}} \to \infty } p_{j'{\rm{D}}} = 0~~~~~~无穷边界$ | (21) |
| $\left. {\dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}} }}} \right|_{x_{\rm{D}} = D_{{\rm{4D}}} } = 0~~~~~~封闭边界$ | (22) |
左半区域($j=3,4$)
| $p_{j'{\rm{D}}( - 1,t_{{\rm{D}}x_{\rm{f}} } )} = p_{j{\rm{D}}( - 1,t_{{\rm{D}}x_{\rm{f}} } )}$ | (23) |
| $\mathop {\lim }\limits_{x_{\rm{D}} \to - \infty } p_{j'{\rm{D}}} = 0~~~~~~无穷边界$ | (24) |
| $\left. {\dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}} }}} \right|_{x_{\rm{D}} = D_{{\rm{3D}}} } = 0~~~~~~封闭边界$ | (25) |
初始条件
| $p_{j'} |_{t_{{\rm{D}}x_{\rm{f}} } = 0} = 0~~~~~~j = 1,2,3,4$ | (26) |
②油藏中的流动,垂直于裂缝方向的流动
右半区域($j=1,2$):$0 \leqslant x_{\rm{D}} \leqslant 1$
右上区域(j=1):$b_{\rm{D}} /2 \leqslant y_{\rm{D}} < D_{{\rm{1D}}} $
右下区域(j=2):$ - D_{{\rm{2D}}} \leqslant y_{\rm{D}} < - b_{\rm{D}} /2$
| $\dfrac{{\partial ^2 p_{j{\rm{D}}} }}{{\partial y_{\rm{D}}^2 }} - M_{\rm{D}} \dfrac{{\partial p_{j{\rm{D}}} }}{{\partial y_{\rm{D}} }} + \dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}} }}|_{(1,t_{{\rm{D}}x_{\rm{f}} } )} = \dfrac{{\partial p_{j{\rm{D}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}$ | (27) |
左半区域(j=3,4):${\rm{ - }}1 \leqslant x_{\rm{D}} \leqslant 0$
左上区域($j=3$):$b_{\rm{D}} /2 \leqslant y_{\rm{D}} < D_{{\rm{1D}}} $
左下区域($j=4$):$ - D_{{\rm{2D}}} \leqslant y_{\rm{D}} < - b_{\rm{D}} /2$
| $\dfrac{{\partial ^2 p_{j{\rm{D}}} }}{{\partial y_{\rm{D}}^2 }} - M_{\rm{D}} \dfrac{{\partial p_{j{\rm{D}}} }}{{\partial y_{\rm{D}} }} + \dfrac{{\partial p_{j'{\rm{D}}} }}{{\partial x_{\rm{D}} }}|_{( - 1,t_{{\rm{D}}x_{\rm{f}} } )} = \dfrac{{\partial p_{j{\rm{D}}} }}{{\partial t_{{\rm{D}}x_{\rm{f}} } }}$ | (28) |
边界条件
上半区域(j=1,3)
| $p_{{\rm{f}}_1 {\rm{D}}(b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} = p_{j{\rm{D}}(b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} \dfrac{2}{\pi }S_{\rm{f}} \dfrac{{\partial p_{j{\rm{D}}(b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} }}{{\partial y_{\rm{D}} }}|_{y_{\rm{D}} = b_{\rm{D}} /2}$ | (29) |
| $p_{j{\rm{D}}} |_{(y_{\rm{D}} \to \infty )} = 0$ | (30) |
| $\left. {\dfrac{{\partial p_{j{\rm{D}}} }}{{\partial x_{\rm{D}} }}} \right|_{x_{\rm{D}} = D_{1{\rm{D}}} } = 0$ | (31) |
下半区域(j=2,4)
| $p_{{\rm{f}}_{\rm{1}} {\rm{D}}( - b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} = p_{j{\mathop{\rm D}\nolimits} ( - b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} -\dfrac{2}{\pi}S_{\rm{f}} \dfrac{{\partial p_{j{\rm{D}}( - b_{\rm{D}} /2,t_{{\rm{D}}x_{\rm{f}} } )} }}{{\partial y_{\rm{D}} }}|_{y_{\rm{D}} = - b_{\rm{D}} /2}$ | (32) |
| $p_{j{\rm{D}}} |_{(y_{\rm{D}} \to - \infty )} = 0$ | (33) |
| $\left. {\dfrac{{tial p_{j{\rm{D}}} }}{{tial x_{\rm{D}} }}} \right|_{x_{\rm{D}} = D_{{\rm{2D}}} } = 0$ | (34) |
初始条件
| $p_{j{\rm{D}}} |_{t_{{\rm{D}}x_{\rm{f}} } = 0} = 0~~~~~~j=1,2,3,4$ | (35) |
对式(14)$\sim$(35) 进行Laplace 变换后联立求解可得到井底压力在拉普拉斯空间的表达式
| $\bar p_{{\rm{wD}}}\!=\!\dfrac{{2\beta }}{{\dfrac{1}{s}\left\{{2\beta sS_{{\rm{wfD}}}\!-\!\left[{\dfrac{{({\rm{e}}^{\!-\!2\psi _{\rm{1}} }\!-\!1)}}{{1\!+\!{\rm{e}}^{\!-\!2\psi_{\rm{1}}}}}\psi _{\rm{1}}\!+\!\dfrac{{({\rm{e}}^{\!-\!2\psi_{\rm{2}} }\!-\!1)}}{{(1\!+\!{\rm{e}}^{\!-\!2\psi _{\rm{2}}})}}\psi _{\rm{2}}}\right]}\right\}}} $ | (36) |
式中:
| $\psi _{\rm{1}} = \left[{\dfrac{s}{{\eta _{{\rm{fD}}} }} - \dfrac{1}{{C_{{\rm{fD}}} }}\dfrac{{(A_{\rm{1}} + A_{\rm{2}} - 2)\pi }}{{2S_{\rm{f}} }}} \right]^{1/2}~~~~(右半裂缝)$ |
| $\psi _{\rm{2}} = \left[{\dfrac{s}{{\eta _{{\rm{fD}}} }} - \dfrac{1}{{C_{{\rm{fD}}} }}\dfrac{{(A_{\rm{1}} + A_{\rm{2}} - 2)\pi }}{{2S_{\rm{f}} }}} \right]^{1/2}~~~~(左半裂缝)$ |
| $\beta = \dfrac{\pi }{{C_{{\rm{fD}}} }}$ |
边界1和边界2($n=1,2$)
| $A_n = \dfrac{{ - \pi }}{{2R_2 S_{\rm{f}} - \pi }}~~~~~无穷$ |
| $A_n = \dfrac{{\left\{ {\dfrac{1}{{R_2 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(D_{n{\rm{D}}} - b_{\rm{D}} )} } \right]}} + \dfrac{1}{{R_1 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(b_{\rm{D}} - D_{n{\rm{D}}} )} } \right]}}} \right\}}}{{\left\{ {\dfrac{1}{{R_2 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(D_{n{\rm{D}}} - b_{\rm{D}} )} } \right]}} + \dfrac{1}{{R_1 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(b_{\rm{D}} - D_{n{\rm{D}}} )} } \right]}}} \right\} - \dfrac{{2S_{\rm{f}} }}{\pi }}}~~~~~封闭$ |
| $R_1 = \dfrac{{M_{\rm{D}} + \sqrt {M_{\rm{D}} ^2 + 4(s - B)} }}{2}$ |
| $R_2 = \dfrac{{M_{\rm{D}} - \sqrt {M_{\rm{D}} ^2 + 4(s - B)} }}{2}$ |
边界3和4($n=3,4$)
| $B = r_2 ~~~~~无穷$ |
| $B{\rm{ = }} {\dfrac{{r_2 r_1 \left[{{\rm{e}}^{(r_2 - r_1 )D_{n{\rm{D}}} + r_1 } - {\rm{e}}^{r_2 } } \right]}}{{r_2 {\rm{e}}^{(r_2 - r_1 )D_{n{\rm{D}}} + r_1 } - r_1 {\rm{e}}^{r_2 } }}} ~~~~~封闭$ |
| $r_1 = \dfrac{{M_{\rm{D}} + \sqrt {M_{\rm{D}} ^2 + 4s} }}{2}$ |
| $r_2 = \dfrac{{M_{\rm{D}} - \sqrt {M_{\rm{D}} ^2 + 4s} }}{2}$ |
若令式(36) 中$D_{1{\rm{D}}} = D_{2{\rm{D}}} = D_{y{\rm{D}}} $,$D_{{\rm{3D}}} = D_{{\rm{4D}}} = D_{x{\rm{D}}} $,即可得到传统的压裂井三线性流矩形封闭模型的井底压力在拉普拉斯空间中的表达式
| $\bar p_{{\rm{wD}}} = \dfrac{\beta }{{s\left( {\psi \tanh \psi + \beta sS_{{\rm{wfD}}} } \right)}}$ | (37) |
式中:
| $\psi = \left[{\dfrac{s}{{\eta _{{\rm{fD}}} }} - \dfrac{2}{{C_{{\rm{fD}}} }}\dfrac{{(A - 1)\pi }}{{2S_{\rm{f}} }}} \right]^{1/2}$ |
| $A = \dfrac{{ {\dfrac{1}{{R_2 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(D_{y{\rm{D}}} - b_{\rm{D}} )} } \right]}} + \dfrac{1}{{R_1 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(b_{\rm{D}} - D_{y{\rm{D}}} )} } \right]}}} }}{{\left\{ {\dfrac{1}{{R_2 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(D_{y{\rm{D}}} - b_{\rm{D}} )} } \right]}} + \dfrac{1}{{R_1 \left[{1 - {\rm{e}}^{(R_2 - R_1 )(b_{\rm{D}} - D_{y{\rm{D}}} )} } \right]}}} \right\} - \dfrac{{2S_{\rm{f}} }}{\pi }}}$ |
| $R_1 = \sqrt {(s - B)}$ |
| $R_2 = - \sqrt {(s - B)}$ |
| $B = {\dfrac{{s\sqrt s \left[{{\rm{e}}^{ - 2\sqrt s (D_{x{\rm{D}}} - 1)} - 1} \right]}}{{{\rm{e}}^{ - 2\sqrt s (D_{x{\rm{D}}} - 1)} + 1}}}$ |
根据所求得Laplace 空间解,利用Stehfest 方法进行了数值反演[19],并以此为基础作出对应的压力、压力导数样版曲线。
图 3 为传统的压裂井三线性流矩形对称封闭边界模型与低渗透压裂井非对称区域三线性渗流模型的对比曲线,其中新模型的无因次启动压力梯度$M_{\rm{D}}$=0.01。从图中可看出,传统模型考虑的矩形对称封闭边界情形与新模型考虑的非对称边界情形的曲线存在明显的差异。图中矩形不对称边界情形的曲线由于无因次边界距离$D_{\rm{2D}}$和$D_{\rm{4D}}$($D_{\rm{2D}}$=55,$D_{\rm{4D}}$=45)远大于$D_{\rm{1D}}$ 和$D_{\rm{3D}}$($D_{\rm{1D}}$=3,$D_{\rm{3D}}$=5),可以明显看出压力及压力导数曲线先反映出直角断层的影响,然后再进入矩形封闭的反映段。由于受启动压力梯度的影响, ②~④的压力及压力导数曲线在后期也发生了上翘,可以看出,直角断层边界和无穷大边界影响的曲线两者在后期互相平行,类似于不考虑启动压力梯度影响的情形。
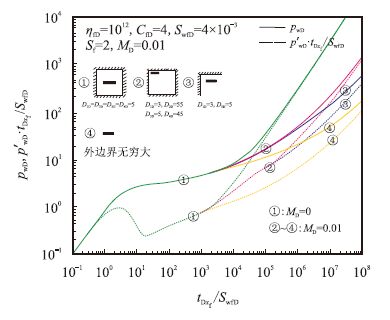 |
| 图3 矩形对称封闭边界与不对称封闭边界对比曲线 Fig. 3 Contrasting diagram of the rectangular symmetric impermeable boundary to asymmetric boundary |
图 4为平行于裂缝方向和垂直于裂缝方向两个方向上存在不同不渗透边界(一条不渗透边界和平行不渗透边界)影响的对比曲线,其中无因次启动压力梯度$M_{\rm{D}}$=0.01,4个方向上距不渗透边界的无因次距离均为5(若某一边为无穷大边界,则该边无因次边界距离为无穷大)。由图可知,不渗透边界数越多,则压力及压力导数曲线上翘幅度越大,对于一条不渗透边界和平行不渗透边界情形,压力及压力导数在垂直于裂缝方向上的边界反映时间明显早于平行于裂缝时的情形,并且在过渡阶段两者的形态也不一样,这是因为在两个方向上的渗流方式存在差异,并且无因次距离$D_{\rm{3D}}$ 和$D_{\rm{4D}}$ 是基于边界到井筒的距离定义的,而$D_{\rm{1D}}$ 和$D_{\rm{2D}}$ 则是直接基于边界到裂缝的距离定义的,存在裂缝长度的影响。两个方向上的曲线最终分别汇聚在一起,并且由于启动压力梯度的影响,在后期发生上翘。
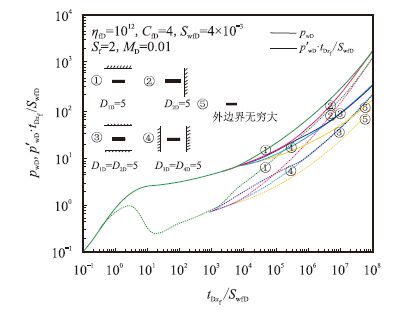 |
| 图4 两个方向上不同不渗透边界影响对比曲线 Fig. 4 Contrasting diagram of different impermeable boundary on both directions |
图 5 和图 6分别为在平行于裂缝方向上一条不渗透边界情形随断层距离($D_{\rm{1D}}$=1、3、6) 影响和受不同无因次启动压力梯度($M_{\rm{D}}$=0.01,0.005,0.001,0)影响的曲线,由图 5可知,压力波探测到不渗透边界后,相对于无穷大边界情形,压力及压力导数曲线发生上翘,并且最终形成平行于无穷大情形的曲线。距离不渗透边界越近,越早发生上翘,并在后期汇聚在一起。由图 6可知,启动压力梯度越大,压力及其导数曲线位置越高,并且上翘位置也越早。
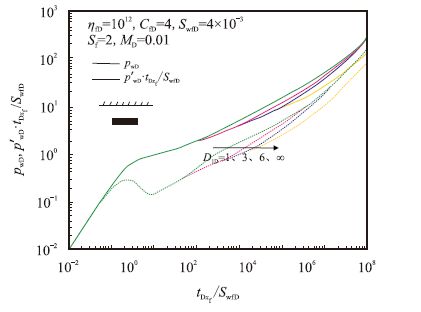 |
| 图5 受到不渗透边界距离影响的样版曲线 Fig. 5 Type curves of well test affected by the distance to impermeable boundary |
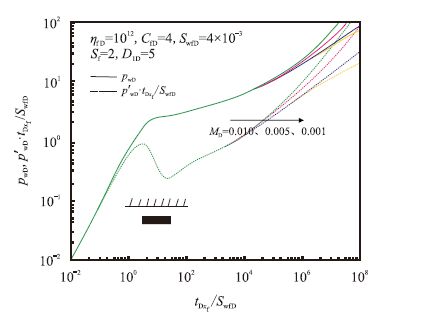 |
| 图6 受启动压力梯度影响的样版曲线 Fig. 6 Type curves of well test affected by the threshold pressure gradient |
(1) 获得了低渗透压裂井非对称区域三线性渗流模型,以及受启动压力梯度、非对称边界类型(无穷大和封闭)和边界距离影响的新型样版曲线,与常规模型样版曲线明显不同。
(2) 启动压力梯度对低渗透压裂井的试井曲线有较大影响,表现为:无因次压力及其导数曲线后期呈上升趋势;启动压力梯度越大,曲线上升时间越早、上升位置越高。
(3) 不同类型的非对称边界与不同的边界距离对试井曲线的影响类似于常规直井情形:不渗透边界条数越多,曲线上翘幅度越大;边界距离压裂裂缝越近,曲线上翘越早。
(4) 由于渗流方式和裂缝长度的影响,相同情况下(边界类型和无因次边界距离相同)不同位置(垂直或平行)的边界反映在曲线上存在明显的差异。
符 号 说 明p— 地层压力,MPa;
$p_j(j=1,2,3,4)$— 1 区、2 区、3 区、4区的地层压力,MPa;
$p_{j'}(j=1,2,3,4)$— 1′ 区、2′ 区、3′ 区、4′ 区的地层压力,MPa;
$p_{{\rm{f}}_j }(j=1,2)$— 1 区、2区裂缝压力,MPa;
$p_{\rm{w}}$— 井底压力,MPa;
$\bar p_{{\rm{wD}}}$— 拉氏空间中的无因次井底压力;
$p_{\rm{i}}$— 原始地层压力,MPa;
t— 时间,h;
$X_{\rm{f}}$— 裂缝半长,m;
$b_{\rm{f}}$— 裂缝宽度,m;
$\phi$— 地层岩石孔隙度,无因次;
$\phi_{\rm{f}}$— 裂缝岩石孔隙度,无因次;
$C_{\rm{t}}$— 储层的总压缩系数,1/MPa;
$C_{\rm{ft}}$— 裂缝岩石等温压缩系数,1/MPa;
$C_\rho$— 液体等温压缩系数,1/MPa;
$\mu$— 原油黏度,mPa$\cdot$s;
B— 原油体积系数,无因次;
K— 地层渗透率,mD;
$K_{\rm{f}}$— 裂缝渗透率,mD;
q— 井产量,m3/d;
$\lambda_{\rm{B}}$— 启动压力梯度,MPa/m;
$C_{\rm{w}}$— 井筒储集系数,m3/MPa;
$S_{\rm{f}}$— 裂缝表皮系数,无因次;
x,y— x 方向、y 方向上的距离,m;
$D_j(j=1,2,3,4)$— 到1 边界、2边界、3 边界、4边界的距离,m;
$D_x$,$D_y$— 到x 方向、y 方向上边界的边界距离,m;
s— 拉氏变量;
h— 裂缝高度,m;
下标
D— 无因次量。
| [1] | CINCO L H, SAMANIEGO V F, DOMINGUEZ A N. Transient pressure behavior for a well with a finiteconductivity vertical fracture[C]. SPE 6014, 1978. |
| [2] | CINCO L H, SAMANIEGO V F. Transient pressure analysis for fractured wells[C]. SPE 7490, 1981. |
| [3] | ECONOMIDES M J. Observations and recommendations in the evaluation of tests of hydraulically fractured wells[C]. SPE 16396, 1987. |
| [4] | LEE Shengtai,BROCKENBROUGH J R. A new approximate analytic solution for finite-conductivity vertical fractures[C]. SPE 12013, 1986. |
| [5] | OLAREWAJU J S, LEE W J. A new analytical model of finite-conductivity hydraulic fracture in a finite reservoir[C]. SPE 19093, 1989. |
| [6] | AZARI M,WOODEN W O,COBLE L E. A complete set of laplace transforms for finite-conductivity vertical fractures under bilinear and trilinear flows[C]. SPE 20556, 1990. |
| [7] | RILEY M F, BRIGHAM W E, HORNE R N. Analytic solution for elliptical finite-conductivity fractures[C]. SPE 22656, 1991. |
| [8] | LIU Yuewu,LIU Ciqun. New analysis method for the vertical fracture well[C]. SPE 30005, 1995. |
| [9] | 冯文光, 葛家理. 单一介质、双重介质中非定常非达西低速渗流问题[J]. 石油勘探与开发, 1985, 12 (1) : 56 –62. |
| [10] |
阎庆来, 何秋轩, 尉立岗, 等. 低渗透油层中单相液体渗流特征的实验研究[J].
西安石油学院学报, 1990, 5 (2) : 1 –6.
YAN Qinglai, HE Qiuxuan, WEI Ligang, et al. A laboratory study on percolation characteristics of single phase flow in lowpermeability reserviors[J]. Journal of Xi'an Petroleum Institute, 1990, 5 (2) : 1 –6. |
| [11] | YAO Yuedong, GE Jiali. Characteristics of non-Darcy flow in lowpermeability reservoirs[J]. Petroleum Science, 2011, 8 (1) : 55 –62. DOI:10.1007/s12182-011-0115-3 |
| [12] | 宋付权, 刘慈群. 低渗透油藏中垂直裂缝井的不定常渗流[J]. 试采技术, 2000, 21 (3) : 6 –8. |
| [13] |
严涛, 贾永禄. 低速非达西流有限导流垂直裂缝模型[J].
天然气工业, 2005, 25 (2) : 130 –132.
YAN Tao, JIA Yonglu. Vertical fracture model of low nonDarcy flow with finite conductivity[J]. Natural Gas Industry, 2005, 25 (2) : 130 –132. |
| [14] |
蔡明金, 贾永禄, 王永恒, 等. 低渗透双重介质油藏垂直裂缝井压力动态分析[J].
石油学报, 2008, 29 (5) : 723 –726.
CAI Mingjin, JIA Yonglu, WANG Yongheng, et al. Dynamic pressure analysis on wells with vertical fractures in low-permeability dual-porosity reservoir[J]. Acta Petrolei Sinica, 2008, 29 (5) : 723 –726. |
| [15] |
姜瑞忠, 杨明, 王公昌, 等. 低渗透油藏压裂井生产动态分析[J].
特种油气藏, 2013, 20 (1) : 52 –55.
JIANG Ruizhong, YANG Ming, WANG Gongchang, et al. Production performance analyses of low permeability fractured reservoirs[J]. Special Oil and Gas Reservoirs, 2013, 20 (1) : 52 –55. |
| [16] | 刘曰武, 肖陆锦, 赵明跃. 利用改进的试井分析方法确定压裂井到断层的距离[J]. 油气井测试, 1995, 4 (3) : 32 –35. |
| [17] |
王怒涛, 黄炳光, 邓长明. 确定压裂井到断层距离方法研究[J].
西南石油学院学报, 2001, 23 (4) : 33 –35.
WANG Nutao, HUANG Bingguang, DENG Changming. A novel method of determining the distance from fractured well to fault[J]. Journal of Southwest Petroleum Institute, 2001, 23 (4) : 33 –35. |
| [18] | 廖新维, 沈平平. 现代试井分析[M]. 北京: 石油工业出版社, 2002 . |
| [19] |
贾永禄, 赵必荣. 拉普拉斯变换及数值反演在试井分析中的应用[J].
天然气工业, 1992, 12 (1) : 60 –64.
JIA Yonglu, ZHAO Birong. Application of laplace transformation and numerical inversion to well test analysis[J]. Natural Gas Industry, 1992, 12 (1) : 60 –64. |
 2016, Vol. 38
2016, Vol. 38


