2. 中国石油大学石油工程学院, 北京 昌平 102249
2. College of Petroleum Engineering, China University of Petroleum, Changping, Beijing 102249, China
王德民、夏惠芬等[1-7] 开展了天然岩芯、人工岩 芯和刻蚀的二维玻璃岩芯室内聚合物驱油实验,认识 到多数聚合物溶液不仅具有较高的黏度,可以改善宏 观波及体积,还具有显著的弹性,能够提高各类残余 油的微观驱油效率,弹性作用对驱油效率的贡献率达 到40%。岩芯驱替过程中表现出弹性效应的这些聚 合物统称作黏弹性聚合物,其在多孔介质中的渗流规 律还需进一步认识[8-11]。与此同时,依赖于相关渗流 理论的试井分析工作需要重新评价。当前聚合物驱 油藏试井分析未考虑弹性的影响[12-18],不能真实反 映聚合物溶液在地层中流动的压力响应特征,其对试 井曲线形态的影响有待探讨。
本文通过实验测定了不同浓度下高分子聚丙烯 酰胺溶液在流变仪和多孔介质中的流变规律,以此 为基础,笔者采用基于变截面孔喉模型建立的黏弹 性本构方程表征聚合物溶液有效黏度,建立了黏弹 性聚合物驱油藏不稳定渗流数学模型,利用有限差 分方法求得数值解,研制出了相应的无因次试井图 版,并分析了弹性对试井曲线形态的影响。
1 聚合物溶液非牛顿渗流规律实验 1.1 聚合物溶液在岩芯中的渗流实验 1.1.1 实验药品本实验采用大庆油田生产的高分子量聚丙烯酰 胺(HPAM) ,其各项物化性质见表 1。
| 表1 验用聚合物物化性质 Table 1 and chemical properties of polymer in the experiment |
配制聚合物溶液采用的是大庆油田高台子地层 标准盐水,其矿化度为918 mg/L,其中各组分含量 见表 2。天然岩芯取自大庆油田高台子地层。
| 表2 标准盐水各组分含量 Table 2 Components and Concentration |
驱替实验装置如图 1 所示。主要包括驱替系 统(平流泵1 台、中间容器2 套和高压管线) 、环压系 统(手摇泵和岩芯夹持器) 、计量及测压系统(量筒、 秒表、压力表等) 。
 |
| 图1 聚合物溶液渗流实验装置简图 Fig. 1 Flow chart of polymer solution through porous media |
(1) 将岩芯抽空并饱和地层水,测量饱和水的 体积,计算岩芯的孔隙度。
(2) 用压力传感器监测岩芯两端压差,测定岩 芯的水测渗透率。
(3) 计算设定流速和水测渗透率下的压差 Δp1。
(4) 以某一流速向岩芯注入聚合物溶液,当压 力稳定时记录岩芯两端压差Δp2,计算阻力系数 Δp2/Δp1。
(5) 以相同的流速向岩芯中注入地层水,当压 力稳定时记录岩芯两端压差Δp3,计算残余阻力系 数Δp3/Δp1。
(6) 由低到高改变流速,重复步骤3、4、5、6,求 取不同流速时阻力系数、残余阻力系数。以上各个 驱替过程中,总注入量均超过5 倍的孔隙体积,以 达到稳定驱替状态。
1.1.4 实验方案设计用模拟地层水配制聚合物浓度为1 500 mg/L 的溶液,测定流速分别为0.1,0.2,0.3,0.5,1.0,2.0, 3.0,5.0 mL/min 时的阻力系数和残余阻力系数。
1.1.5 实验结果与分析采用文献[19]中公式计算有效黏度和剪切速 率,并绘制出有效黏度随剪切速率变化曲线。
如图 2 所示,随着剪切速率的增加,聚合物溶 液有效黏度先减小后增大,表现出剪切变稀和剪切 增稠的双重特性,证实本实验所用的高分子聚丙烯 酰胺属于黏弹性聚合物。
 |
| 图2 聚合物溶液在多孔介质渗流时的流变曲线 Fig. 2 Rheological curve of polymer solution through porous media |
本实验采用与实验1 完全相同的聚合物和地 层水。
1.2.2 实验仪器设备德国HAAKE 公司的RV20 旋转黏度计,用于测 量聚合物溶液的流变性。电子天平,精度为0.001 g, 用于化学试剂的定量测量。磁力搅拌器、电动搅拌 器:用于聚合物溶液的配制。
1.2.3 实验步骤由于流变性研究中所用的溶液体积较小,为了 取得准确的测量数据,避免容积法配制溶液时由于 温度变化引起的误差,溶液的配制采用称重法。
具体操作步骤如下:(1) 配好所需的地层水, 用电子天平称取一定量的聚合物。(2) 用磁力搅 拌器将烧杯中的溶剂搅起打成漩涡状,把称好的 聚合物在1 min 内均匀分散在充分搅起的漩涡中, 投放位置应在漩涡中心到器壁的2/3 处。(3) 将转 速降至80~100 r/min,避免因过高转速造成的聚合物降解。
1.2.4 实验方案用模拟地层水配制聚合物溶液,地层水矿化 度为918 mg/L 保持不变,聚合物浓度依次为800, 1 200,1 500,1 800,2 000,2 200,2 500 mg/L,旋转黏 度计设定剪切速率依次为:0.5,1.0,2.0,5.0,10.0, 20.0,50.0,100.0,200.0,500.0 s−1,测定各剪切速率 下聚合物溶液的黏度。
1.2.5 实验结果与分析原始流变曲线如图 3 所示,实验中未出现第一 牛顿区,这是由于RV20 旋转黏度计的精度不高, 不能精确测量剪切速率小于0.1 s−1 时的黏度所致; 而在剪切速率大于100 s−1 时,没有出现第二牛顿 区,却出现了剪切增稠的趋势,这是因为远在剪切 速率达到极限剪切速率之前,体系就已出现不稳 定流动和黏性发热现象,造成实验结果不可信,视 为无效数据。
 |
| 图3 同聚合物溶液浓度下的流变曲线 Fig. 3 Rheological curve of solution under different polymer concentration |
如图 4 所示,筛选实验有效数据并进行线性回 归(拟合参数见表 3) ,发现聚合物溶液表观黏度与 剪切速率在双对数图上呈现很好的线性关系,证实矿场常用浓度范围(800~2 500 mg/L) 下聚合物溶液 在中等剪切速率范围内(0.1~100.0 s−1) 符合非牛顿 幂律模式$\mu =H{{\dot{\gamma }}^{n-1}}$(μ-表观黏度,mPa·s;H-稠 度系数,mPa·sn) 。
 |
| 图4 同聚合物浓度下流变数据回归分析图 Fig. 4 Regression of rheological data under different rpolymer concentration |
| 表3 度时拟合参数表 Table 3 Fitting parameters of regression under different polymer concentration |
均质、等厚、各向同性、定压边界油藏;平面径 向流动,并符合广义达西定律;流体压缩系数很小 且为常数;忽略重力效应;聚合物溶液在渗流过程 中的剪切黏度服从幂律模式,弹性黏度用变截面孔 喉模型的弹性大小w 表征[20];考虑井筒储集与表皮 效应的影响。
2.2 有效黏度聚合物溶液在多孔介质中流动时,存在剪切流 动与弹性拉伸,前者表现为剪切黏度μv,后者表现 为弹性黏度μe,有效黏度μeff 为二者之和,综合考 虑多孔介质结构(简化为变截面孔喉模型) 和聚合物 溶液性质建立的黏弹性本构方程[20] 为
| ${{\mu }_{\text{eff}}}={{\mu }_{\text{v}}}+{{\mu }_{\text{e}}}=\left( 1+w \right){{\mu }_{\text{v}}}$ | (1) |
式中:μv-剪切黏度,mPa·s;
μe-弹性黏度,mPa·s
w-弹性黏度与黏性黏度之比,
$\omega =\frac{\frac{12n}{3n+1}\dot{\gamma }{{\theta }_{\text{f}}}\left( 1-\frac{1}{\lambda _{1}^{6}} \right)-\frac{{{\left( {{E}^{4}}-1 \right)}^{1/2}}}{\left( 1+\beta \right){\alpha }'}\left( 1-\frac{1}{\lambda _{3}^{3}} \right)}{\frac{1}{\alpha }\left( 1-\frac{1}{\lambda _{1}^{3}} \right)+6\xi +\frac{1}{{{\alpha }'}}\left( 1-\frac{1}{\lambda _{3}^{3}} \right)}$
μeff-有效黏度,mPa·s;
n-幂律指数;
${\dot{\gamma }}$-剪切速率,s−1;
θf 特征时间,s;
λ1-进入孔喉阶段孔喉比;
λ3-挤出孔喉阶段孔喉比;
ξ-孔隙因子;
α-收敛系数;
${{\alpha }'}$-扩散系数;
E-胀大比;
β-待定系数。
2.3 渗流数学模型根据连续性方程和状态方程推导出渗流控制方程
| $\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{K}{{{\mu }_{\text{eff}}}}\frac{\partial p}{\partial r} \right)=\phi {{C}_{\text{t}}}\frac{\partial p}{\partial t}$ | (2) |
初始条件
| $p\left( r,0 \right)={{p}_{\text{i}}}$ | (3) |
内边界条件
井储条件
| ${{\left. q=\frac{C}{B}\frac{\text{d}{{\text{p}}_{\text{wf}}}}{\text{d}t}-\frac{2\pi hK}{{{\mu }_{\text{eff}}}}\left( r\frac{\partial p}{\partial r} \right) \right|}_{r={{r}_{\text{w}}}}}$ | (4) |
表皮条件
| ${{\left. {{\text{p}}_{\text{wf}}}=p\left( {{r}_{\text{w}}},t \right)-S\cdot \left( r\frac{\partial p}{\partial r} \right) \right|}_{r={{r}_{\text{w}}}}}$ | (5) |
定产条件
| ${{\left. -\frac{K}{{{\mu }_{\text{eff}}}}\frac{\partial p}{\partial r} \right|}_{r={{r}_{\text{w}}}}}=\frac{q}{2\pi {{r}_{w}}h}$ | (6) |
外边界条件
定压边界
| $p\left( {{r}_{\text{e}}},t \right)={{p}_{\text{i}}}$ | (7) |
式中:p-t 时刻距井筒径向距离为r 对应的地层压 力,×10−1 MPa;
pi-原始地层压力,×10−1 MPa;
pwf-井底流压,×10−1 MPa;
t-时间,s;
Ct-综合压缩系数,(×10−1 MPa) −1;
r-径向距离,cm;
rw-井半径,cm;
re-外边界距离,cm
h-有效厚度,cm;
K-渗透率,mD;
ϕ-孔隙度,无因次;
q-流量,cm3/s;
C-井筒储集系数,cm3/(×10−1 MPa) ;
B-体积系数,无因次;
S-表皮系数,无因次。
2.4 模型的差分求解由于在一维径向流的情况下,地层压力呈漏 斗状,因而采用了不均匀的对数网格。引入变换:$x=\ln \frac{r}{{{r}_{\text{w}}}}$,并对方程在空间上采用中心差分格式、在 时间上采用向后差分格式,得到相应的差分方程
渗流方程
| ${{a}_{i}}p_{i-1}^{n+1}+{{b}_{i}}p_{i}^{n+1}+{{c}_{i}}p_{i+1}^{n+1}={{d}_{i}}\left( i=1,2,3,\cdots ,N-1 \right)$ | (8) |
其中$\begin{align} & {{a}_{i}}={{T}_{i-\frac{1}{2}}} \\ & {{b}_{i}}=-{{T}_{i+\frac{1}{2}}}+{{T}_{i-\frac{1}{2}}}+r_{i}^{2}\phi {{C}_{\text{t}}}\frac{\Delta {{x}_{i}}}{\Delta t} \\ & {{c}_{i}}={{T}_{i+\frac{1}{2}}} \\ & {{d}_{i}}=-r_{i}^{2}\phi {{C}_{\text{t}}}\frac{\Delta {{x}_{i}}}{\Delta t}p_{i}^{n} \\ \end{align}$
联立井储与表皮方程差分得到
| ${{a}_{0}}p_{0}^{n+1}+{{b}_{0}}p_{1}^{n+1}={{d}_{0}}$ | (9) |
其中
$\begin{align} & {{a}_{0}}=-\frac{B}{C}\frac{2\pi hK}{{{\mu }_{\text{eff}}}}\Delta t-\Delta x-S \\ & {{b}_{0}}=\frac{B}{C}\frac{2\pi hK}{{{\mu }_{\text{eff}}}}\Delta t+S \\ & {{d}_{0}}=S\left( p_{1}^{n}-p_{0}^{n} \right)-\Delta xp_{0}^{n}-\frac{qB}{C}\Delta x\Delta t \\ \end{align}$
对于无限大或定压边界
| ${{a}_{N-1}}p_{N-2}^{j+1}+{{b}_{N-1}}p_{N-1}^{j+1}={{d}_{N-1}}$ | (10) |
其中
${{d}_{N-1}}={{{{d}'}}_{N-1}}-{{c}_{N-1}}{{p}_{\text{e}}}$
上述差分方程(8) ~(10) 形成如下三对角矩阵 方程组,由于该方程组是非线性的,因此采用追赶 法迭代求解。求解过程为:选定时间步长,将前一 时刻的值代入,求得后一时刻的解,循环迭代,求取 不同位置处的地层压力值(近井区地层压力分布) 和 不同时刻的井底压力值(类似于开井压降数据) 。
$\left[ \begin{matrix} {{a}_{0}} & {{b}_{0}} & & & & \\ {{a}_{1}} & {{b}_{1}} & {{c}_{1}} & & & \\ & {{a}_{2}} & {{b}_{2}} & {{c}_{2}} & & \\ & & \cdots & \cdots & \cdots & \\ & & & {{a}_{N-2}} & {{b}_{N-2}} & {{c}_{N-2}} \\ & & & & {{a}_{N-1}} & {{b}_{N-1}} \\ \end{matrix} \right]\left[ \begin{matrix} {{p}_{\text{wf}}} \\ {{p}_{1}} \\ {{p}_{2}} \\ \cdots \\ {{p}_{N-2}} \\ {{p}_{N-1}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{d}_{0}} \\ {{d}_{1}} \\ {{d}_{2}} \\ \cdots \\ {{d}_{N-2}} \\ {{d}_{N-1}} \\ \end{matrix} \right]$
2.5 试井变量的无因次化方法为了分析不同因素对试井曲线形态的影响,需 要求取无因次试井模型的一般解,引入以下无因次量定义
| $\left\{ \begin{align} & {{p}_{\text{D}}}\text{=}\frac{2\pi Kh}{qB{{\mu }_{\text{eff}}}}\left( p-{{p}_{\text{i}}} \right) \\ & {{t}_{\text{D}}}=\frac{{{K}_{t}}}{n\cdot \phi {{\mu }_{\text{eff}}}{{C}_{t}}r_{\text{w}}^{2}} \\ & {{C}_{\text{D}}}=\frac{C}{n\cdot 2\pi h{{C}_{\text{t}}}r_{\text{w}}^{2}} \\ & {{r}_{\text{D}}}=\frac{r}{{{r}_{\text{w}}}} \\ \end{align} \right.$ | (11) |
选取大庆油田某聚合物驱区块一口注聚井 测试资料。其井筒半径rw 为0.1 m,油层厚度h 为3.3 m,孔隙度ϕ 为0.24,综合压缩系数Ct 为 3.864×10−4 MPa−1,体积系数B 为1.12,测试前平 均地层压力p 为10.2 MPa,关井前流动时间t 为 72.25 h,注聚速度q 为20 m3/d。室内聚合物溶液 与岩芯分析实验确定了与弹性有关的参数:特征 时间θf 为0.5 s,孔隙因子ξ 为0.125,孔喉比λ 为 8,胀大比E 为1.2,待定系数β 为1.4。
3.1 非牛顿幂律试井模型解释分析观察实测试井曲线特征,选用不考虑弹性因素 的无限大边界试井模型进行解释求参,令w = 0, re=1 000。调整幂律指数生成试井曲线图版,并对 实测压力及导数曲线进行拟合,从而进一步求取其 他解释参数。经多次尝试,实现如图 5 所示的较好 拟合效果,并求取了多个解释参数:井筒储集系数 C 为0.04 m3/MPa,表皮系数S 为−2.6,幂律指数n 为0.68,渗透率K 为0.058 6 mD。
 |
| 图5 不考虑弹性影响的非牛顿幂律流试井模型拟合图 Fig. 5 Comparison of dimensionless practical and theoretical well test curve without consideration of elasticity |
设定定压边界距离re 为100 m,注聚时间t为100 d,依据基础数据和试井解释参数计算“幂 律”、“弹性+ 幂律”两种模式下不同径向距离处的 地层压力,并绘制相应的地层压力分布曲线,如图 6 所示。考虑弹性影响后地层压力整体上升,特别是 井底压力上升幅度最大,说明聚合物溶液的弹性作 用主要影响近井地带,是造成注入压力升高的原因 之一,并会直接影响试井测压过程。
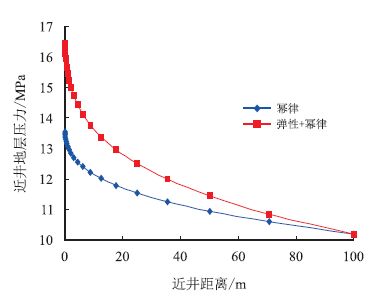 |
| 图6 “弹性”的存在对注聚井周围地层压力分布影响 Fig. 6 Effect of the existence of elasticity formation pressure distribution around polymer injection well |
依据已知参数和试井解释参数,绘制考虑弹性 因素的试井图版,并与实测试井曲线作拟合,如图 7所示。对比图 5、图 7,发现两类试井理论图版均 与实测试井曲线的拟合效果较好、拟合图相似,表 明弹性作用虽然增大了注入压力,但几乎不改变试 井曲线形态。因此,在黏弹性聚合物驱油藏的试井 分析中,可以忽略弹性的影响,采用基于非牛顿幂 律流体建立的试井模型进行有效解释,获取幂律指 数、井筒储集系数、表皮系数、渗透率、平均压力等 流体、井筒和地层参数。
 |
| 图7 考虑弹性影响的非牛顿幂律试井模型拟合图 Fig. 7 Comparison of dimensionless practical and theoretical well test curve with consideration of elasticity |
(1) 实验测定了矿场常用浓度范 围(800~2 500 mg/L) 下高分子聚丙烯酰胺聚合物 溶液在岩芯和流变仪中的流变性,证实了其在多孔 介质中渗流时存在“弹性”,且在中等剪切速率范围 内(0.1~100.0 s−1) 符合非牛顿幂律渗流模式。
(2) 在实验认识的基础上,利用基于变截面孔 喉模型建立的黏弹性本构方程表征聚合物溶液有效 黏度,建立了黏弹性聚合物驱油藏不稳定渗流数学 模型,用有限差分方法求得了数值解,并研制了无 因次试井曲线图版。
(3) 利用非牛顿幂律试井模型求取的解释参 数,重新计算并绘制了考虑弹性因素的理论试井曲 线图版,与实测压力及导数曲线合成拟合图,仍然 实现了较好拟合,且与不考虑弹性因素的非牛顿幂 律试井模型拟合效果相近,表明弹性作用虽然会大 幅增加注入压力,但几乎不改变试井曲线形态。因 而,在黏弹性聚合物驱油藏的试井分析中,可以忽 略弹性的影响,利用基于非牛顿幂律流体建立的试 井模型进行解释求参。
| [1] | WANG Demin, CHENG Jiecheng, YANG Qingyan, et al. Viscous-elastic polymer can increase microscale displacement efficiency in cores[C]. SPE 63227, 2000. |
| [2] | WANG Demin,XIA Huifen,LIU Zhongchun,et al. Study of the mechanism of polymer solution with viscoelastic behavior increasing microscopic oil displacement efficiency and the forming of steady "oil thread" flow channels[C]. SPE 68723, 2001. |
| [3] | WANG Demin, CHENG Jiecheng, WU Junzheng, et al. Experiences learned after production of more than 300 million barrels of oil by polymer flooding in Daqing oil field[C]. SPE 77693, 2002. |
| [4] | XIA Huifen, WANG Demin, WU Junzheng, et al. Elasticity of HPAM solutions increases displacement efficiency under mixed wettability conditions[C]. SPE 88456, 2004. |
| [5] | XIA Huifen,JU Ye,KONG Fanshun,et al. Effect of elastic behavior of HPAM solutions on displacement efficiency under mixed wettability conditions[C]. SPE 90234, 2004. |
| [6] |
杨树人, 王德民, 夏惠芬, 等. 黏弹性流体驱替微孔道中残余油滴的水动力学机制[J].
中国石油大学学报(自然科学版), 2011, 35 (5) : 139 –142.
YANG Shuren, WANGD Demin, XIA Huifen, et al. Hydrodynamics mechanism of visocelastic fluids displacing residual oil droplets in micro pores[J]. Journal of China University of Petroleum, 2011, 35 (5) : 139 –142. |
| [7] |
夏惠芬, 王德民, 张九然, 等. 聚合物溶液的弹性对驱油效率贡献的定量描述[J].
中国石油大学学报(自然科学版), 2012, 36 (4) : 166 –171.
XIA Huifen, WANG Demin, ZHANG Jiuran, et al. Quantitative description of contribution of elasticity of polymer solution to oil displacement efficiency[J]. Journal of China University of Petroleum, 2012, 36 (4) : 166 –171. |
| [8] | SERIGHT R S, FAN Tianguang, WAVRIK K E, et al. New insights into polymer rheology in porous media[C]. SPE 129200, 2010. |
| [9] |
曹宝格, 罗平亚. 缔合聚合物溶液在多孔介质中的流变性实验[J].
石油学报, 2011, 32 (4) : 652 –657.
CAO Baoge, LUO Pingya. An experimental study on rheological properties of the associating polymer solution in porous medium[J]. Acta Petrolei Sinca, 2011, 32 (4) : 652 –657. |
| [10] | YIN Hongjun, WANG Demin, ZHONG Huiying, et al. Flow characteristics of viscoelastic polymer solution in micro-pores[C]. SPE 154640, 2012. |
| [11] | WILTON R R,TORABI F. Rheological assessment of the elasticity of polymers for enhanced heavy oil recovery[C]. SPE 165488, 2013. |
| [12] | IKOKU C U, RAMEY H J Jr. Transient flow of nonNewtonian power-law fluids in porous media[C]. SPE 7139, 1979. |
| [13] | VONGVUTHIPORNCHAI S, RAGHAVAN R. Well test analysis of data dominated by storage and skin:NonNewtonian power-law fluids[C]. SPE 14454, 1987. |
| [14] | 王海涛. 注聚渗流规律与试井分析研究[D]. 成都:西南石油大学, 2006. |
| [15] | LI Zhitao, DELSHAD M. Development of an analytical injectivity model for non-Newtonian polymer solutions[C]. SPE 163672, 2013. |
| [16] |
程时清, 聂向荣. 聚合物驱复合油藏试井模型与典型曲线[J].
华中科技大学学报(自然科学版), 2012, 40 (4) : 110 –113.
CHENG Shiqing, NIE Xiangrong. Well test model and type curves of composite reservoirs with polymer flooding[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2012, 40 (4) : 110 –113. |
| [17] | VAN Den Hoek P J, MAHANI H, SOROP T, et al. Application of injection fall-off analysis in polymer flooding[C]. SPE 154376, 2012. |
| [18] | ALEX R V P, HEBER C L, HECTOR P B, et al. A new general flow model for well test analysis for fluids used in enhanced oil recovery projects[C]. SPE 164886, 2013. |
| [19] | HIRASAKI G J,POPE G A. Analysis of factors influencing mobility and adsorption in the flow of polymer solutions through porous media[C]. SPE 4026, 1974. |
| [20] |
曹仁义, 程林松, 郝炳英, 等. 黏弹性聚合物溶液渗流数学模型[J].
西安石油大学学报(自然科学版), 2007, 22 (2) : 107 –109.
CAO Renyi, CHENG Linsong, HAO Bingying, et al. Mathematical model of viscous-elastic polymer solution seepage[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2007, 22 (2) : 107 –109. |
 2016, Vol. 38
2016, Vol. 38


