当前国际能源形势严峻,能源的开发利用已 成为各国关注的焦点。受美国页岩气成功开发的 影响,全球页岩气勘探开发呈快速发展态势[1-3]。 2012 年,美国天然气销售量更达到7 160×108 m3。 中国主要盆地的页岩气资源量约26.0×1012 m3,与 美国的28.3×1012 m3 大致相当,经济价值巨大[4]。 针对页岩气藏的开采,现主要采用压裂水平井的方 式[5-7],并利用Eclipse 等建模软件,对页岩气藏的 产能及动用情况等进行预测,这些数值模拟软件可 以很好地模拟地层和裂缝的复杂情况,但当网格步 长比较小的情况下,软件的运行时间会大大增加, 对于百万级的储层模型,甚至需要几个小时的计算 时间,给油藏工作者带来诸多不便。为了快速准确 地预测地层动用情况,需要找到一种更为快速有效 的办法。波前快速推进法是一种高效追踪边界运移 情况的办法,现已广泛应用在医学、地质学等方面。 利用波前快速推进法对储层的动用情况进行预测, 即使针对百万级的网格也仅需要十几分钟的时间, 大大提高了网格计算的效率。
1 波前快速推进法(FMM)简介 1.1 波前快速推进法计算过程FMM 是由Sethian J A 于1999 年提出来的一 种计算波前运移情况的方法[8],其计算过程如 图 1[9-10]。
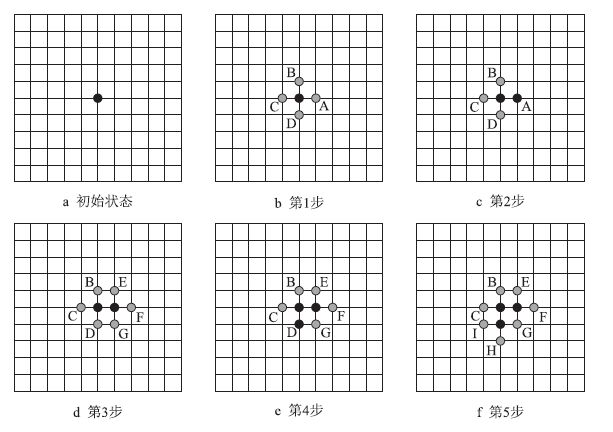 |
| 图1 波前快速推进法计算过程示意图 Fig. 1 General view of the fast marching method |
(1)把图 1a 中的确定点定义为起始点(τ = 0), 找到与起始点相连接的相邻点A、B、C、D,如图 1b;
(2)利用迎风法计算波前缘到达各相邻点的时 间,并选出最小值点,假设为A,如图 1c;
(3)将A 点设为新的起始点,并找到A 的未确 定相邻点E、F、G,如图 1d;
(4)计算波传播到E、F、G 各点的时间,并在所 有的相邻点中选择出最小值,假设为D;
(5)重复步骤(3)和步骤(4),直到所有点被标 记为确定点。
1.2 波前快速推进法计算方法对波的前缘进行预测,首先需要求得Eikonal 方程(程函方程)的解,如下式
| $F\left| \nabla T \right|=1$ | (1) |
式中:F-波前缘的移动速度,m/s;T-时间,s。
假设Ti,j 未知,Ti,j+1、Ti,j-1、Ti+1,j、Ti-1,j 都已知(图 2),Sethian 提出运用如下方法来计算Ti,j
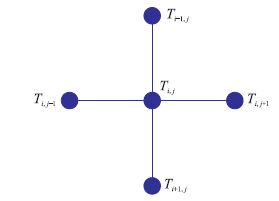 |
| 图2 波前快速推进法中的相邻点 Fig. 2 Neighbourhood point in fast marching method |
| $\begin{align} & {{\left| \nabla T \right|}^{2}}=\max {{\left( D_{i,j}^{-x}T,-D_{i,j}^{x}T,0 \right)}^{2}}+ \\ & \max {{\left( D_{i,j}^{-y}T,-D_{i,j}^{y}T,0 \right)}^{2}} \\ \end{align}$ | (2) |
由式(1)可得
| $\left| \nabla T \right|=\frac{1}{F}$ | (3) |
将式(3)代入(2)式,可以得到
| $\begin{align} & \frac{1}{{{F}^{2}}}=\max {{\left( D_{i,j}^{-x}T,-D_{i,j}^{x}T,0 \right)}^{2}}+ \\ & \max {{\left( D_{i,j}^{-y}T,-D_{i,j}^{y}T,0 \right)}^{2}} \\ \end{align}$ | (4) |
式中:$\begin{align} & D_{i,j}^{-x}T=\left( {{T}_{i,j}}-{{T}_{i-1,j}} \right)/\Delta x; \\ & D_{i,j}^{x}T=\left( {{T}_{i+1,j}}-{{T}_{i,j}} \right)/\Delta x; \\ & D_{i,j}^{-y}T=\left( {{T}_{i,j}}-{{T}_{i,j-1}} \right)/\Delta y; \\ & D_{i,j}^{y}T=\left( {{T}_{i,j+1}}-{{T}_{i,j}} \right)/\Delta y; \\ \end{align}$。
在x 方向上,比较$D_{i,j}^{-x}T,D_{i,j}^{x}T$与0 的大小,选 出最大值,假设为$D_{i,j}^{-x}T$,从而确保波沿x 方向一直 在向外推进;同理,也选出y 方向的最大值,假设为$D_{i,j}^{-y}T$,从而式(4)可以改写为
| ${{\left( \frac{{{T}_{i,j}}-{{T}_{i-1,j}}}{\Delta x} \right)}^{2}}+{{\left( \frac{{{T}_{i,j}}-{{T}_{i,j-1}}}{\Delta y} \right)}^{2}}=\frac{1}{{{F}^{2}}}$ | (5) |
这是一个简单的一元二次方程,对其求解,选 出较大的值作为方程的解,从而确定Ti,j 的值[11]。
2 程函方程构建Lee W J 于1982 年提出了调查半径的概念,并 给出了调查半径的计算公式[12]
| $r=\sqrt{\beta \alpha t}$ | (6) |
式中: r-调查半径,m;
t-压力波传播的时间,s;
α-导压系数,m2/s,且α = 10-6K/ (μϕct);
K-渗透率,mD;
μ-黏度,mPa·s;
ϕ-孔隙度,无因次;
ct-综合压缩系数,MPa-1;
β-与流态有关的系数,无因次,在不同的流动 状态下有不同的值[13],如在线性流中β = 2,在平面 径向流中β = 4,在球形径向流中β = 6。
但这种算法不适用于各向异性与水力压裂储层 的计算,尤其对于非常规储层多级压裂水平井的预测会产生较大的误差。Vasco D W 等提出了各向异 性油藏压力波前缘推进的程函方程[14]
| $\sqrt{\alpha }\left| \nabla \tau \left( {\vec{x}} \right) \right|=1$ | (7) |
式中:$\tau \left( {\vec{x}} \right)$飞行时间,s0.5,与波的传播时间有关
| $\tau =\sqrt{\beta T}$ | (8) |
Van Kruysdijk C P J W 等提出了一个多段压裂 水平井的复合线性模型[15] (图 3),这个模型将流态 分为4 个阶段:裂缝线性流、双线性流、复合线性 流、拟径向流。在模拟过程中,在不同区域分别选 取相应的值。
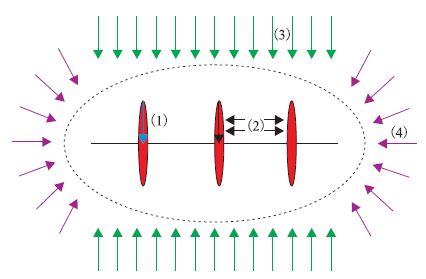 |
| 图3 复合线性流模型 Fig. 3 Compound linear flow model of the multi-stage fractured horizontal well |
考虑基质中气体存在滑脱,则表观渗透率为
| ${{K}_{\text{am}}}={{K}_{\text{m}}}\left( 1+\frac{0.0315K_{\text{m}}^{-0.6192}}{{{p}_{\text{m}}}} \right)$ | (9) |
| ${{m}_{\text{m}}}=2\int_{{{p}_{\text{i}}}}^{{{p}_{\text{m}}}}{\frac{p}{{{\mu }_{\text{g}}}Z}}\text{d}p$ | (10) |
| ${{t}_{\text{a}}}=\frac{\left( {{\mu }_{\text{g}}}{{c}_{\text{t}}} \right)}{{{q}_{\text{sc}}}\left( t \right)}\int_{0}^{\text{t}}{\frac{{{q}_{\text{sc}}}\left( \tau \right)}{\mu \left( {\bar{p}} \right){{c}_{t}}\left( {\bar{p}} \right)}\text{d}\tau }$ | (11) |
基质的综合压缩系数为
| ${{c}_{\text{tm}}}={{c}_{\text{m}}}+{{c}_{\text{g}}}+{{c}_{\text{d}}}$ | (12) |
其中,考虑吸附的压缩系数为[18]
| ${{c}_{\text{d}}}=\frac{{{p}_{\text{sc}}}\bar{Z}{{T}_{\text{r}}}p\text{L}}{{{\phi }_{\text{m}}}{{Z}_{\text{sc}}}{{T}_{\text{sc}}}\bar{p}{{\left( p\text{L+}\bar{p} \right)}^{2}}}$ | (13) |
得到基质的控制方程为
| ${{\nabla }^{2}}{{m}_{\text{m}}}=\frac{{{10}^{-6}}{{\mu }_{\text{gi}}}{{\phi }_{\text{m}}}{{c}_{\text{tim}}}}{{{K}_{\text{ami}}}}\frac{\partial {{m}_{\text{m}}}}{\partial {{t}_{\text{a}}}}$ | (14) |
因此
| ${{\alpha }_{\text{m}}}=\frac{{{10}^{-6}}{{K}_{\text{ami}}}}{{{\phi }_{\text{m}}}{{\mu }_{\text{gi}}}{{c}_{\text{tim}}}}$ | (15) |
同理,裂缝中的控制方程可以写成
| ${{\nabla }^{2}}{{m}_{\text{f}}}+\bar{q}=\frac{{{10}^{-6}}{{\mu }_{\text{gi}}}{{\phi }_{\text{f}}}{{c}_{\text{tif}}}}{{{K}_{\text{fi}}}}\frac{\partial {{m}_{\text{f}}}}{\partial {{t}_{\text{a}}}}$ | (16) |
因此
| ${{\alpha }_{\text{f}}}=\frac{{{10}^{-6}}{{K}_{\text{fi}}}}{{{\phi }_{\text{f}}}{{\mu }_{\text{gi}}}{{c}_{\text{tif}}}}$ | (17) |
其中
| ${{c}_{\text{tf}}}={{c}_{\text{g}}}+{{c}_{\text{f}}}$ | (18) |
式中:
Kam-基质的表观渗透率,mD;
Km-基质渗透率,mD;
Kami-基质的初始渗透率,mD;
Kfi-裂缝的初始渗透率,mD;
μg-气体黏度,mPa·s;
ctm-基质的综合压缩系数,MPa-1;
cm-基质的压缩系数,MPa-1;
cf -裂缝压缩系数,MPa-1;
cg-气体的压缩系数,MPa-1;
cd-解吸压缩系数,MPa-1;
pm-基质中的油藏压力,MPa;
psc-标准状态下的压力,MPa;
pi-原始地层压力,MPa;
p-平均地层压力,MPa;
ta-拟时间,s;
Zi-原始条件下的气体压缩因子,无因次;
Tr-地层温度,℃;
pL-兰氏压力,MPa;
ϕm-基质孔隙度,无因次;
ϕf-裂缝有效孔隙度,无因次;
Zsc-标准状态下的气体压缩因子,无因次;
Z-平均气体压缩因子,无因次;
Tsc-标准状态下的温度,℃;
qsc -标准状态下的产气速率,m3/s;
q-基质向裂缝的贡献,109MPa/(s·m2)。
从而分别得到考虑解吸与滑脱效应的基质及裂 缝的程函方程为
| $\sqrt{{{\alpha }_{\text{m}}}}\left| \nabla \tau \right|=1$ | (19) |
| $\sqrt{{{\alpha }_{\text{f}}}}\left| \nabla \tau \right|=1$ | (20) |
式(19)和式(20)中的$\sqrt{\alpha }$相当于式(1)中的F,τ 相当于式(1)中的T。根据式(4),可以得到基质 和裂缝中程函方程的解,由下式确定
| $\begin{align} & \frac{{{\mu }_{\text{gi}}}{{\phi }_{\text{m}}}{{c}_{\text{tim}}}}{{{10}^{-6}}{{K}_{\text{ami}}}}=\max {{\left( D_{i,j}^{-x}\tau -D_{i,j}^{x}\tau ,0 \right)}^{2}} \\ & +\max {{\left( D_{i,j}^{-y}\tau -D_{i,j}^{y}\tau ,0 \right)}^{2}} \\ \end{align}$ | (21) |
| $\begin{align} & \frac{{{\mu }_{\text{gi}}}{{\phi }_{\text{f}}}{{c}_{\text{tif}}}}{{{10}^{-6}}{{K}_{\text{fi}}}}=\max {{\left( D_{i,j}^{-x}\tau -D_{i,j}^{x}\tau ,0 \right)}^{2}} \\ & +\max {{\left( D_{i,j}^{-y}\tau -D_{i,j}^{y}\tau ,0 \right)}^{2}} \\ \end{align}$ | (22) |
由于压力波在裂缝中的传播速度比在基质中的 速度大得多,而且裂缝的宽度非常小,可以忽略压 力波在裂缝中垂直于裂缝的传播,认为压力波在裂 缝中是一维线性传播,假设水平井是沿着x 轴方向, 裂缝是沿着y 轴方向的,从而式(22)可以简化为
| $\frac{{{\mu }_{\text{gi}}}{{\phi }_{\text{f}}}{{c}_{\text{tif}}}}{{{10}^{-6}}{{K}_{\text{fi}}}}=\max {{\left( D_{i,j}^{-y}\tau -D_{i,j}^{y}\tau ,0 \right)}^{2}}$ | (23) |
构建图 4 所示的二维模型,计算过程中选取的 储层参数如表 1。图中水平井的长度L = 1 000 m, 裂缝长Lf = 800 m,裂缝间距200 m,通过波前快速 推进法来模拟计算压力波的传播,得到储层的动用 情况如图 5。
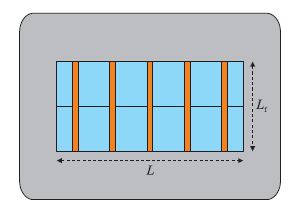 |
| 图4 页岩气多级压裂水平井示意图 Fig. 4 Model of the multi-stage fractured horizontal well in shale gas reservoir |
| 表1 储层参数表 Table 1 Parameters of the reservoir |
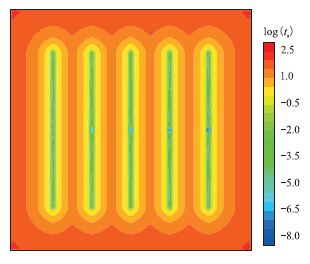 |
| 图5 储层动用情况示意图 Fig. 5 Drainage at different time |
图 5 中的等值线为时间的等值线,代表不同时间压力波传播的范围,从图中可以看到,当压力波远离裂缝时,时间等值线原来越密集,说明压力波 的传播速度越来越慢。
从图 6 动用体积与拟时间的关系曲线中可以看 出,A 点代表压力波传播到改造区边缘,在压力波 传播到SRV 边界之前,动用体积随着时间段的增长 迅速增大,当压力波传播到SRV 边界之后,动用体 积随时间增加的速度变慢。
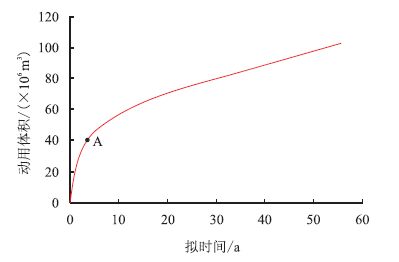 |
| 图6 动用体积与拟时间关系曲线 Fig. 6 Drainage volume at different time |
为了研究基质的解吸与滑脱效应对储层动用情 况的影响,对油藏参数做如下调整(表 2)。
| 表2 不同情况下的波前运移程函方程 Table 2 Eikonal equation under different conditions |
根据表 2,从而得到不同情况下的储层动用情 况,如图 7。图 7 中的绿色区域、红色区域和粉色区 域分别代表气藏开发3 个月、3 年和30 年压力波的 传播范围。
 |
| 图7 不同情况下的储层动用情况 Fig. 7 Drainage under different conditions |
结合图 8 动用体积与拟时间的关系曲线可以发 现,滑脱效应对储层动用的影响很大,在考虑滑脱 效应时,储层的动用体积要比不考虑滑脱效应时的 储层动用体积要大。而解吸作用对储层动用的影响 非常小,考虑基质解吸时的储层的动用程度要比不 考虑解吸时的动用程度小。
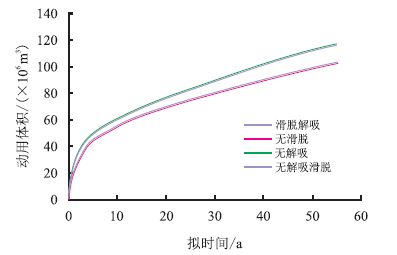 |
| 图8 解吸滑脱对储层动用的影响 Fig. 8 The influence of desorption and slippage on drainage area |
(1)分别对裂缝和基质构建不同的程函方程,根据Sethian 提出的方法对其进行运算,达到对压力 波前缘预测的目的。
(2)利用Van Kruysdijk 等提出的多段压裂水平井的复合线性模型,在不同的渗流区域考虑不同的 流态,从而使模拟结果与实际更加符合。
(3)实现了波前快速推进法对储层动用体积的直观预测,可以直接从图版上看到压力波在不同时 期所传播到的位置。
(4)从解吸及滑脱效应的对比中可以看到,滑脱效应对于动用体积的影响很大,而解吸作用对储 层动用的影响很小。
(5)滑脱效应可以加快储层的动用速度,而基 质的解吸作用降低了储层的动用速度。
| [1] |
江怀友, 宋新民, 安晓璇, 等. 世界页岩气资源勘探开发现状与展望[J].
大庆石油地质与开发, 2008, 27 (6) : 10 –14.
JIANG Huaiyou, SONG Xinmin, AN Xiaoxuan, et al. Current state and outlook of exploration and development of the shale gas resources in the world[J]. Petroleum Geology & Oilfield Development in Daqing, 2008, 27 (6) : 10 –14. |
| [2] | AMAKRISHNAN H, PEZA E A, SINHA S, et al. Understanding and predicting fayetteville shale gas production through integrated seismic-to-simulation reservoir characterization workflow[C]. SPE 147226, 2011. |
| [3] | MATTAR L. Production analysis and forecasting of shale gas reservoirs:Case history-based approach[C]. SPE 119897, 2008. |
| [4] | 孙赞东, 贾承造, 李相方. 非常规油气勘探与开发[M]. 北京: 石油工业出版社, 2011 . |
| [5] | VIVEK S. Shale gas reservoir modeling:Form nanopores to laboratory[C]. SPE 163065, 2012. |
| [6] | MEDEIROS F, KURTOGLU B, OZKAN E, et al. Analysis of production data from hydraulically fractured horizontal wells in shale reservoirs[C]. SPE 110848, 2010. |
| [7] | MYERS R R. Stimulation and production analysis of underpressured(marcellus) shale gas[C]. SPE 119901, 2008. |
| [8] | SETHIAN J A. Level set methods and fast marching methods[J]. Journal of Computing and Information Technology, 2003, 11 (1) : 1 –2. DOI:10.2498/cit.2003.01.01 |
| [9] | XIE J, YANG C, GUPTA N, et al. Integration of shale gas production data and microseismic for fracture and reservoir properties using fast marching method[C]. SPE 161357, 2012. |
| [10] | ZHANG Y, YANG C, KING M J, et al. Fast-marching methods for complex grids and anisotropic permeabilities:Application to unconventional reservoirs[C]. SPE 163637, 2013. |
| [11] | BARENTAEN J A. On the implementation of fast marching methods for 3D lattices[R]. 2001. |
| [12] | LEE W J. Well Testing[M]. Richardson: Society of Petroleum Engineers, 1982 . |
| [13] | KIM J U, DATA-GUPTA A, BROUWER R, et al. Calibration of high-resolution reservoir models using transient pressure data[C]. SPE 124834, 2009 |
| [14] | VASCO D W, KEERS H, KARASAKI K. Estimation of properties using transient pressure data:An asymptotic approach[J]. Water Research, 2000, 36 (12) : 3447 –3465. DOI:10.1029/2000WR900179 |
| [15] | VAN KRUYSDIJK C P J W, DULLAERT G M. A boundary element solution of the transient pressure response of multiple fractured horizontal wells[C]. Cambridge:The 2nd European Conference of the Mathematicsof Oil Recovery, 1989. |
| [16] |
罗瑞兰, 程林松, 朱华银, 等. 研究低渗气藏气体滑脱效应需注意的问题[J].
天然气工业, 2007, 27 (4) : 92 –94.
LUO Ruilan, CHENG Linsong, ZHU Huayin, et al. The Problems that should be paid attention to in low permeability gas reservoir gas with slippage effect[J]. Natural Gas Industry, 2007, 27 (4) : 92 –94. |
| [17] | MEDEIROS F, KURTOGLE B, OZKAN E, et al. Analysis of production data from hydraulically fractured horizontal wells in shale reservoirs[C]. SPE 110848, 2010. |
| [18] | LEWIS A M, HUGHES R G. Production data analysis of shale gas reservoir[C]. SPE 116688, 2008. |
 2016, Vol. 38
2016, Vol. 38


