2. 中国石油西南油气田蜀南气矿勘探开发研究所, 四川 泸州 646200
2. Research Institute of Exploration and Development, Shunan Gas Field, Southwest Oil and Gas Field, PetroChina, Luzhou, Sichuan 646200, China
页岩气藏目前主要采用水平井分段压裂的方式 进行开发[1],气井在生产中表现出初期产量迅速递 减,生产能力迅速减弱的特征,这种情况在异常高 压页岩气藏开发中表现得更为严重。页岩气井不限 制生产的开采方式,在异常高压页岩气藏开发中已 受到质疑。国外学者对页岩气井应力敏感的判断 等进行过一定理论研究,北美的Haynesville 气田也 开展了现场试验,初步认为异常高压页岩气藏存在 应力敏感[2-4],但是对异常高压页岩气藏应力敏感 的发生机制并未做出较为深入的研究。在低渗透 气藏的开发中,储层是否存在较强的应力敏感一直 存在争议[5],如何进行岩芯实验许多学者也做了探 讨[6-9]。笔者从理论上分析了与储层应力敏感相关 的参数及产生裂缝应力敏感的原因,认为储层岩石 与支撑剂充填的压裂缝结构上存在较大的差别,储 层岩石由于经历过成岩作用的压实,应力敏感相对 较弱,而压裂缝并未经历这一作用,当采用高压差、 高产量生产时,可能导致压裂缝中的支撑剂在高闭 合压力下发生破裂、嵌入储层、或高速气体使得支 撑剂发生移动,从而大幅度降低压裂缝的渗透率。 采用数值模拟的方法,论证了应力敏感对页岩气藏 开发的影响,同时采用图形判断法对页岩气井因为 配产不合理导致气井产能降低的情况进行了分析, 对页岩气的合理开发提供了依据。
1 储层应力敏感特征在油气田的开采过程中,地层压力下降导致有 效应力增加,从而使岩石产生变形。岩石变形使得 渗透率发生变化,这种现象被称为储层岩石的渗透 率应力敏感性。由有效应力、上覆静岩压力和地层 流体压力的关系(式1)可知[10],异常高压使得储层 岩石的原始有效应力降低,且增大了气藏开发过程 中有效应力的变化范围。
| $\bar{\sigma }=\sigma -\alpha p$ | (1) |
式中:σ-岩石基质的垂直有效应力,MPa;
σ-上覆静岩压力,MPa;
α-Biot 系数,无因次;
p-地层流体静压,MPa。
岩石的变形量一方面与有效应力大小有关,另 一方面,也和岩石物理性质有关。显然,岩石越坚 硬,变形量越小;应力敏感越弱,岩石越疏松,变形 量越大,应力敏感越强。Palmer I 等[11] 对多孔介质 应力敏感进行了推导,结果为
| $\frac{K}{{{K}_{\text{i}}}}={{\text{e}}^{-3{{C}_{\text{fu}}}\left( {{p}_{\text{i}}}-p \right)}}$ | (2) |
| ${{C}_{\text{fu}}}=\frac{\left( 1+v \right)\left( 1-2v \right)}{\left( 1-v \right){{\phi }_{\text{i}}}E}$ | (3) |
式中: K-地层渗透率,mD;
Ki-原始地层渗透率,mD;
pi-原始地层压力,MPa;
Cfu-孔隙体积压缩率,MPa−1;
E-杨氏模量,MPa;
ν-泊松比,无因次;
ϕi-原始孔隙度,%。
式(2)可简化为式(4)的形式,即通常所说的应 力敏感指数表达式
| $\frac{K}{{{K}_{\text{i}}}}\text{=}{{\text{e}}^{-\gamma \left( {{p}_{\text{i}}}-p \right)}}$ | (4) |
式中:γ-渗透率敏感指数(渗透率模量),MPa−1。
可见,应力敏感只和岩石杨氏模量、泊松比、孔 隙度以及压降有关系。因此,储层是否产生较强的 变形,从而导致具有较强的应力敏感特征,是由储 层的岩石力学性质及初始孔隙度直接决定的,岩石 初始渗透率的高低和岩石应力敏感强弱并无直接 关系。
杨氏模量越高,泊松比越低,岩石越不容易压 缩,储层渗透率变化比例越小。对于同一地层岩石 而言,物性参数一定,其渗透率敏感曲线是一个渗 透率随压力变化的方程。对于深埋地下的岩石而 言,经过成岩作用后,其孔隙体积压缩率通常较小, 因此由于孔隙压力改变导致的渗透率变化幅度一般 不大。
不同杨氏模量下渗透率随地层压力变化曲线见 图 1(原始地层压力50 MPa,初始孔隙度5%,杨氏 模量(6.9~41.4)×103 MPa,泊松比0.2)。四川龙马 溪页岩气藏泊松比在2.0 左右,初始孔隙度5% 左 右,杨氏模量在(13~16)×103 MPa,可以看出,即使 压降达到40 MPa,渗透率下降比例仅为10% 左右, 说明实际储层的应力敏感较弱。
 |
| 图1 不同杨氏模量下渗透率随地层压力变化图 Fig. 1 Permeability change with formation pressure under different Young′ s modulus |
除了储层应力敏感能导致储层渗透率降低,增 加有效应力同样会影响压裂缝的性能,有效应力增 加,压裂缝会逐渐闭合,导流能力将逐渐降低。如 图 2 展示了国外几种常用支撑剂导流能力随有效应 力增加而降低的情况[12-13]。
 |
| 图2 不同支撑剂导流能力随有效应力变化曲线 Fig. 2 Flow conductivity of different proppant varying with the effective stress |
和地层岩石不同的是,人工裂缝并不是处于一 种稳定的状态,主要表现在以下两个方面。
(1)人工压裂缝中支撑剂导流的能力随压力和 受压时间双重影响而变化。从图 3 中长期导流能力 实验可以看出[14],支撑剂导流能力随闭合应力增加 而降低。理论上说,裂缝中充填的支撑剂未经成岩 作用,其充填空间的结构非常不稳定,随着闭合压 力增大,支撑剂在岩石中的嵌入和破碎对支撑剂导 流能力的影响很大,这种结构性变形是造成裂缝应 力敏感的主要原因。特别是在塑性较强(低杨氏模 量、高泊松比)的储层,压实嵌入可能更加严重。同 时,从图 3 还可以观察到,压裂砂的导流能力和闭 合压力并非一一对应的关系,而是在相同闭合压力 下随着加压时间的增长,导流能力不断降低[15]。在 不同闭合应力下,导流能力变化的趋势并不相同。 这就预示着,以不同的压降速度生产,具有不同的 应力敏感方程。
 |
| 图3 裂缝长期导流能力随闭合压力和时间变化曲线 Fig. 3 Fracture long-term flow conductivity with the closure pressure and time |
(2)高流速气体会引起压裂砂运移。有大量的 研究表明[16],气井压裂后如果产量过高,高速气流 的冲击力会使裂缝中的支撑剂发生运移,使裂缝失 去支撑而闭合,失去高导流能力,甚至砂粒随气流 从井底流到地面过程中还会刺坏设备。压裂砂的这 种运移导致了压裂缝结构更加不稳定。因此,如果 气井产量过高,引起了支撑剂运移,那么采用不同 产量生产,裂缝渗透率的变化趋势将有所不同,裂 缝渗透率敏感方程也将不同。
综上所述,人工裂缝的应力敏感表现出与储层 应力敏感不同的特征,其应力敏感曲线方程与生产 压差和压降时间有关。
3 考虑应力敏感特征的页岩气藏数值模拟 3.1 模型的建立为研究应力敏感对生产的影响,建立了双孔数 值模型,模型大小1 300 m × 800 m × 50 m,为更好地 表述裂缝宽度,同时提高运算速度,采用不等间距 网格,x 方向网格大小为0.01(裂缝宽度)~45 m,y方 向网格为10~30 m,z 方向分为5 层,每层10 m,净 毛比0.6,模拟的网格节点为129 × 41 × 10= 52 890 个,模拟井水平段长度为1 000 m,分10 段压裂,压 裂缝半长200 m,缝高30 m,主裂缝宽度采用最小 步长0.01 m,模型中部深度2 500 m,原始地层压力50 MPa,假定气体均为CH4,采用单组分模型,模型 网格见图 4。储层参数:基质孔隙度5.0%;裂缝孔 隙度0.2%;基质渗透率1.0×10−5 mD;天然裂缝渗透 率1.0×10−4 mD;压裂缝渗透率200 mD;Langmiur 体积3 m3/t;Langmiur 压力5 MPa。
 |
| 图4 页岩气水平井分段压裂单井数模网格图 Fig. 4 Single well reservoir simulation model mesh of horizontal shale gas well with multiple hydraulic fractures |
为研究应力敏感对单井预测最终采气 量(EUR)的影响,分别比较了不考虑应力敏感、仅考 虑储层应力敏感、仅考虑裂缝应力敏感、同时考虑储 层和裂缝应力敏感下最终采收率的情况,如图 5(储 层应力敏感曲线采用图 1 中杨氏模量为6.9×103 MPa 的曲线、裂缝应力敏感采用了图 3 的平均数据)。可 以看出:仅考虑储层应力敏感,EUR将降低8.4%,仅 考虑裂缝应力敏感EUR 将降低11.1%,同时考虑储 层及压裂缝应力敏感时EUR 将降低17.0%,应力敏 感对页岩气井的EUR 造成了不利影响,压裂缝应力 敏感比储层应力敏感影响更大。由于本次模拟杨氏 模量的取值相对较低,因此,实际储层的应力敏感相 对更弱,而裂缝应力敏感影响相对更强。
 |
| 图5 应力敏感对EUR 影响 Fig. 5 The comparison of stress sensitivity impact on EUR |
根据前文分析可知,地层应力敏感曲线应当 是一个函数,而压裂缝应力敏感由于受时间影响, 可能表现为多个衰减函数。因此,首先对地层应力 敏感和压裂缝应力敏感曲线均采用固定的应力敏 感曲线进行模拟,用以确定初期配产对最终采气 量的影响。
图 6 对比了不同初期配产情况下累产情况(初 期产量分别为无阻流量QAOF 的0.4、0.6、0.8、1.0 倍),模拟时采用了相同的渗透率递减方程。可以看 出,不论以何种模式生产,配产对30 a 的最终采气量 影响很小。只有当以一个很低值生产时(0.2QAOF),会致使30 a 累产明显减少。因此可以得出如下结 论:即如果页岩气井应力敏感存在,且渗透率随压 降以一种恒定的模式变化,那么不论以何种产量生 产,对最终采气量的影响甚小,初期的产量控制显 得并不必要。
 |
| 图6 不同初期配产下累产量 Fig. 6 The comparison of cumulative gas production with different initial allocation |
但是如果考虑使气井具有较长的稳产时间, 从而保障为下游稳定地供气,仍然可以选择在初 期以较低的产量生产(如图 7,表 1)。当气井以 0.4~0.6QAOF 作为初期产量配产时,具有较长的稳 产时间,而30 a 最终采气量几乎相当。
 |
| 图7 不同初期配产下日产量 Fig. 7 The comparison of gas production rate with different initial allocation |
| 表1 不同初期配产下生产对比表 Table 1 The comparison of gas production with different initial allocation |
由于压裂缝结构的不稳定,以不同产量生产, 储层压力下降至相同水平,其变形量并不同,压裂 缝应力敏感可能表现为多个应力敏感方程。因此对 于初期高配产(0.8 倍无阻流量)方案,裂缝使用了一 个相对较高的渗透率敏感指数(0.02 MPa−1):对于 初期低配产(0.4 倍无阻流量)方案,裂缝使用了一个 相对较低的渗透率敏感指数(0.01 MPa−1)。(模拟 中仅改变了裂缝的应力敏感曲线,其他条件相同, 最低井底流压限制为2.00 MPa)。
从图 8 可以看出,初期采用较低产量配产,稳 产时间更长,虽然初期采气量比高配产方案低,但 最终EUR 值较初期高配产方案高。低配产方案日 产气量在1 100 d、累产气量在3 300 d 左右分别超 过了初期高配产方案。
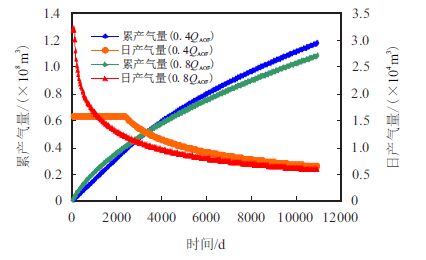 |
| 图8 考虑变裂缝应力敏感曲线不同配产下的产量 Fig. 8 The gas production considering the variable fracture stress sensitivity curves with different initial allocation |
该模拟结果佐证了压裂气井控制产量生产的有 效性,和国外的异常高压页岩气藏[4] 控制产量生产 从而提高生产效果的现场实践相吻合。
4 页岩气井开采中应力敏感判断页岩气藏开发中是否由于应力敏感影响了生产 能力,和该地区的地质条件(如是否具有低杨氏模 量、高泊松比特征)、工艺水平、开采速度均具有一 定的联系。因此现场如果需要采取限产措施,首先 要确定该气藏是否因为不合理配产影响了气井产能 的发挥。如果配产不同导致最终生产能力不同,那 么不同配产情况下,产量和压力形式将表现出不同, Okouma M V 等提出了3 种图形判断法进行诊断[2]。
图形法1:标准化产量与产量标准化压降关 系图
| $\frac{q}{{{q}_{\text{i}}}}\sim \frac{\vartriangle p}{q}$ | (5) |
式中:q-产气量,×104 m3/d
qi-初始产气量,×104 m3/d;
Δp-生产压差,MPa。
图形法2:产量标准化压降与时间平方根关 系图
| $\frac{\vartriangle p}{q}\sim \sqrt{t}$ | (6) |
式中:t- 生产时间,d。
图形法3:产量标准化压降微分与物质平衡时 间双对数关系图
| $t\frac{\text{d}}{\text{d}t}\left[ \frac{\vartriangle p}{q} \right]\sim {{t}_{\text{mb}}}$ | (7) |
式中:tmb 物质平衡时间(累产气量/日产气量),d。
为了验证该方法是否适用,我们使用了3.4 节 中数值模拟生成的压力和产量数据进行分析,分析 结果如图 9~ 图 11。
 |
| 图9 标准化产量与产量标准化压降关系图 Fig. 9 Change in rate versus rate normalized pressure drop |
 |
| 图10 产量标准化压降与平方根时间关系图 Fig. 10 Rate normalized pressure drop versus square root of production time |
 |
| 图11 产量标准化压降与物质平衡时间关系图 Fig. 11 Rate normalized pressure drop derivative versus material balance time |
从图 9 中可以清楚地观察到,对于初期高配产 方案而言,在相同产量标准化压降条件下,产量递 减量更大。
图 10 为产量标准化压降与时间平方根的关系 图,该图是基于线性流理论创建的,初期低配产方 案具有一个较低的产量标准化压降数据,说明了具 有更高的生产能力。
从图 11 可以看出:初期低配产方案的产量标准 化压降微分数据点较低,该图可以认为是一个类似 于试井分析的图形,产量标准化压降与物质平衡时 间的双对数图形。
3 种图形判断法得出的结果均说明前期低配产 生产能力强于高配产。该结论和数模模拟结果一 致,说明图形判断法可以识别由于配产过大导致的 渗透率快速下降而影响生产的情况。值得说明的 是,这只是一种判断方法,在选择对比井的时候,需 要选择地质条件、工艺水平相当的井进行比较。
5 结论(1)页岩储层和人工压裂缝物理性质存在巨大 差别,进行应力敏感研究时应分开进行研究。通常, 压裂缝应力敏感强于储层应力敏感。
(2)应力敏感强弱主要跟地层的岩石力学性质 有关,即高泊松比和低杨氏模量的储层具有更强的 应力敏感,而与地层岩石初始渗透率无直接关系。
(3)压裂缝中支撑剂属于疏松不稳定介质,由 于破碎、嵌入储层或因产气量太大而运移,导致了 不同生产模式下应力敏感曲线不同,同时塑性较强 的地层压裂缝的应力敏感更强。
(4)数值模拟表明:应力敏感越强,最终采气量 越低;不同配产方案下采用相同的应力敏感方程模 拟,配产对最终的采气量影响不大,限产显得并不 必要,但若考虑稳产,仍然可以适当控制气井产量。
(5)如果不同配产模式下应力敏感衰竭方程不 同,数值模拟结果显示,适当限产对提高页岩气最 终采气量有利。
(6)诊断曲线可以诊断识别实际页岩气井是否 因为配产不合理引起生产能力下降,对页岩气藏合 理配产具有一定指导意义。
| [1] | WANG J, LIU Y. Simulation based well performance modeling in Haynesville shale reservoir[C]. SPE 142740, 2011. |
| [2] | OKOUMA M V,GUILLOT F,SARFARE M,et al. Estimated ultimate recovery(EUR) as a function of production practices in the Haynesville shale[C]. SPE 147623, 2011. |
| [3] | BAIHLY J D, ALTMAN R M, MALPANI R, et al. Shale gas production decline trend comparison over time and basins[C]. SPE 135555, 2010. |
| [4] | MILLER R S, CONWAY M, SALTER G. Pressuredependent permeability in shale reservoirs implication for estimated ultimate recovery[C]. AAPG Search and Discovery Article #90122, AAPG Hedberg Conference, Texas, 2010. |
| [5] |
李传亮. 低渗透储层不存在强应力敏感[J].
石油钻采工艺, 2005, 27 (4) : 61 –63.
LI Chuanliang. Low permeability rocks are less sensitive to stress[J]. Oil Drilling & Production Technology, 2005, 27 (4) : 61 –63. |
| [6] |
李闽, 肖文联, 赵春兰, 等. 不能用净应力评价低渗砂岩岩石应力敏感性[J].
西南石油大学学报(自然科学版), 2009, 31 (5) : 183 –186.
LI Min, XIAO Wenlian, ZHAO Chunlan, et al. Net stress can not be used to evaluate the stress sensitivity in the low permeability sandstone[J]. Journal of Southwest Petroleum University(Science& Technology Edition), 2009, 31 (5) : 183 –186. |
| [7] |
肖文联, 李闽, 赵金洲, 等. 低渗致密砂岩渗透率应力敏感性试验研究[J].
岩土力学, 2010, 31 (3) : 775 –779.
XIAO Wenlian, LI Min, ZHAO Jinhou, et al. Laboratory study of stress sensitivity to permeability in tight sandstone[J]. Rock and Soil Mechanics, 2010, 31 (3) : 775 –779. |
| [8] |
李传亮. 储层岩石的应力敏感性评价方法[J].
大庆石油地质与开发, 2006, 25 (1) : 40 –42.
LI Chuanliang. Evaluation method for stress sensitivity of reservoir rock[J]. Petroleum Geology and Oilfield Development in Daqing, 2006, 25 (1) : 40 –42. |
| [9] |
杨胜来, 王小强, 汪德刚, 等. 异常高压气藏岩石应力敏感性实验与模型研究[J].
天然气工业, 2005, 25 (2) : 107 –109.
YANG Shenglai, WANG Xiaoqiang, WANG Degang, et al. Experiment and model of rock stress sensitivity for abnormal high pressure gas reservoirs[J]. Natural Gas Industry, 2005, 25 (2) : 107 –109. |
| [10] | ADDIS M A. The stress-depletion response of reservoirs[C]. SPE 38720, 1997. |
| [11] | PALMER I, MANSOORI J. How permeability depends on stress and pore pressure in coalbeds:A new model[C]. SPE 36737, 1996. |
| [12] | FRIEDEL T. Numerical simulation of production from tight-gas reservoirs by advanced stimulation technologies[D]. Freiberg:TU Bergakademie, 2004. |
| [13] | JAYAKUMAR R,SAHAI V,BOULIS A. A better understanding of finite element simulation for shale gas reservoirs through a series of different case histories[C]. SPE 142464, 2011. |
| [14] |
罗瑞兰, 雷群, 范继武, 等. 应力敏感对致密压裂气井生产的影响[J].
重庆大学学报, 2011, 34 (2) : 95 –99.
LUO Ruilan, LEI Qun, FAN Jiwu, et al. The influence of stress sensitivity on production of hydraulically-fractured tight has wells[J]. Journal of Chongqing University, 2011, 34 (2) : 95 –99. |
| [15] |
温庆志, 张士诚, 王雷, 等. 支撑剂嵌入对裂缝长期导流能力的影响研究[J].
天然气工业, 2005, 25 (5) : 65 –68.
WEN Qingzhi, ZHANG Shicheng, WANG Lei, et al. Influence of proppant embedment on fracture loner termflow conductivity[J]. Natural Gas Industry, 2005, 25 (5) : 65 –68. |
| [16] |
宋军正, 郭建春. 压裂气井出砂机理研究[J].
钻采工艺, 2005, 28 (2) : 20 –21.
SONG Junzheng, GUO Jianchun. Mechanism study on sand production of fracturing gas well[J]. Drilling & Production Technology, 2005, 28 (2) : 20 –21. |
 2016, Vol. 38
2016, Vol. 38


