2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500;
3. 中国石油西南油气田公司, 四川 成都 610051
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. Southwest Oil and Gas Field Company Co. Ltd., CNPC, Chengdu, Sichuan 610051, China
压裂是油田一种重要的增产措施,选择合适的 井进行压裂作业可以提高油田的经济效益。压裂作 业费用十分昂贵,对储层质量的准确评价可以显著 提高改造成功率和经济效益[1-5]。压裂井质量评价 结果的可靠程度取决于评价数据准确性和评价方法 科学性。储层质量是由各种评价因素组成的复杂系 统,并且各因素之间具有不同程度相关性,每一因 素都只能从某一方面反映储层质量,采用单因素作 评价具有很大偏差[6-10]。压裂井储层质量评价对象 可以分为储层的储集性能和流动性能两个方面[11], 具体又可以进一步细分为储层岩性、沉积相、成岩 物理化学作用、储层物性等具体内容,而每个项目 中通常又包括多个参数,采用常规的回归分析等方 法基本无法对储层进行合理的分类评价。此外,压 裂井储层质量评价还存在模糊性的问题:各类储层 单因素的取值由于受到实验误差、计算分析等误差, 不一定真实反映了该参数在储层条件下的真实数 值;其次,用来对储层质量进行综合评价的众多因 素反映在具体某一口中时,可能出现各类参数的数 值大小不一致的现象,可能某一口井同时存在各类 参数既有“优”、“良”,又有“中”、“差”等评价,多 项参数交织在一起很难进行有效的评判和比较,对 储层质量的最终评价通常会出现“亦此亦彼”的模 糊结果况。由此可见,采用表征确定性问题的经典 数学方法来进行压裂井储层质量综合评价这个具有 显著模糊性的问题时存在明显的缺陷。
模糊数学是解决压裂井储层质量综合评价的有 效方法,它应用隶属函数来描述储层质量评价各参 数取值区间界限不明确的问题。文献[12-14]采用 人工神经网络和人工智能的方法对压裂井储层进 行评价,取得了比较满意的效果,但是在实际应用 过程中,权重数的确定受到经验和主观性判断的影 响。方差分析法和主成分分析法能够有效确定各影 响因素的权重,但是这类方法要求有大量的样本数 据、并且要求这些样本数据特征要服从一定的概率 分布[15-16]。灰色关联法可以有效解决上述难题[17], 具有良好的应用前景。笔者在文中通过引入灰色 关联分析理论来确定影响储层质量评价各要素的 权重;进一步将模糊数学与灰色关联分析方法相结 合,并且通过建立多层次指标体系,发展形成了具 体层次性的模糊灰色理论分析的综合评价方法,最 终得到一个反映储层质量性能的唯一一个综合评价 指标,并依据它来对储层进行分类。通过将模糊数 学、灰色关联理论和层次分析相结合的方法,显著 降低了人为主观因素的干预,提高了评价精度。
1 储层质量综合评价原理为了客观公正地评价压裂井储层质量,首先必 须选择建立评价储层优劣的参数和参数体系。依 据压裂井储层质量评价的概念和特征,将其分解为 储集能力、流动能力2 个基本要素。并进一步对这 两个要素进一步细化,结合储层综合评价的实际情 况,按照科学性、系统性等基本原理,建立起如图 1 所示的包含1 个目标层、2 个要素层、3 个指标层的 层次指标体系,见图 1。
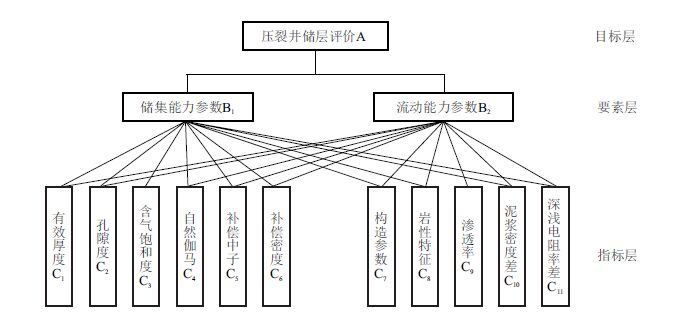 |
| 图1 压裂井储层评价层次结构模型 Fig. 1 Hierarchical structure model of fracturing wells quality |
将每个要素层下的若干指标层因素进行综合以后就得到了上层因素的特征,如有效厚度、孔隙度、含气饱和度、自然伽马、补偿中子、补偿密度加起来 即表现为储层的储集能力。也即是说,指标层集合 构成了要素层的各个因素,进而组成了整个要素层。 然而,情况并不如这样简单,指标层并不只是对分出 它的要素层有贡献,它还可能会对上一层次中别的 要素层有贡献。比如,有效厚度既反映了储层的储 集能力、又反映了流动能力特征。因为储层如果越 厚,在地应力作用下,越不容易产生裂缝,同时也会 降低储层的渗流能力。同样的,地层构造参数同时 也会对流动能力和储集能力同时产生贡献,这样就 得到了复杂的递阶层次结构图。图 1 实质上也反映 出为了真实反映一口压裂井储层质量的优劣,必须 同时综合储集能力、流动能力特征参数的共同影响。
2 模糊综合评判数学模型 2.1 评价因素集因素就是参与储层评价时具体采用的指标,在 压裂井储层质量评价过程中,评价因素集就是用来 表征参储层质量的n个因素所组成的模糊子集合, 数学表达为u = (u1, u2,…, un)。
2.2 评价集评价集合表示为v = (v1, v2,…, vm),它是一个 全序集,即对v 中任意两个评价间存在等级差别。v 是u 中评价因子相应的评价标准集合。对压裂井储 层质量进行评价时,v 即是各个评价因素相应的储 层质量等级(Ⅰ 、Ⅱ 、Ⅲ、Ⅳ级等)的集合。
2.3 评价因素的模糊权向量在压裂井储层质量评价时,考虑到各因素对储 层质量评价结果的影响不完全一致,因此必须对每 个因素ui 赋予一个独立的权重ai(i = 1, 2,…n) 从而 构成权重集A。准确量化指标的权重确定将会直接 影响量化结果,这里采用灰色系统理论法中的灰色 关联分析来确定权重。使用灰色关联理论确定权重 包括3 个步骤[17]:(1)确定各个因素及无阻流量,并 将其进行归一化处理;(2)计算各个因素与无阻流 量间的关联系数;(3)进一步求取关联度得出各因 素所占的权重系数[18]。
2.4 单因素评价矩阵 2.4.1 确定隶属函数隶属函数是将模糊数学应用于压裂井储层质量 评价的基石。它是以其中某一个因素ui 出发进行评价,以确定评价对象评价元素vj的隶属度称之为 单因素评价隶属函数。根据现场数据统计结果,采 用正态分布隶属函数[19]
| ${{u}_{v}}\left( d \right)={{\text{e}}^{-{{\left[ \left( d-a \right)/b \right]}^{2}}}}$ | (1) |
式中: uv-隶属函数,无因次;
d-评判因素的具体数值,无因次;
a,b-指标参数,无因次;
下标v评语等级,无因次。
其中,隶属度函数为
| ${{u}_{vj}}\left( {{d}_{i}} \right)={{\text{e}}^{-{{\left[ \left( {{d}_{i}}-a \right)/b \right]}^{2}}}}$ | (2) |
式中: uvj-(di) di 在评语等级vj 上的隶属度,无因次; di-第i 个评判因素的具体数值,无因次。
由式(2)可知:当dj = a 时,uvj (a) = 1,表示该 参数属于某一个评价等级的概率及隶属度最大,所 以a 为某等级的数学期望,即
| $a=\left( {{d}_{1}}+{{d}_{2}} \right)/2$ | (3) |
式中:d1,d2-第j 个评语等级区间的上、下限值, 无因次。
a 点称为过渡点,一般取过渡点的隶属度为 0.5,它同时是某一个参数前一评语等级的下限,又 是后一评语等级的上限,即
| ${{u}_{vj}}\left( {{d}_{j1}} \right)={{\text{e}}^{-{{\left[ \left( {{d}_{j1}}-{{d}_{j2}} \right)/\left( 2b \right) \right]}^{2}}}}$ | (4) |
| $b=\sqrt{{{\left( {{d}_{j1}}-{{d}_{j2}} \right)}^{2}}/\left( 4\ln 2 \right)}$ | (5) |
a,b值确定后,即可确定唯一明确的隶属函 数关系。第i 个因素ui 的评价结果模糊集合为 Ri = (ri1, ri2, ri3,…, rim)。
2.4.2 单因素评价
通过上面的计算,就可以得到每个因素的单因 素模糊评价集。在压裂井储层质量评价过程中,考 虑总共有m 个评价等级、n项评价指标的储层评价 标准,则可得到n
| $R={{u}_{vj}}\left( {{d}_{i}} \right)=\left[ \begin{align} & \begin{matrix} {{r}_{11}} & {{r}_{12}} & \cdots & {{r}_{1m}} \\ \end{matrix} \\ & \begin{matrix} {{r}_{21}} & {{r}_{22}} & \cdots & {{r}_{2m}} \\ \end{matrix} \\ & \begin{matrix} \cdots & \cdots & \cdots & \cdots \\ \end{matrix} \\ & \begin{matrix} {{r}_{n1}} & {{r}_{n2}} & \cdots & {{r}_{nm}} \\ \end{matrix} \\ \end{align} \right]$ | (6) |
单因素评价结果只从一个因素出发对储层质量 的优劣进行了评价,它不能完全反映出各个因素对 储层质量评价的综合影响,也就不能得出具体的综合评价结果。因此需要通过矩阵乘积求和算法,将模糊权向量矩阵A与单因素模糊评价矩阵R进行复 合,就可以得到考虑各个要素综合影响的模糊综合 评价向量B
| $\begin{array}{l} B = \left( {{b_1},{b_2}, \cdots ,{b_m}} \right) = A \cdot R = \\ \left( {{a_1},{a_2}, \cdots ,{a_m}} \right) \cdot \left[ \begin{array}{l} \begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}} \end{array}\\ \begin{array}{*{20}{c}} {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}} \end{array}\\ \begin{array}{*{20}{c}} \cdots & \cdots & \cdots & \cdots \end{array}\\ \begin{array}{*{20}{c}} {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array} \end{array} \right] \end{array}$ | (7) |
其中:bj-综合考虑各个因素影响时,对第j个因 素的隶属程度的评价指标,无因次。
为了方便进一步应用,这里将各隶属度加权平 均转化为直观的模糊评分
| $x=\sum\limits_{j=1}^{m}{\left( {{b}_{j}}\times {{v}_{j}} \right)}/\sum\limits_{j=1}^{m}{{{b}_{j}}}$ | (8) |
某为岩性圈闭凝析油气藏在局部潜伏构造上有 比较发育的天然裂缝和微孔隙,储层非均质性强, 前期改造井的有效率仅为67%,经济效益较差,需 要建立一种有效的压裂井储层质量评价来提高该凝 析油气藏的压裂改造效果。
3.2 评价因素选择压裂井储层质量评价的主要工作为压裂效果评 价与预测。由于该气田已经有了相当数量的已压裂 施工井,考虑该区块后续的压裂井在改造模式、压 裂液及支撑剂施工材料不变的情况下,可以充分利 用前期压裂井的钻井、录井、测井、压裂施工参数以 及压裂后的生产动态数据进行储层质量评价,提高 压裂改造效果的产量。在众多影响压裂效果的因素 中,有些参数对压裂效果影响显著,有些参数对压 裂效果影响不明显,因此,需要尽可能地充分考虑 影响压裂井效果的多种参数综合影响。通过采用相 关性分析,并结合现场专家、技术人员对该区块的 储层特征和生产效果认识,最终确定了了11 个研究 参数:有效厚度、孔隙度、含气饱和度、自然伽马、补 偿中子、补偿密度、构造参数、岩性特征、渗透率、泥 浆密度差和深浅电阻率差。根据理论分析和数理统 计结果,将每项分级区间值列于表 1。
| 表1 因素选择及分级区间 Table 1 Factors selection and grade levels |
由于压裂井的储层质量是一个具有模糊性质的 概念,考虑到储层质量的评价是一个多层次、多目 标、多因素控制的复杂模糊系统,所以评价的分级 标准也应该具有模糊的特性。根据前期压裂井改造 后的无阻流量统计结果,结合现场专家意见,将压 裂井的储层质量评价化分为Ⅰ、Ⅱ、Ⅲ和Ⅳ 共4个等级。
3.4 模糊权重集利用收集到的前期压裂井样本资料,按照前文 所述方法,利用灰色关联度理论计算一级评判权重
| $\begin{align} & 向量 \\ & {{A}_{1}}=\left[ 厚度, 孔隙度, 含气饱和度, 补偿中子,自然伽马, 补偿密度 \right]= \\ & \left[ \text{0}\text{.1585,0}\text{.1701, 0}\text{.1686,0}\text{.1748,0}\text{.1612,0}\text{.1668} \right] \\ \end{align}$ | (9) |
| $\begin{align} & {{A}_{2}}=\left[ 渗透率, 构造参数, 岩性特征, 泥浆密度差, 深浅电阻率差 \right]= \\ & \left[ 0.1989,0.2379,0.1782,0.1866,0.1985 \right] \\ \end{align}$ | (10) |
| $\begin{align} & 二级评判权重向量 \\ & A=\left[ \begin{matrix} {{A}_{1}} & {{A}_{2}} \\ \end{matrix} \right]=\left[ 0.5334,0.4666 \right] \\ \end{align}$ | (11) |
取H-124 井作为样本,根据所建立的评价因素 集合评语集和隶属函数数学模型求取各参数的隶属 度,计算结果见表 2。
| 表2 H-124 井实测数据 Table 2 Measured data of H-124 |
由式(7)及表 2 数据可得每一因素在各个区间 的隶属度
| ${{R}_{1}}=\left[ \begin{align} & \begin{matrix} 0.0029 & 0.5704 & 0.43230 & 0 \\ \end{matrix} \\ & \begin{matrix} 0.0072 & 0.7340 & 0.29240 & 0.00045 \\ \end{matrix} \\ & \begin{matrix} 0 & 0 & 0.0147 & 0.85990 \\ \end{matrix} \\ & \begin{matrix} 0.2251 & 0.8211 & 0.01200 & 0 \\ \end{matrix} \\ & \begin{matrix} 0.1515 & 0.9186 & 0.02180 & 0 \\ \end{matrix} \\ & \begin{matrix} 0 & 0 & 0.00195 & 0.50000 \\ \end{matrix} \\ \end{align} \right]$ | (12) |
| ${{R}_{2}}=\left[ \begin{matrix} 0.25700 & 0.9727 & 0.0131 & 0 \\ 0.90480 & 0.0526 & 0 & 0 \\ 0.87440 & 0 & 0 & 0 \\ 0.00195 & 0.5000 & 0.5000 & 0.4280 \\ 0.041800 & 0.9865 & 0.0910 & 0 \\ \end{matrix} \right]$ | (13) |
由B1 = A1·R1,B2 = A2·R2,可得二级评判的模糊矩阵
| $R=\left[ \begin{matrix} 0.0655 & 0.5069 & 0.1266 & 0.2285 \\ 0.4039 & 0.4951 & 0.1140 & 0.0800 \\ \end{matrix} \right]$ | (14) |
H-124 井的隶属度为
| $B=A\cdot R\left[ \begin{matrix} 0.2360 & 0.5014 & 0.1207 & 0.1592 \\ \end{matrix} \right]$ | (15) |
计算模糊评分,得
| $x=\sum\limits_{j=1}^{4}{\left( {{b}_{j}}\times {{v}_{j}} \right)/\sum\limits_{j=1}^{4}{{{b}_{j}}}}=71$ | (16) |
根据井计算的隶属度和模糊评分,H-124 井为Ⅱ类储层。该井压裂前射孔后无产量,压裂后获得 无阻流量8.61×104 m3/d,增产效果显著,与评判结 果相符。同样方法对该区块其他3 口井进行了计 算,也验证了结果的合理性(表 3)。
| 表3 4 口井基础参数表及评价结果 Table 3 Basic parameters and evaluation results of four wells |
从表 3 可见,模糊评分越高,压裂井储层质量越 好。这与无阻流量越大相吻合,说明采用模糊数学 和灰色理论对压裂井储层质量评价结果是可靠的, 能够很好地定量解决压裂井储层质量评价问题。
4 结语(1)将压裂井储层质量评价指标细分为储集能 力和流动能力两类因素,引入了模糊综合评判与灰 色关联分析理论,建立了多层次模糊灰色关联分析 综合评价理论,避免可能产生的人为主观因素,提 高了评价精度。
(2)综合评价理论在某岩性圈闭非均质气藏进 行了现场应用,通过特征参数进行综合评价,结果 与实际产量基本吻合,验证了模型的可靠性,对类 似储层评价具有指导意义。
| [1] | 刘艳, 高有瑞. 已探明未开发石油储量评价的模糊数学方法[J]. 石油勘探与开发, 1993, 20 (1) : 105 –109. |
| [2] |
曾凡辉, 刘林, 王文耀, 等. 乌里雅斯太凹陷压裂井选井选层研究[J].
西南石油大学学报(自然科学版), 2009, 31 (5) : 45 –49.
ZENG Fanhui, LIU Lin, WANG Wenyao, et al. The well and layer selection in fracturing in ulyastai sag[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2009, 31 (5) : 45 –49. |
| [3] | 宋永, 刘春林, 陆仁桓. 影响油层压裂效果的因素分析[J]. 大庆石油地质与开发, 1995, 14 (2) : 38 –41. |
| [4] | 肖芳淳. 压裂酸化中选层的模糊物元评价分析[J]. 石油钻采工艺, 1996, 18 (6) : 49 –53. |
| [5] |
石战战, 贺振华, 文晓涛, 等. 一种基于EMD和GHT的储层识别方法[J].
岩性油气藏, 2011, 23 (3) : 102 –109.
SHI Zhanzhan, HE Zhenhua, WEN Xiaotao, et al. Reservoir detection based on EMD and GHT[J]. Lithologic Reservoirs, 2011, 23 (3) : 102 –109. |
| [6] |
汪洋, 王桂成, 王羽君, 等. 鄂尔多斯盆地郑庄油区延长组长6油层组储层特征[J].
岩性油气藏, 2010, 22 (3) : 48 –52.
WANG Yang, WANG Guicheng, WANG Yujun, et al. Characteristics of Chang 6 reservoir in Zhengzhuang oil region of Ordos Basin[J]. Lithologic Reservoirs, 2010, 22 (3) : 48 –52. |
| [7] |
侯斌, 桂志先, 许辉群, 等. 应用多属性神经网络方法预测油气[J].
岩性油气藏, 2010, 22 (3) : 118 –121.
HOU Bin, GUI Zhixian, XU Huiqun, et al. Application of multi-attribute and neural network method to hydrocarbon reservoir prediction[J]. Lithologic Reservoirs, 2010, 22 (3) : 118 –121. |
| [8] | 黄龙, 田景春, 肖玲, 等. 鄂尔多斯盆地富县地区长6砂岩储层特征及评价[J]. 岩性油气藏, 2008, 20 (1) : 84 –88. |
| [9] | 滕团余, 余建平, 崔海峰, 等. YH地区碳酸盐岩储层预测方法研究及应用[J]. 岩性油气藏, 2008, 20 (2) : 119 –123. |
| [10] | 郭建春, 吴建发, 赵金洲. 压裂酸化选井的人工神经网络软件研制[J]. 天然气工业, 2004, 24 (11) : 67 –69. |
| [11] | 俞绍诚. 水力压裂技术手册[M]. 北京: 石油工业出版社, 2010 . |
| [12] | SHELLEY R F. Artificial neural networks identify restimulation candidate in the red oak field[C]. SPE 52190, 1999. |
| [13] | MOHAGHEGH S, REEVES S, HILL D. Development of an intelligent systems approach for restimulation candidate selection[C]. SPE 59767, 2000. |
| [14] | OBERWINKLER C,ECONOMIDES M J. The definitive identification of candidate wells for refracturing[C]. SPE 84211, 2003. |
| [15] |
胡庆军, 吴翊. 主方差分析方法[J].
国防科技大学学报, 2000, 22 (2) : 117 –120.
HU Qingjun, WU Yi. The method of principal variance analysis[J]. Journal of National University of Defense Technology, 2000, 22 (2) : 117 –120. |
| [16] | 陈伟. 主成份分析法用于评价需注意的若干问题[J]. 人类工效学, 2002, 8 (1) : 30 –33. |
| [17] | 邓聚龙. 灰色理论基础[M]. 武汉: 华中科技大学出版社, 2002 . |
| [18] | 张迎朝, 时志强. 用灰色相对变率关联度分析法确定影响油气井产量因素的权重[J]. 石油勘探与开发, 1998, 25 (2) : 73 –74. |
| [19] | 汪培庄. 模糊集合论及其应用[M]. 上海: 上海科学技术出版社, 1983 . |
 2016, Vol. 38
2016, Vol. 38


