2. "提高石油采收率"国家重点实验室·中国石油勘探开发研究院, 北京 海淀 100083;
3. 中国石油新疆油田公司勘探开发研究院, 新疆 克拉玛依 834000
2. State Key Laboratory of EOR, Research Institute of Petroleum Exploration and Development, Petrochina, Haidian, Beijing 100083, China;
3. Xinjiang Oilfield Company, Petrochina, Karamay, Xinjiang 834000, China
蒸汽辅助重力泄油技术(SAGD,Steam assisted gravity drainage)在加拿大油砂矿区已经成熟配套,并实现了大规模商业化应用,具有稳产期长,稳产期产量水平高、采收率高等突出优势。自2008年以来,在中国新疆、辽河等稠油油区开展了大规模的双水平井SAGD工业化试验,目前已转入SAGD商业化生产井对100个以上,对实现稠油的持续稳产以及中国能源战略目标的实现具有重要的意义。SAGD的全生命周期分为4个阶段:循环预热阶段、蒸汽腔上升阶段、蒸汽腔扩展阶段、蒸汽腔下降阶段[1-3]。前期试验结果与跟踪分析表明,影响SAGD产量的关键因素在于水平段蒸汽腔的发育规模。而对蒸汽腔发育规模最重要的影响在于转SAGD生产之前注采井对水平段之间储层的均匀预热程度。转入SAGD生产之前,通常要求循环预热井间储层温度达到140 ℃以上、或原油黏度达到100 mPa$\cdot$s以下。因此,准确预测注采井间储层温度,是判断循环预热是否达到要求、并确定转SAGD生产时机的技术关键[4-5]。
判断SAGD循环预热过程中注采井间储层温度有两种方法:数值模拟法和解析解法。通常,SAGD注蒸汽循环预热过程中,注汽井与生产井一般下入平行双油管(长油管下入脚尖,短油管下入脚跟),循环预热过程中,长油管注汽,短油管排液[6-7]。由于对于注汽井与生产井,每口井均同时有套管(水平段为筛管)、长油管、短油管,因此SAGD管柱结构较为复杂,CMG公司为此开发了FLEX WELLBORE模块,专门用于处理SAGD复杂管柱结构,但在数值模拟过程中,复杂管流条件下的SAGD双油管数值模型复杂,模拟计算速度较慢,计算过程中迭代次数多,难以快速得到计算结果。
相比数值模拟而言,解析解具有方便快捷等优势,前人也曾经对SAGD循环预热过程中注采井水平段之间储层的升温情况建立过解析公式[4-6],但由于其只考虑储层岩石基质的热物性特征,在SAGD前期开发过程中,与SAGD试验区跟踪数值模拟拟合结果对比表明,其预测精度较差。在实际储层条件下,储层岩石内部还饱和了油水,因此对于复杂的油水岩石介质,目前尚未建立考虑多介质、多相流体、孔隙度与含油饱和度等共同影响的综合传热解析新模型。
为此,本文充分考虑实际储层多孔介质中岩石、原油、地层水传热与热扩散性能的不同特征,建立了考虑油水岩石的多介质多相流体综合传热解析新模型,并以某油区实际的井下测温数据、油水岩石热物性参数等为基础,进行了注蒸汽循环预热阶段注采井水平段之间温度变化测算,并与数值模拟计算结果进行了对比,验证了模型的准确性与实用性。
1 多介质多相流综合传热解析新模型 1.1 单一热源传热模型在任意二维平面上的任意一点,被该平面上单一热源加热时(热源温度为$T_{\rm{s}}$,原始温度为$T_{\rm{i}}$,热流入速度为q),该点被热源加热过程中温度T随时间t的变化可表示为[4-6]
| $T={{T}_{\text{i}}}-\frac{q}{4\pi k}{{E}_{\text{i}}}\left( -\frac{{{r}^{2}}}{4\lambda \alpha t} \right)$ | (1) |
在双水平井循环预热过程中,在垂直于注汽井与生产井的水平段的二维平面上,注汽井与生产井水平段井筒刚好代表了该二维平面上的两个热源(图 1)。
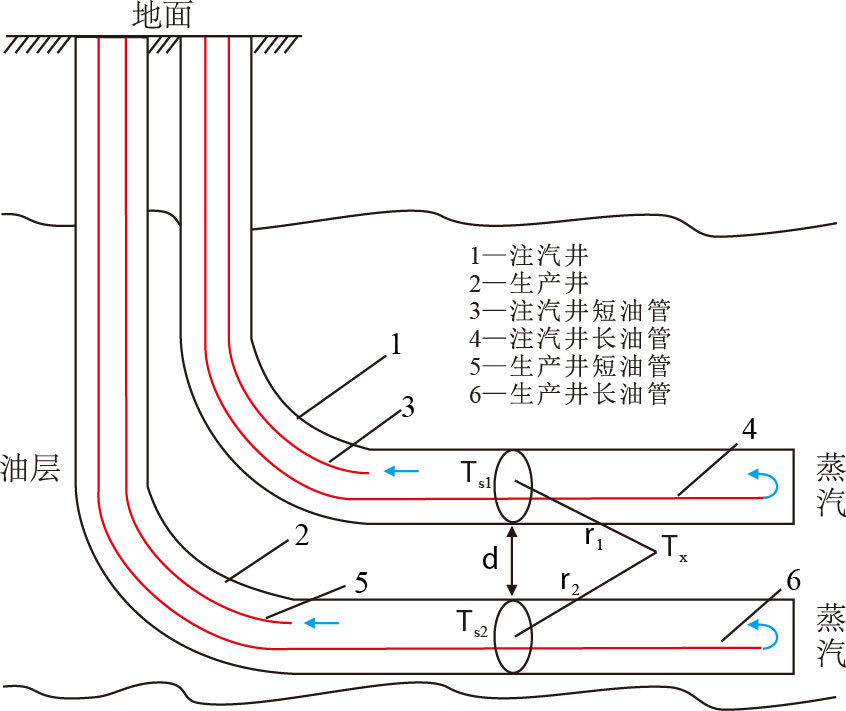 |
| 图1 双水平井水平段切片二维平面注汽井与生产井井筒位置示意图 Fig. 1 Injector and producer wellbores in 2D cross-section map of dual-horizontal SAGD |
其中,注汽井井筒半径为$r_{\rm{w1}}$,注汽循环预热的温度为$T_{\rm{s1}}$,热流过该点的速度为$q_1$;生产井井筒半径为$r_{\rm{w2}}$,注汽循环预热的温度为$T_{\rm{s2}}$,热流过该点的速度为$q_2$;根据热源叠加理论,该二维平面上任意点x升高的温度,应等于该两个热源传热升温之和
| $\Delta {T_x}{\rm{ = }}\Delta {T_{{x_1}}}{\rm{ + }}\Delta {T_{{x_2}}}{\rm{ = }}{T_{{x_1}}} - {T_{\rm{i}}}{\rm{ + }}{T_{{x_2}}} - {T_{\rm{i}}}$ | (2) |
对于注汽井井筒热源,对任一点x的升温贡献值为
| $\Delta {T_{{x_1}}}={T_{{x_1}}} - {T_{\rm{i}}}= - {\dfrac{{{q_1}}}{{4\pi {k_1}}}} {E_{\rm{i}}}\left( { - \dfrac{{{r_1}^2}}{{4\lambda {\alpha _1}{t_1}}}} \right)$ | (3) |
对于生产井井筒热源,对任一点x的升温贡献值为
| $\Delta {T_{{x_2}}}={T_{{x_2}}} - {T_{\rm{i}}}= - {\dfrac{{{q_2}}}{{4\pi {k_2}}}} {E_{\rm{i}}}\left( { - \dfrac{{{r_2}^2}}{{4\lambda {\alpha _2}{t_2}}}} \right)$ | (4) |
因此,该二维平面上任意点x升高的温度
| $\Delta {T_x}\!=\!- {\dfrac{{{q_1}}}{{4\pi {k_1}}}} {E_{\rm{i}}}\left( {\dfrac{{-{r_1}^2}}{{4\lambda {\alpha _1}{t_1}}}} \right) - {\dfrac{{{q_2}}}{{4\pi {k_2}}}} {E_{\rm{i}}}\left( { \dfrac{-{{r_2}^2}}{{4\lambda {\alpha _2}{t_2}}}} \right)$ | (5) |
边界条件1:对于该二维平面注汽井井筒外侧壁,$r_1=r_{\rm{w1}}$,$r_2=d$,因此,该点升温值表示为
| $\Delta {T_{\rm{s1}}}\!=\!- {\dfrac{{{q_1}}}{{4\pi {k_1}}}} {E_{\rm{i}}}\left( { \dfrac{-{{r_{\rm{w1}}}^2}}{{4\lambda {\alpha _1}{t_1}}}} \right) - {\dfrac{{{q_2}}}{{4\pi {k_2}}}} {E_{\rm{i}}}\left( { \dfrac{{- {d}^2}}{{4\lambda {\alpha _2}{t_2}}}} \right)$ | (6) |
边界条件2:对于该二维平面生产井井筒外侧壁,$r_2=r_{\rm{w2}}$,$r_1=d$,因此,该点升温值表示为
| $\Delta {T_{\rm{s2}}}\!=\!- {\dfrac{{{q_1}}}{{4\pi {k_1}}}} {E_{\rm{i}}}\left( { \dfrac{-{{d}^2}}{{4\lambda {\alpha _1}{t_1}}}} \right) - {\dfrac{{{q_2}}}{{4\pi {k_2}}}} {E_{\rm{i}}}\left( { \dfrac{-{{r_{\rm{w2}}}^2}}{{4\lambda {\alpha _2}{t_2}}}} \right)$ | (7) |
联合式(5)、式(6)、式(7)求解,得到
| $\begin{align} & \Delta {{T}_{x}}=\frac{{{E}_{\text{i}}}\left( -\frac{{{r}_{1}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\left[\Delta {{T}_{\text{s2}}}{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)-\Delta {{T}_{\text{s1}}}{{E}_{i}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right) \right]}{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)}+ \\ & \frac{{{E}_{\text{i}}}\left( -\frac{{{r}_{2}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)\left[\Delta {{T}_{\text{s1}}}{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-\Delta {{T}_{\text{s2}}}{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right) \right]}{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)} \\ \end{align}$ | (8) |
双水平井SAGD注蒸汽循环预热过程中,对于注采井水平段中间位置,$r_1=r_2=d/2$,则有
| $\begin{align} & \Delta {{T}_{x}}=\frac{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{16\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\left[\Delta {{T}_{\text{s2}}}{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)-\Delta {{T}_{\text{s1}}}{{E}_{i}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right) \right]}{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)}+ \\ & \frac{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{16\lambda {{\alpha }_{2}}{{t}_{2}}} \right)\left[\Delta {{T}_{\text{s1}}}{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-\Delta {{T}_{\text{s2}}}{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right) \right]}{{{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{d}^{2}}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)-{{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w1}}}^{2}}{4\lambda {{\alpha }_{1}}{{t}_{1}}} \right)\cdot {{E}_{\text{i}}}\left( -\frac{{{r}_{\text{w2}}}^{2}}{4\lambda {{\alpha }_{2}}{{t}_{2}}} \right)} \\ \end{align}$ | (9) |
当注采井水平段之间距离恒定为d,注采井井筒尺寸相等$r_{\rm{w1}}=r_{\rm{w2}}=r_{\rm{w}}$,油层为均质油层$\alpha _1=\alpha _2=\alpha$,则式(9)可简化为
| $\Delta {T_x} = \dfrac{{\left( {\Delta {T_{{\rm{s1}}}} + \Delta {T_{{\rm{s2}}}}} \right) \cdot {E_{\rm{i}}}\left( { - \dfrac{{{d^2}}}{{16\lambda \alpha t}}} \right)}}{{{E_{\rm{i}}}\left( { - \dfrac{{{d^2}}}{{4\lambda \alpha t}}} \right) + {E_{\rm{i}}}\left( { - \dfrac{{{r_{\rm{w}}}^2}}{{4\lambda \alpha t}}} \right)}}$ | (10) |
但在实际油层多孔介质中,既存在岩石基质,也存在孔隙空间的原油与地层水,因此,热量在油层中的扩散,需要综合考虑岩石基质、原油与地层水的综合热扩散能力。由于岩石基质与原油、地层水之间的热扩散性能差别较大,因此只考虑油层岩石的热扩散,对计算结果影响较大。
同时,油层中不同位置含油饱和度、孔隙度等均不同,不同含油饱和度条件下的油水分布对综合热扩散能力影响较大;不同孔隙度下的基质含量与流体含量也不同。
基于上述情况,需要综合考虑油层传热介质、油层含油饱和度与孔隙度等物性对热扩散能力的综合影响,才能正确表征SAGD循环预热过程中,热量在油层中的真实传递情况。
为此,引入油层综合热扩散系数[7-13],其值等于导热系数除以密度与比热容的乘积
| ${\alpha _{{\rm{mix}}}} = \dfrac{{{\lambda _{\rm{mix}}}}}{{{\rho _{\rm{mix}}} \cdot {C_{\rm{mix}}}}}$ | (11) |
实际油层条件下的综合导热系数${\lambda _{\rm{mix}}}$为
| ${\lambda _{{\rm{mix}}}} = {\phi _{\rm{f}}} \cdot ({\lambda _{\rm{w}}} \cdot {S_{\rm{w}}} + {\lambda _{\rm{o}}} \cdot {S_{\rm{o}}}) + (1 - {\phi _{\rm{f}}}) \cdot {\lambda _{\rm{f}}}$ | (12) |
油层综合密度计算公式为
| ${\rho _{\rm{mix}}} = {\phi _{\rm{f}}} \cdot ({\rho _{\rm{w}}} \cdot {S_{\rm{w}}} + {\rho _{\rm{o}}} \cdot {S_{\rm{o}}}) + (1 - {\phi _{\rm{f}}}) \cdot {\rho _{\rm{f}}}$ | (13) |
油、水、基质共存条件下油层综合比热容的计算公式为
| ${C_{\rm{mix}}} = {f_{\rm{gr}}} \cdot {C_{\rm{f}}} + {f_{\rm{o}}} \cdot {C_{\rm{o}}} + {f_{\rm{w}}} \cdot {C_{\rm{w}}}$ | (14) |
由式(12)~式(14),实际油层条件下的综合热扩散系数计算公式为
| $\begin{align} & {{\alpha }_{\text{mix}}}=\frac{{{\phi }_{\text{f}}}({{\lambda }_{\text{w}}}{{S}_{\text{w}}}+{{\lambda }_{\text{o}}}{{S}_{\text{o}}})+(1-{{\phi }_{\text{f}}}){{\lambda }_{\text{f}}}}{{{\phi }_{\text{f}}}({{\rho }_{\text{w}}}{{S}_{\text{w}}}+{{\rho }_{\text{o}}}{{S}_{\text{o}}})+(1-{{\phi }_{\text{f}}}){{\rho }_{\text{f}}}}\cdot \\ & {{\left( {{f}_{\text{gr}}}{{C}_{\text{f}}}+{{f}_{\text{o}}}{{C}_{\text{o}}}+{{f}_{\text{w}}}{{C}_{\text{w}}} \right)}^{-1}} \\ \end{align}$ | (15) |
式(15)代入式(10),就可以得到在油层实际孔隙度、含油饱和度等条件下,双水平井SAGD循环预热过程中注采井水平段中间油层的传热升温解析模型
| $\Delta {T_x} = \dfrac{{\left( {\Delta {T_{{\rm{s1}}}} + \Delta {T_{{\rm{s2}}}}} \right) \cdot {E_{\rm{i}}}\left( { - \dfrac{{{d^2}}}{{16\lambda {\alpha _{{\rm{mix}}}}t}}} \right)}}{{{E_{\rm{i}}}\left( { - \dfrac{{{d^2}}}{{4\lambda {\alpha _{{\rm{mix}}}}t}}} \right) + {E_{\rm{i}}}\left( { - \dfrac{{{r_{\rm{w}}}^2}}{{4\lambda {\alpha _{{\rm{mix}}}}t}}} \right)}}$ | (16) |
在循环预热过程中,通过水平段内均匀分布的温度传感器,可分别得到注汽井水平段不同位置不同时刻的${T_{{\rm{s1}}}}$与生产井水平段不同位置不同时刻的${T_{{\rm{s2}}}}$。不同位置含油饱和度${S_{\rm{o}}}$、岩石基质密度${\rho _{\rm{f}}}$、岩石孔隙度${\phi _{\rm{f}}}$等,可以通过水平段测井解释得到。不同位置岩石的导热系数${\lambda _{\rm{f}}}$以及比热容${C _{\rm{o}}}$ 等可以通过录井与取芯化验分析得到。
2 循环预热模型实例验证以新疆某双水平井SAGD试验区的一典型井组为例,对上述解析模型进行验证。该井组注汽井与生产井水平段均下入均匀分布的7个温度传感器;温度传感器所在位置的油层岩性均为砂岩,通过水平段测井曲线解释温度传感器所在位置油层的孔隙度与含油饱和度;注汽井与生产井水平段筛管尺寸均为244.47 mm。
通过对温度传感器所在位置油层的录井与取芯化验分析,得到各位置油层岩石基质热物性参数。通过对试采油样与地层水进行PVT等测试分析,得到油层流体的PVT与热物性参数(表 1)。
| 表1 原油与地层水热物性参数表 Table 1 Thermal properties of oil and formation water |
根据物性参数,计算得到实际油层条件下的油层热物性参数以及综合热扩散系数见表 2。
| 表2 油层热物性参数以及综合热扩散系数 Table 2 Formation thermal properties and calculation results of integral thermal diffusivity |
模型计算条件为:SAGD循环预热过程中,注入蒸汽温度为250 ℃,注汽井与生产井的单井注汽速度均为100 t/d,井下监测数据表明,注汽循环7 d,注汽井与生产井水平段远端均见汽,即水平段井筒内温度均达到250 ℃。因此,以水平段井筒内温度均达到250 ℃为基础,对不同时刻注采井水平段井筒中间油层位置的温度进行测算。
2.1 新旧模型计算结果对比利用上述参数,测算了水平段远端见汽以后,在不同时刻,注采井水平段井间位置油层的温度变化(原始油藏温度15 ℃),并对原始模型(式(10))测算得到的温度变化值进行了对比。对比结果表明(表 3),本文提出的考虑油层孔隙度、含油饱和度、油水等多介质热物性特征参数的新模型(式(16))计算得到的注采井水平段中间位置升温值,普遍低于仅考虑油层岩石热物性参数的原始模型计算结果。其中,测点1井对中间升高温度的平均计算误差为0.40 ℃,测点3井对中间升高温度的平均计算误差为14.93 ℃,测点5井对中间升高温度的平均计算误差为10.57 ℃。
| 表3 原模型与新模型计算结果对比 Table 3 Formation thermal properties and calculation results of integral thermal diffusivity |
为验证本文提出的新模型计算结果准确性,采用CMG-STARS软件的FLEX WELLBORE模块,以上述实际油藏岩石、流体、以及管柱结构为基础,建立起双水平井SAGD循环预热数值模型。并以实际循环预热注汽与排液参数做为注采控制参数,对循环预热不同时刻的注采动态进行了历史拟合。在拟合完成后,对注采井水平段中间部位的温度场进行了提取,循环预热190 d的温度场剖面与测温点分布见图 2。
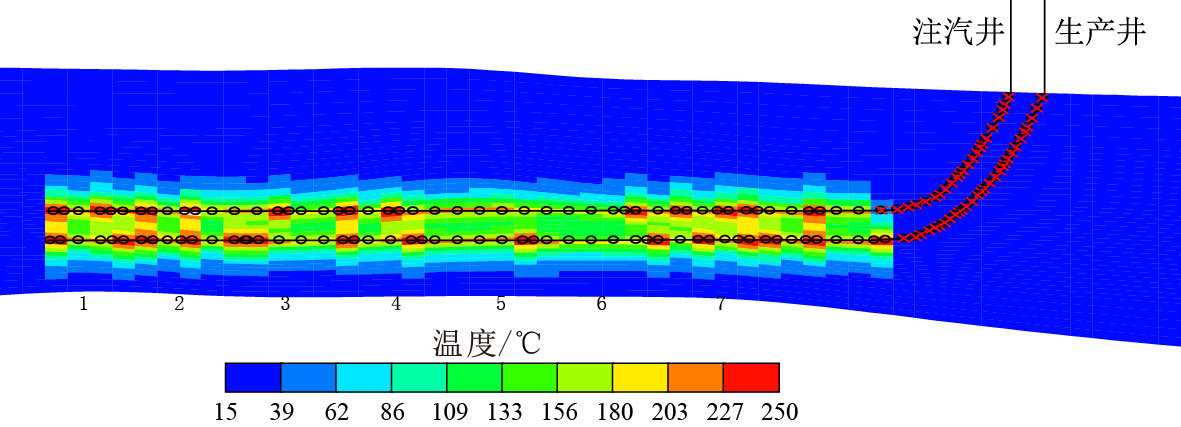 |
| 图2 数值模拟拟合双水平井SAGD循环预热190 d的温度场剖面与测温点分布 Fig. 2 Temperature profile of dual-horizontal well SAGD circulation on 190 d |
新模型解析解与数值模拟计算结果高度吻合(图 3),平均误差不超过2 ℃,表明该解析解具有较高的准确性。
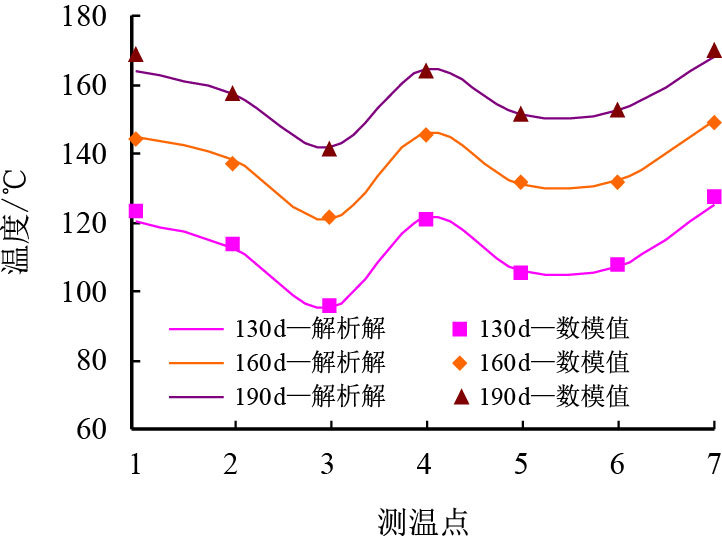 |
| 图3 传热模型解析解与数值模拟结果对比 Fig. 3 Calculation results comparison between new model and numerical simulation model |
由于目前大量新钻完井需要转入循环预热,而由于复杂管柱结构下的SAGD井对模拟计算速度很慢,对所有新完钻的SAGD井对开展数值模拟不现实。因此,利用本文提供的解析模型,对单个井对SAGD循环预热进行了快速跟踪。
3.1 指导优化SAGD生产阶段注汽方式以另一典型SAGD井对FHW1为例,FHW1井对脚尖位置注采井水平段间距离较短,仅为3.6 m,其余位置平均距离5.0 m。从计算结果可见,在SAGD井对脚尖位置出现了优先预热连通,循环预热90 d温度即超过了150 ℃以上(图 4)。由此表明,该井对转SAGD生产以后,将会优先在水平段脚尖处发育蒸汽腔,造成水平段动用不均。为此,推荐转入SAGD生产阶段注汽井采用短油管注汽[14-16],避免水平段脚尖汽窜。
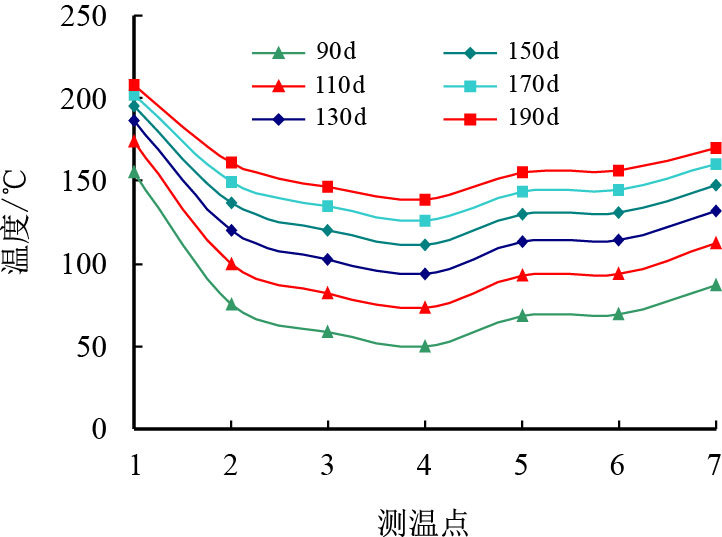 |
| 图4 FHW1井对不同时刻7个测温点温度变化 Fig. 4 Temperature data from 7 points of FHW1 at different time |
以另一试验区典型SAGD井对L2为例,L2井对脚尖位置注采井水平段间距离较为均匀,平均距离5 m,水平段穿过的油层均质性好,孔隙度30%、含油饱和度78%、油层岩性均为砂岩,且热扩散系数较高,平均综合热扩散系数达到0.89$\times$10$^{-6}$~m2/s。利用本文的解析模型,对循环预热不同时刻注采井水平段中间位置的油层升温进行了计算(图 5)。计算结果表明,循环预热130 d注采井水平段中间位置的油层即可升温到130 ℃以上,使该井对应原油黏度下降到100 mPa$\cdot$s以下,表明循环预热130 d即可转入SAGD生产[17]。
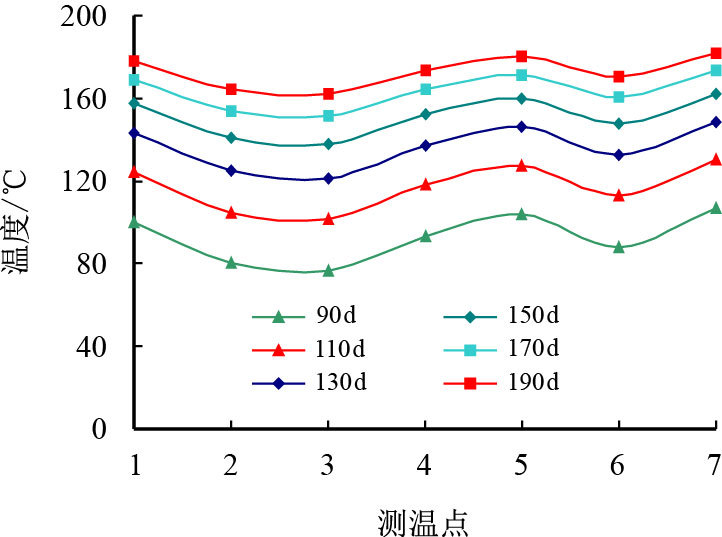 |
| 图5 L2井对不同时刻7个测温点温度变化 Fig. 5 Temperature data from 7 points of L2 at different time |
综合考虑油层传热介质、油层含油饱和度与孔隙度等物性对热扩散能力的综合影响,在前人点源传热叠加解析模型基础上,建立了正确表征SAGD循环预热过程中,热量在油层中的真实传递情况的传热解析新模型。
采用SAGD试验区实际油藏参数与管柱结构参数,建立了表征双水平井SAGD循环预热的油藏数值模拟模型,验证表明,新模型与油藏数值模拟结果高度吻合,具有较高的准确性。
利用新解析模型,对新疆两个SAGD试验区典型井对进行了循环预热跟踪,及时发现了一个井对局部优先预热连通情况,给出了转入SAGD阶段的注汽措施;并给出了另一个SAGD井对结束循环预热转入SAGD的时机。
鉴于该解析模型具有计算速度快,仅需管柱结构参数、油层岩石与油水热物性参数,以及循环预热过程中井下沿程测温数据,即可立即求解出注采井间水平段中间位置油层升温情况等优势,可用于快速判断循环预热井间加热情况,确定转SAGD时机,并指导SAGD生产阶段的操作,对中国开展双水平井SAGD开发的油藏指定合理的操作参数,实现蒸汽腔均匀扩展,具有重要的指导意义。
符号说明
T—温度,℃;
$T_{\rm{i}}$—原始温度,℃;
q—单位长度热流入速度,W/m;
$E_{\rm{i}}$—指数积分函数;
r—距离,m;
$\lambda$—系数,这里$\lambda$ = 8.64$\times$104;W/(m$\cdot$K);
$\alpha$—热扩散系数,m2/s;
t—预热时间,d;
k—导热系数,W/(m$\cdot$K);
$r_{\rm{1}}$—注汽井井筒距x点距离,m;
$r_{\rm{2}}$—生产井井筒距x点距离,m;
d—注汽井与生产井水平段之间距离,m;
$T_x$—x点温度,℃;
$T_{\rm{s1}}$—注汽井循环预热的温度,℃;
$T_{\rm{s2}}$—生产井循环预热的温度,℃;
$q_{\rm{1}}$—热流过注汽井井筒切片的速度,W/m;
$q_{\rm{2}}$—热流过生产井井筒切片的速度,W/m;
$r_{\rm{w1}}$—注汽井井筒半径,m;
$r_{\rm{w2}}$—生产井井筒半径,m;
$r_{\rm{w}}$—注采井井筒半径,m;
$\alpha_{\rm{1}}$—注汽井井筒附近油层岩石基质的热扩散系数,m2/s;
$\alpha_{\rm{2}}$—生产井井筒附近油层岩石基质的热扩散系数,m2/s;
$\alpha_{}$—注采井筒附近油层岩石基质的热扩散系数,m2/s;
$t_{\rm{1}}$—注汽井预热时间,d;
$t_{\rm{2}}$—生产井预热时间,d;
$k_{\rm{1}}$—注汽井井筒附近油层岩石导热系数,W/(m$\cdot$K);
$k_{\rm{2}}$—生产井井筒附近油层岩石导热系数,W/(m$\cdot$K);
${\alpha _{{\rm{mix}}}}$—综合热扩散系数,m2/s;
${\lambda _{{\rm{mix}}}}$—油层综合导热系数,W/(m$\cdot$K);
${\lambda _{\rm{f}}}$—岩石基质导热系数,W/(m$\cdot$K);
${\phi _{\rm{f}}}$—油层孔隙度,%;
${\lambda _{\rm{w}}}$—地层水导热系数;
${\lambda _{\rm{o}}}$—地层原油导热系数;
${S_{\rm{w}}}$—含水饱和度,%;
${S_{\rm{o}}}$—含油饱和度,%;
${\rho_{\rm{mix}}}$—综合密度,g/cm3;
${\rho_{\rm{f}}}$—岩石基质密度,g/cm3;
${\rho_{\rm{o}}}$—原油密度,g/cm3;
${\rho_{\rm{w}}}$—地层水的密度,g/cm3;
${f_{\rm{gr}}}$—岩石基质的质量分数,%;
${f_{\rm{o}}}$—原油的质量分数,%;
${f_{\rm{w}}}$—地层水的质量分数,%;
${C_{\rm{mix}}}$—综合比热容,J/(g$\cdot$℃);
${C_{\rm{f}}}$—岩石基质的比热容,J/(g$\cdot$℃);
${C_{\rm{o}}}$—原油的比热容,J/(g$\cdot$℃);
${C_{\rm{w}}}$—地层水的比热容,J/(g$\cdot$℃)。
| [1] | NUKHAEV M, PIMENOV V, SHANDRYGIN A, et al. Near-wellbore formation evaluation via distributed temperature data[C]//Canadian International Petroleum Conference. Petroleum Society of Canada, 2006. |
| [2] | NASR T N, LAW D H S, GOLBECK H, et al. Countercurrent aspect of the SAGD process[J]. Journal of Canadian Petroleum Technology, 2000, 39 (1) : 41 –47. |
| [3] | VINCENT K D, MACKINNON C J, PALMGREN C T S. Developing SAGD operating strategy using a coupled wellbore thermal reservoir simulator[C]. SPE 86970, 2004. http://cn.bing.com/academic/profile?id=2004013211&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] | PARMAR G, ZHAO L, GRAHAM J. Start-up of SAGD wells:history match, wellbore design and operation[J]. Journal of Canadian Petroleum Technology, 2009, 48 (1) : 42 –48. DOI:10.2118/09-01-42 |
| [5] | MIURA K, WANG J. An analytical model to predict cumulative steam/oil ratio(CSOR) in thermal-recovery SAGD process[J]. Journal of Canadian Petroleum Technology, 2012, 51 (4) : 268 –275. DOI:10.2118/137604-PA |
| [6] | DUONG A N, TOMBERLIN T, CYROT M. A New analytical Model for Conduction heating during the SAGD Circulation Phase[C]. SPE/PS/CHOA 117434, 2008. |
| [7] | 纪佑军, 程林松, 刘志波, 等. SAGD过程注氮气改善开发效果实验研究[J]. 西南石油大学学报(自然科学版), 2010, 32 (2) : 108 –112. |
| [8] |
张小波, 郑学男, 邰德军, 等. SAGD添加非凝析气技术研究[J].
西南石油大学学报(自然科学版), 2010, 32 (2) : 113 –117.
ZHANG Xiaobo, ZHENG Xuenan, TAI Dejun, et al. The technical research on adding none condensate gas in SAGD[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2010, 32 (2) : 113 –117. |
| [9] |
席长丰, 马德胜, 李秀峦. 双水平井超稠油SAGD循环预热启动优化研究[J].
西南石油大学学报(自然科学版), 2010, 32 (4) : 103 –108.
XI Changfeng, MA Desheng, LI Xiuluan. Study on SAGD tecnology for ultra heavy oil in dual horizontal wells[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2010, 32 (4) : 103 –108. |
| [10] | 肖娟. 超稠油油藏双水平井SAGD循环预热优化设计研究[J]. 特种油气藏, 2010, 17 (增) : 119 –121. |
| [11] |
陈森, 窦升军, 游红娟, 等. 风城SAGD水平井均匀配汽工艺研究与应用[J].
石油钻采工艺, 2012, 34 (2) : 114 –116.
CHEN Sen, DOU Shengjun, YOU Hongjuan, et al. Research and application of uniform steam injection in SAGD horizontal wells of Feng city oilfield[J]. Oil Drilling & Production Technology, 2012, 34 (2) : 114 –116. |
| [12] |
刘敏, 高孝田, 邹剑, 等. 海上特稠油热采SAGD技术方案设计[J].
石油钻采工艺, 2013, 35 (4) : 94 –96.
LIU Min, GAO Xiatian, ZOU Jian, et al. SAGD technology conceptual design of thermal recovery explore for offshore extra-heavy oil[J]. Oil Drilling & Production Technology, 2013, 35 (4) : 94 –96. |
| [13] |
罗晓琴, 杨振萍, 陈昭栋. 热线法测量材料的热扩散系数和热导率的研究[J].
四川师范大学学报(自然科学版), 2013, 36 (5) : 792 –794.
LUO Xiaoqin, YANG Zhenping, CHEN Zhaodong. Investigation on transient measurent of thermal conductivity and thermal diffusion by thermal line method[J]. Journal of Sichuan Normal University(Natural Science), 2013, 36 (5) : 792 –794. |
| [14] |
陈森, 窦升军, 游红娟, 等. 双水平井SAGD循环预热技术及现场应用[J].
新疆石油天然气, 2012, 8 (S) : 6 –10.
CHEN Sen, DOU Shengjun, YOU Hongjuan, et al. Application of SAGD recycle preheating technology to bilateral horizontal well[J]. Xinjiang Oil & Gas, 2012, 8 (S) : 6 –10. |
| [15] | 刘名, 邓琴, 杨文学, 等. 双水平井SAGD循环预热阶段调控及认识[J]. 新疆石油天然气, 2011, 7 (3) : 38 –41. |
| [16] |
马德胜, 郭嘉, 昝成, 等. 蒸汽辅助重力泄油改善汽腔发育均匀性物理模拟[J].
石油勘探与开发, 2013, 40 (2) : 188 –193.
MA Desheng, GUO Jia, ZAN Cheng, et al. Physical simulation of improving the uniformity of steam chamber growth in the steam assisted gravity drainage[J]. Petroleum Exploration and Development, 2013, 40 (2) : 188 –193. |
| [17] |
霍进, 桑林翔, 杨果, 等. 蒸汽辅助重力泄油循环预热阶段优化控制技术[J].
新疆石油地质, 2013, 34 (4) : 455 –457.
HUO Jin, SANG Linxiang, YANG Guo, et al. Optimization and control techniques for circulating preheating stage by steam assisted gravity drainage(SNGD) process[J]. Xinjiang Petroleum Geology, 2013, 34 (4) : 455 –457. |
 2016, Vol. 38
2016, Vol. 38


